3. IQサンプリング¶

この章では、IQサンプリング(IQ sampling)の考え方を紹介します。 IQサンプリングは、複素サンプリング(complex sampling)または直交サンプリング(quadrature sampling)とも呼ばれます。また、ナイキストサンプリング、複素数、RFキャリア、ダウンコンバージョン、そしてパワースペクトル密度についても取り上げます。 IQサンプリングは、SDRや多くのデジタル送受信機が用いるサンプリング方法です。複素数(complex number)なだけに、これは通常のデジタルサンプリングよりも少し複雑(complex)ですので時間をかけて説明しますし、練習すれば必ず全て理解できるようになります！

サンプリングの基礎¶

IQサンプリングの話に入る前に、そもそもサンプリングが何を意味するのか考えてみましょう。マイクで音声を録音したことがあれば、あなたは知らず知らずのうちにサンプリングを経験しています。マイクは音波を電気信号(電圧)に変換する変換器(transducer)です。この電気信号は、アナログ-デジタルコンバータ(Analog-to-Digital Converter、ADC)によってデジタル化された音波に変換されます。簡単に言えば、マイクが音波を拾い、それが電気信号になり、さらにその電気が数字に変換されるということです。 ADCはアナログ領域とディジタル領域の間の橋渡しとなります。 SDRもこれと驚くほど似ています。 SDRはマイクの代わりにアンテナを使いますが、SDRもADCを使用しています。どちらの場合も電圧レベルがADCでサンプリングされるのです。 SDRでは電波が入力され、数字が出力されます。

音声であれ無線周波数であれ、信号をデジタルで取得・処理・保存したいのであれば、サンプリングを行う必要があります。サンプリングは一見単純に思えるかもしれませんが、実際のところ複雑です。より技術的に言うと、信号のサンプリングとは各時間における値を取得してデジタルで保存することです。例えば、以下の任意の連続関数 $S(t)$ のサンプリングをしたい場合を考えます。

信号のサンプリングの考え方。サンプリング周期はTで、サンプルを青い点で示している。

$S(t)$ の値を $T$ 秒ごとの一定間隔、すなわち サンプリング周期(sampling period) で記録します。サンプリングする頻度、つまり1秒あたりに取得するサンプルの数は当然 $\frac{1}{T}$ です。これを サンプルレート(sample rate) と呼び、サンプリング周期の逆数となります。例えば、サンプルレートが10 Hzであればサンプリング周期は0.1秒となり、各サンプルの間には0.1秒の間隔があることになります。実際のサンプルレートは数百kHzから数十MHz、あるいはそれ以上になることもあります。信号をサンプリングする際には、サンプルレートを慎重に設定する必要があります。サンプルレートは非常に重要なパラメータです。

数学的な表現を好む人のためにも数式を用いて説明します。 $S_n$ を $n$ とし、 $n$ は通常、0以上の整数となります。この記法を用いると、整数 $n$ に対してサンプリングの過程は数学的に $S_n = S(nT)$ と表現することができます。つまり、アナログ信号 $S(t)$ を $nT$ の間隔ごとに評価(測定)しているということです。

ナイキストサンプリング¶

ある信号が与えられた時にしばしば重要な問題となるのが、どれくらい速くサンプリングするべきかということです。下図の緑で示された周波数fの単純な正弦波を例に考えてみましょう。例えばこの信号をサンプリングレートFsでサンプリングするとします(青でサンプルが示されています)。もしサンプリングレートが信号の周波数fと等しい(Fs=f)場合、次のような結果が得られます。

上の画像の赤い破線は、サンプルから再構成したオリジナルとは異なる(すなわち誤った)関数です。しかし、実際にはサンプルはこの関数から得られたものだったかもしれません。ここから分かることは、サンプリングレートが十分ではなかったということです。なぜなら、同じサンプルを取りうる2つの異なる関数が存在し、関数を一意に決定できないからです。元の信号を正確に再構成するためには、このような曖昧さは許されません。

Fs = 1.2fにして、もう少し速くサンプリングしてみましょう。

またしても、これらのサンプルに合致する別の信号が存在し得ます。このように関数を一意に決められないということは、誰かがこのサンプルのリストを私たちに渡したとしても、元の信号がどの信号だったのかをサンプリング結果だけでは区別できないということです。

Fs = 1.5f ではどうでしょうか?

ナイキストレートを下回る速度で信号をサンプリングした場合に生じるサンプリングの曖昧さの例

まだ十分速くありません！詳しくは触れませんが、DSPの理論によると現在私たちが直面している曖昧さを解決するためには、信号の 2倍の周波数でサンプリングする必要があります。

今回は誤った信号は存在しません。サンプリング速度が十分に速かったため、これらのサンプルに合致する信号は今見えているもの以外に存在しません( より高い 周波数の信号を除けばですが、それについては後ほど説明します)。

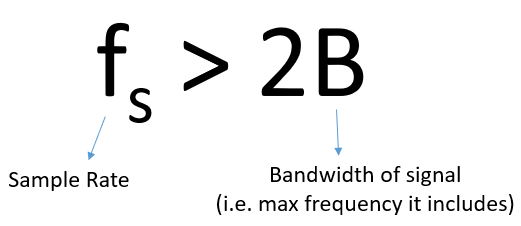
上の例での信号は単純な正弦波でしたが、実際の信号にはたいてい複数の周波数成分が含まれています。任意の信号を正確にサンプリングするには、「最大周波数成分の2倍以上のサンプリングレート」が必要です。以下は周波数領域のプロット例です。なお、常にノイズフロアが存在するため、通常は最高周波数を近似することになります。

ナイキストサンプリングとは、サンプリングレートが信号の最大帯域幅よりも高いことを意味します。

私たちはまず、信号の中で最も高い周波数成分を特定し、その2倍以上の速度でサンプリングする必要があります。この最小のサンプリングレートはナイキストレート(Nyquist Rate)と呼ばれます。言い換えれば、ナイキストレートとは、(有限の帯域幅を持つ)信号のすべての情報を保持するために必要な最小のサンプリングレートです。これは、DSPやSDRにおける非常に重要な理論であり、連続信号と離散信号の橋渡しとなります。

十分な速度でサンプリングしないとエイリアシングと呼ばれる現象が発生します。エイリアシングは後で学びますが、これは何としてでも避けるべきものです。 SDR(および一般的な受信機)は、サンプリングの直前にFs/2を超える周波数成分をすべてフィルタで除去します。サンプリングレートが低すぎると、フィルタが信号の一部を切り捨ててしまいます。 SDRには、エイリアシングやその他の欠陥のないサンプルを提供するための多くの工夫が施されています。 SDRのアンチエイリアシングフィルタは、通過帯域(passband)から阻止帯域(stopband)に瞬時に切り替わるわけではないため(つまり、わずかな遷移帯域(transition band)が必要なため)、経験則に基づいてサンプルレートの中央の4/5を使用可能だとみなします。これを「ショーンの4/5ルール(Sean’s 4/5 rule)」と呼びます。

直交サンプリング¶

「直交(quadrature)」という言葉には多くの意味がありますが、DSPやSDRの文脈では位相が90度ずれた2つの波を指します。なぜ90度の位相差なのでしょうか? 180度ずれた2つの波は、一方に-1をかけると本質的に同じ波になることが分かります。 90度ずれると、2つの波は互いに直交(orthogonal)になり、直交な関数を使って様々な面白いことを実現することができます。簡単のために、90度ずれた2つの正弦波として、sin波とcos波を使います。

次に、cos波とsin波の振幅を表す変数を割り当てましょう。 cos() の振幅を $I$ 、sin() の振幅を $Q$ とします。

$I \cos(2\pi ft) Q \sin(2\pi ft)$

IとQがそれぞれ1の時のプロットは以下のようになります。

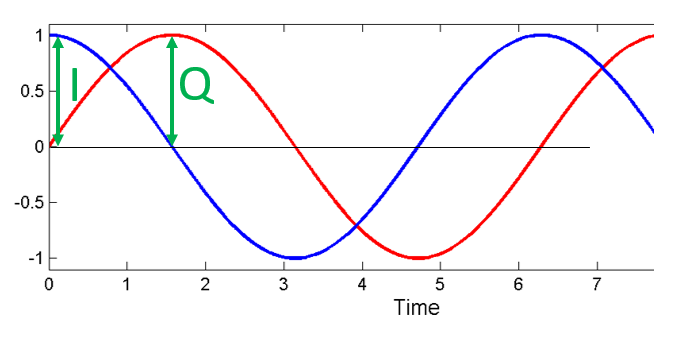
cos() を「同相成分(in phase)」と呼び、Iと表します。そして、sin()は90度位相がずれており「直交(quadrature)」しているため、Qと表します。ただし、もし間違えてQをcos()に、Iをsin()に割り当てたとしても、ほとんどの場面では問題ありません。

IQサンプリングをより直感的に理解するには、送信側の視点、つまり、RF信号を空中に送信する作業から考えると分かりやすくなります。特定の位相を持つ正弦波を送信するには、位相0のsin()とcos()の和を送信すれば良いです。これは三角関数の恒等式(三角関数の合成公式) $a \cos(x) + b \sin(x) = A \cos(x-\phi)$ が成立するためです。送信したい信号をx(t)としましょう。

$x(t) = I \cos(2\pi ft) + Q \sin(2\pi ft)$

sinとcosを足し合わせるとどうなるでしょうか? より厳密に言えば、90度位相がずれた2つの正弦波を足し合わせるとどうなるでしょうか? 以下の動画には、IとQを調整するスライダーがあります。プロットされているのは、cos、sin、そして2つの和です。

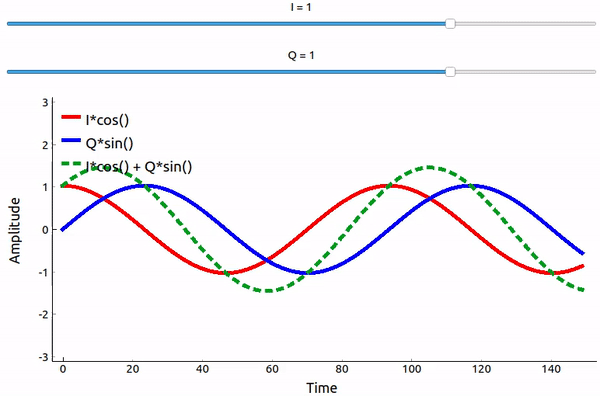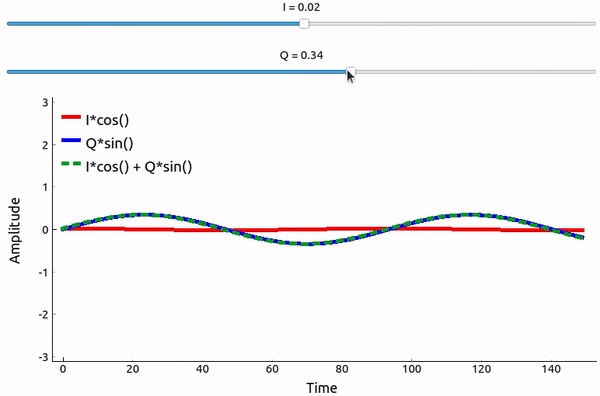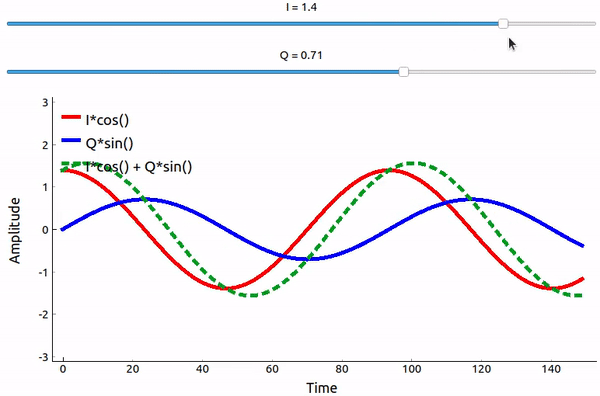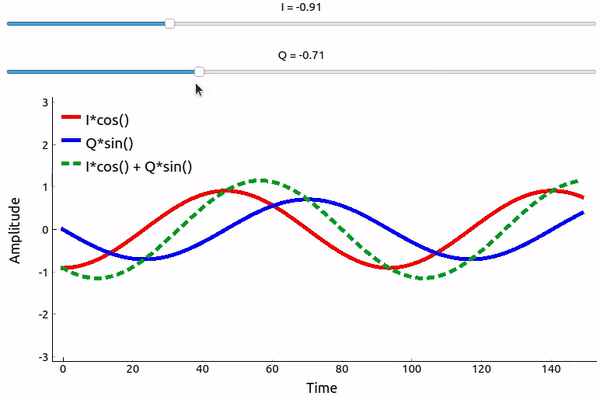
IとQを正弦波の振幅とし、合成される正弦波をGNU Radioで示したアニメーション

(このアプリで使われている pyqtgraph ベースの Python コードは here にあります)

重要なポイントは、cos() と sin() を足し合わせると振幅と位相が異なる純粋な正弦波が得られるということです。また、片方の成分を徐々に減らしたり加えたりすると位相がシフトします。さらに、振幅も変化します。これはすべて、三角関数の恒等式( $a \cos(x) + b \sin(x) = A \cos(x-\phi)$ )に基づくものです。この式には後ほど再び触れます。この性質を使うと、IとQの振幅を調整するだけで出力の正弦波の位相と振幅をコントロールできるため「有益」です(cos波あるいはsin波の位相を調整する必要はありません)。例えばIとQを調整することで、振幅を一定に保ったまま位相だけ任意の値に変更することもできます。送信機にとって、これができることは非常に重要です。なぜなら、電磁波として空中に伝搬させるためには正弦波信号を送信する必要があるからです。そして、位相と振幅を調整するよりも、IとQという2つの振幅を調整して加算する方がはるかに簡単なのです。結果として、送信機の構成は次のようになります。

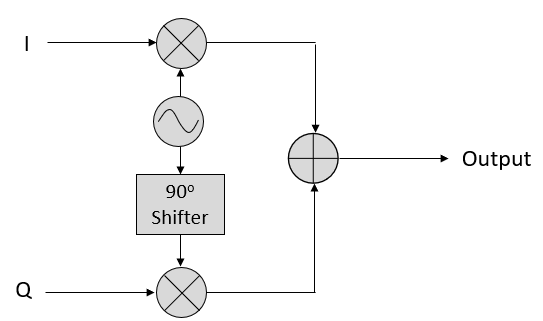
1つの正弦波を生成して位相を90度シフトするだけでQ成分を得ることができます。

複素数¶

本質的には、IQは振幅と位相を別の方法で表現したものであり、複素数および複素平面による表現を用いて理解を深めることができます。他の授業で複素数を見たことがあるかもしれません。複素数0.7-0.4jを例にとって考えてみましょう。

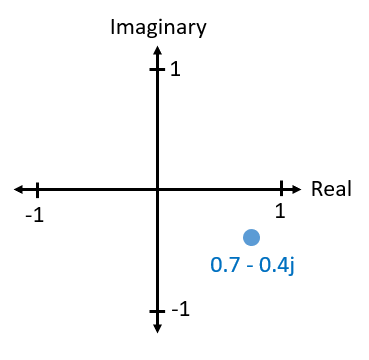
複素数とは、実部(real)と虚部(imaginary)という2つの数値を組み合わせただけのものです。複素数には振幅と位相があり、点ではなくベクトルとして考えると理解しやすくなります。振幅は原点とその点を結ぶ線分の長さ(ベクトルの大きさ)であり、位相はそのベクトルと0度方向(正の実軸)の間の角度です。

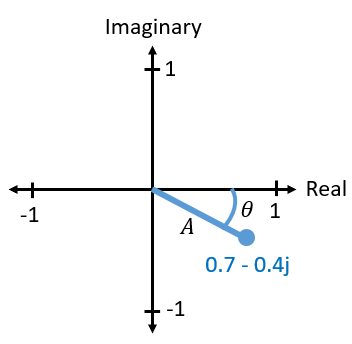
このような正弦波の表現は「フェーザ図(phasor diagram)」として知られています。これは単に複素数をプロットしてベクトルして扱う方法です。では、例として挙げた複素数0.7-0.4jの振幅と位相はなんでしょうか? 与えられた複素数の実部を $a$ 、虚部を $b$ としたとき、以下のように求めることができます。

$\mathrm{magnitude} = \sqrt{a^2 + b^2} = 0.806 \mathrm{phase} = \tan^{-1} \left( \frac{b}{a} \right) = -29.7^{\circ} = -0.519 \quad \mathrm{radians}$

Pythonでは、振幅と位相を求めるのにnp.abs(x)とnp.angle(x)が使えます。入力は複素数または複素数の配列で、出力は実数または実数の配列(float型)です。

ベクトルまたはフェーザ図とIQ表現の間の関係について既にお気づきかもしれません。 I が実部、Q が虚部に対応します。以降で複素平面を描くときは、実部と虚部の代わりにIとQを軸ラベルとして使用します。これらは依然として複素数です！

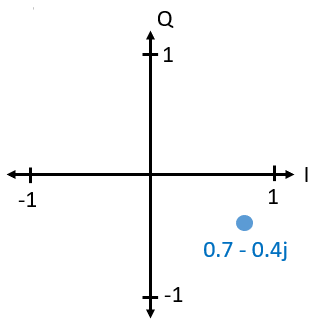
例えば点 0.7-0.4jを送信したいとします。このとき以下を送信することになります。

$x(t) = I \cos(2\pi ft) + Q \sin(2\pi ft) \quad \quad \quad = 0.7 \cos(2\pi ft) - 0.4 \sin(2\pi ft)$

振幅を $A$ 、位相を $\phi$ として三角関数の恒等式 $a \cos(x) + b \sin(x) = A \cos(x-\phi)$ を使うと、振幅は $\sqrt{I^2 + Q^2}$ 、位相は $\tan^{-1} \left( Q/I \right)$ となります。従って、上の式は以下のようになります。

$x(t) = 0.806 \cos(2\pi ft + 0.519)$

最初は複素数から始めましたが、送信するのはある振幅と位相を持った実数信号です。虚数を実際に電磁波で送信することはできません。私たちは送信する情報の表現する方法としてのみ虚数・複素数を使っています。 $f$ については、このあとすぐに説明します。

FFTにおける複素数¶

上記で扱った複素数は時間領域のサンプルであると仮定していましたが、FFTを行うときにも複素数が登場します。前章でフーリエ級数やFFTについて学んだ際には、まだ複素数について詳しく扱っていませんでした。サンプルにFFTを適用すると、周波数領域での値が得られます。 FFTがサンプルに存在する周波数成分を計算する方法については既に説明しました(FFTの振幅は各周波数の強さを示しています)。しかし、FFTはさらに、正弦波を足し合わせて時間領域の信号を再構成するのに必要な遅延(時間シフト)も計算しています。この遅延がFFTの位相です。 FFTの出力は複素数の配列であり、各複素数は振幅と位相を持ち、配列のインデックスが周波数を表します。その周波数・振幅・位相をもつ正弦波を生成して足し合わせれば、元の時間領域の信号が得られます(あるいはそれにとても近い信号が得られ、これはナイキストの標本化定理と関係しています)。

受信機¶

それでは、信号(例えばFM無線信号)を受信しようとしている無線受信機の視点で考えてみましょう。 IQサンプリングを使う場合、ブロック図は以下のようになります。

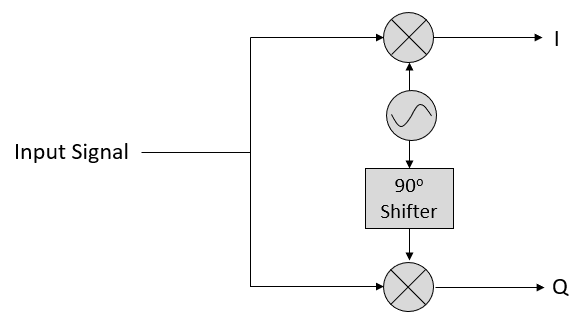
入力信号に正弦波と、その90度位相がずれた正弦波を直接乗算してIQサンプルを取得する

アンテナで受信した実数信号が入力となり、これはIQ値に変換されます。つまり、2つのADCを使ってIとQの枝分かれのサンプリングをそれぞれ行い、各ペアを複素数として保存します。言い換えれば、各タイムステップでIとQの値を1つずつサンプリングし、 $I + jQ$ にします(つまり1つのIQサンプリングで1つの複素数が得られます)。サンプリングする時には、サンプリングするレートである「サンプルレート(sample rate)」が常に関係します。例えば「2 MHz のサンプルレートで SDR を動かしている」人がいた場合、それは毎秒200万のIQサンプルをSDRが受信しているという意味になります。

誰かに大量のIQサンプルをもらうと、それは複素数の1次元配列(ベクトル)になっているでしょう。複雑だったかもしれませんが、このポイントこそがこの章全体で目指してきた核心であり、ついにここまで辿り着きました。

この教材を通じてIQ サンプルの仕組み、SDR を使った送受信方法、Pythonによるそれらの処理方法、そして解析用にファイルを保存する方法が とても よく分かるようになります。

最後に重要な注意点を示します。上の図は SDRの内部で起こっていることを示しています。正弦波の生成や90度の位相シフト、掛け算や加算などを実際に自分で行う必要はありません。これらはSDRがやってくれます。私たちはSDRにどの周波数をサンプリングしたいのか、あるいはどの周波数で送信したいのかを伝えます。受信する場合、SDRはIQサンプルを出力してくれます。送信する場合、私たちがSDRにIQサンプルを与える必要があります。データ型は、複素整数または複素浮動小数点が使われます。

搬送波とダウンコンバージョン¶

ここまで周波数については触れてきませんでしたが、cos()やsin()を含む式の中には $f$ が出てくることを既に学びました。この周波数は、実際に空中に送信する信号の中心周波数(center frequency)、つまり電磁波の周波数です。これは、ある無線周波数で信号を運ぶ役割を果たしているため、搬送波(carrier)と呼ばれます。 SDRの周波数をチューニングしてサンプルを受信すると、情報はIとQに保存されます。搬送波の周波数にチューニングしていれば、IとQに搬送波は含まれません。

Figure made with TikZ

参考までに、FMラジオ、WiFi、Bluetooth、LTE、GPS などの無線信号は、通常100 MHzから6 GHzの範囲の周波数(つまり搬送波)を使用します。これらの周波数は空中を良好に伝搬する一方で、非常に長いアンテナは不要かつ送受信時に大量の電力を必要としません。電子レンジは2.4 GHzの電磁波で食品を加熱します。もし扉から電磁波が漏れると、電子レンジはWiFi信号を妨害し、さらには皮膚を火傷させるかもしれません。光も電磁波の一種です。可視光の周波数は約500 THzです。周波数が高いため、光を送信するのに通常のアンテナは使用されません。 LEDのような半導体デバイスを用いた方法が使用されます。半導体デバイスでは、半導体材料(semiconductor material)の原子軌道に電子が入り込んだ時に光が生じます。その時の色は、電子がジャンプした距離によって決まります。法律上、無線周波数(Radio Frequency、RF)は約20 kHzから300 GHzの範囲と定義されています。これは、交流電流のエネルギーが導体(アンテナ)から放射し空間を伝搬できる周波数です。少なくとも近年のほとんどの用途では、100 MHzから6 GHzが実用的な周波数です。 6 GHz を超える周波数は、長年にわたってレーダーや衛星通信に使われてきましたが、現在では 5Gの「ミリ波(mmWage)」(24-29 GHz)でも使用され、低周波帯を補完し通信速度を向上させています。

IQ値を高速に変化させて搬送波を送信することを、(データか何かで)搬送波を変調する(modulate)といいます。 IとQを変化させるということは、搬送波の位相と振幅を変化させるということになります。別の方法として、搬送波の周波数自体をわずかに上下させる方法もあります。これはFMラジオで使われている方式です。

簡単な例として、IQサンプル1+0jを送信したあと0+1jを送信する場合を考えます。この場合、搬送波は $\cos(2\pi ft)$ から $\sin(2\pi ft)$ へと変化し、サンプルを切り替えると位相が90度シフトすることになります。

送信したい信号(一般に複数の周波数成分を含みます)と、それを送信する周波数(搬送波周波数)は混同されがちです。ベースバンド信号とバンドパス信号を扱う時に、これらの違いは明確になるでしょう。

ここで少しの間、サンプリングに話を戻します。アンテナからの信号に cos() と sin() を掛けてIとQを記録する代わりに、アンテナからの信号をそのまま1つのADCに入力したらどうなるでしょう? 例えば、搬送波周波数がWiFiやBluetoothと同様に2.4GHzだとします。以前学んだように、この時には4.8 GHzでサンプリングする必要があります。これは非常に高速です！そんな速度でサンプリングできるADCは数千ドルもします。そこで、信号をダウンコンバート(downconvert)し、サンプリングしたい信号の中心が直流(DC)、つまり0 Hzに来るように周波数を下げます。このダウンコンバージョンの処理はサンプリングの前に行われます。

以下のようにIとQだけの式を考えます。

$I \cos(2\pi ft) Q \sin(2\pi ft)$

ダウンコンバージョンを周波数領域で可視化してみましょう。

信号の周波数をRFから0 Hzあるいはベースバンドにシフトするダウンコンバージョン処理

0 Hzを中心にした場合、搬送波が取り除かれたことにより最大周波数は2.4 GHzではなく信号の性質に基づいた値になります。ほとんどの信号の帯域幅は約100 kHzから40 MHz程度なので、ダウンコンバージョンによって はるかに 低いレートでサンプリングすることが可能になります。 B2X0 USRPとPlutoSDRは、最大56 MHzまでサンプリング可能な無線周波数集積回路(Radio Frequency Integrated Circuit, RFIC)が搭載されており、これは私たちが扱うほとんどの信号にとって十分な性能です。

繰り返しになりますが、ダウンコンバージョンの処理は SDRによって自動的に行われます。 SDRを使うユーザーはどの周波数にチューニングするかを指定するだけでよく、それ以外の操作は不要です。ダウンコンバージョン(およびアップコンバージョン)はミキサー(mixer)と呼ばれる部品によって行われ、図では通常、円の中に描かれた掛け算記号で表されます。ミキサーは入力信号を受けてダウン・アップコンバウジョンされた信号を出力します。また、3番目のポートを持ち、発振器(oscillator)の信号が入力されます。信号に適用される周波数シフトはこの発振器の周波数によって決まります。ミキサーの本質は単なる乗算関数です(正弦波を掛けることで周波数がシフトするということを思い出してください)。

最後に、信号が空中を伝わる速度に興味を持たれるかもしれません。高校の物理で習ったとおり、無線機は低周波(約3 kHzから80 GHz)の電磁波を使用します。可視光も電磁波ですが、周波数ははるかに高くなります(約400 THzから700 THz)。空気中(真空中)では、全ての電磁波は光速(約 3e8 m/s)で伝搬します。電磁波は常に同じ速度で伝わるため、1 回の振動(正弦波の1周期)で進む距離はその周波数によって決まります。この距離を波長と呼び、 $\lambda$ で表します。以下の関係式を見たことがあると思います。

$f = \frac{c}{\lambda}$

ここで $c$ は光の速度であり、 $f$ をHz、 $\lambda$ をメートル単位で表す場合、3e8に通常は設定されます。無線通信では、この関係はアンテナの話になると重要になります。というのも、ある搬送波周波数 $f$ の信号を受信するには、その波長 $\lambda$ に対応したアンテナ(たいていは $\lambda/2$ または $\lambda/4$ の長さのアンテナ)が必要だからです。ただし、周波数や波長にかかわらず、その信号にのった情報は常に送信機から受信機へ光速で伝わります。この時の空中を伝わる遅延を見積もる方法として、光が1ナノ秒で約1フィート(30cm)進むという考えを利用することができます。また、静止軌道上の衛星との往復にかかる時間は約0.25秒程度です。

受信機のアーキテクチャ¶

「受信機」のセクションにある図は、入力信号がダウンコンバートされてIとQに分離される様子を示しています。この構成はRF周波数をベースバンドまで直接落としているため、「ダイレクトコンバージョン(direct conversion)」または「ゼロIF(zero IF)」と呼ばれます。他の選択肢として、ダウンコンバージョンを全く行わずに、0 Hzからサンプリング周波数の1/2までを高速にサンプリングする方法があります。この方式は「ダイレクトサンプリング(direct sampling)」または「ダイレクトRF(direct RF)」と呼ばれ、非常に高価なADCチップを必要とします。 3つ目のアーキテクチャは「スーパーへテロダイン(superheterodyne)」と呼ばれ、これは古い無線機で使用されていたため有名です。これもダウンコーバージョンを行いますが、0Hzまでは変換しません。代わりに、目的の信号を「中間周波数(Intermediate Frequency、IF)」と呼ばれる周波数に移動させます。「低雑音増幅器(LNA: Low Noise Amplifier)」は、入力される非常に微弱な信号を増幅するために設計されたアンプです。以下に、これら3つの代表的な受信機のアーキテクチャのブロック図を示しますが、さまざまな派生が存在することに注意してください。

代表的な3つの受信機アーキテクチャ:ダイレクトサンプリング、ダイレクトコンバージョン、スーパーへテロダイン

ベースバンド信号とバンドパス信号¶

0 Hzを中心とする信号は「ベースバンド(baseband)」にあると言います。これに対して0 Hzから離れたRF周波数に存在し、無線伝送のために上方に周波数シフトされた信号は「バンドパス(bandpass)」と呼ばれます。虚数を実際に送信することはできないため、「ベースバンド伝送(baseband transmission)」という概念は存在しません。ベースバンドの信号は、搬送波とダウンコンバージョンの章の右側の図のように0 Hzを正確に中心に持つ場合もあります。また、以下に示す2つの信号のように、0 Hz の 近傍に 存在することもありえます。これらの信号も依然としてベースバンド信号とみなされます。また、図には中心周波数 $f_c$ にある高い周波数のバンドパス信号の例も示されています。

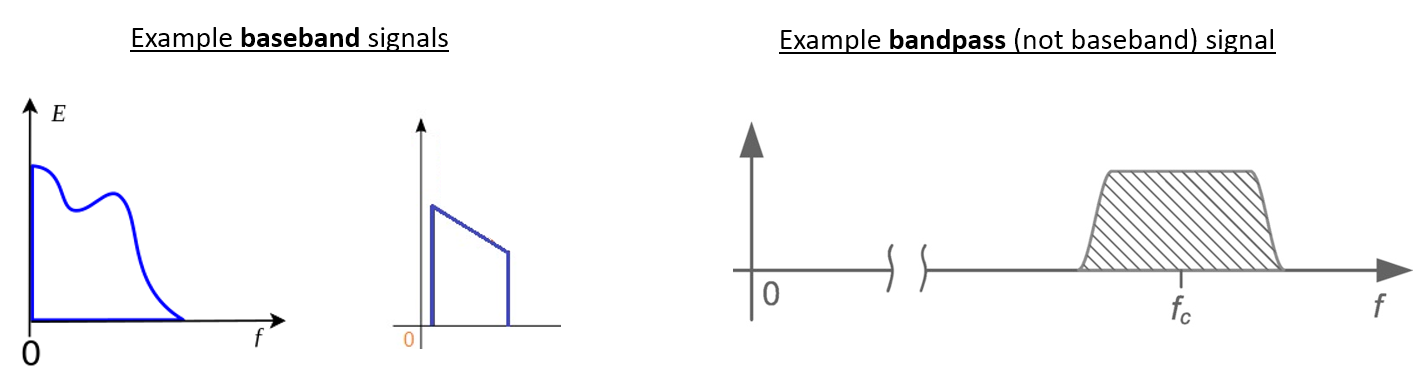
「中間周波数(Intermediate Frequency、IF)」という用語も耳にするかもしれません。これはベースバンドとバンドパス/RFの間に位置する、受信機内の中間的な周波数変換のステップを指します。

低いサンプルレートで扱えるようにするために、信号の生成、記録、解析はベースバンドで行われることが一般的です(その理由は前節で説明した通りです)。ここで重要な点は、ベースバンド信号は複素信号であり、バンドパス信号(例えば実際にRFで送信する信号)は実数であるということです。複素・虚数信号を直接送信することはできないため、アンテナから出力する信号はすべて実数でなければなりません。信号の正の周波数成分と負の周波数成分が完全に一致していない場合、その信号は複素信号であるとわかります。複素数を使うことで負の周波数という概念を表現できます。現実には負の周波数が存在せず、これは単に搬送波周波数を下回る成分にすぎません。

信号に虚数成分が全く含まれない場合、それはQ値を持たない(またはすべてのQ値がゼロである)ことを意味します。この場合、位相シフトのない余弦波(コサイン波)のみで構成されていることになります。位相シフトを持たない余弦波の和を周波数領域でプロットすると、正負の成分が同じためy軸対称となります。

前のセクションで扱った複素点0.7-0.4jは、ベースバンド信号における1サンプルを表現していました。複素サンプル(IQサンプル)はほぼ全てベースバンド領域で示されています。 RF信号がデジタルで表現あるいは保存されることは滅多にありません。なぜなら、膨大なデータ量が必要になり、また、私たちが通常関心を持っているのはRFスペクトルのごく一部だからです。

DCスパイクとオフセットチューニング¶

SDRを扱い始めると、FFTの中心に大きなスパイクが現れることがよくあります。これは「DCオフセット(DC offset)」や「DCスパイク(DC spike)」、あるいは「LOリーケージ(Local Oscillator leakage)」と呼ばれます。

以下はDCスパイクの例です。

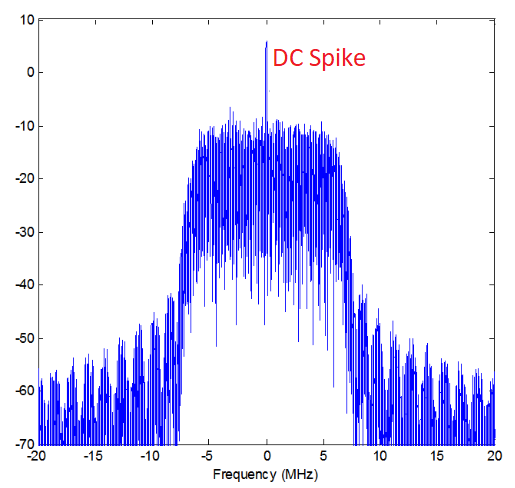
SDRは中心周波数にチューニングされているため、FFTの0 Hzの位置がその中心周波数に対応しています。したがって、DCスパイクがあるからといって、必ずしも中心周波数にエネルギーがあるわけではありません。もしFFTの中央にDCスパイクだけが現れており、他の部分がノイズのように見える場合、そこに本物の信号は存在しない可能性が高いです。

DCオフセットは、PlutoSDR、RTL-SDR、LimeSDR、その他多くのEttus USRPといったSDRで使われているダイレクトコンバージョン受信機アーキテクチャにおける一般的な副作用です。ダイレクトコンバージョン受信機では、発振器、すなわちLOが受信信号をベースバンドに直接ダウンコンバートします。その際、LO自体からのリーケージ(leakage)が観測帯域の中央に現れるのです。 LOリーケージ(LO leakage)とは、異なる周波数が混ざり合って発生する余分なエネルギーのことを指します。目的の信号と非常に近い周波数に現れるため、この余計なノイズを除去するのは難しいです。多くのRF集積回路(RFIC)には自動的にDCオフセットを除去する機能が備わっていますが、これは信号が存在する状態でないと動作しない場合がほとんどです。従って、信号がまったくない時にはDCスパイクが顕著に見えてしまいます。

DCオフセットを手早く処理する方法は、オーバーサンプリングしてチューニング周波数をずらすこと(off-tune)です。これを一般に オフセットチューニング(offset tuning) と呼びます。例えば5 MHzのスペクトルを100 MHzで観測したいとします。この時、代わりに中心周波数を95 MHzに設定し、20 MHzでサンプリングします。

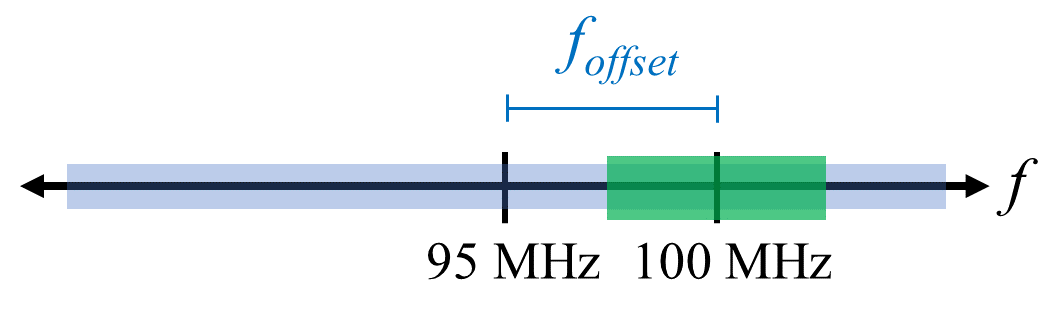
上図の青い箱は実際にSDRでサンプルしている領域を、緑の箱は我々がスペクトルを見たい領域を示しています。 LOが95 MHzに設定されているのは、SDRをそのようにチューニングしたからです。 95 MHzは緑の箱の外にあるため、DCスパイクの影響を受けることはありません。

ここで、1つ問題があります。 100 MHz中心で5 MHzの信号だけが欲しい場合でも、周波数シフト、フィルタ処理、そしてダウンサンプリングを自分で行わなければなりません(これらの方法については後ほど学びます)。幸いなことに、このオフチューニング処理はたいていSDRに組み込まれており、SDRが自動的にオフチューニングを行い、目的の中心周波数へと周波数を再シフトしてくれます。この処理をSDR内部で行ってくれることは有益です。なぜなら、USBやEthernet接続でより高いサンプルレートを送る必要がなくなり、最大サンプルレートのボトルネックを回避できるからです。

このDCオフセットに関する節は、本教材が他の教科書と異なる良い例です。一般的なDSPの教科書はサンプリングについては扱っているものの、DCオフセットのような実装上の課題については、しばしば遭遇するにも関わらず多くが触れていません。

SDRを用いたサンプリング¶

サンプリングに関するSDR特有の情報については、以下のいずれかの章をご覧ください。

pluto-chapter の章
usrp-chapter の章

平均電力の計算¶

RF DSPでは、DSPに進む前に信号を検出する時など、信号の電力を計算することがよくあります。平均電力を求めるには、離散的な複素信号、つまりサンプリングされた信号に対して各サンプルの絶対値(大きさ)を取り、それを二乗し、その平均を計算します。

$P = \frac{1}{N} \sum_{n=1}^{N} |x[n]|^2$

ここで、複素数の絶対値とは大きさのことであり、すなわち $\sqrt{I^2+Q^2}$ です。

Pythonでは以下のように平均電力を計算できます。

avg_pwr = np.mean(np.abs(x)**2)

サンプリングされた信号の平均電力を計算するための非常に便利なテクニックがあります。信号が概ねゼロ平均(これはSDRでは通常そうです。後でその理由が説明されます)であれば、信号の分散を取ることで電力を求めることができます。そのような場合、Pythonでは以下で電力を計算できます：

avg_pwr = np.var(x) # (信号は概ねゼロ平均であることを想定)

サンプルの分散が平均電力となる理由はとても簡単です。信号の平均を $\mu$ としたとき、分散は $\frac{1}{N}\sum^N_{n=1} |x[n]-\mu|^2$ です。この式は見覚えがありますよね！もし $\mu$ がゼロであれば、この分散の式は電力の式と等しくなります。また、観測窓(observation window)内のサンプルから平均値を差し引いたうえで分散を取っても構いません。ただし、平均値がゼロでない場合には、分散と電力が一致しない点に注意してください。

パワースペクトル密度の計算¶

前章では、信号をFFTによって周波数領域に変換できることを学びました。そして、その結果はパワースペクトル密度(Power Spectral Density、PSD)と呼ばれます。 PSDは、信号を周波数領域で可視化するための非常に便利なツールであり、多くのDSPアルゴリズムは周波数領域で実行されます。しかし、たくさんのサンプルから実際にPSDを求めてプロットするには、単にFFTを取るだけでは不十分です。 PSDを計算するには、次の6つの処理を行う必要があります。

サンプルに対してFFTを行う。x個のサンプルがあれば、FFTのサイズはxと同じになります。ここでは例として、最初の1024個のサンプルを使って1024サイズのFFTを実行します。出力は1024個の複素浮動小数点数になります。
FFT出力の絶対値を取る。これにより1024個の実数浮動小数点が得られます。
得られた絶対値を二乗して電力を求める。
正規化を行う。すなわち、FFTサイズ( $N$ )とサンプリングレート( $Fs$ )で割る。
$10 \log_{10}()$ を使ってdBに変換する。PSDは常に対数スケールで表示されます。
「0 Hz」が中心に来るようにFFTシフト(前の章で説明)を行い、負の周波数が中心の左側に来るようにする。

以上の6つのステップは、Pythonで以下のように書けます

Fs = 1e6 # サンプリングレートを1 MHzと仮定
# xはIQサンプルの配列とする
N = 1024
x = x[0:N] # 最初の1024サンプルのみFFTの対象とする。下記も参照。
PSD = np.abs(np.fft.fft(x))**2 / (N*Fs)
PSD_log = 10.0*np.log10(PSD)
PSD_shifted = np.fft.fftshift(PSD_log)

周波数領域の章で学んだようにウィンドウ処理を加えても良いです。ウィンドウ処理はFFTをかける直前に行います。

# x = x[0:1024] の行の後に以下を追加
x = x * np.hamming(len(x)) # ハミング窓を適用

このPSDをプロットするには、x軸の値を知る必要があります。前の章で学んだように、信号をサンプリングしたとき、Fsをサンプリングレートとして-Fs/2からFs/2の間のスペクトルだけ「見る」ことができます。周波数分解能はFFTサイズによって決まり、これはデフォルトではFFT処理を行ったサンプル数と同じです。この例では、x軸は -0.5 MHz から 0.5 MHz の間を等間隔に1024分割した点になります。もしSDRを2.4 GHzにチューニングしていた場合、観測窓は2.3995 GHzから2.4005 GHzになります。 Pythonで観測窓をシフトするには次のようにします。

center_freq = 2.4e9 # SDRをチューニングした中心周波数
f = np.arange(Fs/-2.0, Fs/2.0, Fs/N) # # 開始, 終了, ステップ数。0 Hzを中心とする。
f += center_freq # 中心周波数を加算。
plt.plot(f, PSD_shifted)
plt.show()

これで美しきPSDが得られているはずです!

数百万のサンプルに対してPSDを求めたい場合、全100万ポイントに対してFFTをしないでください。永遠に時間がかかりますし、100万個の「周波数ビン(frequency bins)」が出力されるため、どの道プロットにも向きません。代わりに、小さいサイズでPSDを複数回求め、平均を取るかスペクトログラムとして表示するのがおすすめです。あるいは、信号が急激に変化しないことが分かっているなら、数千サンプルだけ使ってPSDを計算するのが適切です。数千のサンプルの時間枠(time-frame)内であれば、信号の特性を見るのに十分なサンプルが得られているでしょう。

以下は、信号(50 Hzの複素指数関数)とノイズを生成してPSDを描画する完全なコード例です。ここでは信号全体にFFTを適用するため、シミュレーションするサンプル数NがそのままFFTサイズになることに注意してください。

import numpy as np
import matplotlib.pyplot as plt

Fs = 300 # サンプルレート
Ts = 1/Fs # サンプル集き
N = 2048 # シミュレーションするサンプル数

t = Ts*np.arange(N)
x = np.exp(1j*2*np.pi*50*t) # 50 Hzの正弦波をシミュレーション

n = (np.random.randn(N) + 1j*np.random.randn(N))/np.sqrt(2) # 単位電力(unity power)の複素ノイズ
noise_power = 2
r = x + n * np.sqrt(noise_power)

PSD = np.abs(np.fft.fft(r))**2 / (N*Fs)
PSD_log = 10.0*np.log10(PSD)
PSD_shifted = np.fft.fftshift(PSD_log)

f = np.arange(Fs/-2.0, Fs/2.0, Fs/N) # 開始, 終了, ステップ数

plt.plot(f, PSD_shifted)
plt.xlabel("Frequency [Hz]")
plt.ylabel("Magnitude [dB]")
plt.grid(True)
plt.show()

出力は以下のようになります。

さらに詳しく知りたい人向けの資料¶

https://web.archive.org/web/20220613052830/http://rfic.eecs.berkeley.edu/~niknejad/ee242/pdf/eecs242_lect3_rxarch.pdf