15. Exemple bout en bout¶
Dans ce chapitre, nous regroupons un grand nombre des concepts que nous avons appris précédemment et nous présentons un exemple complet de réception et de décodage d’un signal numérique réel. Nous allons étudier le système de données radio (RDS pour Radio Data System en anglais), qui est un protocole de communication permettant d’intégrer de petites quantités d’informations dans les émissions de radio FM, comme le nom de la station et de la chanson. Nous devrons démoduler la FM, décaler la fréquence, filtrer, décimer, rééchantillonner, synchroniser, décoder et analyser les octets. Un exemple de fichier IQ est fourni à des fins de test ou si vous n’avez pas de SDR sous la main.
Introduction à la radio FM et au RDS¶
Pour comprendre le RDS, nous devons d’abord examiner les émissions de radio FM et la façon dont leurs signaux sont structurés. Vous connaissez probablement la partie audio des signaux FM, qui sont simplement des signaux audio modulés en fréquence et transmis à des fréquences centrales correspondant au nom de la station, par exemple, “Sud Radio” est centré à exactement 101.8 MHz à Toulouse. En plus de la partie audio, chaque émission FM contient d’autres composants qui sont modulés en fréquence en même temps que l’audio. Au lieu de rechercher la structure du signal sur Google, examinons la densité spectrale de puissance (DSP) d’un exemple de signal FM, après la démodulation FM. Nous ne voyons que la partie positive car la sortie de la démodulation FM est un signal réel, même si l’entrée est complexe (nous verrons bientôt le code pour effectuer cette démodulation).
En regardant le signal dans le domaine de la fréquence, nous remarquons les signaux individuels suivants :
- Un signal de forte puissance entre 0 - 17 kHz
- Un signal sonore à 19 kHz
- Centré à 38 kHz et d’une largeur d’environ 30 kHz, nous voyons un signal symétrique intéressant.
- Signal en forme de double lobe centré à 57 kHz.
- Signal en forme de lobe unique centré à 67 kHz.
C’est essentiellement tout ce que nous sommes en mesure de déterminer en regardant la DSP, et rappelez-vous que c’est après la démodulation FM. La DSP avant la démodulation FM ressemble à ce qui suit, ce qui ne nous dit pas grand-chose.
Ceci étant dit, il est important de comprendre que lorsque vous modulez un signal en FM, une fréquence plus élevée dans le signal de données entraînera une fréquence plus élevée dans le signal FM résultant. Donc, ce signal centré à 67 kHz qui est présent augmente la largeur de bande totale occupée par le signal FM transmis, car la composante de fréquence maximale est maintenant autour de 75 kHz comme le montre le premier PSD ci-dessus. La règle de la largeur de bande de Carson appliquée à la FM nous indique que les stations FM occupent environ 250 kHz du spectre, ce qui explique pourquoi nous échantillonnons généralement à 250 kHz (rappelez-vous que lorsque vous utilisez un échantillonnage en quadrature/IQ, votre largeur de bande reçue est égale à votre taux d’échantillonnage).
En guise d’aparté, certains lecteurs ont peut-être l’habitude d’observer la bande FM à l’aide d’une SDR ou d’un analyseur de spectre et de voir le spectrogramme suivant, et de penser que les signaux en forme de blocs adjacents à certaines des stations FM sont des données RDS.
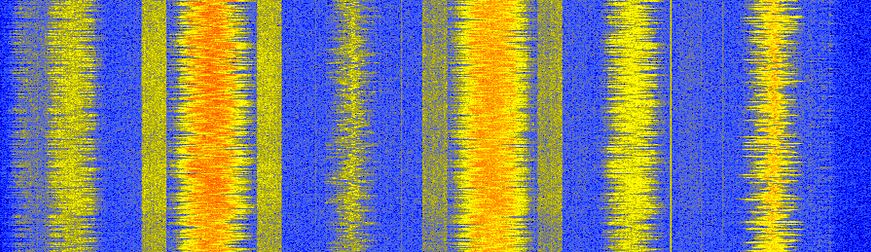
Il s’avère que ces signaux en forme de blocs sont en fait la Radio HD, une version numérique du même signal radio FM (même contenu audio). Cette version numérique permet d’obtenir un signal audio de meilleure qualité au niveau du récepteur car la FM analogique comprendra toujours un certain bruit après démodulation, puisqu’il s’agit d’un schéma analogique, mais le signal numérique peut être démodulé/décodé avec un bruit nul, en supposant qu’il n’y ait aucune erreur de bit.
Revenons aux cinq signaux que nous avons découverts dans notre DSP; le diagramme suivant indique à quoi sert chaque signal.
Je passe en revue chacun de ces signaux sans ordre particulier:
Les signaux audio mono et stéréo transportent simplement le signal audio, dans un schéma où leur addition et leur soustraction vous donnent les canaux gauche et droit.
La tonalité pilote de 19 kHz est utilisée pour démoduler le signal audio stéréo. Si vous doublez la tonalité, elle sert de référence de fréquence et de phase, puisque le signal audio stéréo est centré à 38 kHz. Doubler la tonalité peut être fait en élevant simplement les échantillons au carré, en se rappelant la propriété de Fourier de décalage de fréquence que nous avons apprise dans le chapitre Domaine fréquentiel.
DirectBand était un réseau de diffusion de données sans fil en Amérique du Nord, détenu et exploité par Microsoft, également appelé “MSN Direct” sur les marchés grand public. DirectBand transmettait des informations à des appareils tels que des récepteurs GPS portables, des montres-bracelets et des stations météorologiques domestiques. Il permettait même aux utilisateurs de recevoir des messages courts de Windows Live Messenger. L’une des applications les plus réussies de DirectBand était l’affichage en temps réel de données sur le trafic local sur les récepteurs GPS Garmin, qui étaient utilisés par des millions de personnes avant que les smartphones ne deviennent omniprésents. Le service DirectBand a été fermé en janvier 2012, ce qui soulève la question suivante: pourquoi le voit-on dans nos signaux FM enregistrés après 2012? Ma seule hypothèse est que la plupart des émetteurs FM ont été conçus et construits bien avant 2012, et que même sans “alimentation” DirectBand active, ils transmettent toujours quelque chose, peut-être des symboles de pilotage.
Enfin, nous en arrivons au RDS, qui est l’objet du reste de ce chapitre. Comme nous pouvons le voir dans notre premier PSD, le RDS a une largeur de bande d’environ 4 kHz (avant d’être modulé en FM), et se situe entre le signal audio stéréo et le signal DirectBand. Il s’agit d’un protocole de communication numérique à faible débit de données qui permet aux stations FM d’inclure l’identification de la station, des informations sur le programme, l’heure et d’autres informations diverses à côté du signal audio. La norme RDS est publiée sous le nom de norme IEC 62106 et peut être trouvée ici.
Le signal RDS¶
Dans ce chapitre, nous allons utiliser Python pour recevoir RDS, mais pour mieux comprendre comment le recevoir, nous devons d’abord apprendre comment le signal est formé et transmis.
Côté émission¶
Les informations RDS à transmettre par la station FM (par exemple, le nom de la piste, etc.) sont codées en jeux de 8 octets. Chaque ensemble de 8 octets, qui correspond à 64 bits, est combiné à 40 “bits de contrôle” pour former un seul “groupe”. Ces 104 bits sont transmis ensemble, mais il n’y a pas d’intervalle de temps entre les groupes. Ainsi, du point de vue du récepteur, il reçoit ces bits sans interruption et doit déterminer la limite entre les groupes de 104 bits. Nous verrons plus de détails sur le codage et la structure du message lorsque nous nous plongerons dans la partie réception.
Pour transmettre ces bits sans fil, le RDS utilise la modulation par déplacement de phase (BPSK), qui, comme nous l’avons appris dans le chapitre Modulation numérique, est un schéma de modulation numérique simple utilisé pour associer des 1 et des 0 à la phase d’une porteuse. Comme de nombreux protocoles basés sur la BPSK, le RDS utilise le codage différentiel, ce qui signifie simplement que les 1 et les 0 des données sont codés dans les changements de 1 et de 0, ce qui vous permet de ne plus vous soucier de savoir si vous êtes déphasé de 180 degrés (nous y reviendrons plus tard). Les symboles BPSK sont transmis à 1187,5 symboles par seconde, et comme la BPSK transporte un bit par symbole, cela signifie que le RDS a un débit de données brut d’environ 1,2 kbps (y compris l’overhead). Le RDS ne contient aucun codage de canal (ou correction d’erreur), bien que les paquets de données contiennent un contrôle de redondance cyclique (CRC) pour savoir si une erreur s’est produite. L’utilisateur expérimenté de la BPSK peut se demander pourquoi nous avons vu un signal en forme de double lobe dans la première DSP; la BPSK a généralement un lobe principal. Il s’avère que RDS prend le signal BPSK et le duplique sur la fréquence centrale de 57 kHz, pour plus de robustesse. Lorsque nous nous plongerons dans le code Python utilisé pour recevoir le RDS, l’une de nos étapes consistera à filtrer pour isoler un seul de ces signaux BPSK.
Le signal final “double BPSK” est ensuite décalé en fréquence jusqu’à 57 kHz et ajouté à toutes les autres composantes du signal FM, avant d’être modulé en FM et transmis sur les ondes à la fréquence de la station. Les signaux radio FM sont transmis à une puissance extrêmement élevée par rapport à la plupart des autres communications sans fil, jusqu’à 80 kW! C’est pourquoi de nombreux utilisateurs de la radio logicielle ont un filtre de rejet de la FM (c’est-à-dire un filtre coupe-bande) avec leur antenne, afin que la FM n’ajoute pas d’interférences à ce qu’ils essaient de recevoir.
Il ne s’agissait là que d’un bref aperçu de l’aspect transmission, mais nous entrerons dans les détails lorsque nous aborderons la réception du RDS.
Côté récepteur¶
Afin de démoduler et de décoder le RDS, nous allons effectuer les étapes suivantes, dont beaucoup sont des étapes de transmission en sens inverse (pas besoin de mémoriser cette liste, nous allons parcourir chaque étape individuellement ci-dessous):
- Recevoir un signal radio FM centré sur la fréquence de la station (ou lu dans un enregistrement IQ), généralement à une fréquence d’échantillonnage de 250 kHz
- Démodulez la FM en utilisant ce qu’on appelle la “démodulation en quadrature”.
- Décalage de fréquence de 57 kHz pour que le signal RDS soit centré à 0 Hz.
- Filtre passe-bas, pour filtrer tout ce qui n’est pas RDS.
- Décimation par 10 pour pouvoir travailler à un taux d’échantillonnage plus faible, puisque nous avons de toute façon filtré les hautes fréquences.
- Rééchantillonnage à 19 kHz, ce qui nous donnera un nombre entier d’échantillons par symbole.
- Isolez l’un des deux signaux RDS BPSK avec un filtre passe-bande.
- Synchronisation temporelle au niveau du symbole, en utilisant Mueller et Muller dans cet exemple.
- Synchronisation fine de la fréquence en utilisant une boucle de Costas
- Démodulation du BPSK en 1 et 0.
- Décodage différentiel, pour annuler l’encodage différentiel qui a été appliqué.
- Décodage des 1 et 0 en groupes d’octets.
- Analyse des groupes d’octets dans notre sortie finale.
Bien que cela puisse sembler beaucoup d’étapes, RDS est en fait l’un des protocoles de communication numérique sans fil les plus simples qui soient. Un protocole sans fil moderne comme le WiFi ou la 5G nécessite un manuel entier pour couvrir uniquement les informations de haut niveau de la couche PHY/MAC.
Nous allons maintenant nous plonger dans le code Python utilisé pour recevoir le RDS. Ce code a été testé pour fonctionner en utilisant un enregistrement radio FM que vous pouvez trouver ici, bien que vous devriez être en mesure d’introduire votre propre signal tant qu’il est reçu à un SNR assez élevé, il suffit de régler la fréquence centrale de la station et d’échantillonner à un taux de 250 kHz. Dans cette section, nous présenterons de petites portions du code individuellement, avec une discussion, mais le même code est fourni à la fin de ce chapitre en un grand bloc. Chaque section présentera un bloc de code, puis expliquera ce qu’il fait.
Acquisition d’un signal¶
import numpy as np
from scipy.signal import resample_poly, firwin, bilinear, lfilter
import matplotlib.pyplot as plt
# Lire le signal
x = np.fromfile('/home/marc/Downloads/fm_rds_250k_1Msamples.iq', dtype=np.complex64)
sample_rate = 250e3
center_freq = 99.5e6
Nous avons lu notre enregistrement de test, qui a été échantillonné à 250 kHz et centré sur une station FM reçue à un SNR élevé. Veillez à mettre à jour le chemin du fichier pour refléter votre système et l’endroit où vous avez sauvegardé l’enregistrement. Si vous avez un SDR déjà configuré et fonctionnant depuis Python, n’hésitez pas à recevoir un signal en direct, bien qu’il soit utile d’avoir d’abord testé l’ensemble du code avec un enregistrement de QI connu pour fonctionner. Tout au long de ce code, nous utiliserons x pour stocker le signal à manipuler.
Démodulation FM¶
# Démodulation en quadrature
x = 0.5 * np.angle(x[0:-1] * np.conj(x[1:])) # see https://wiki.gnuradio.org/index.php/Quadrature_Demod
Comme nous l’avons vu au début de ce chapitre, plusieurs signaux individuels sont combinés en fréquence et modulés en FM pour créer ce qui est réellement transmis dans l’air. La première étape consiste donc à annuler cette modulation FM. Une autre façon de voir les choses est que l’information est stockée dans la variation de fréquence du signal que nous recevons, et nous voulons le démoduler pour que l’information soit maintenant dans l’amplitude et non dans la fréquence. Notez que la sortie de cette démodulation est un signal réel, même si nous avons introduit un signal complexe.
Ce que fait cette simple ligne de Python, c’est d’abord calculer le produit de notre signal avec une version retardée et conjuguée de notre signal. Ensuite, elle trouve la phase de chaque échantillon dans ce résultat, qui est le moment où il passe de complexe à réel. Pour nous prouver que cela nous donne l’information contenue dans les variations de fréquence, considérons un son à la fréquence \(f\) avec une phase arbitraire \(\phi\), que nous pouvons représenter comme \(e^{j2 \pi (f t + \phi)}\). En temps discret, on utilise un entier \(n\) au lieu de \(t\), cela devient \(e^{j2 \pi (f n + \phi)}\). La version conjuguée et retardée est \(e^{-j2 \pi (f (n-1) + \phi)}\). En multipliant les deux, on obtient \(e^{j2 \pi f}\), ce qui est génial car \(\phi\) a disparu, et quand on calcule la phase de cette expression, il ne reste que \(f\).
Un effet secondaire pratique de la modulation FM est que les variations d’amplitude du signal reçu ne modifient pas réellement le volume de l’audio, contrairement à la radio AM.
Déplacement de fréquence¶
# décalage de freq
N = len(x)
f_o = -57e3 # valeur du décalage
t = np.arange(N)/sample_rate # vecteur de temps
x = x * np.exp(2j*np.pi*f_o*t) # décalage de freq
Ensuite, nous décalons la fréquence de 57 kHz vers le bas, en utilisant l’astuce \(e^{j2 \pi f_ot}\) que nous avons apprise dans le chapitre Synchronisation où f_o est le décalage de fréquence en Hz et t est juste un vecteur temps, le fait qu’il commence à 0 n’est pas important, ce qui compte c’est qu’il utilise la bonne période d’échantillonnage (qui est l’inverse du taux d’échantillonnage). Par ailleurs, comme il s’agit d’un signal réel, il n’est pas important d’utiliser une fréquence de -57 ou +57 kHz car les fréquences négatives correspondent aux positives, donc dans tous les cas, notre RDS sera décalé à 0 Hz.
Filtrer pour isoler le RDS¶
# filtre passe bas
taps = firwin(numtaps=101, cutoff=7.5e3, fs=sample_rate)
x = np.convolve(x, taps, 'valid')
Maintenant, nous devons filtrer tout ce qui n’est pas RDS. Puisque nous avons un RDS centré à 0 Hz, cela signifie qu’un filtre passe-bas est celui que nous voulons. Nous utilisons firwin() pour concevoir un filtre FIR (c’est-à-dire, trouver les taps), qui a juste besoin de savoir combien de taps nous voulons pour le filtre, et la fréquence de coupure. La fréquence d’échantillonnage doit également être fournie, sinon la fréquence de coupure n’a pas de sens pour firwin. Le résultat est un filtre passe-bas symétrique, donc nous savons que les taps seront des nombres réels, et nous pouvons appliquer le filtre à notre signal en utilisant une convolution. Nous choisissons 'valid' pour nous débarrasser des effets de bord de la convolution, bien que dans ce cas, cela n’ait pas vraiment d’importance parce que nous introduisons un signal si long que quelques échantillons bizarres sur l’un ou l’autre des bords ne vont rien gâcher.
Decimer par 10¶
# Décimer par 10, maintenant que nous avons filtré et qu'il n'y aura pas de repliement.
x = x[::10]
sample_rate = 25e3
Chaque fois que vous filtrez jusqu’à une petite fraction de votre bande passante (par exemple, nous avons commencé avec 125 kHz de bande passante réelle et n’avons sauvegardé que 7.5 kHz de celle-ci), il est logique de décimer. Rappelez-vous le début du chapitre échantillonnage IQ où nous avons appris le taux de Nyquist et la possibilité de stocker entièrement des informations à bande limitée tant que nous échantillonnions à deux fois la fréquence la plus élevée. Maintenant que nous avons utilisé notre filtre passe-bas, notre fréquence la plus élevée est d’environ 7.5 kHz, donc nous n’avons besoin que d’une fréquence d’échantillonnage de 15 kHz. Par sécurité, nous allons ajouter un peu de marge et utiliser une nouvelle fréquence d’échantillonnage de 25 kHz (ce qui s’avère être une bonne solution mathématique par la suite).
Nous effectuons la décimation en éliminant simplement 9 échantillons sur 10, puisque nous étions précédemment à un taux d’échantillonnage de 250 kHz et que nous voulons qu’il soit maintenant à 25 kHz. Cela peut sembler déroutant au premier abord, car en éliminant 90% des échantillons, on a l’impression de perdre de l’information, mais si vous relisez le chapitre échantillonnage IQ, vous verrez pourquoi nous ne perdons rien en fait, car nous avons filtré correctement (ce qui a agi comme notre filtre anti-repliement) et réduit notre fréquence maximale et donc la largeur de bande du signal.
Du point de vue du code, c’est probablement l’étape la plus simple de toutes, mais assurez-vous de mettre à jour votre variable sample_rate pour refléter le nouveau taux d’échantillonnage.
Rééchantillonnage à 19 kHz¶
# Rééchantillonnage à 19 kHz
x = resample_poly(x, 19, 25) # up, down
sample_rate = 19e3
Dans le chapitre Mise en Forme nous avons solidifié le concept “d’échantillons par symbole”, et appris la commodité d’avoir un nombre entier d’échantillons par symbole (une valeur fractionnaire est valide, mais pas pratique). Comme nous l’avons mentionné précédemment, le RDS utilise une BPSK transmettant 1187.5 symboles par seconde. Si nous continuons à utiliser notre signal tel quel, échantillonné à 25 kHz, nous aurons 21.052631579 échantillons par symbole (faites une pause et réfléchissez au calcul si cela n’a pas de sens). Ce que nous voulons vraiment, c’est une fréquence d’échantillonnage qui soit un multiple entier de 1187.5 Hz, mais nous ne pouvons pas aller trop bas ou nous ne serons pas en mesure de “stocker” toute la largeur de bande de notre signal. Dans la sous-section précédente, nous avons expliqué que nous avions besoin d’une fréquence d’échantillonnage de 15 kHz ou plus, et nous avons choisi 25 kHz juste pour nous donner une certaine marge.
Trouver la meilleure fréquence d’échantillonnage pour rééchantillonner se résume à savoir combien d’échantillons par symbole nous voulons. Hypothétiquement, envisageons de viser 10 échantillons par symbole. Le taux de symbole RDS de 1187.5 multiplié par 10 nous donnerait un taux d’échantillonnage de 11.875 kHz, ce qui n’est malheureusement pas assez élevé pour Nyquist. Que diriez-vous de 13 échantillons par symbole? 1187.5 multiplié par 13 nous donne 15437.5 Hz, ce qui est supérieur à 15 kHz, mais un nombre assez inégal. Que diriez-vous de la puissance de 2 suivante, soit 16 échantillons par symbole? 1187.5 multiplié par 16 est exactement 19 kHz! Le nombre pair est moins une coïncidence qu’un choix de conception du protocole.
Pour rééchantillonner de 25 kHz à 19 kHz, nous utilisons resample_poly() qui suréchantillonne par une valeur entière, filtre, puis sous-échantillonne par une valeur entière. C’est pratique car au lieu d’entrer 25000 et 19000, nous pouvons utiliser 25 et 19. Si nous avions utilisé 13 échantillons par symbole en utilisant une fréquence d’échantillonnage de 15437.5 Hz, nous ne pourrions pas utiliser resample_poly() et le processus de rééchantillonnage serait beaucoup plus compliqué.
Encore une fois, n’oubliez jamais de mettre à jour votre variable sample_rate lorsque vous effectuez une opération qui la modifie.
Filtre passe-bande¶
# Filtre passe-bande pour isoler un signal RDS BPSK
taps = firwin(numtaps=501, cutoff=[0.05e3, 2e3], fs=sample_rate, pass_zero=False)
x = np.convolve(x, taps, 'valid')
Rappelons que le RDS contient deux signaux BPSK identiques, d’où la forme que nous avons vue dans la PSD au début. Nous devons en choisir un, donc nous allons arbitrairement décider de garder le positif avec un filtre passe-bande. Nous utilisons firwin() à nouveau, mais notez le pass_zero=False qui indique que vous voulez un filtre passe-bande plutôt qu’un filtre passe-bas, et il y a deux fréquences de coupure pour définir la bande. Le signal s’étend approximativement de 0 Hz à 2 kHz mais vous ne pouvez pas spécifier une fréquence de départ de 0 Hz donc nous utilisons 0.05 kHz. Enfin, nous devons augmenter le nombre de taps, pour obtenir une réponse en fréquence plus abrupte. Nous pouvons vérifier que ces chiffres ont fonctionné en examinant notre filtre dans le domaine temporel (en traçant les taps) et dans le domaine fréquentiel (en prenant la FFT des taps). Notez comment dans le domaine fréquentiel, nous atteignons une réponse proche de zéro à environ 0 Hz.
Remarque: à un moment ou à un autre, je mettrai à jour le filtre ci-dessus pour utiliser un filtre adapté (le root-raised cosine, je crois que c’est ce que RDS utilise), pour des raisons conceptuelles, mais j’ai obtenu les mêmes taux d’erreur en utilisant l’approche firwin() que le filtre adapté de GNU Radio, donc ce n’est clairement pas une exigence stricte.
Synchronisation en temps (niveau symbole)¶
# Synchronisation des symboles, en utilisant ce que nous avons fait dans le chapitre sur la synchronisation.
samples = x # comme dans le chapitre de la synchronisation
samples_interpolated = resample_poly(samples, 32, 1) # Nous utiliserons 32 comme facteur d'interpolation, choisi arbitrairement.
sps = 16
mu = 0.01 # estimation initiale de la phase de l'échantillon
out = np.zeros(len(samples) + 10, dtype=np.complex64)
out_rail = np.zeros(len(samples) + 10, dtype=np.complex64) # stocke les valeurs, à chaque itération nous avons besoin des 2 valeurs précédentes plus la valeur actuelle.
i_in = 0 # index des échantillons d'entrée
i_out = 2 # indice de sortie (les deux premières sorties sont 0)
while i_out < len(samples) and i_in+32 < len(samples):
out[i_out] = samples_interpolated[i_in*32 + int(mu*32)] # prendre ce que nous pensons être le "meilleur" échantillon
out_rail[i_out] = int(np.real(out[i_out]) > 0) + 1j*int(np.imag(out[i_out]) > 0)
x = (out_rail[i_out] - out_rail[i_out-2]) * np.conj(out[i_out-1])
y = (out[i_out] - out[i_out-2]) * np.conj(out_rail[i_out-1])
mm_val = np.real(y - x)
mu += sps + 0.01*mm_val
i_in += int(np.floor(mu)) # arrondir à l'entier le plus proche puisque nous l'utilisons comme un index
mu = mu - np.floor(mu) # supprimer la partie entière de mu
i_out += 1 # incrémenter l'indice de sortie
x = out[2:i_out] # supprimer les deux premiers, et tout ce qui suit i_out (qui n'a jamais été rempli)
Nous sommes enfin prêts pour notre synchronisation temps symbole, ici nous utiliserons exactement le même code de synchronisation de Mueller et Muller du chapitre Synchronisation, rendez-vous y si vous voulez en savoir plus sur son fonctionnement. Nous avons fixé l’échantillon par symbole (sps) à 16 comme discuté précédemment. Une valeur de gain de 0.01 a été trouvée par expérimentation pour fonctionner correctement. La sortie devrait maintenant être un échantillon par symbole, c’est-à-dire que notre sortie est nos “symboles souples”, avec un éventuel décalage de fréquence inclus. L’animation suivante de la constellation est utilisée pour vérifier que nous obtenons des symboles BPSK (avec un décalage de fréquence provoquant une rotation) :
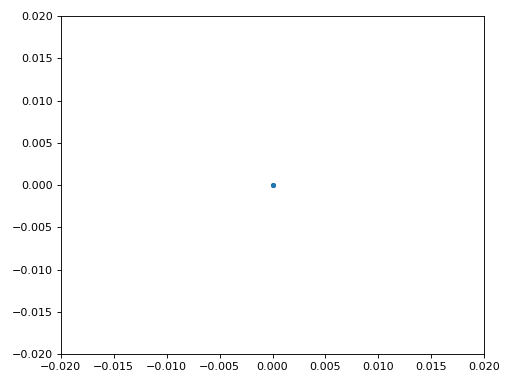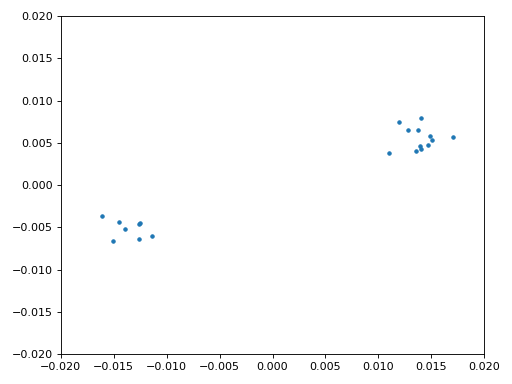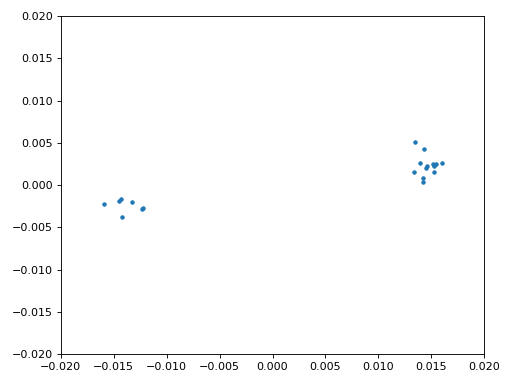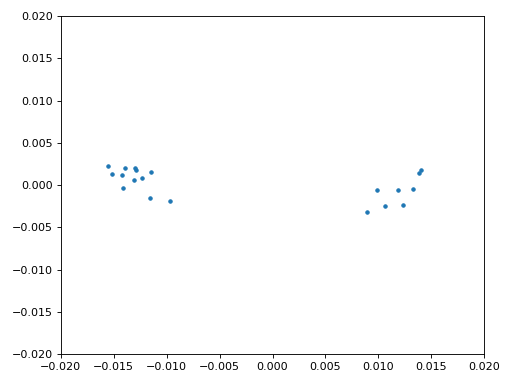
Si vous utilisez votre propre signal FM et que vous n’obtenez pas deux groupes distincts d’échantillons complexes à ce stade, cela signifie que la synchronisation du symbole ci-dessus n’a pas réussi à atteindre la synchronisation, ou qu’il y a un problème avec l’une des étapes précédentes. Vous n’avez pas besoin d’animer la constellation, mais si vous la tracez, veillez à ne pas tracer tous les échantillons, car cela ressemblera à un cercle. Si vous ne tracez que 100 ou 200 échantillons à la fois, vous aurez une meilleure idée de la présence ou non de deux groupes de points, même si elles tournent.
Synchronisation fine de la fréquence¶
# Synchronisation fine de la fréquence
samples = x # comme dans le chapitre de la synchro
N = len(samples)
phase = 0
freq = 0
# Ces deux paramètres suivants sont ce qu'il faut ajuster, pour rendre la boucle de rétroaction plus rapide ou plus lente (ce qui a un impact sur la stabilité).
alpha = 8.0
beta = 0.002
out = np.zeros(N, dtype=np.complex64)
freq_log = []
for i in range(N):
out[i] = samples[i] * np.exp(-1j*phase) # ajuster l'échantillon d'entrée par l'inverse du décalage de phase estimé
error = np.real(out[i]) * np.imag(out[i]) # Voici la formule d'erreur pour une boucle de Costas de 2ème ordre (par exemple pour BPSK)
# Avancer la boucle (recalculer la phase et le décalage de fréquence)
freq += (beta * error)
freq_log.append(freq * sample_rate / (2*np.pi)) # convertir de la vitesse angulaire en Hz pour les logs
phase += freq + (alpha * error)
# Facultatif : Ajustez la phase pour qu'elle soit toujours comprise entre 0 et 2pi, rappelez-vous que la phase tourne autour 2pi
while phase >= 2*np.pi:
phase -= 2*np.pi
while phase < 0:
phase += 2*np.pi
x = out
Nous allons également copier le code Python de synchronisation fine de fréquence du chapitre Synchronisation, qui utilise une boucle de Costas pour supprimer tout décalage de fréquence résiduel, ainsi que pour aligner notre BPSK sur l’axe réel (I), en forçant Q à être aussi proche de zéro que possible. Tout ce qui reste dans Q est probablement dû au bruit du signal, en supposant que la boucle de Costas a été réglée correctement. Juste pour le plaisir, regardons la même animation que ci-dessus, mais après que la synchronisation de fréquence ait été effectuée (plus de rotation !) :
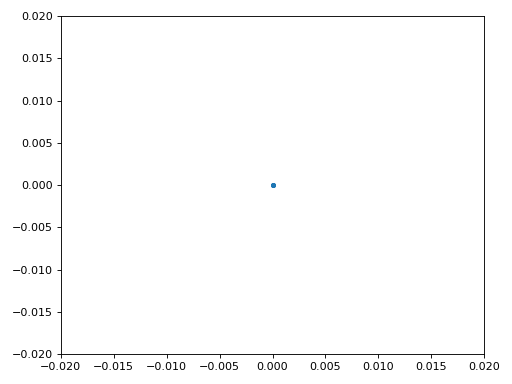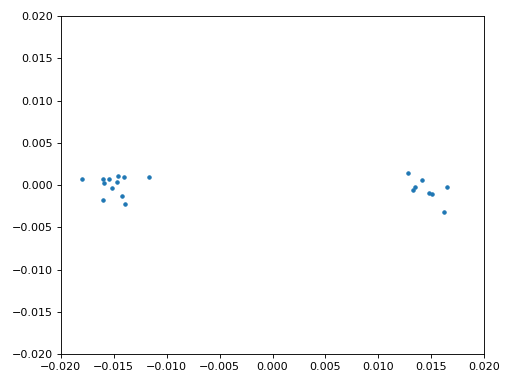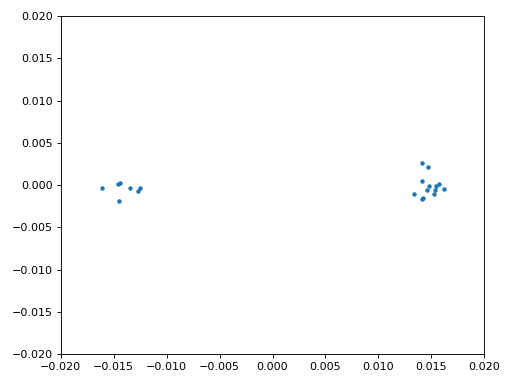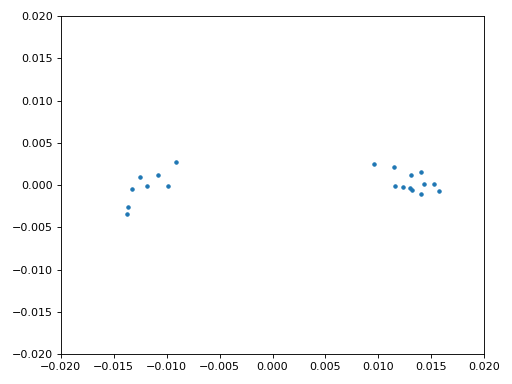
De plus, nous pouvons regarder l’erreur de fréquence estimée dans le temps pour voir le fonctionnement de la boucle de Costas, notez comment nous l’avons enregistrée dans le code ci-dessus. Il semble qu’il y avait environ 13 Hz de décalage de fréquence, soit à cause de l’oscillateur local (LO) de l’émetteur qui était éteint, soit à cause de l’OL du récepteur (plus probablement le récepteur). Si vous utilisez votre propre signal FM, vous devrez peut-être modifier alpha et beta jusqu’à ce que la courbe soit similaire, elle devrait atteindre la synchronisation assez rapidement (par exemple, quelques centaines de symboles) et la maintenir avec un minimum d’oscillations. Le modèle que vous voyez ci-dessous après qu’il ait trouvé son état stable est une gigue de fréquence, pas une oscillation.
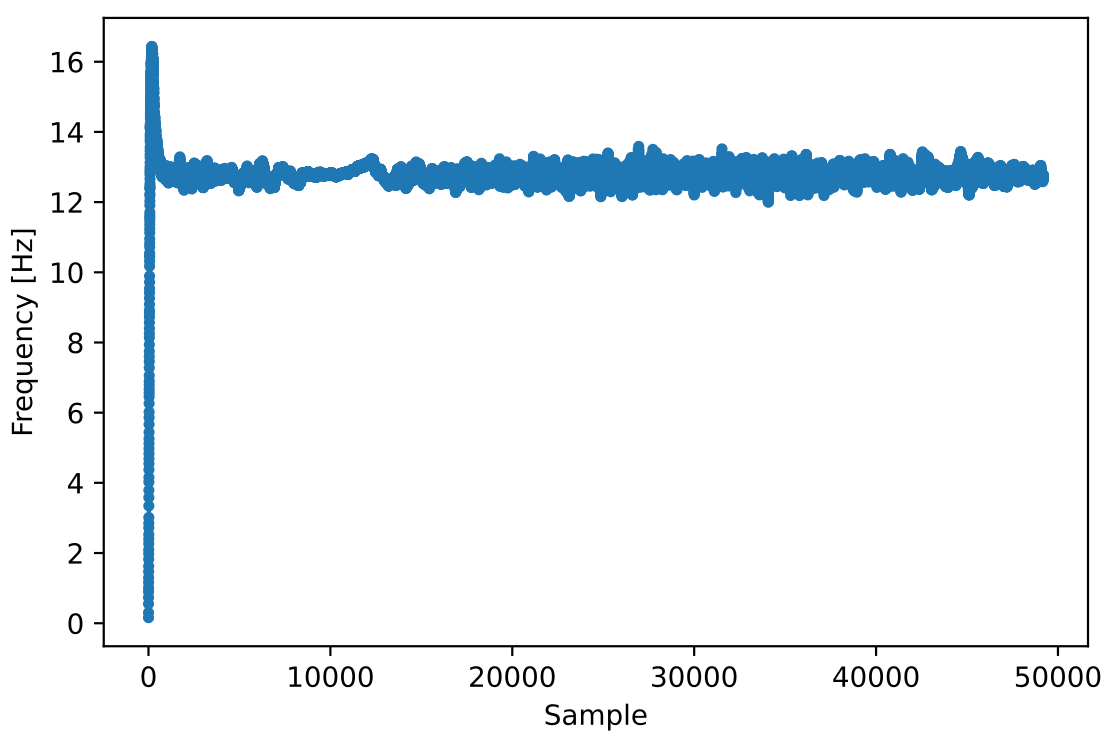
Démoduler le BPSK¶
# Demodulation BPSK
bits = (np.real(x) > 0).astype(int) # 1s et 0s
La démodulation du BPSK à ce stade est très facile, rappelez-vous que chaque échantillon représente un symbole souple, donc tout ce que nous avons à faire est de vérifier si chaque échantillon est au-dessus ou au-dessous de 0. Le .astype(int) est juste pour que nous puissions travailler avec un tableau d’entiers au lieu d’un tableau de booléens. Vous pouvez vous demander si au-dessus ou au-dessous de zéro représente un 1 ou un 0. Comme vous le verrez à l’étape suivante, cela n’a pas d’importance!
Décodage différentiel¶
# Décodage différentiel, de sorte qu'il importe peu que notre BPSK ait subi une rotation de 180 degrés sans que nous nous en rendions compte.
bits = (bits[1:] - bits[0:-1]) % 2
bits = bits.astype(np.uint8) # decodage
Le signal BPSK a utilisé un codage différentiel lors de sa création, ce qui signifie que chaque 1 et 0 des données d’origine a été transformé de telle sorte qu’un changement de 1 à 0 ou de 0 à 1 a été mis en correspondance avec un 1, et aucun changement n’a été mis en correspondance avec un 0. L’avantage de l’utilisation du codage différentiel est que vous n’avez pas à vous soucier des rotations de 180 degrés lors de la réception de la BPSK, car le fait que nous considérions qu’un 1 est supérieur ou inférieur à zéro n’a plus d’impact, ce qui compte c’est le changement entre 1 et 0. Ce concept peut être plus facile à comprendre en regardant un exemple de données, ci-dessous les 10 premiers symboles avant et après le décodage différentiel :
[1 1 1 1 0 1 0 0 1 1] # avant le décodage différentiel
[- 0 0 0 1 1 1 0 1 0] # après le décodage différentiel
Décodage RDS¶
Nous avons enfin nos bits d’information, et nous sommes prêts à décoder leur signification! L’énorme bloc de code fourni ci-dessous est ce que nous allons utiliser pour décoder les 1 et les 0 en groupes d’octets. Cette partie aurait beaucoup plus de sens si nous avions d’abord créé la partie émetteur du RDS, mais pour l’instant, sachez simplement qu’en RDS, les octets sont regroupés en groupes de 12 octets, où les 8 premiers représentent les données et les 4 derniers servent de mot de synchronisation (appelés “mots de décalage”). Les 4 derniers octets ne sont pas nécessaires à l’étape suivante (l’analyseur syntaxique), nous ne les incluons donc pas dans la sortie. Ce bloc de code prend les 1 et 0 créés ci-dessus (sous la forme d’un tableau 1D d’uint8) et produit une liste de listes d’octets (une liste de 8 octets où ces 8 octets sont dans une liste). Ceci est pratique pour l’étape suivante, qui va itérer à travers la liste de 8 octets, un groupe de 8 à la fois.
La plupart du code de décodage ci-dessous tourne autour de la synchronisation (au niveau de l’octet, pas du symbole) et de la vérification des erreurs. Il fonctionne par blocs de 104 bits, chaque bloc est soit reçu correctement soit en erreur (en utilisant le CRC pour vérifier), et tous les 50 blocs il vérifie si plus de 35 d’entre eux ont été reçus avec une erreur, auquel cas il réinitialise tout et tente de se synchroniser à nouveau. Le CRC est effectué en utilisant une vérification sur 10 bits, avec le polynôme \(x^{10}+x^8+x^7+x^5+x^4+x^3+1\); cela se produit lorsque reg est xor avec 0x5B9 qui est l’équivalent binaire de ce polynôme. En Python, les opérateurs binaires pour [and, or, not, xor] sont & | ~ ^ respectivement, exactement comme en C++. Un décalage de bit gauche est x << y (comme la multiplication de x par 2**y), et un décalage de bit droit est x >> y (comme la division de x par 2**y), également comme en C++.
Notez que vous n’avez pas besoin de parcourir tout ce code, ou une partie de celui-ci, surtout si vous vous concentrez sur l’apprentissage de la couche physique (PHY) du DSP et de la SDR, car cela ne représente pas le traitement du signal. Ce code est simplement une implémentation d’un décodeur RDS, et essentiellement rien de ce code ne peut être réutilisé pour d’autres protocoles, car il est tellement spécifique à la façon dont le RDS fonctionne. Si vous êtes déjà un peu épuisé par ce chapitre, sentez-vous libre de sauter cet énorme bloc de code qui a un travail assez simple mais qui le fait d’une manière complexe.
# Constantes
syndrome = [383, 14, 303, 663, 748]
offset_pos = [0, 1, 2, 3, 2]
offset_word = [252, 408, 360, 436, 848]
# regardez Annex B, page 64 du standard
def calc_syndrome(x, mlen):
reg = 0
plen = 10
for ii in range(mlen, 0, -1):
reg = (reg << 1) | ((x >> (ii-1)) & 0x01)
if (reg & (1 << plen)):
reg = reg ^ 0x5B9
for ii in range(plen, 0, -1):
reg = reg << 1
if (reg & (1 << plen)):
reg = reg ^ 0x5B9
return reg & ((1 << plen) - 1) # sélectionner les plen bits de reg les plus bas
# Initialiser toutes les variables de travail dont nous aurons besoin pendant la boucle.
synced = False
presync = False
wrong_blocks_counter = 0
blocks_counter = 0
group_good_blocks_counter = 0
reg = np.uint32(0) # était unsigned long en C++ (64 bits) mais numpy ne supporte pas les opérations bit à bit de uint64, je ne pense pas qu'il atteigne cette valeur de toute façon.
lastseen_offset_counter = 0
lastseen_offset = 0
# le processus de synchronisation est décrit dans l'annexe C, page 66 de la norme */
bytes_out = []
for i in range(len(bits)):
# en C++, reg n'est pas initié, il sera donc aléatoire au début, pour le nôtre, il s'agit de 0.
# C'était aussi un unsigned long mais il ne semblait pas s'approcher de la valeur maximale.
# les bits sont soit 0 soit 1
reg = np.bitwise_or(np.left_shift(reg, 1), bits[i]) # reg contient les 26 derniers bits de RDS. Ce sont tous deux des opérations par bit.
if not synced:
reg_syndrome = calc_syndrome(reg, 26)
for j in range(5):
if reg_syndrome == syndrome[j]:
if not presync:
lastseen_offset = j
lastseen_offset_counter = i
presync = True
else:
if offset_pos[lastseen_offset] >= offset_pos[j]:
block_distance = offset_pos[j] + 4 - offset_pos[lastseen_offset]
else:
block_distance = offset_pos[j] - offset_pos[lastseen_offset]
if (block_distance*26) != (i - lastseen_offset_counter):
presync = False
else:
print('Etat de la synchronisation détecté')
wrong_blocks_counter = 0
blocks_counter = 0
block_bit_counter = 0
block_number = (j + 1) % 4
group_assembly_started = False
synced = True
break # syndrome trouvé, plus de cycles
else: # SYNCHRONISÉ
# attendre que 26 bits entrent dans le tampon */
if block_bit_counter < 25:
block_bit_counter += 1
else:
good_block = False
dataword = (reg >> 10) & 0xffff
block_calculated_crc = calc_syndrome(dataword, 16)
checkword = reg & 0x3ff
if block_number == 2: # gérer le cas particulier du mot de décalage C ou C'.
block_received_crc = checkword ^ offset_word[block_number]
if (block_received_crc == block_calculated_crc):
good_block = True
else:
block_received_crc = checkword ^ offset_word[4]
if (block_received_crc == block_calculated_crc):
good_block = True
else:
wrong_blocks_counter += 1
good_block = False
else:
block_received_crc = checkword ^ offset_word[block_number] # xor binaire
if block_received_crc == block_calculated_crc:
good_block = True
else:
wrong_blocks_counter += 1
good_block = False
# Vérification du CRC terminée
if block_number == 0 and good_block:
group_assembly_started = True
group_good_blocks_counter = 1
group = bytearray(8) # 8 octets remplis de 0
if group_assembly_started:
if not good_block:
group_assembly_started = False
else:
# octets de données brutes, tels que reçus du RDS. 8 octets d'information, suivis de 4 caractères de décalage RDS : ABCD/ABcD/EEEE (aux Etats-Unis) que nous laissons de côté ici.
# Mots d'information RDS
# le numéro de bloc est soit 0,1,2,3 donc c'est comme ça qu'on remplit les 8 octets
group[block_number*2] = (dataword >> 8) & 255
group[block_number*2+1] = dataword & 255
group_good_blocks_counter += 1
#print('group_good_blocks_counter:', group_good_blocks_counter)
if group_good_blocks_counter == 5:
#print(group)
bytes_out.append(group) # liste de listes d'octets de longueur 8
block_bit_counter = 0
block_number = (block_number + 1) % 4
blocks_counter += 1
if blocks_counter == 50:
if wrong_blocks_counter > 35: # Autant de blocs erronés doivent signifier que nous avons perdu la synchronisation.
print("Perte de synchronisation (obtient ", wrong_blocks_counter, " mauvais blocs sur ", blocks_counter, " en total)")
synced = False
presync = False
else:
print("Toujours synchronisé (obtient ", wrong_blocks_counter, " mauvais blocs sur ", blocks_counter, " en total)")
blocks_counter = 0
wrong_blocks_counter = 0
Vous trouverez ci-dessous un exemple de sortie de cette étape de décodage. Notez que dans cet exemple, la synchronisation est assez rapide, mais qu’elle est perdue plusieurs fois pour une raison quelconque, bien qu’elle soit toujours capable d’analyser toutes les données comme nous le verrons. Si vous utilisez le fichier d’échantillons téléchargeable de 1M échantillons, vous ne verrez que les premières lignes ci-dessous. Le contenu réel de ces octets ressemble à des nombres/caractères aléatoires selon la façon dont vous les affichez, mais dans l’étape suivante, nous allons les analyser en informations lisibles par l’homme!
Etat de la synchronisation détecté
Toujours synchronisé (obtient 0 mauvais blocs sur 50 en total)
Toujours synchronisé (obtient 0 mauvais blocs sur 50 en total)
Toujours synchronisé (obtient 0 mauvais blocs sur 50 en total)
Toujours synchronisé (obtient 0 mauvais blocs sur 50 en total)
Toujours synchronisé (obtient 1 mauvais blocs sur 50 en total)
Toujours synchronisé (obtient 5 mauvais blocs sur 50 en total)
Toujours synchronisé (obtient 26 mauvais blocs sur 50 en total)
Perte de synchronisation (obtient 50 mauvais blocs sur 50 en total)
Etat de la synchronisation détecté
Toujours synchronisé (obtient 3 mauvais blocs sur 50 en total)
Toujours synchronisé (obtient 0 mauvais blocs sur 50 en total)
Toujours synchronisé (obtient 0 mauvais blocs sur 50 en total)
Toujours synchronisé (obtient 0 mauvais blocs sur 50 en total)
Toujours synchronisé (obtient 0 mauvais blocs sur 50 en total)
Toujours synchronisé (obtient 0 mauvais blocs sur 50 en total)
Toujours synchronisé (obtient 0 mauvais blocs sur 50 en total)
Toujours synchronisé (obtient 0 mauvais blocs sur 50 en total)
Toujours synchronisé (obtient 0 mauvais blocs sur 50 en total)
Toujours synchronisé (obtient 0 mauvais blocs sur 50 en total)
Toujours synchronisé (obtient 0 mauvais blocs sur 50 en total)
Toujours synchronisé (obtient 0 mauvais blocs sur 50 en total)
Toujours synchronisé (obtient 0 mauvais blocs sur 50 en total)
Toujours synchronisé (obtient 0 mauvais blocs sur 50 en total)
Toujours synchronisé (obtient 0 mauvais blocs sur 50 en total)
Toujours synchronisé (obtient 0 mauvais blocs sur 50 en total)
Toujours synchronisé (obtient 0 mauvais blocs sur 50 en total)
Toujours synchronisé (obtient 0 mauvais blocs sur 50 en total)
Toujours synchronisé (obtient 0 mauvais blocs sur 50 en total)
Toujours synchronisé (obtient 0 mauvais blocs sur 50 en total)
Toujours synchronisé (obtient 0 mauvais blocs sur 50 en total)
Toujours synchronisé (obtient 0 mauvais blocs sur 50 en total)
Toujours synchronisé (obtient 2 mauvais blocs sur 50 en total)
Toujours synchronisé (obtient 1 mauvais blocs sur 50 en total)
Toujours synchronisé (obtient 20 mauvais blocs sur 50 en total)
Perte de synchronisation (obtient 47 mauvais blocs sur 50 en total)
Etat de la synchronisation détecté
Toujours synchronisé (obtient 32 mauvais blocs sur 50 en total)
Analyse du RDS¶
Maintenant que nous avons des octets, par groupes de 8, nous pouvons extraire les données finales, c’est-à-dire la sortie finale qui est compréhensible par l’homme. C’est ce qu’on appelle l’analyse des octets, et tout comme le décodeur de la section précédente, il s’agit simplement d’une mise en œuvre du protocole RDS, et il n’est pas vraiment important de le comprendre. Heureusement, ce n’est pas une tonne de code, si vous n’incluez pas les deux tables définies au début, qui sont simplement les tables de recherche pour le type de canal FM et la zone de couverture.
Pour ceux qui veulent apprendre comment ce code fonctionne, je vais fournir quelques informations supplémentaires. Le protocole utilise le concept de drapeau A/B, ce qui signifie que certains messages sont marqués A et d’autres B, et que l’analyse syntaxique change en fonction de ces derniers (le fait qu’il s’agisse de A ou de B est stocké dans le troisième bit du deuxième octet). Il utilise également différents types de “groupes” qui sont analogues au type de message, et dans ce code, nous n’analysons que le type de message 2, qui est le type de message contenant le texte de la radio, qui est la partie intéressante, c’est le texte qui défile sur l’écran de votre voiture. Nous serons toujours en mesure d’analyser le type de chaîne et la région, car ils sont stockés dans chaque message. Enfin, notez que radiotext est une chaîne qui est initialisée à tous les espaces, se remplit lentement au fur et à mesure que les octets sont analysés, puis se réinitialise à tous les espaces si un ensemble spécifique d’octets est reçu. Si vous êtes curieux de savoir quels autres types de messages existent, la liste est la suivante : [“BASIC”, “PIN/SL”, “RT”, “AID”, “CT”, “TDC”, “IH”, “RP”, “TMC”, “EWS”, “EON”]. Le message “RT” est un radiotexte qui est le seul que nous décodons. Le bloc RDS GNU Radio décode aussi “BASIC”, mais pour les stations que j’ai utilisées pour les tests, il ne contenait pas beaucoup d’informations intéressantes, et aurait ajouté beaucoup de lignes au code ci-dessous.
# Annexe F de la norme RBDS Tableau F.1 (Amérique du Nord) et Tableau F.2 (Europe)
# Europe Amérique du Nord
pty_table = [["Undefined", "Undefined"],
["News", "News"],
["Current Affairs", "Information"],
["Information", "Sports"],
["Sport", "Talk"],
["Education", "Rock"],
["Drama", "Classic Rock"],
["Culture", "Adult Hits"],
["Science", "Soft Rock"],
["Varied", "Top 40"],
["Pop Music", "Country"],
["Rock Music", "Oldies"],
["Easy Listening", "Soft"],
["Light Classical", "Nostalgia"],
["Serious Classical", "Jazz"],
["Other Music", "Classical"],
["Weather", "Rhythm & Blues"],
["Finance", "Soft Rhythm & Blues"],
["Children’s Programmes", "Language"],
["Social Affairs", "Religious Music"],
["Religion", "Religious Talk"],
["Phone-In", "Personality"],
["Travel", "Public"],
["Leisure", "College"],
["Jazz Music", "Spanish Talk"],
["Country Music", "Spanish Music"],
["National Music", "Hip Hop"],
["Oldies Music", "Unassigned"],
["Folk Music", "Unassigned"],
["Documentary", "Weather"],
["Alarm Test", "Emergency Test"],
["Alarm", "Emergency"]]
pty_locale = 1 # mis à 0 pour l'Europe qui utilisera la première colonne à la place.
# page 72, Annex D, table D.2 in the standard
coverage_area_codes = ["Local",
"International",
"National",
"Supra-regional",
"Regional 1",
"Regional 2",
"Regional 3",
"Regional 4",
"Regional 5",
"Regional 6",
"Regional 7",
"Regional 8",
"Regional 9",
"Regional 10",
"Regional 11",
"Regional 12"]
radiotext_AB_flag = 0
radiotext = [' ']*65
first_time = True
for group in bytes_out:
group_0 = group[1] | (group[0] << 8)
group_1 = group[3] | (group[2] << 8)
group_2 = group[5] | (group[4] << 8)
group_3 = group[7] | (group[6] << 8)
group_type = (group_1 >> 12) & 0xf # voici ce que chacun signifie, par exemple RT est radiotexte qui est le seul que nous décodons ici : ["BASIC", "PIN/SL", "RT", "AID", "CT", "TDC", "IH", "RP", "TMC", "EWS", "___", "___", "___", "___", "EON", "___"]
AB = (group_1 >> 11 ) & 0x1 # b si 1, a si 0
#print("group_type:", group_type) # il s'agit essentiellement du type de message, je ne vois que les types 0 et 2 dans mon enregistrement.
#print("AB:", AB)
program_identification = group_0 # "PI"
program_type = (group_1 >> 5) & 0x1f # "PTY"
pty = pty_table[program_type][pty_locale]
pi_area_coverage = (program_identification >> 8) & 0xf
coverage_area = coverage_area_codes[pi_area_coverage]
pi_program_reference_number = program_identification & 0xff # juste un entier
if first_time:
print("PTY:", pty)
print("program:", pi_program_reference_number)
print("coverage_area:", coverage_area)
first_time = False
if group_type == 2:
# lorsque le flag A/B est activé, effacez votre radiotexte actuel.
if radiotext_AB_flag != ((group_1 >> 4) & 0x01):
radiotext = [' ']*65
radiotext_AB_flag = (group_1 >> 4) & 0x01
text_segment_address_code = group_1 & 0x0f
if AB:
radiotext[text_segment_address_code * 2 ] = chr((group_3 >> 8) & 0xff)
radiotext[text_segment_address_code * 2 + 1] = chr(group_3 & 0xff)
else:
radiotext[text_segment_address_code *4 ] = chr((group_2 >> 8) & 0xff)
radiotext[text_segment_address_code * 4 + 1] = chr(group_2 & 0xff)
radiotext[text_segment_address_code * 4 + 2] = chr((group_3 >> 8) & 0xff)
radiotext[text_segment_address_code * 4 + 3] = chr(group_3 & 0xff)
print(''.join(radiotext))
else:
pass
#print("group_type non supporté:", group_type)
L’exemple ci-dessous montre la sortie de l’étape d’analyse syntaxique pour une station FM. Notez comment il doit construire la chaîne de radiotexte sur plusieurs messages, puis il efface périodiquement la chaîne et recommence. Si vous utilisez l’exemple de fichier téléchargé de 1M, vous ne verrez que les premières lignes ci-dessous.
PTY: Top 40
program: 29
coverage_area: Regional 4
ing.
ing. Upb
ing. Upbeat.
ing. Upbeat. Rea
WAY-
WAY-FM U
WAY-FM Uplif
WAY-FM Uplifting
WAY-FM Uplifting. Up
WAY-FM Uplifting. Upbeat
WAY-FM Uplifting. Upbeat. Re
WayF
WayFM Up
WayFM Uplift
WayFM Uplifting.
WayFM Uplifting. Upb
WayFM Uplifting. Upbeat.
WayFM Uplifting. Upbeat. Rea
Récapitulation et code final¶
Vous l’avez fait! Ci-dessous se trouve tout le code ci-dessus, concaténé, il devrait fonctionner avec l’enregistrement radio FM test que vous pouvez trouver ici, bien que vous devriez être en mesure d’alimenter votre propre signal tant que son SNR reçu est assez élevé, il suffit de régler la fréquence centrale de la station et d’échantillonner à un taux de 250 kHz. Si vous trouvez que vous avez dû faire des ajustements pour le faire fonctionner avec votre propre enregistrement ou SDR en direct, faites-moi savoir ce que vous avez dû faire, vous pouvez le soumettre comme un PR GitHub à la page GitHub du manuel. Vous pouvez également trouver une version de ce code avec des dizaines de tracés/graphes de débogage inclus, que j’ai utilisé à l’origine pour faire ce chapitre, ici.
Final Code
import numpy as np
from scipy.signal import resample_poly, firwin, bilinear, lfilter
import matplotlib.pyplot as plt
# Lire le signal
x = np.fromfile('/home/marc/Downloads/fm_rds_250k_1Msamples.iq', dtype=np.complex64)
sample_rate = 250e3
center_freq = 99.5e6
# Démodulation en quadrature
x = 0.5 * np.angle(x[0:-1] * np.conj(x[1:])) # see https://wiki.gnuradio.org/index.php/Quadrature_Demod
# décalage de freq
N = len(x)
f_o = -57e3 # valeur du décalage
t = np.arange(N)/sample_rate # vecteur de temps
x = x * np.exp(2j*np.pi*f_o*t) # décalage de freq
# filtre passe bas
taps = firwin(numtaps=101, cutoff=7.5e3, fs=sample_rate)
x = np.convolve(x, taps, 'valid')
# Décimer par 10, maintenant que nous avons filtré et qu'il n'y aura pas de repliement.
x = x[::10]
sample_rate = 25e3
# Rééchantillonnage à 19 kHz
x = resample_poly(x, 19, 25) # up, down
sample_rate = 19e3
# Filtre passe-bande pour isoler un signal RDS BPSK
taps = firwin(numtaps=501, cutoff=[0.05e3, 2e3], fs=sample_rate, pass_zero=False)
x = np.convolve(x, taps, 'valid')
# Synchronisation des symboles, en utilisant ce que nous avons fait dans le chapitre sur la synchronisation.
samples = x # comme dans le chapitre de la synchronisation
samples_interpolated = resample_poly(samples, 32, 1) # Nous utiliserons 32 comme facteur d'interpolation, choisi arbitrairement.
sps = 16
mu = 0.01 # estimation initiale de la phase de l'échantillon
out = np.zeros(len(samples) + 10, dtype=np.complex64)
out_rail = np.zeros(len(samples) + 10, dtype=np.complex64) # stocke les valeurs, à chaque itération nous avons besoin des 2 valeurs précédentes plus la valeur actuelle.
i_in = 0 # index des échantillons d'entrée
i_out = 2 # indice de sortie (les deux premières sorties sont 0)
while i_out < len(samples) and i_in+32 < len(samples):
out[i_out] = samples_interpolated[i_in*32 + int(mu*32)] # prendre ce que nous pensons être le "meilleur" échantillon
out_rail[i_out] = int(np.real(out[i_out]) > 0) + 1j*int(np.imag(out[i_out]) > 0)
x = (out_rail[i_out] - out_rail[i_out-2]) * np.conj(out[i_out-1])
y = (out[i_out] - out[i_out-2]) * np.conj(out_rail[i_out-1])
mm_val = np.real(y - x)
mu += sps + 0.01*mm_val
i_in += int(np.floor(mu)) # arrondir à l'entier le plus proche puisque nous l'utilisons comme un index
mu = mu - np.floor(mu) # supprimer la partie entière de mu
i_out += 1 # incrémenter l'indice de sortie
x = out[2:i_out] # supprimer les deux premiers, et tout ce qui suit i_out (qui n'a jamais été rempli)
# Synchronisation fine de la fréquence
samples = x # comme dans le chapitre de la synchro
N = len(samples)
phase = 0
freq = 0
# Ces deux paramètres suivants sont ce qu'il faut ajuster, pour rendre la boucle de rétroaction plus rapide ou plus lente (ce qui a un impact sur la stabilité).
alpha = 8.0
beta = 0.002
out = np.zeros(N, dtype=np.complex64)
freq_log = []
for i in range(N):
out[i] = samples[i] * np.exp(-1j*phase) # ajuster l'échantillon d'entrée par l'inverse du décalage de phase estimé
error = np.real(out[i]) * np.imag(out[i]) # Voici la formule d'erreur pour une boucle de Costas de 2ème ordre (par exemple pour BPSK)
# Avancer la boucle (recalculer la phase et le décalage de fréquence)
freq += (beta * error)
freq_log.append(freq * sample_rate / (2*np.pi)) # convertir de la vitesse angulaire en Hz pour les logs
phase += freq + (alpha * error)
# Facultatif : Ajustez la phase pour qu'elle soit toujours comprise entre 0 et 2pi, rappelez-vous que la phase tourne autour 2pi
while phase >= 2*np.pi:
phase -= 2*np.pi
while phase < 0:
phase += 2*np.pi
x = out
# Demodulation BPSK
bits = (np.real(x) > 0).astype(int) # 1s et 0s
# Décodage différentiel, de sorte qu'il importe peu que notre BPSK ait subi une rotation de 180 degrés sans que nous nous en rendions compte.
bits = (bits[1:] - bits[0:-1]) % 2
bits = bits.astype(np.uint8) # decodage
############
# DECODAGE #
############
# Constants
syndrome = [383, 14, 303, 663, 748]
offset_pos = [0, 1, 2, 3, 2]
offset_word = [252, 408, 360, 436, 848]
# regardez Annex B, page 64 du standard
def calc_syndrome(x, mlen):
reg = 0
plen = 10
for ii in range(mlen, 0, -1):
reg = (reg << 1) | ((x >> (ii-1)) & 0x01)
if (reg & (1 << plen)):
reg = reg ^ 0x5B9
for ii in range(plen, 0, -1):
reg = reg << 1
if (reg & (1 << plen)):
reg = reg ^ 0x5B9
return reg & ((1 << plen) - 1) # sélectionner les plen bits de reg les plus bas
# Initialiser toutes les variables de travail dont nous aurons besoin pendant la boucle.
synced = False
presync = False
wrong_blocks_counter = 0
blocks_counter = 0
group_good_blocks_counter = 0
reg = np.uint32(0) # était unsigned long en C++ (64 bits) mais numpy ne supporte pas les opérations bit à bit de uint64, je ne pense pas qu'il atteigne cette valeur de toute façon.
lastseen_offset_counter = 0
lastseen_offset = 0
# le processus de synchronisation est décrit dans l'annexe C, page 66 de la norme */
bytes_out = []
for i in range(len(bits)):
# en C++, reg n'est pas initié, il sera donc aléatoire au début, pour le nôtre, il s'agit de 0.
# C'était aussi un unsigned long mais il ne semblait pas s'approcher de la valeur maximale.
# les bits sont soit 0 soit 1
reg = np.bitwise_or(np.left_shift(reg, 1), bits[i]) # reg contient les 26 derniers bits de RDS. Ce sont tous deux des opérations par bit.
if not synced:
reg_syndrome = calc_syndrome(reg, 26)
for j in range(5):
if reg_syndrome == syndrome[j]:
if not presync:
lastseen_offset = j
lastseen_offset_counter = i
presync = True
else:
if offset_pos[lastseen_offset] >= offset_pos[j]:
block_distance = offset_pos[j] + 4 - offset_pos[lastseen_offset]
else:
block_distance = offset_pos[j] - offset_pos[lastseen_offset]
if (block_distance*26) != (i - lastseen_offset_counter):
presync = False
else:
print('Etat de la synchronisation détecté')
wrong_blocks_counter = 0
blocks_counter = 0
block_bit_counter = 0
block_number = (j + 1) % 4
group_assembly_started = False
synced = True
break # syndrome trouvé, plus de cycles
else: # SYNCHRONISÉ
# attendre que 26 bits entrent dans le tampon */
if block_bit_counter < 25:
block_bit_counter += 1
else:
good_block = False
dataword = (reg >> 10) & 0xffff
block_calculated_crc = calc_syndrome(dataword, 16)
checkword = reg & 0x3ff
if block_number == 2: # gérer le cas particulier du mot de décalage C ou C'.
block_received_crc = checkword ^ offset_word[block_number]
if (block_received_crc == block_calculated_crc):
good_block = True
else:
block_received_crc = checkword ^ offset_word[4]
if (block_received_crc == block_calculated_crc):
good_block = True
else:
wrong_blocks_counter += 1
good_block = False
else:
block_received_crc = checkword ^ offset_word[block_number] # xor binaire
if block_received_crc == block_calculated_crc:
good_block = True
else:
wrong_blocks_counter += 1
good_block = False
# Vérification du CRC terminée
if block_number == 0 and good_block:
group_assembly_started = True
group_good_blocks_counter = 1
group = bytearray(8) # 8 octets remplis de 0
if group_assembly_started:
if not good_block:
group_assembly_started = False
else:
# octets de données brutes, tels que reçus du RDS. 8 octets d'information, suivis de 4 caractères de décalage RDS : ABCD/ABcD/EEEE (aux Etats-Unis) que nous laissons de côté ici.
# Mots d'information RDS
# le numéro de bloc est soit 0,1,2,3 donc c'est comme ça qu'on remplit les 8 octets
group[block_number*2] = (dataword >> 8) & 255
group[block_number*2+1] = dataword & 255
group_good_blocks_counter += 1
#print('group_good_blocks_counter:', group_good_blocks_counter)
if group_good_blocks_counter == 5:
#print(group)
bytes_out.append(group) # liste de listes d'octets de longueur 8
block_bit_counter = 0
block_number = (block_number + 1) % 4
blocks_counter += 1
if blocks_counter == 50:
if wrong_blocks_counter > 35: # Autant de blocs erronés doivent signifier que nous avons perdu la synchronisation.
print("Perte de synchronisation (obtient ", wrong_blocks_counter, " mauvais blocs sur ", blocks_counter, " en total)")
synced = False
presync = False
else:
print("Toujours synchronisé (obtient ", wrong_blocks_counter, " mauvais blocs sur ", blocks_counter, " en total)")
blocks_counter = 0
wrong_blocks_counter = 0
############
# Analyse #
############
# Annexe F de la norme RBDS Tableau F.1 (Amérique du Nord) et Tableau F.2 (Europe)
# Europe Amérique du Nord
pty_table = [["Undefined", "Undefined"],
["News", "News"],
["Current Affairs", "Information"],
["Information", "Sports"],
["Sport", "Talk"],
["Education", "Rock"],
["Drama", "Classic Rock"],
["Culture", "Adult Hits"],
["Science", "Soft Rock"],
["Varied", "Top 40"],
["Pop Music", "Country"],
["Rock Music", "Oldies"],
["Easy Listening", "Soft"],
["Light Classical", "Nostalgia"],
["Serious Classical", "Jazz"],
["Other Music", "Classical"],
["Weather", "Rhythm & Blues"],
["Finance", "Soft Rhythm & Blues"],
["Children’s Programmes", "Language"],
["Social Affairs", "Religious Music"],
["Religion", "Religious Talk"],
["Phone-In", "Personality"],
["Travel", "Public"],
["Leisure", "College"],
["Jazz Music", "Spanish Talk"],
["Country Music", "Spanish Music"],
["National Music", "Hip Hop"],
["Oldies Music", "Unassigned"],
["Folk Music", "Unassigned"],
["Documentary", "Weather"],
["Alarm Test", "Emergency Test"],
["Alarm", "Emergency"]]
pty_locale = 1 # mis à 0 pour l'Europe qui utilisera la première colonne à la place.
# page 72, Annex D, table D.2 in the standard
coverage_area_codes = ["Local",
"International",
"National",
"Supra-regional",
"Regional 1",
"Regional 2",
"Regional 3",
"Regional 4",
"Regional 5",
"Regional 6",
"Regional 7",
"Regional 8",
"Regional 9",
"Regional 10",
"Regional 11",
"Regional 12"]
radiotext_AB_flag = 0
radiotext = [' ']*65
first_time = True
for group in bytes_out:
group_0 = group[1] | (group[0] << 8)
group_1 = group[3] | (group[2] << 8)
group_2 = group[5] | (group[4] << 8)
group_3 = group[7] | (group[6] << 8)
group_type = (group_1 >> 12) & 0xf # voici ce que chacun signifie, par exemple RT est radiotexte qui est le seul que nous décodons ici : ["BASIC", "PIN/SL", "RT", "AID", "CT", "TDC", "IH", "RP", "TMC", "EWS", "___", "___", "___", "___", "EON", "___"]
AB = (group_1 >> 11 ) & 0x1 # b si 1, a si 0
#print("group_type:", group_type) # il s'agit essentiellement du type de message, je ne vois que les types 0 et 2 dans mon enregistrement.
#print("AB:", AB)
program_identification = group_0 # "PI"
program_type = (group_1 >> 5) & 0x1f # "PTY"
pty = pty_table[program_type][pty_locale]
pi_area_coverage = (program_identification >> 8) & 0xf
coverage_area = coverage_area_codes[pi_area_coverage]
pi_program_reference_number = program_identification & 0xff # juste un entier
if first_time:
print("PTY:", pty)
print("program:", pi_program_reference_number)
print("coverage_area:", coverage_area)
first_time = False
if group_type == 2:
# lorsque le flag A/B est activé, effacez votre radiotexte actuel.
if radiotext_AB_flag != ((group_1 >> 4) & 0x01):
radiotext = [' ']*65
radiotext_AB_flag = (group_1 >> 4) & 0x01
text_segment_address_code = group_1 & 0x0f
if AB:
radiotext[text_segment_address_code * 2 ] = chr((group_3 >> 8) & 0xff)
radiotext[text_segment_address_code * 2 + 1] = chr(group_3 & 0xff)
else:
radiotext[text_segment_address_code *4 ] = chr((group_2 >> 8) & 0xff)
radiotext[text_segment_address_code * 4 + 1] = chr(group_2 & 0xff)
radiotext[text_segment_address_code * 4 + 2] = chr((group_3 >> 8) & 0xff)
radiotext[text_segment_address_code * 4 + 3] = chr(group_3 & 0xff)
print(''.join(radiotext))
else:
pass
#print("group_type non supporté:", group_type)
Encore une fois, l’exemple d’enregistrement FM connu pour fonctionner avec ce code peut être trouvé ici.
Pour ceux qui sont intéressés par la démodulation du signal audio réel, il suffit d’ajouter les lignes suivantes juste après (merci à Joel Cordeiro pour le code):
# Ajoutez le code suivant juste après la section acquisition d'un signal.
from scipy.io import wavfile
# Demodulation
x = np.diff(np.unwrap(np.angle(x)))
# Filtre de désaccentuation (de-emphasis), H(s) = 1/(RC*s + 1), implémenté comme un IIR via une transformation bilinéaire
bz, az = bilinear(1, [75e-6, 1], fs=sample_rate)
x = lfilter(bz, az, x)
# filtre de décimation pour obtenir un son mono
x = x[::6]
sample_rate = sample_rate/6
# normaliser le volume
x /= x.std()
# Enregistrez dans un fichier wav, vous pouvez l'ouvrir dans Audacity par exemple.
wavfile.write('fm.wav', int(sample_rate), x)
La partie la plus compliquée est le filtre de désaccentuation (ou de-emphasis), que vous pouvez apprendre ici, bien qu’il s’agisse en fait d’une étape optionnelle si vous pouvre vous suffir d’un audio qui a un mauvais équilibre entre les basses et les aigus. Pour les curieux, voici à quoi ressemble la réponse en fréquence de ce filtre IIR, il ne filtre pas complètement les fréquences, c’est plus un filtre de “mise en forme”.
Remerciements¶
La plupart des étapes ci-dessus utilisées pour recevoir le RDS ont été adaptées de l’implémentation GNU Radio du RDS, qui est dans le module GNU Radio appelé gr-rds, créé à l’origine par Dimitrios Symeonidis et maintenu par Bastian Bloessl, et je voudrais remercier le travail de ces auteurs. Afin de créer ce chapitre, j’ai commencé par utiliser gr-rds dans GNU Radio, avec un enregistrement FM fonctionnel, et j’ai converti pas-à-pas chacun des blocs (y compris de nombreux blocs intégrés) en Python. Cela a pris pas mal de temps, il y a des nuances dans les blocs intégrés qui sont faciles à rater, et passer d’un traitement de signal de type stream (c’est-à-dire utilisant une fonction de travail qui traite quelques milliers d’échantillons à la fois) à un bloc de Python n’a pas été toujours simple. GNU Radio est un outil extraordinaire pour ce type de prototypage et je n’aurais jamais pu créer tout ce code Python fonctionnel sans lui.
