8. Filters¶

Dit hoofdstuk gaan we digitale filters in Python behandelen. We zullen de typen filters behandelen (FIR/IIR en laagdoorlaat/hoogdoorlaat/banddoorlaat/bandstop), hoe ze digitaal eruitzien, en hoe ze ontworpen worden. Als laatste zullen we eindigen met een introductie over ‘pulse shaping’ (Nederlands: pulsvorming), wat in het Pulse Shaping hoofdstuk zal worden uitgediept.

8.1. Basis van Filters¶

Veel disciplines maken gebruik van filters. Beeldverwerking maakt bijvoorbeeld uitvoerig gebruik van 2D filters waarbij de in- en uitgangen figuren betreft. Wellicht gebruik je elke morgen een koffiefilter om de vaste en vloeibare stoffen te scheiden. In digitale signaalbewerking worden filters voornamelijk toegepast voor het:

Scheiden van gecombineerde signalen (dus het gewenste signaal extraheren)
Verwijderen van overbodige ruis na ontvangst van een signaal
Herstellen van signalen die zijn vervormd (een audio equalizer is bijv. een filter)

Natuurlijk zijn er nog meer toepassingen, maar de bedoeling van dit hoofdstuk is om het concept te introduceren in plaats van alle filtertoepassingen.

Misschien denk je dat we alleen geïnteresseerd zijn in digitale filters; het is ten slotte een DSP boek. Het is echter belangrijk om te begrijpen dat veel filters analoog zullen zijn, zoals de filters die in jouw SDR voor de ADC’s zijn gezet. Het volgende figuur plaatst een schema van een analoog filter tegenover het schematisch ontwerp van een digitaal filter.

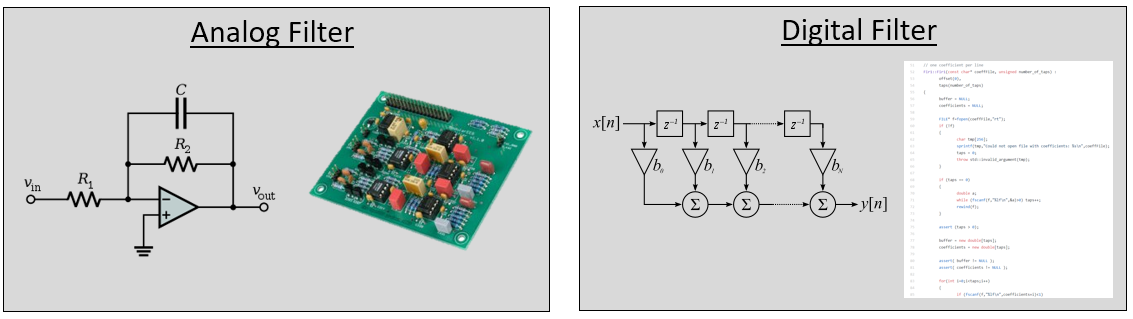
DSP’s hebben signalen als in- en uitgangen. Een filter heeft een ingangssignaal en een uitgangssignaal:

Je kunt niet twee verschillende signalen in een enkel filter stoppen zonder ze eerst samen te voegen of een andere operatie uit te voeren. Op dezelfde manier zal de uitgang altijd een signaal betreffen, bijv. een 1D array van getallen.

Er zijn vier basistypen filters: laagdoorlaat, hoogdoorlaat, banddoorlaat en bandstop (of sper). Elke type bewerkt signalen zodanig dat de focus op verschillende gebieden aan frequenties ligt. De onderstaande grafieken laten voor elk van de typen zien hoe de frequenties worden gefilterd. Eerst worden, voor de duidelijkheid, alleen de positieve frequenties getoond, daarna ook figuren met negatieve frequenties. Zolang de filters “reëel” zijn, zullen de filters gespiegeld zijn rondom 0 Hz.

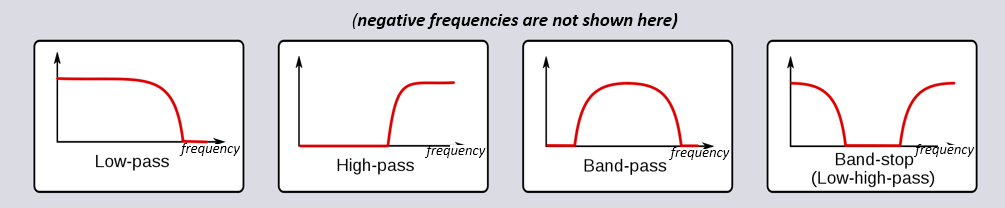
Inclusief negatieve frequenties:

Elk filter laat bepaalde frequenties in een signaal door, terwijl het andere frequenties blokkeert. Het bereik aan frequenties wat wordt doorgelaten heet de “doorlaatband”, en wat wordt geblokkeerd heet de “stopband”. In het geval van een laagdoorlaatfilter worden lage frequenties doorgelaten en hoge frequenties geblokkeerd, dus 0Hz zal altijd in de doorlaatband vallen. Bij hoog- en banddoorlaatfilters bevindt 0 Hz zich altijd in de stopband.

Verwar deze filtertypes niet met de implementatietypes (dus IIR en FIR). Omdat we regelmatig signalen in de basisband gebruiken, wordt het laag-doorlaat filter (LPF) veruit het meeste gebruikt. Een LPF staat ons toe om alles “rond” ons signaal, zoals ruis en andere signalen, weg te filteren.

8.2. Filteropbouw¶

De meeste digitale filters die we tegen zullen komen (zoals FIR) kunnen we beschrijven met een array van floating point getallen. Filters die in het frequentiedomein symmetrisch zijn, bestaan uit (meestal een oneven aantal) reële getallen (i.p.v. complex). We noemen deze array van getallen “coëfficiënten” of in het Engels “taps”. Meestal gebruiken we $h$ als symbool voor deze filter coëfficiënten/taps. Hier zijn een aantal voorbeeldcoëfficiënten van een enkel filter:

h =  [ 9.92977939e-04  1.08410297e-03  8.51595307e-04  1.64604862e-04
 -1.01714338e-03 -2.46268845e-03 -3.58236429e-03 -3.55412543e-03
 -1.68583512e-03  2.10562324e-03  6.93100252e-03  1.09302641e-02
  1.17766532e-02  7.60955496e-03 -1.90555639e-03 -1.48306750e-02
 -2.69313236e-02 -3.25659606e-02 -2.63400086e-02 -5.04184562e-03
  3.08099470e-02  7.64264738e-02  1.23536693e-01  1.62377258e-01
  1.84320776e-01  1.84320776e-01  1.62377258e-01  1.23536693e-01
  7.64264738e-02  3.08099470e-02 -5.04184562e-03 -2.63400086e-02
 -3.25659606e-02 -2.69313236e-02 -1.48306750e-02 -1.90555639e-03
  7.60955496e-03  1.17766532e-02  1.09302641e-02  6.93100252e-03
  2.10562324e-03 -1.68583512e-03 -3.55412543e-03 -3.58236429e-03
 -2.46268845e-03 -1.01714338e-03  1.64604862e-04  8.51595307e-04
  1.08410297e-03  9.92977939e-04]

Voorbeeldtoepassing¶

Om te leren hoe onze filters worden gebruikt gaan we kijken naar een voorbeeld waarin we onze SDR op een frequentie van een bestaand signaal afstemmen. Rondom dat signaal zijn andere signalen die we weg willen halen. Vergeet niet dat, terwijl we onze SDR op een radiofrequentie afstemmen, de samples die de SDR teruggeeft in de basisband zitten. Dit betekent dat het signaal dus gecentreerd zal zijn rond de 0 Hz. We moeten zelf onthouden op welke frequentie we de SDR hadden ingesteld. Dit zouden we dan kunnen ontvangen:

GNU Radio frequency domain plot of signal of interest and an interfering signal and noise floor

We weten dat we een laagdoorlaatfilter nodig hebben omdat ons signaal al rond DC (0 Hz) is gecentreerd. We moeten de “kantelfrequentie” (Engels “cutoff”) kiezen waar de doorlaatband overgaat in de stopband. De kantelfrequentie wordt altijd in Hz gegeven. In dit voorbeeld lijkt 3 kHz wel een goede waarde:

Maar, gezien hoe de meeste laagdoorlaatfilters werken, zal de negatieve kantelfrequentie ook op (-)3 kHz liggen. Het is dus symmetrisch rond DC (later zien we waarom). Onze kantelfrequenties zien er dan ongeveer zo uit (de doorlaatband ligt tussen):

Na het maken en toepassen van een filter met een kantelfrequentie van 3 kHz krijgen we:

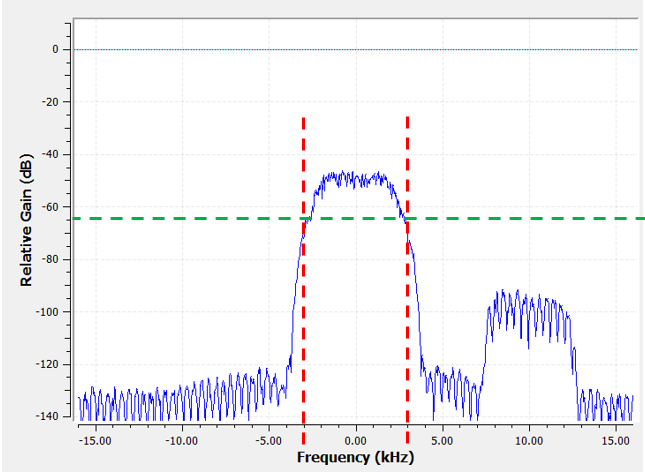
GNU Radio frequency domain plot of signal of interest and an interfering signal and noise floor, with interference filtered out

Dit gefilterde signaal ziet er misschien verwarrend uit totdat je beseft dat de ruisvloer rond de groene lijn zat op -70 dB. Ook al zien we het signaal rond de 10 kHz nog steeds, het is sterk in vermogen afgenomen. Het is zelfs zwakker geworden dan de oude ruisvloer! Daarnaast hebben we dus ook de meeste ruis in de stopband verwijderd.

Een andere belangrijke instelling van ons laagdoorlaatfilter, naast de kantelfrequentie, is de transitiebreedte (Engels: “Transition width”). Dit wordt uitgedrukt in Hz en vertelt het filter hoe snel het moet overgaan van de doorlaatband naar de stopband, want een directe overgang is onmogelijk.

Laten we de transitiebreedte bekijken. In het onderstaande figuur laat de groene lijn de ideale filterrespons zien met een transitiebreedte van 0 Hz. De rode lijn laat een realistisch filter zien, met een golvend gedrag in de doorlaat- en stopband en met een bepaalde transitiebreedte. De frequentie in dit figuur is genormaliseerd met de sample-frequentie.

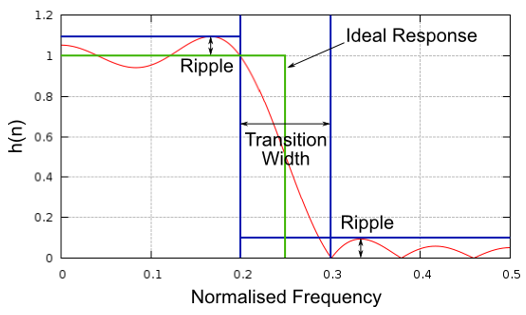
Frequency response of a low-pass filter, showing ripple and transition width

Nu vraag je je misschien af waarom we niet gewoon een zo’n kleine transitiebreedte als mogelijk kiezen. De voornaamste reden is dat een kleinere breedte tot meer coëfficiënten zal leiden, en hoe meer coëfficiënten hoe intensiever het wordt om te berekenen. Een filter met 50 coëfficiënten kan heel de dag draaien en de CPU nog geen 1% belasten op een RaspberryPi, terwijl een filter met 50000 coëfficiënten de CPU doet ontploffen! Meestal gebruiken we een filterontwerpprogramma om te zien over hoe veel coëfficiënten het gaat. Als dit veel te veel is (bijv. meer dan 100) dan verbreden we de transitie. Natuurlijk hangt dit allemaal af van de toepassing en de hardware waarop het filter draait.

In het filtervoorbeeld hierboven hebben we een kantelfrequentie van 3 kHz en een transitiebreedte van 1 kHz gebruikt. Het resulterende filter gebruikte 77 coëfficiënten.

Terug naar filteropbouw. Ook al gebruiken we een lijst van coëfficiënten voor een filter, meestal visualiseren we een filter in het frequentiedomein. Dit wordt de frequentierespons van het filter genoemd en laat het gedrag in frequentie zien. Hier is de frequentierespons van het filter dat we zojuist gebruikten:

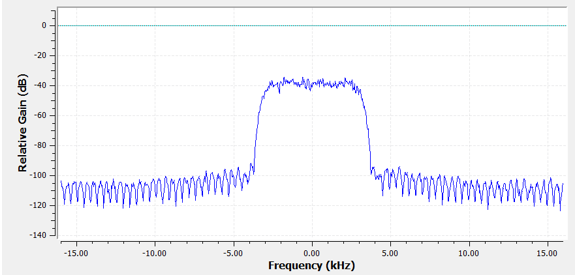
Let op dat wat hier getoond wordt niet een signaal is, het is de frequentierespons van het filter. Misschien is het moeilijk om je vinger hier op te leggen, terwijl we voorbeelden en programma’s bekijken zal het duidelijker worden.

Een filter heeft ook een tijddomein-versie; dit heet de “impulsrespons” van het filter. Dit heet zo omdat een impuls aan de ingang deze respons aan de uitgang geeft. Google de “dirac delta functie” voor meer informatie over zo’n impuls. Voor een geven FIR-filter is de impulsrespons gelijk aan de coëfficiënten zelf. Voor dat filter met 77 coëfficiënten van eerder is dat:

h =  [-0.00025604525581002235, 0.00013669139298144728, 0.0005385575350373983,
0.0008378280326724052, 0.000906112720258534, 0.0006353431381285191,
-9.884083502996931e-19, -0.0008822851814329624, -0.0017323142383247614,
-0.0021665366366505623, -0.0018335371278226376, -0.0005912294145673513,
0.001349081052467227, 0.0033936649560928345, 0.004703888203948736,
0.004488115198910236, 0.0023609865456819534, -0.0013707970501855016,
-0.00564080523326993, -0.008859002031385899, -0.009428252466022968,
-0.006394983734935522, 4.76480351940553e-18, 0.008114570751786232,
0.015200719237327576, 0.018197273835539818, 0.01482443418353796,
0.004636279307305813, -0.010356673039495945, -0.025791890919208527,
-0.03587324544787407, -0.034922562539577484, -0.019146423786878586,
0.011919975280761719, 0.05478153005242348, 0.10243935883045197,
0.1458890736103058, 0.1762896478176117, 0.18720689415931702,
0.1762896478176117, 0.1458890736103058, 0.10243935883045197,
0.05478153005242348, 0.011919975280761719, -0.019146423786878586,
-0.034922562539577484, -0.03587324544787407, -0.025791890919208527,
-0.010356673039495945, 0.004636279307305813, 0.01482443418353796,
0.018197273835539818, 0.015200719237327576, 0.008114570751786232,
4.76480351940553e-18, -0.006394983734935522, -0.009428252466022968,
-0.008859002031385899, -0.00564080523326993, -0.0013707970501855016,
0.0023609865456819534, 0.004488115198910236, 0.004703888203948736,
0.0033936649560928345, 0.001349081052467227, -0.0005912294145673513,
-0.0018335371278226376, -0.0021665366366505623, -0.0017323142383247614,
-0.0008822851814329624, -9.884083502996931e-19, 0.0006353431381285191,
0.000906112720258534, 0.0008378280326724052, 0.0005385575350373983,
0.00013669139298144728, -0.00025604525581002235]

Ook al hebben we nog niets geleerd over filterontwerp, hieronder kun je de code van dat filter vinden:

import numpy as np
from scipy import signal
import matplotlib.pyplot as plt

num_taps = 51 # aantal coëfficiënten
cut_off = 3000 # kantelfrequentie in Hz
sample_rate = 32000 # Hz

# laag-doorlaatfilter
h = signal.firwin(num_taps, cut_off, fs=sample_rate)

# impulsrespons weergeven
plt.plot(h, '.-')
plt.show()

Wanneer we deze coëfficiënten in de tijd weergeven dan krijgen we de impulsrespons:

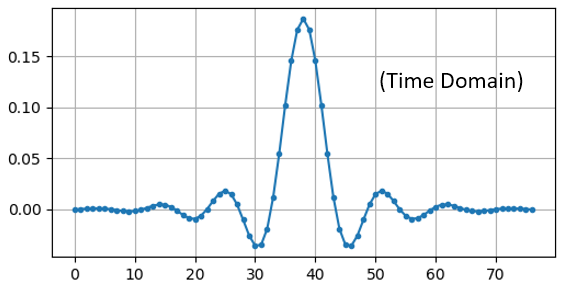
Example of impulse response of a filter, plotting the taps in the time domain

De code om de frequentierespons van eerder te genereren wordt hieronder getoond. Dit is iets ingewikkelder omdat we een x-as voor de frequenties moeten opzetten.

# Frequentierespons
H = np.abs(np.fft.fft(h, 1024)) # neem een 1024-punten FFT met modulus
H = np.fft.fftshift(H) # frequenties op juiste plek zetten
w = np.linspace(-sample_rate/2, sample_rate/2, len(H)) # x-as
plt.plot(w, H, '.-')
plt.show()

Reële versus Complexe filters¶

Voor zover hebben de filters reële coëfficiënten, maar de coëfficiënten kunnen ook complex zijn. Of de coëfficiënten reëel of complex zijn heeft niets te maken met de ingang, je kunt een reëel signaal in een complex filter stoppen en andersom. Wanneer de coëfficiënten reëel zijn dan is de frequentierespons symmetrisch rondom DC (0Hz). We gebruiken complexe coëfficiënten alleen wanneer we een asymmetrisch filter willen, wat niet vaak het geval is.

Als een voorbeeld voor complexe coëfficiënten nemen we het eerdere spectrum, maar deze keer zullen we het andere signaal proberen te ontvangen zonder de SDR opnieuw in te stellen. Dit betekent dat we een (niet symmetrisch) banddoorlaatfilter willen gebruiken. We willen alleen de frequenties rond 7 tot 13 kHz gebruiken, maar niet de frequenties van -13 tot -7 kHz:

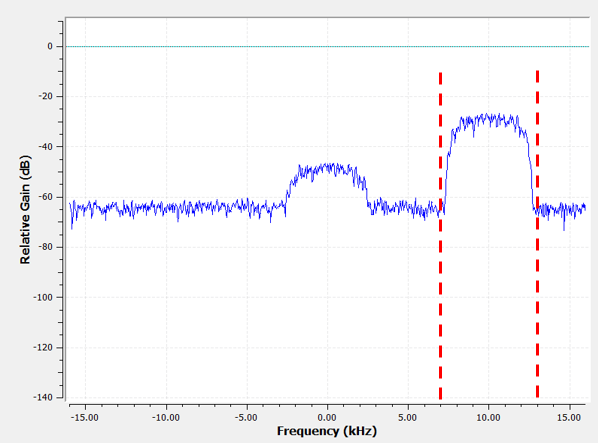
Een manier om dit filter te maken is om een laagdoorlaatfilter met een kantelfrequentie van 3 kHz te nemen en daarna in frequentie op te schuiven. We kunnen een frequentieverschuiving aan x(t) (tijddomein) geven door het te vermenigvuldigen met $e^{j2\pi f_0t}$ . In dit geval moet $f_0$ dan 10 kHz zijn wat het filter 10 kHz zou opschuiven. In het bovenstaande voorbeeld beschreef $h$ de coëfficiënten van het laagdoorlaatfilter. Dus om ons banddoorlaatfilter te maken zullen we de coëfficiënten (de impulsrespons) met $e^{j2\pi f_0t}$ moeten vermenigvuldigen, dit houdt in dat we aan elk sample (coëfficiënt) de juiste tijd moeten koppelen (de inverse van onze sample-frequentie):

# (h staat in eerder gegeven code)

# Verschuif het filter in frequentie door te vermenigvuldigen met exp(j*2*pi*f0*t)
f0 = 10e3 # we verschuiven 10k
Ts = 1.0/sample_rate # sample-frequentie
t = np.arange(0.0, Ts*len(h), Ts) # vector met tijden van samples. (start, stop, stap)
exponential = np.exp(2j*np.pi*f0*t) # dit is een complexe sinus

h_band_pass = h * exponential # verschuiving uitvoeren

# impulsrespons weergeven
plt.figure('impulse')
plt.plot(np.real(h_band_pass), '.-')
plt.plot(np.imag(h_band_pass), '.-')
plt.legend(['real', 'imag'], loc=1)

# frequentierespons weergeven
H = np.abs(np.fft.fft(h_band_pass, 1024)) # 1024-punts FFT met modulus
H = np.fft.fftshift(H) # frequenties op juiste plek zetten
w = np.linspace(-sample_rate/2, sample_rate/2, len(H)) # x-as
plt.figure('freq')
plt.plot(w, H, '.-')
plt.xlabel('Frequency [Hz]')
plt.show()

De impuls- en frequentierespons worden hieronder weergeven:

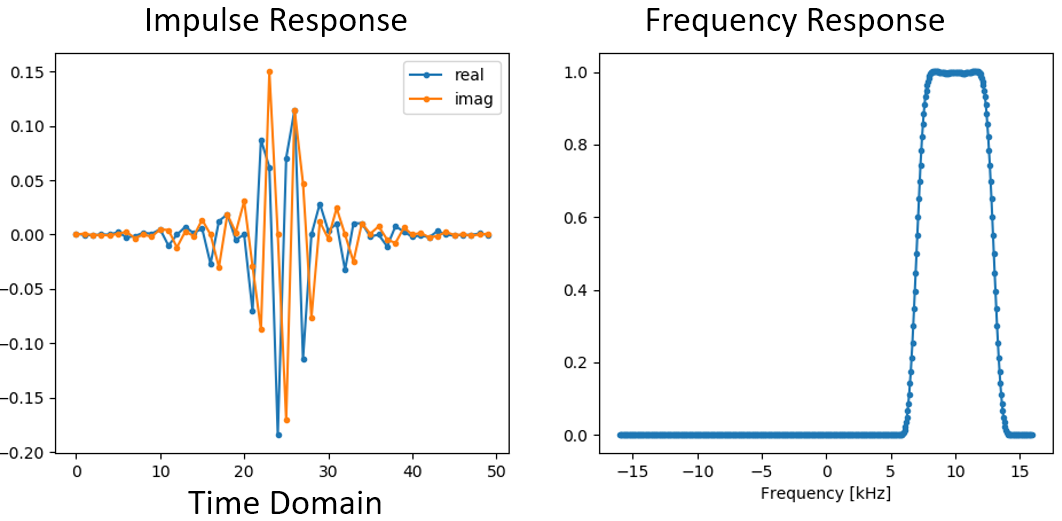
Omdat ons filter niet symmetrisch is rond de 0 Hz, moeten we complexe coëfficiënten gebruiken en hebben we twee lijnen nodig om het te weergeven. Deze complexe impulsrespons is aan de linkerkant van het bovenstaande figuur te zien. De rechterkant valideert dat we inderdaad het gewenste filter hebben verkregen; het filtert alles weg, behalve de frequenties rondom 10 kHz. Let nogmaals op dat het bovenstaande figuur geen signaal is, maar de respons van het filter. Dit kan lastig zijn om te vatten want we passen het filter toe op een signaal en geven de uitgang weer in het frequentiedomein, wat in veel gevallen bijna met de frequentierespons van het filter overeenkomt.

Maak je geen zorgen als dit stuk nog meer verwarring heeft veroorzaakt, 99% van de tijd gebruiken we alleen laagdoorlaatfilters met reële coëfficiënten.

8.3. Convolutie¶

We nemen een korte omleiding om de convolutie operatie te introduceren. Voel je vrij deze sectie over te slaan als je er al bekend mee bent.

Een manier om twee signalen samen te voegen is door ze op te tellen. In het Het Frequentiedomein hoofdstuk hebben we ontdekt hoe lineariteit geldt wanneer we twee signalen optellen. Convolutie is een andere manier om twee signalen te combineren, maar het is compleet anders dan optellen. Convolutie van twee signalen is alsof je ze over elkaar schuift en dan integreert. Het lijkt enorm op kruiscorrelatie, als je daar bekend mee bent. Het is in veel gevallen eigenlijk hetzelfde als kruiscorrelatie. Meestal gebruiken we het * symbool om convolutie aan te geven.

Ik ben overtuigd dat je convolutie het beste leert met hulp van voorbeelden. In dit eerste voorbeeld convolueren we twee blokgolven met elkaar.

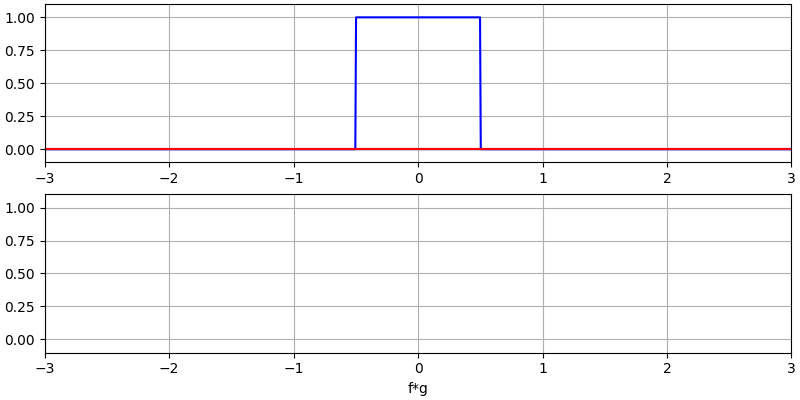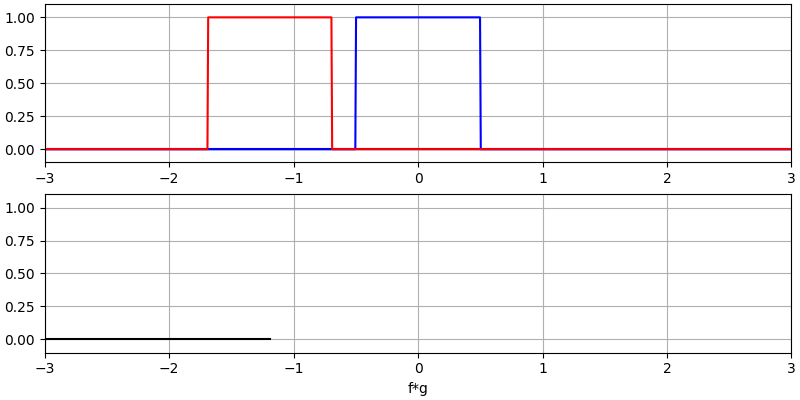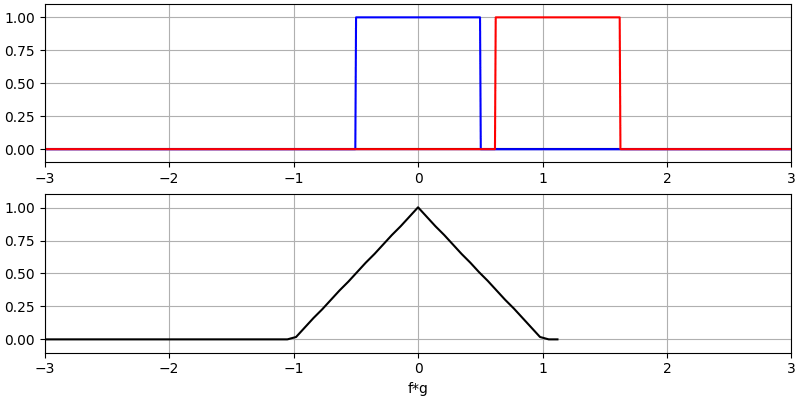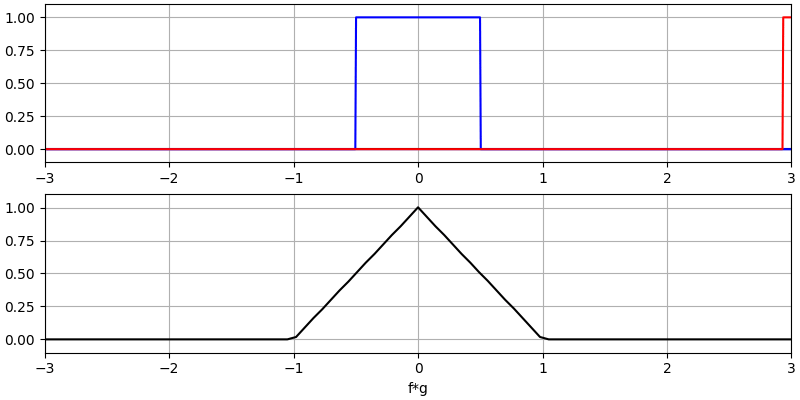
Er zijn twee ingangssignalen (een rode en een blauwe) en de uitgang van de convolutie is in het zwart weergegeven. Je kunt zien dat de uitgang gelijk is aan de integratie van de twee signalen terwijl ze over elkaar schuiven. Omdat het gewoon schuivende integratie is, is het resultaat een driehoek met zijn maximum op het punt waar de twee golven perfect overlappen.

Laten we nog een paar convoluties bekijken:

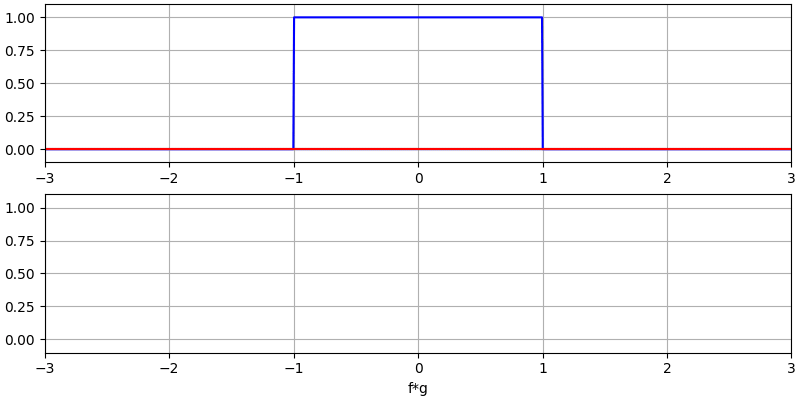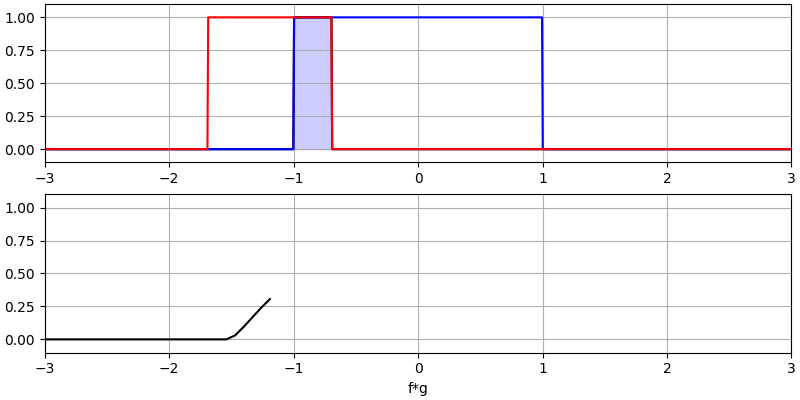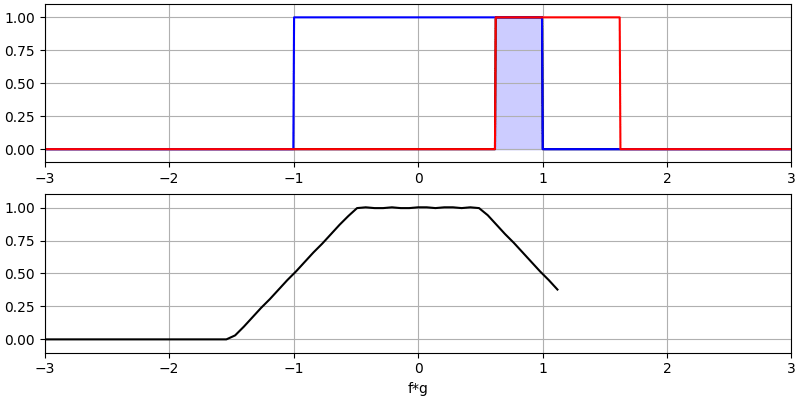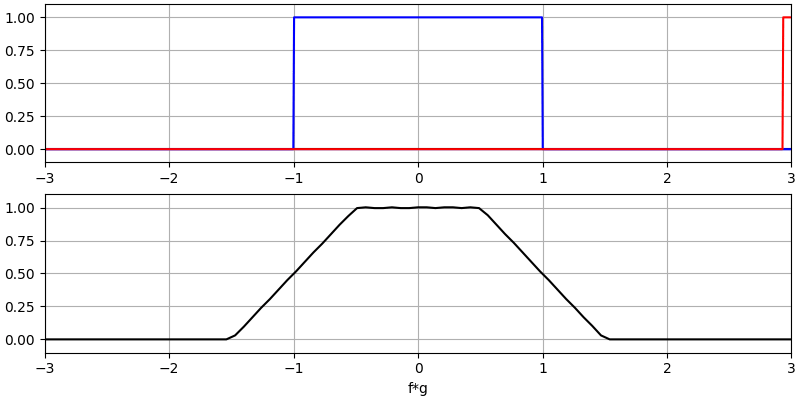
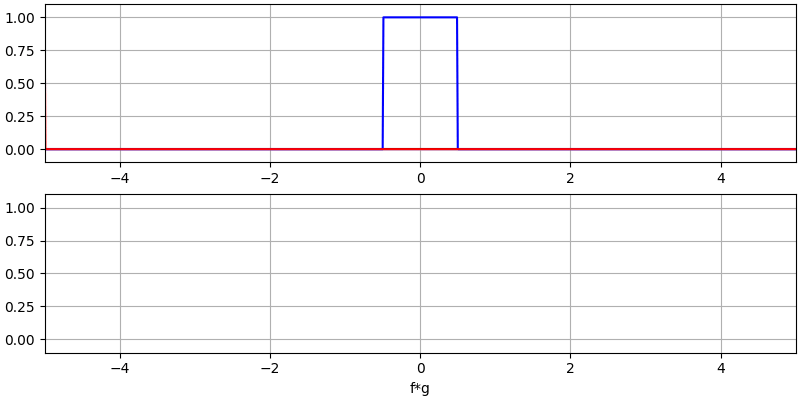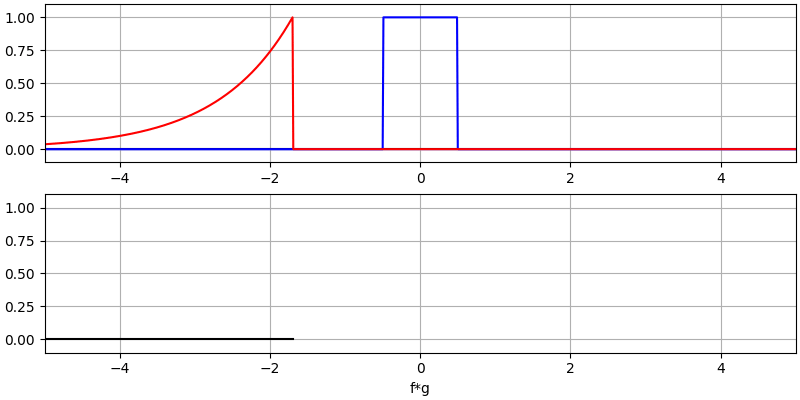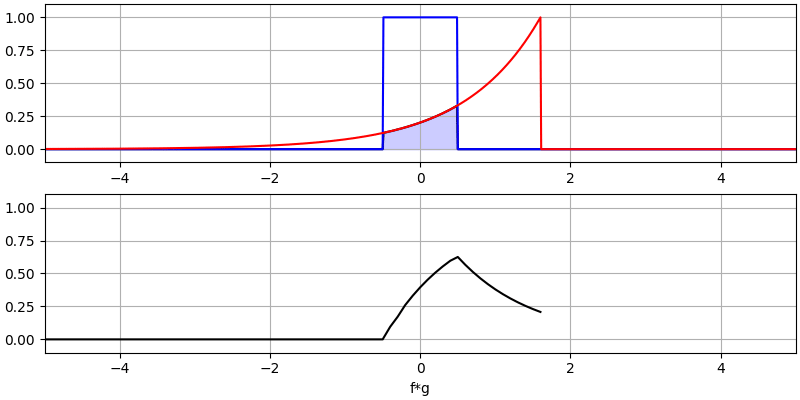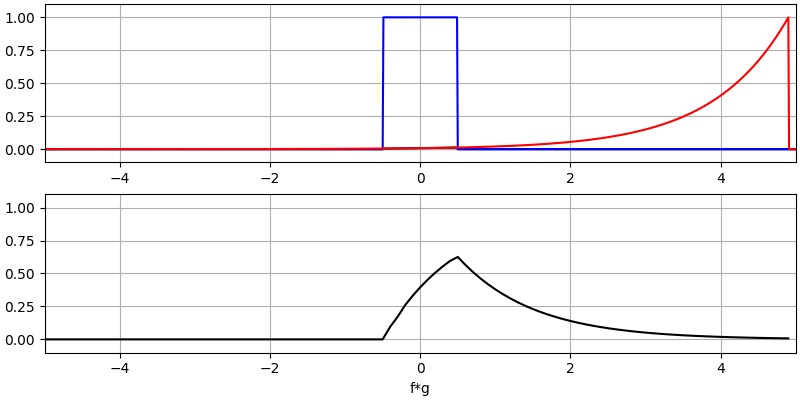
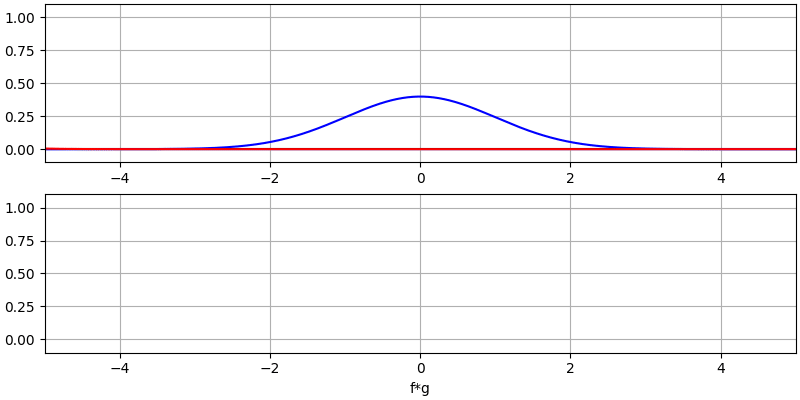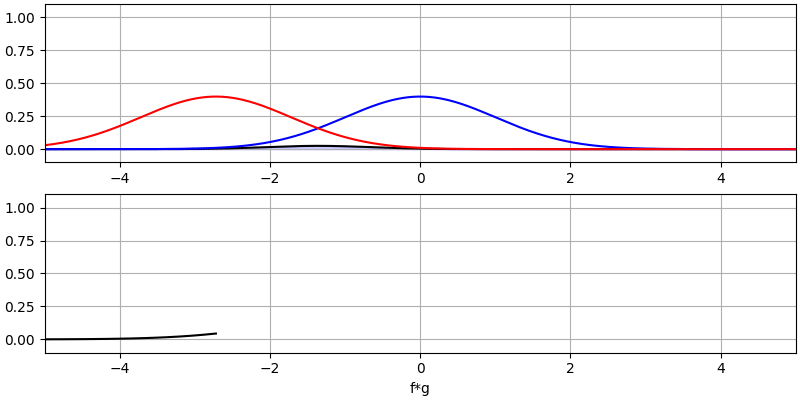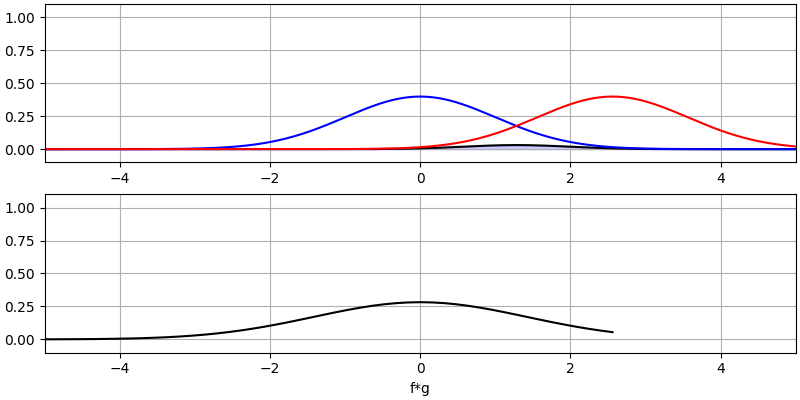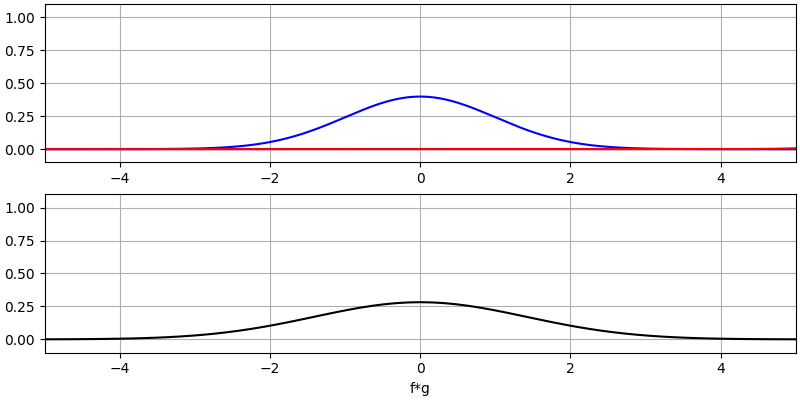
Het convolueren van een Gaussische puls met een Gaussische puls geeft een Gaussische puls, maar breder en een lagere amplitude.

Vanwege dit geschuif is de lengte van de uitgang groter dan de ingang. Als het ene signaal M samples heeft en het ander signaal N samples, dan geeft de convolutie van de twee signalen N+M-1 samples. Desalniettemin hebben functies zoals numpy.convolve() een manier om aan te geven of je de volledige uitgang (max(M, N) samples) wilt hebben, of alleen de samples waar de signalen overlapten(max(M, N) - min(M, N) + 1 als je nieuwsgierig was). Geen reden om in deze details verstrikt te raken. Probeer hieruit op te pikken dat de uitgang van een convolutie niet de lengte heeft van de ingangen.

En waarom is convolutie interessant in digitale signaalbewerking? Om te beginnen, om een signaal te filteren, kunnen we simpelweg de impulsrespons van het filter nemen en convolueren met het signaal. Een FIR-filter voert dus convolutie uit.

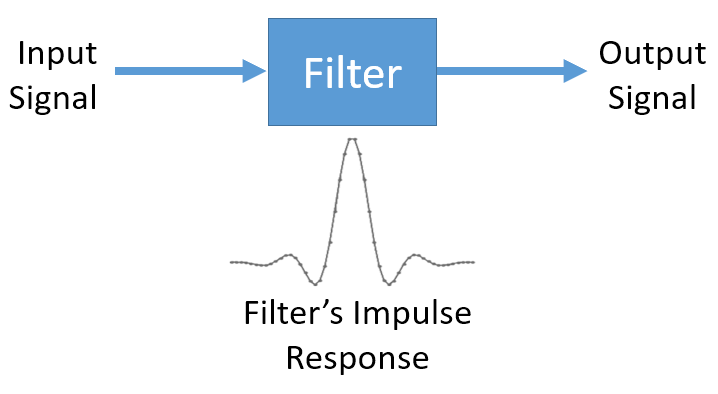
Dit is misschien verwarrend gezien we eerder zeiden dat convolutie twee ingangen en een uitgang heeft. De convolutie voert een wiskundige actie uit op twee 1D arrays. Een van die 1D arrays is de impulsrespons van het filter, de andere 1D array kan een stuk van het ingangssignaal zijn, en de uitgang is dan de gefilterde versie van de ingang.

Laten we naar nog een voorbeeld kijken om dit duidelijk te maken. In het onderstaande voorbeeld stelt de driehoek de impulsrespons van ons filter voor. Het groene signaal is het signaal wat gefilterd wordt.

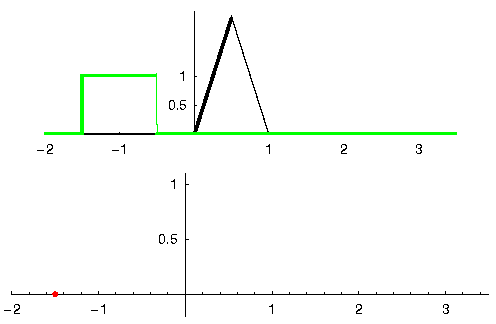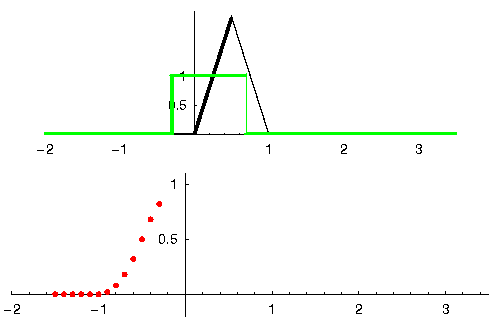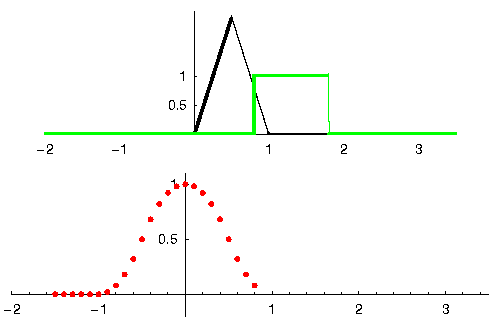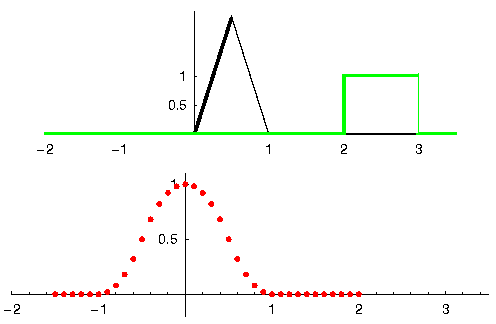
De rode uitgang is het gefilterde signaal.

Vraag: wat voor type filter was de driehoek?

Antwoord:

Het heeft de hoge frequentiecomponenten van het groene signaal gladgestreken (de scherpe overgangen van het vierkant) dus het gedraagt zich als een laagdoorlaatfilter.

Nu je convolutie begint te begrijpen zal ik de wiskundige vergelijking ervan geven. De asterisk (*) wordt normaal gebruikt om convolutie aan te geven:

$(f * g)(t) = \int f(\tau) g(t - \tau) d\tau$

In de bovenstaande vergelijking is $g(t)$ een van de twee signalen, het wordt omgedraaid en over $f(t)$ heen geschoven. Je kunt $g(t)$ en $f(t)$ omwisselen zonder gevolgen, het blijft dezelfde vergelijking. Meestal wordt het kortere signaal gebruikt als zijnde $g(t)$ . Convolutie staat gelijk aan de kruiscorrelatie, $\int f(\tau) g(t+\tau)$ , in het geval dat $g(t)$ symmetrisch is, dus wanneer het omdraaien geen effect heeft.

8.4. Filterimplementatie¶

We zullen niet te diep in de stof van filterimplementatie duiken. Ik leg liever de nadruk op filterontwerp (je kunt toch bruikbare implementaties vinden voor elke taal). Voor nu draait het om een ding: Om een signaal met een FIR-filter te filteren voer je convolutie uit tussen de impulsrespons (de coëfficiënten) en het ingangssignaal. In de discrete wereld gebruiken we digitale convolutie (voorbeeld hieronder).

De driehoeken met een $b_x$ ernaast zijn de coëfficiënten en de driehoeken met $z^{-1}$ geven een vertraging van 1 tijdstap aan.

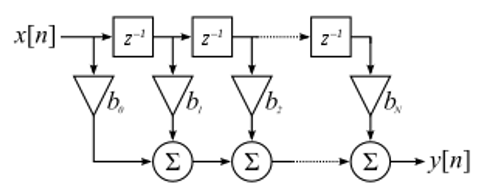
Implementation of a finite impulse response (FIR) filter with delays and taps and summations

Je ziet nu misschien wel waarom de coëfficiënten in het Engels “taps” worden genoemd, dit komt voort uit hoe het filter wordt geïmplementeerd.

FIR tegenover IIR¶

Er zijn grofweg twee verschillende typen filters: FIR en IIR

Finite impulse response (FIR)
Infinite impulse response (IIR)

We zullen niet diep op de theorie ingaan, maar onthoud voor nu dat FIR filters gemakkelijker te ontwerpen zijn en alles kunnen doen als er maar genoeg coëfficiënten worden gegeven. IIR-filters zijn efficiënter en zouden hetzelfde kunnen bereiken met minder coëfficiënten maar ook met het risico dat het filter instabiel wordt en niet goed werkt. Als een lijst coëfficiënten wordt gegeven, dan is dit over het algemeen voor een FIR-filter. Als er wordt gesproken over “polen” dan betreft het een IIR-filter. In dit boek zullen we het bij FIR-filters houden.

Het onderstaande figuur laat het verschil zien tussen een FIR en IIR-filter. Ze hebben hetzelfde gedrag maar het FIR-filter gebruikt 50 coëfficiënten en het IIR filter maar 12. Toch hebben ze beiden ongeveer dezelfde transitiebreedte.

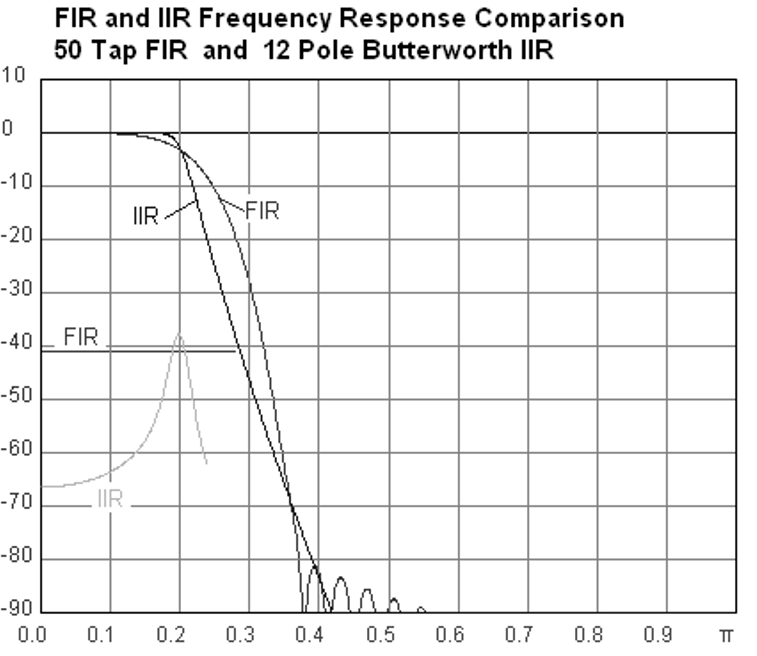
Comparing finite impulse response (FIR) and infinite impulse response (IIR) filters by observing frequency response

Wat je hieruit kunt leren is dat het FIR-filter veel meer computerkracht vereist dan een IIR-filter voor hetzelfde gedrag.

Hieronder staan wat voorbeelden van FIR en IIR-filters die je misschien in het echt al hebt gebruikt.

Wanneer je een “moving average” (voortschrijdend gemiddelde) filter over een lijst getallen toepast, dan is dat gewoon een FIR-filter met coëfficiënten van 1.

Vragen: Het is ook een laagdoorlaatfilter; waarom? Wat is het verschil tussen coëfficiënten van alleen 1’en of coëfficiënten die richting 0 vervallen?

Antwoorden

Een “moving average” filter is een laagdoorlaatfilter omdat het snelle veranderingen uitsmeert, de reden waarom mensen het willen gebruiken. Een reden om coëfficiënten te gebruiken die aan beide kanten richting 0 gaan is om plotselinge verandering aan de uitgang te voorkomen, zoals zou gebeuren als de ingang een tijd nul is en dan plotseling omhoog springt.

Voor een IIR-voorbeeld. Als je zoiets hebt gedaan:

x = x*0.99 + nieuwe_waarde*0.01

Waar de 0.99 en 0.01 de snelheid aangeven waarmee de waarde verandert. Dit is een handige manier om een variabele te veranderen zonder de vorige waarden te onthouden. Dit is een laagdoorlaat IIR-filter. Hopelijk kun je zien waarom dit minder stabiel is. De waarden zullen nooit volledig verdwijnen!

8.5. Filterontwerp¶

In de praktijk gebruiken de meeste mensen een ontwerptool of een softwarefunctie (bijv. Python/SciPy) om het filter te ontwerpen. We zullen eerst laten zien wat mogelijk is binnen Python voordat we naar externe tools gaan kijken. Onze focus ligt op FIR filters, omdat deze het meest worden toegepast voor digitale signaalbewerking.

Binnen Python¶

Als onderdeel van het ontwerpen van een filter, dus de coëfficiënten genereren voor onze gewenste respons, moeten we het type filter kiezen (laagdoorlaat, hoogdoorlaat, banddoorlaat of bandstop), de kantelfrequentie/frequenties, het aantal coëfficiënten en optioneel de transitiebreedte.

Er zijn twee manieren in SciPy die we zullen gebruiken om FIR-filters te ontwerpen, beide gebruiken de zogenaamde “raam-methode”. Als eerste is er scipy.signal.firwin() wat het meest rechttoe rechtaan is; het geeft de coëfficiënten voor een FIR-filter met een lineaire fase. De functie heeft het aantal coëfficiënten en kantelfrequentie nodig (voor laagdoorlaat/hoogdoorlaat) en twee kantelfrequenties voor banddoorlaat/bandstop. Optioneel kun je de transitiebreedte geven. Als je de samplefrequentie via fs doorgeeft, dan zijn de eenheden van je kantelfrequentie en transitiebreedte in Hz, maar als je het niet meegeeft dan zijn de frequenties genormaliseerd (0 tot 1 Hz). Het pass_zero argument is standaard True, maar als je een hoogdoorlaat- of banddoorlaatfilter wilt, dan moet je het op False zetten; het geeft aan of 0 Hz in de doorlaatband moet zitten. Het wordt aangeraden om een oneven aantal coëfficiënten te gebruiken, en 101 coëfficiënten is een goed startpunt. Laten we bijvoorbeleld een banddoorlaatfilter maken van 100 kHz tot 200 kHz met een samplefrequentie van 1 MHz:

from scipy.signal import firwin
sample_rate = 1e6
h = firwin(101, [100e3, 200e3], pass_zero=False, fs=sample_rate)
print(h)

De andere optie is om scipy.signal.firwin2() te gebruiken, wat flexibeler is en gebruikt kan worden om filters met een aangepaste frequentierespons te ontwerpen, omdat je een lijst van frequenties en de gewenste versterking bij elke frequentie geeft. Het vereist ook het aantal coëfficiënten en ondersteunt dezelfde fs parameter als hierboven genoemd. Laten we als voorbeeld een filter maken met een laagdoorlaatgebied tot 100 kHz, en een apart banddoorlaatgebied van 200 kHz tot 300 kHz, maar met de helft van de versterking van het laagdoorlaatgebied, en we zullen een transitiebreedte van 10 kHz gebruiken:

from scipy.signal import firwin2
sample_rate = 1e6
freqs = [0, 100e3, 110e3, 190e3, 200e3, 300e3, 310e3, 500e3]
gains = [1, 1,     0,     0,     0.5,   0.5,   0,     0]
h2 = firwin2(101, freqs, gains, fs=sample_rate)
print(h2)

Om het FIR filter ook echt op een signaal toe te kunnen passen zijn er verschillende opties, en ze vereisen allemaal een convolutie-operatie tussen de samples die we willen filteren en de coëfficiënten die we hierboven hebben gegenereerd:

np.convolve
scipy.signal.convolve
scipy.signal.fftconvolve
scipy.signal.lfilter

De bovenstaande convolutiefuncties hebben allemaal een mode argument die de opties 'full', 'valid', of 'same' accepteert. Het verschil zit in de grootte van de uitvoer, omdat bij het uitvoeren van een convolutie, zoals we eerder in dit hoofdstuk hebben gezien, er aan het begin en einde overgangsverschijnselen kunnen ontstaan. De 'valid' optie bevat geen overgangsverschijnselen, maar de uitvoer zal iets kleiner zijn dan het signaal dat aan de functie is gegeven. De 'same' optie geeft een uitvoer die even groot is als het ingangssignaal, wat handig is bij het bijhouden van tijd of andere tijd-domein signaal eigenschappen. De 'full' optie bevat alle overgangsverschijnselen; het geeft de volledige convolutieresultaat.

Nu gaan we alle vier convolutiefuncties op een testsignaal van witte Gausische-ruis toepassen met de filtercoefficienten die we hierboven hebben gemaakt. Let op dat lfilter een extra argument heeft (de 2e) die altijd 1 is voor een FIR-filter.

import numpy as np
from scipy.signal import firwin2, convolve, fftconvolve, lfilter

# Maak een testsignaal met gauschische ruis
sample_rate = 1e6 # Hz
N = 1000 # samples to simulate
x = np.random.randn(N) + 1j * np.random.randn(N)

# We maken weer het fir filter zoals hierboven
freqs = [0, 100e3, 110e3, 190e3, 200e3, 300e3, 310e3, 500e3]
gains = [1, 1,     0,     0,     0.5,   0.5,   0,     0]
h2 = firwin2(101, freqs, gains, fs=sample_rate)

# Het filter toepassen met de verschillende convolutiemethoden
x_numpy = np.convolve(h2, x)
x_scipy = convolve(h2, x) # scipys convolve
x_fft_convolve = fftconvolve(h2, x)
x_lfilter = lfilter(h2, 1, x) # Tweede argument is altijd 1 voor een FIR-filter

# Bewijs dat ze allemaal hetzelfde resultaat geven
print(x_numpy[0:2])
print(x_scipy[0:2])
print(x_fft_convolve[0:2])
print(x_lfilter[0:2])

Bovenstaande code laat zien hoe je de vier methoden kunt gebruiken, maar misschien vraag je je af welke het beste is. De onderstaande grafieken laten alle vier methoden zien voor verschillende hoevelheid coefficienten. Het werd uitgevoerd op een Intel Core i9-10900K.

../_images/convolve_comparison_100000.svg

Zoals je kunt zien, schakelt scypi.signal.convolve automatisch over naar een FFT-gebaseerde methode bij een bepaalde invoergrootte. Hoe dan ook, fftconvolve is de duidelijke winnaar voor deze grootte van coëfficiënten en invoer, wat vrij typische groottes zijn in RF-toepassingen. Veel code binnen PySDR gebruikt np.convolve: simpelweg omdat het een import minder is en het prestatieverschil verwaarloosbaar is voor lage datarates of niet real-time toepassingen.

Als laatste laten we dezelfde uitvoer in het frequentiedomein zien, zodat we eindelijke kunnen controleren of de firwin2-functie ook echt een filter heeft gegeven wat aan onze eisen voldoet. We beginnen met de code die ons h2 gaf:

# Simuleer een signaal van Gausische ruis
N = 100000 # signaallengte
x = np.random.randn(N) + 1j * np.random.randn(N) # complex signaal

# PSD van het ingangssignaal
PSD_input = 10*np.log10(np.fft.fftshift(np.abs(np.fft.fft(x))**2)/len(x))

# Filter toepassen
x = fftconvolve(x, h2, 'same')

# PSD van de uitgang laten zien
PSD_output = 10*np.log10(np.fft.fftshift(np.abs(np.fft.fft(x))**2)/len(x))
f = np.linspace(-sample_rate/2/1e6, sample_rate/2/1e6, len(PSD_output))
plt.plot(f, PSD_input, alpha=0.8)
plt.plot(f, PSD_output, alpha=0.8)
plt.xlabel('Frequency [MHz]')
plt.ylabel('PSD [dB]')
plt.axis([sample_rate/-2/1e6, sample_rate/2/1e6, -40, 20])
plt.legend(['Input', 'Output'], loc=1)
plt.grid()
plt.savefig('../_images/fftconvolve.svg', bbox_inches='tight')
plt.show()

We zien dat het banddoorlaatgebied 3 dB lager ligt dan het laagdoorlaatgebied:

Buiten dit is er nog een obscure optie om een signaal te filteren genaamd scipy.signal.filtfilt, wat “zero-phase filtering” uitvoert, wat helpt om kenmerken in een gefilterd tijdsignaal precies te behouden waar ze voorkomen in het ongefilterde signaal. Dit wordt gedaan door de filtercoëfficiënten twee keer toe te passen, eerst in de voorwaartse richting en dan in de omgekeerde richting. Dus de frequentierespons zal een gekwadrateerde versie zijn van wat je normaal zou krijgen. Voor meer informatie zie https://www.mathworks.com/help/signal/ref/filtfilt.html of https://docs.scipy.org/doc/scipy/reference/generated/scipy.signal.filtfilt.html.

Stateful Filtering¶

Als je een filter real-time wilt toepassen op opvolgende blokken van samples, dan heb je een stateful filter nodig. Dit betekent dat je elke aanroep de initiële condities geeft die uit de vorige aanroep van het filter zijn gehaald. Dit verwijdert overgangsverschijnselen die optreden wanneer een signaal start en stopt (immers, de samples die je tijdens opvolgende blokken invoert zijn aaneengesloten, mits je toepassing het kan bijhouden). De toestand moet tussen aanroepen worden opgeslagen, en moet ook aan het begin van je code worden geïnitialiseerd voor de eerste filteraanroep. Gelukkig bevat SciPy lfilter_zi dat initiële condities voor lfilter genereert. Hieronder staat een voorbeeld van het verwerken van blokken aaneengesloten samples met stateful filtering:

b = taps
a = 1 # voor FIR, niet-1 voor IIR
zi = lfilter_zi(b, a) # bereken de initiële condities
while True:
    samples = sdr.read_samples(num_samples) # Vervang dit met de functie van jouw SDR
    samples_filtered, zi = lfilter(b, a, samples, zi=zi) # filter toepassen

Externe Tools¶

Je kunt ook externe tools gebruiken om een eigen filter te ontwerpen. Voor studenten raad ik aan om deze gemakkelijke web app te gebruiken: http://t-filter.engineerjs.com. Het is gemaakt door Peter Isza en laat je de impuls- en frequentierespons zien. Op het moment van schrijven is de tool standaard ingesteld op een laagdoorlaatfilter met een doorlaatband van 0 tot 400 Hz en een stopband van 500 Hz en hoger. De sample-frequentie staat ingesteld op 2 kHz, dus de maximaal “zichtbare” frequentie is 1 kHz.

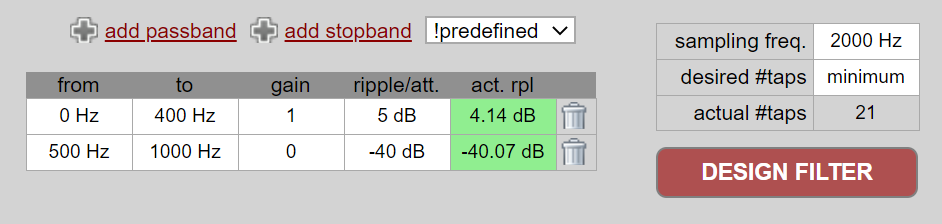
Klik op de “Design Filter” knop om de coëfficiënten te genereren en de frequentierespons te weergeven.

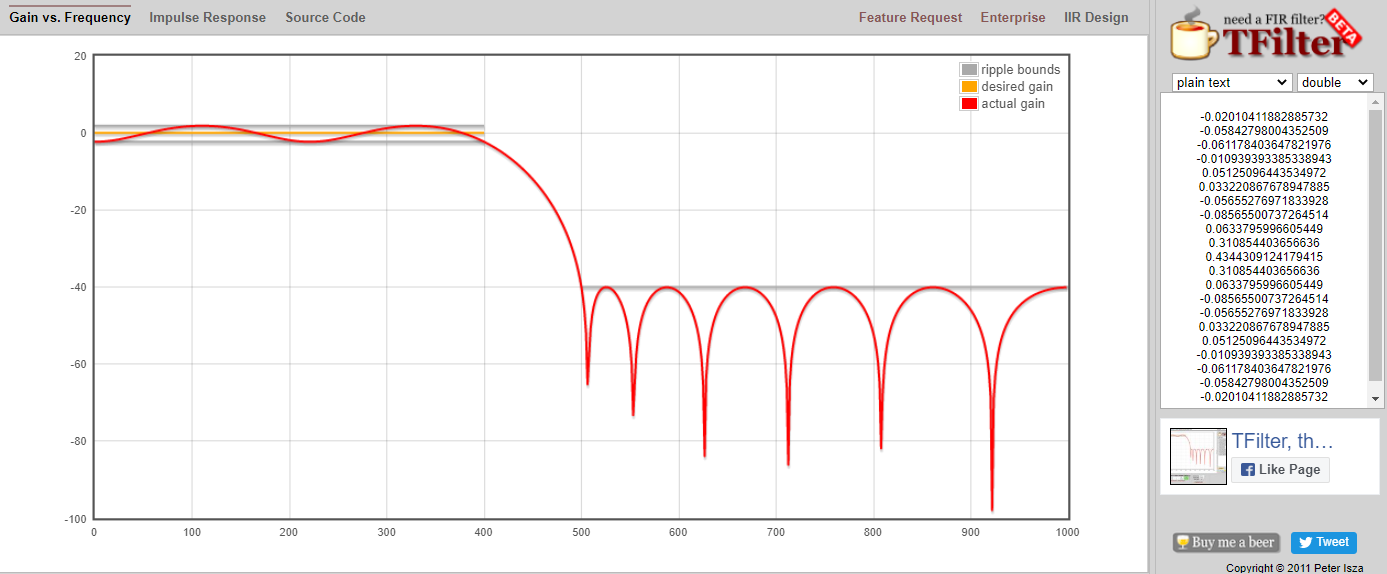
Klik op de “Impulse Response” link boven de grafiek om de impulsrespons te zien, wat een weergave is van de coëfficiënten omdat dit een FIR filter betreft.

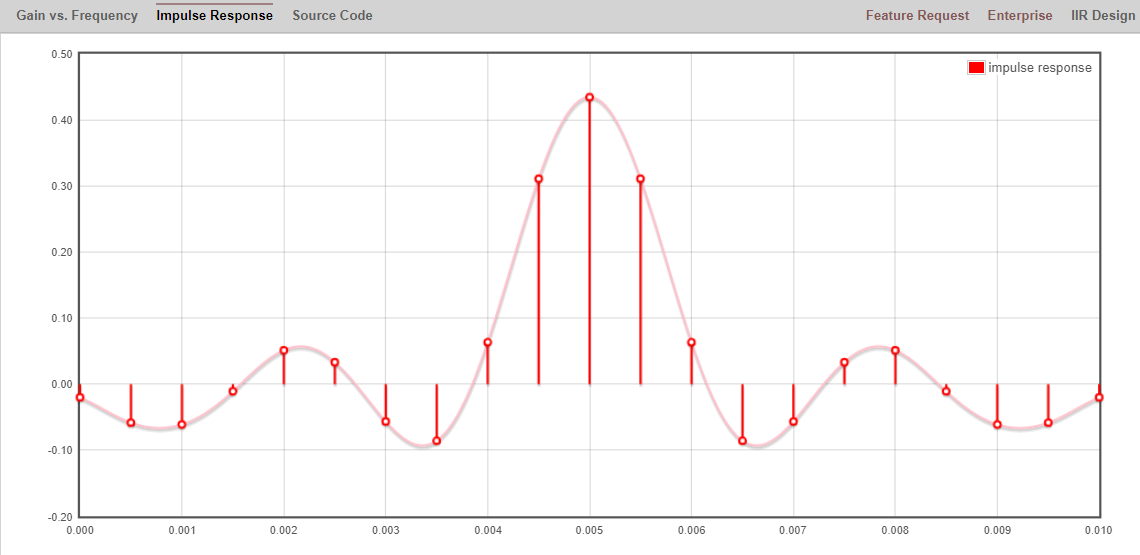
De app kan zelfs de C broncode genereren waarmee je dit filter kunt implementeren en gebruiken. De app heeft geen manier om een IIR-filter te implementeren omdat deze over het algemeen veel lastiger zijn om te ontwerpen.

8.6. Willekeurige frequentieresponsie¶

Nu gaan we een manier bekijken om in Python FIR-filters te ontwerpen op basis van onze gewenste frequentieresponsie. Er zijn vele manieren om een filter te ontwerpen, wij zullen in het frequentiedomein starten en terugwerken naar de impulsrespons. Uiteindelijk wordt het filter ook zo beschreven (in coëfficiënten).

Je begint met jouw gewenste frequentierespons in een vector plaatsen. Dus laten we een willekeurig laagdoorlaatfilter maken zoals hieronder:

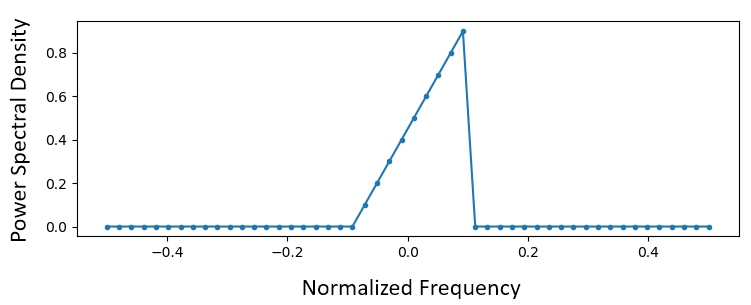
De code waarmee dit filter gemaakt wordt is vrij simpel:

import numpy as np
import matplotlib.pyplot as plt
H = np.hstack((np.zeros(20), np.arange(10)/10, np.zeros(20)))
w = np.linspace(-0.5, 0.5, 50)
plt.plot(w, H, '.-')
plt.show()

Je kunt arrays aan elkaar plakken met bijv. de hstack() functie. We weten dat dit zal leiden tot een filter met complexe coëfficiënten. Waarom?

Antwoord:

Het is niet symmetrisch rondom 0 Hz.

Ons doel is om de coëfficiënten van dit filter te vinden zodat we het kunnen implementeren. Hoe krijgen we de coëfficiënten uit deze frequentierespons? Nou, hoe zetten we het frequentiedomein terug naar het tijddomein? Met de geïnverteerde FFT (IFFT)! De IFFT-functie is vrijwel gelijk aan de FFT functie. We zullen eerst een IFFTshift moeten uitvoeren op ons gewenste frequentierespons voor de IFFT, en nog een IFFTshift na de IFFT (Nee, dit heft elkaar niet op, probeer maar). Dit lijkt een verwarrend proces, maar onthoud dat je altijd een FFTshift na een FFT en een IFFTshift na een IFFT moet uitvoeren.

h = np.fft.ifftshift(np.fft.ifft(np.fft.ifftshift(H)))
plt.plot(np.real(h))
plt.plot(np.imag(h))
plt.legend(['real','imag'], loc=1)
plt.show()

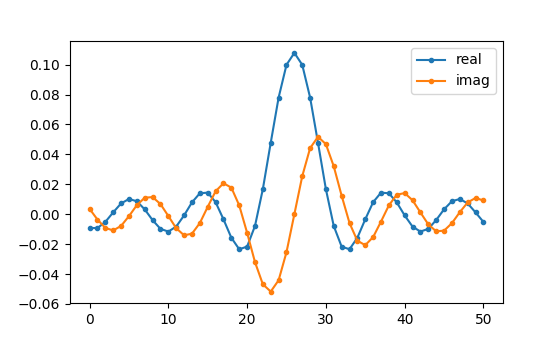
We gebruiken de bovenstaande coëfficiënten voor ons filter. We weten ook dat de impulsrespons en coëfficiënten hetzelfde zijn, dus wat we hierboven zien is onze impulsrespons. Laten we een FFT op onze coëfficiënten uitvoeren om te zien hoe het frequentiedomein eruit zou zien. We nemen een 1024-punten FFT om een hoge resolutie te krijgen:

H_fft = np.fft.fftshift(np.abs(np.fft.fft(h, 1024)))
plt.plot(H_fft)
plt.show()

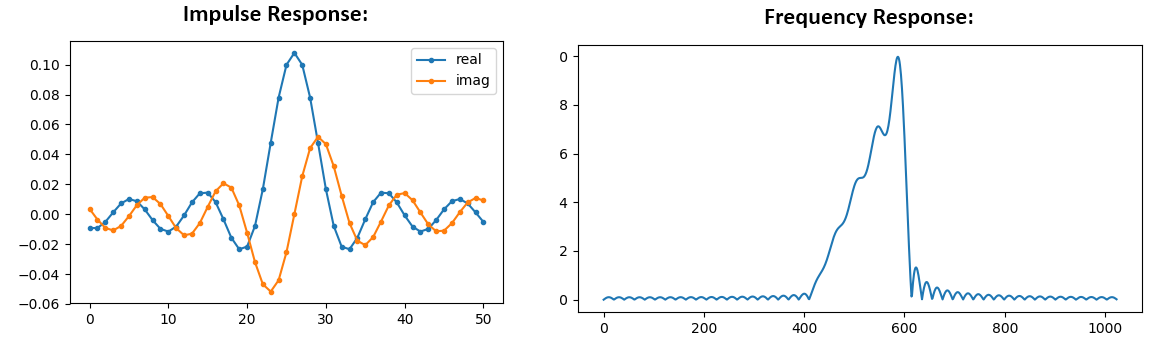
De frequentierespons is niet zo recht…. het komt niet echt overeen met het origineel, als je bedenkt wat voor vorm we hadden gemaakt. Een belangrijke reden hiervoor is omdat onze impulsrespons nog niet was uitgedoofd, dus de linker- en rechterkant gaan niet naar nul. Er zijn twee opties om dit wel voor elkaar te krijgen:

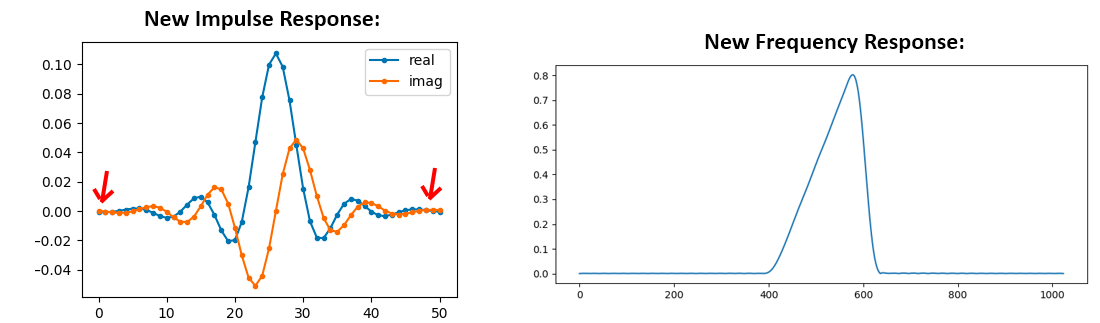
Optie 1: We passen een “venster” op de impulsrespons toe, zodat dat beide kanten naar 0 aflopen. Dit komt neer op een “vensterfunctie”, dat begint en eindigt bij 0, vermenigvuldigen met onze impulsrespons.

# Na h aangemaakt te hebben in het vorige stuk code
# het venster maken en toepassen
window = np.hamming(len(h))
h = h * window

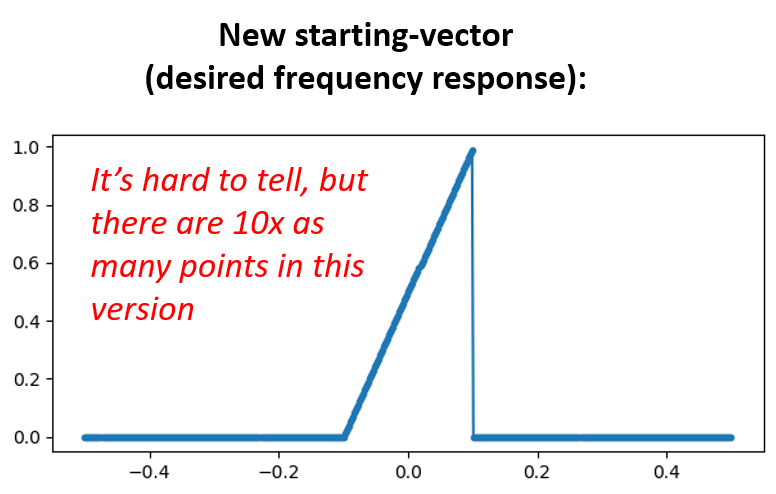
Optie 2: We maken een nieuwe impulsrespons die wel tijd heeft om naar 0 te gaan. We zullen de originele frequentierespons in resolutie moeten doen toenemen (dit heet interpoleren).

H = np.hstack((np.zeros(200), np.arange(100)/100, np.zeros(200)))
w = np.linspace(-0.5, 0.5, 500)
plt.plot(w, H, '.-')
plt.show()
# (de rest van de code blijft hetzelfde)

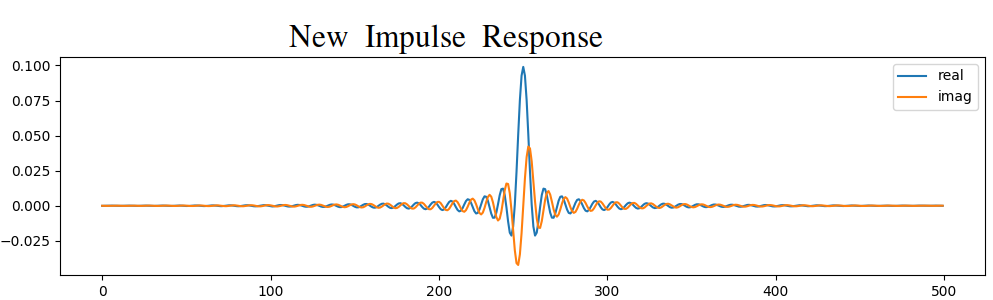
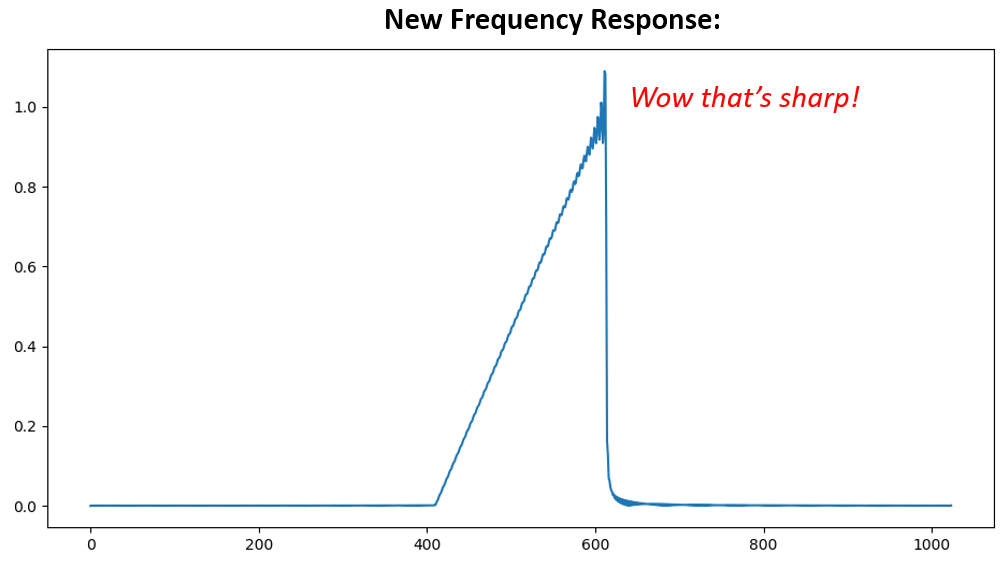
Beide versies werken. Welke zou jij kiezen? De tweede methode resulteerde in meer coëfficiënten, maar de eerste methode resulteerde in een frequentierespons die niet zo scherp of steil was. Er zijn vele manieren om een filter te ontwerpen, elk met zijn eigen afwegingen. Veel mensen beschouwen filterontwerp als een kunst.

8.7. Introductie tot Pulse Shaping¶

We zullen kort een interessant onderwerp binnen de DSP introduceren, pulse shaping, of pulsvorming in het Nederlands. In een later hoofdstuk zullen we dit onderwerp beter bestuderen, zie Pulse Shaping. Wat wel handig is om te benoemen, is dat pulsvorming uiteindelijk ook een type filter is voor een specifiek doel, met specifieke eigenschappen.

Zoals we hebben geleerd, gebruiken digitale signalen symbolen, om een of meerdere bits aan informatie aan te geven. We gebruiken modulatieschema’s zoals ASK, PSK, QAM, FSK, etc., om een draaggolf te moduleren zodat deze informatie draadloos verzonden kan worden. Toen we in het Digitale Modulatie hoofdstuk QPSK simuleerden, gebruikten we alleen 1 sample per symbool. In de praktijk gebruiken we meerdere samples per symbool en dat heeft te maken met filters.

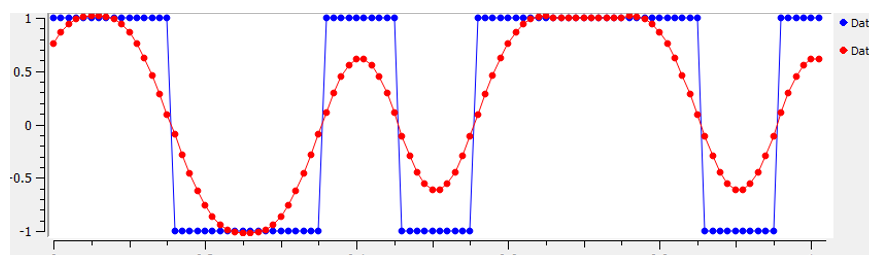
We gebruiken filters om onze symbolen te “vormen” in het tijddomein, want dit beïnvloedt de vorm in het frequentiedomein. Het frequentiedomein laat zien hoeveel spectrum ons signaal in beslag neemt, en dit is iets wat we gewoonlijk willen minimaliseren. Hierbij is het belangrijk om te beseffen dat de spectrale eigenschappen (frequentiedomein) van het signaal in de basisband niet zullen veranderen wanneer we een draaggolf ermee moduleren; het verschuift de basisband naar een hogere frequentie, maar de vorm, en bandbreedte, blijven hetzelfde. Wanneer we een enkele sample per symbool gebruiken is het alsof we een blokgolf versturen. In het geval van BPSK met 1 sample per symbool is het ook echt een blokgolf van 1’en en -1’en:

Maar zoals we eerder hebben geleerd, zijn blokgolven niet efficiënt want ze gebruiken een overbodige hoeveelheid van het spectrum:

Dus wat we doen is de blokkige symbolen “vormgeven” (dus pulse shaping) zodanig dat ze minder ruimte van het frequentiedomein innemen. We passen “pulse shaping” toe wanneer we een laagdoorlaatfilter gebruiken, want dit gooit de hogere frequentiecomponenten in onze symbolen weg. Hieronder is een voorbeeld te zien van een signaal met symbolen in de tijd (boven) en frequentie (onder), voor en na het vormgevende filter is toegepast.

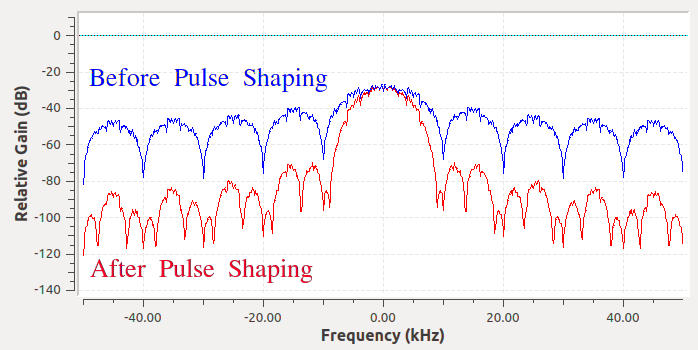
Demonstration of pulse shaping of an RF signal to reduce occupied bandwidth

Kijk eens hoeveel sneller het signaal in het frequentiedomein afzakt. De lobben aan de zijkant zijn ~30 dB zwakker na de pulsvorming; dat is 1000x minder! Nog belangrijker is dat de middelste lobbe smaller is, dus er wordt minder van het spectrum gebruikt voor dezelfde hoeveelheid bits per seconde.

De meest gebruikte filters om pulsvorming te realiseren zijn:

Raised-cosine filter
Root raised-cosine filter
Sinc filter
Gaussisch filter

Deze filters hebben over het algemeen een parameter die je in kunt stellen om de gebruikte bandbreedte te verminderen. Hieronder zie je een voorbeeld wat het tijd- en frequentiedomein laat zien van een raised-cosine filter met verschillende waarden voor $\beta$ , de parameter die bepaalt hoe steil het filter afloopt.

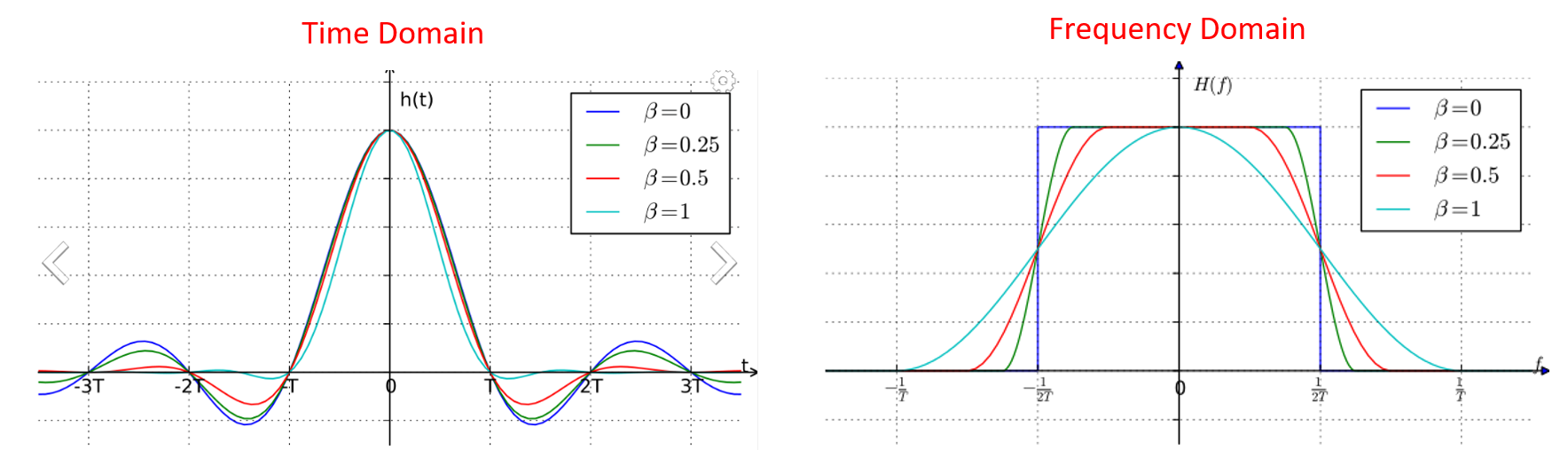
Hier is te zien dat een lagere waarde van $\beta$ het gebruikte spectrum vermindert (voor dezelfde hoeveelheid data). Maar, wanneer deze waarde te klein wordt dan zullen de tijddomein symbolen meer tijd nodig hebben om naar 0 te vervallen. En wanneer $\beta$ 0 is zullen de symbolen nooit naar 0 gaan wat inhoudt dat we dit in de praktijk niet kunnen versturen. Een waarde van 0.35 is normaal voor $\beta$ .

Je leert nog een hoop meer over pulsvorming, inclusief speciale eigenschappen waaraan de filters moeten voldoen, in het Pulse Shaping hoofdstuk.