9. 信道编码

在本章中，我们介绍信道编码（Channel Coding）的基础知识，包含前向纠错（Forwad Error Correction，FEC）、香农极限（Shannon Limit）、汉明码（Hamming Code）、涡轮码（Turbo Code）和低密度奇偶校验码（LDPC Code）等。 信道编码是无线通信中的一个巨大领域，是“信息论”的一个分支，信息论研究信息的量化、存储和传输。

为什么需要信道编码

正如我们在 噪声与分贝（dB） 章节中所学到的，无线信道是嘈杂的，我们的数字符号无法完美地到达接收器。如果你上过网络课程，你可能已经知道循环冗余校验（Cyclic Redundancy Checks，CRCs），它可以在接收端 检测 错误。 信道编码的目的是在接收端检测以及 纠正 错误。 带有差错允许的编码可以让我们在更高阶的调制方案下进行传输而不断链。 以下星座图是一个很好的可视化案例，显示在相同噪声下的 QPSK（左）和 16-QAM（右）调制。 QPSK 每个符号编码 2 bits 的信息，而 16-QAM 每个符号编码 4 bits（传输数据率是 QPSK 的两倍）。 如果我们把接收到的 QPSK 信号可视化在星座图中，当且仅当符号没有越过符号决策边界、或 x 轴 y 轴时，符号才能被正确解码。 对于 16-QAM 而言，其簇与簇之间间隙更小，更容易重叠，因此符号解码更容易出错。

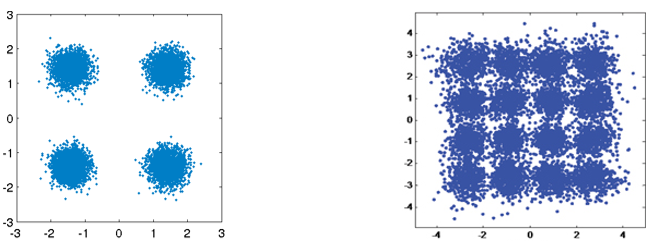
使用 CRC 时，我们只能检测错误，而不能纠正错误，因此出错后只能重传。 信道编码的目的是通过多传输一些精心设计的 冗余 信息，让接收端能够纠正错误。

在上文中，我们讨论了为何需要信道编码，接下来我们看看信道编码在发射-接收链路中的位置：

在发射-接收链路中有多步编码过程。 信源编码（Source Coding）是第一步，其目的是尽可能压缩要传输的数据，就像你压缩文件以减少占用空间一样。 换句话说，信源编码块的输出应该比数据输入 小，但信道编码的输出将比其输入大，因为添加了冗余信息。

信道编码的种类

为了进行信道编码，我们使用“纠错码（Error Correction Code）”。 最基本的编码称为“重复编码”，就是简单地将一个比特连续重复 N 次。对于重复-3 编码，每个比特将传输三次：

• 0 → 000
• 1 → 111

消息 “10010110” 在信道编码后传输为 “111000000111000111111000”。

某些编码在“块”输入位上工作，而其他编码则使用流式方法。 每次处理固定长度数据的编码称为“块编码”，而处理任意长度数据的编码称为 “卷积编码”。 这两种是主要的编码类型。我们的重复-3 编码是一个块编码，每个块为三位。

顺便提一下，纠错码的应用不仅仅限于无线通信中的信道编码。 你可能曾经把数据存储在机械硬盘或固态硬盘上，然后发现读取时从未出现过比特错误。 其实，从内存中写入数据再读出的过程，类似于一个通信系统。 硬盘和固态硬盘的控制器内部都集成了纠错功能，这个过程对操作系统来说是透明的，而且通常是专有的，因为所有功能都在硬盘或固态硬盘内部实现。 而对于像 CD 这样的便携式存储介质，纠错标准必须统一：例如，Reed-Solomon 码在 CD-ROM 中非常常见。

编码率

所有错误纠正都包含某种形式的冗余。这意味着如果我们想要传输 100 位信息，我们实际上需要发送超过 100 个比特。“编码率（Code-rate）”是信息位数与发送的总位数（即信息加冗余位）的比率。回到重复-3 编码的例子，如果我有 100 位信息，那么我们可以确定以下内容：

• 300 比特被发送
• 仅 100 比特表示信息
• Code-rate = 100/300 = 1/3

纠错码的编码率将始终小于 1。它代表了冗余程度和吞吐量的权衡，较低的编码率意味着更多的冗余和更少的吞吐量。

调制与编码

在 数字调制 章节中，我们讨论了不同噪音下的调制方式选择。 当信噪比较低时，需要使用低阶调制方案（比如 QPSK）来应对噪声；而当信噪比较高时，可以使用 256QAM 这样的高阶调制方案，以提高数据传输速率。 信道编码也是类似的情况：在低信噪比下，应选择较低的码率；而在高信噪比下，则可以使用接近 1 的码率。 现代通信系统采用了一套组合调制（Modulation）和编码（Coding）方案，称为 MCS（Modulation Coding Scheme）。 每种 MCS 都规定了在特定信噪比条件下应使用的调制和编码方式。

现代通信系统能够根据无线信道的实时状况，动态调整 MCS。 接收端会向发送端反馈信道的质量信息。 这些反馈必须在信道质量发生变化之前及时传递，通常在几毫秒内完成。 通过这种自适应机制，通信系统可以实现最高的数据传输效率，这一技术被广泛应用于 LTE、5G 和 WiFi 等现代通信技术中。 下面是一个蜂窝基站根据用户距离的变化，在传输过程中调整 MCS 的示意图。

使用自适应 MCS 时，如果你绘制吞吐量与 SNR 的关系图，你会得到一个阶梯形的曲线，如下图所示。 像 LTE 这样的协议通常有一个表格，指示在什么 SNR 下应该使用哪种调制和编码。

汉明码

让我们来学习一个简单但是精巧的纠错码 — 汉明码（Hamming Code）。 1940年代末，Richard Hamming 在贝尔实验室工作，使用一台依赖穿孔纸带的机电计算机。 当计算机检测到错误时，它会停止运行，需要操作员手动修复。 汉明对每次遇到错误都要从头开始重启程序感到非常沮丧。 他抱怨说：“真见鬼，既然机器能检测到错误，为什么不能自动定位并修正这些错误呢？” 于是，他在接下来的几年里开发了汉明码，使计算机能够自动检测并纠正错误。

在汉明码中，通过添加一些额外的位，即奇偶校验位或检查位，来增加数据的冗余性。 这些奇偶校验位位于所有 2 的幂次的位置上，比如 1, 2, 4, 8 等等。 其他位置则用于存储实际的数据。 下面的表格用绿色标出了奇偶校验位。 每个奇偶校验位都会“覆盖”那些与奇偶校验位位置进行按位与运算后结果非零的位，这些位在表格中用红色X标记。 如果我们想要使用某个数据位，就需要知道哪些奇偶校验位覆盖了它。 例如，要使用数据位 d9，就需要奇偶校验位 p8 以及所有在它之前的奇偶校验位。 这个表格可以帮助我们确定对于特定数量的数据位，需要多少个奇偶校验位。 这种模式可以无限扩展。

汉明码是一种块编码方式，它每次处理 N 个数据位。 通过使用三个校验位，我们可以每次处理四个数据位的块。 这种错误编码方法被称为 Hamming(7,4)，其中第一个数字表示传输的总位数，第二个数字表示实际的数据位数。

以下是汉明码的三个重要特点：

• 从一个码字转换到另一个码字至少需要改变三位
• 它能够纠正单个位的错误
• 它能检测但不能纠正两个位的错误

从算法的角度来看，编码过程可以通过简单的矩阵乘法来实现，使用的是一种称为“生成矩阵（Generator Matrix）”的工具。 在下面的例子中，向量 1011 是要编码的数据，也就是我们希望发送给接收者的信息。 二维矩阵就是生成矩阵，它定义了编码的方式。 通过矩阵乘法得到的结果就是我们要传输的码字。

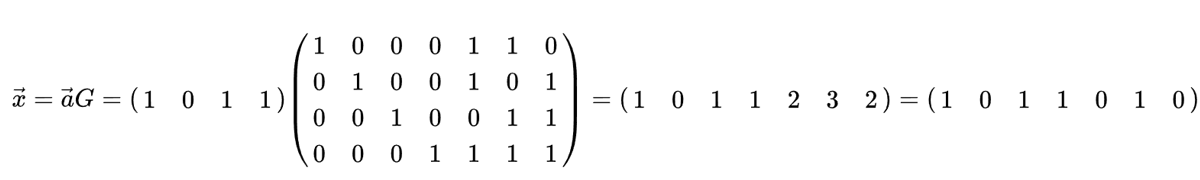
我们深入探讨汉明码的目的，是为了让大家对错误编码的工作原理有一个初步的了解。 块码通常遵循类似的模式。 虽然卷积码的工作方式有所不同，但这里不作详细讨论。 卷积码通常使用 Trellis 风格的解码方法，这种方法可以用一个类似下图的形式来表示：

软判决解码 vs 硬判决解码

回想一下，在接收端，信号先经过解调再进行解码。解调器可以告诉我们它认为发送的是哪个符号，也可以输出一个“软”值。 以 BPSK 为例，解调器不会简单地告诉我们 1 或 0，而是会给出 0.3423 或 -1.1234 这样的“软”值。 通常，解码方法会设计为使用硬值或软值。

• 软判决解码（Soft Decision Decoding） – 输出软值
• 硬判决解码（Hard Decision Decoding） – 只输出 1 和 0

软判决解码更加可靠，因为它利用了所有可用的信息，但实现起来也更为复杂。我们之前讨论的汉明码采用硬判决，而卷积码则通常使用软判决。

香农极限

香农极限（Shannon Limit）或香农容量（Shannon Capacity）是一个令人难以置信的理论，它告诉我们信道每秒可以发送多少比特无错误的信息：

• C – 信道容量 [比特/秒（bit/sec）]
• B – 信道带宽 [赫兹（Hz）]
• S – 平均接收信号功率 [瓦特（Watt）]
• N – 平均噪声功率 [瓦特（Watt）]

这个公式表示了在信噪比足够高以实现无误传输的情况下，任何调制编码方案（MCS）所能达到的最佳性能。 更直观的是以每赫兹每秒比特数（bit/sec/Hz）来表示这个极限：

这里 SNR 用线性单位表示（而不是 dB）。 但在绘图时，为了方便，我们通常用 dB 表示 SNR：

如果你在其他地方看到的香农极限图有所不同，可能是它们使用了“每比特能量”或 作为横坐标，这只是另一种表示 SNR 的方式。

当信噪比相当高（例如，10 dB 或更高）时，香农极限可以简化为 ，这大约等于 （解释在 这里 ）。 例如，在 24 dB 的信噪比下，每赫兹每秒可以传输 8 bits，所以如果你有 1 MHz 的带宽，那就是 8 Mbps。 你可能会想，“这只是理论上的极限”，但现代通信技术已经非常接近这个极限，因此至少它可以给你一个大致的概念。 你也可以把这个数字减半，以考虑数据包/帧开销和非理想的 MCS。

根据规范，802.11n WiFi 在 2.4 GHz 频段（使用 20 MHz 宽的信道）的最大吞吐量是 300 Mbps。 显然，你可以紧挨着路由器坐，获得极高的信噪比，比如 60 dB，但为了可靠性和实用性，最大吞吐量的调制编码方案（回想上面的阶梯曲线）不太可能需要如此高的信噪比。 你可以查看一下 802.11n 的 MCS 列表 。 802.11n 最高支持 64-QAM，结合信道编码，根据 这张表 ，它需要约 25 dB 的信噪比。 这意味着，即使在 60 分贝的信噪比下，你的 WiFi 仍然会使用 64-QAM 。 因此，在 25 dB 时，香农极限大约是 8.3 bit/sec/Hz，给定 20 MHz 的带宽，就是 166 Mbps。 然而，当你考虑到 MIMO 技术（我们将在未来的章节中讨论），你可以并行运行四个这样的数据流，从而达到 664 Mbps。 将这个数字减半，你得到的结果非常接近 802.11n WiFi 在 2.4 GHz 频段宣传的最大速度 300 Mbps。

香农极限背后的证明相当复杂，它涉及的数学公式看起来像这样：

更多信息可以参考 这里.

当前最先进的编码技术

目前，最佳的信道编码方案是：

1. Turbo 编码，广泛应用于 3G、4G 通信系统以及 NASA 的航天器。
2. LDPC 编码，用于数字视频广播（DVB-S2）、WiMAX 和 IEEE 802.11n 无线网络标准。

这两种编码技术都接近了理论上的香农极限（即，在特定的信噪比条件下几乎达到了这一极限）。 相比之下，汉明编码等较为简单的编码方式距离香农极限还有很大差距。 从研究角度来看，编码技术本身已经很难再有大的突破。 当前的研究重点更多放在如何提高解码的计算效率，以及如何更好地适应信道反馈上。

低密度奇偶校验（Low-Density Parity-Check，LDPC）编码是一种非常高效的线性分组编码技术。 这种编码方法最早由 Robert G. Gallager 在 1960 年的 MIT 博士论文中提出。 由于其实现的计算复杂度较高，直到 1990 年代才开始受到重视！ 撰写本文时（2020 年），加拉格尔先生已经 89 岁高龄，依然健在，并因其开创性的研究获得了多项荣誉（这些荣誉是在他完成这项工作数十年后获得的）。 LDPC 编码不受专利保护，因此可以免费使用（而 Turbo 编码则需要支付专利费），这也是它被广泛应用于多种开放协议的原因。

Turbo 编码则是基于卷积编码的一种技术。 它通过结合两个或多个简单的卷积编码和一个交织器来实现。 Turbo 编码的基本专利申请于 1991 年 4 月 23 日提交。 由于其发明者是法国人，因此当高通公司希望在 3G 的 CDMA 系统中使用 Turbo 编码时，不得不与法国电信达成付费专利许可协议。 该专利的主要部分已于 2013 年 8 月 29 日到期。