3. IQ 采样¶
在本章中,我们将介绍 IQ 采样(也称复数采样或正交采样)。 我们还将涉及奈奎斯特采样(Nyquist Sampling)、复数、射频载波(RF Carriers)、 下变频(Downconversion)、以及功率谱密度(Power Spectral Density)等概念。 IQ 采样是软件定义无线电(SDR)以及许多数字接收机(和发射机)执行的采样形式。 它是常规数字采样的稍微“复”杂一些的版本(这里有个双关语,哈哈),本章讲娓娓道来并教会你如何实践,相信你一定能理解透彻!
什么是采样¶
在深入讨论 IQ 采样之前,我们先来讨论什么是采样。其实,你在使用麦克风录音时已经遇到它了: 麦克风是一种传感器,它将声波转换成电信号(电压)。这个电信号被 ADC(模数转换器)转换成声波的数字表示。 简化来说,麦克风捕捉声波,将声转换成电,然后将电转换成数字。可以看出,ADC 是模拟领域和数字领域之间的桥梁。 SDR 与麦克风惊人地相似,只不过使用天线而不是麦克风接收信号,它的内部也使用了 ADC。 在两种情况中,电压水平都是由 ADC 进行采样的。你可以把 SDR 设备想象成以无线电波而不是声波为输入的麦克风。
无论是处理声波还是无线电波,如果我们想要数字化捕捉、处理或保存一个信号,就必须对其进行采样。 采样这个过程看似简单,实际上还挺复杂。 采样一个信号的技术性描述是:在一系列特定时刻捕捉信号的值,并将其数字化保存。 举个例子,假设对一个随机的连续函数 \(S(t)\) (它可以代表任何事物)进行采样:
我们会以固定间隔时间 \(T\) 秒记录 \(S(t)\) 的值,这个间隔被称为 采样周期 。 我们采样的频率,即每秒采集的采样点数量 \(\frac{1}{T}\) 称为 采样率 ,它是采样周期的倒数。 例如,采样率为 10 Hz 相当于采样周期为 0.1 秒,每个采样点之间将会有 0.1 秒的间隔。 在实际应用中,采样率通常为数百 kHz 、数十 MHz 乃至更高。当我们对信号进行采样时,需要首先注意采样率,这是一个非常重要的参数。
有些人可能更喜欢看到公式定义:让 \(S_n\) 代表采样点 \(n\) , 采样过程可以用数学形式表示为 \(S_n = S(nT)\) , \(n\) 是从 0 开始的整数。 即,我们在间隔 \(nT\) 的一系列时间点上评估模拟信号 \(S(t)\) 。
奈奎斯特采样¶
在处理一个特定信号时,我们常常会有个疑问:采样率多高合适? 考虑一个简单的正弦波信号,其频率为 f ,如下的绿色波形所示。 假设我们以 \(Fs\) 的频率采样(采样点以蓝色表示)。 如果我们的采样率等于信号频率(即 \(Fs = f\) ),那么看起来会像是下图这样:
上图中的红色虚线代表了一种与原函数不同(且错误的)映射。 这说明我们的采样率过低,在采样过程中产生了歧义,因为同一组采样点数据可能源自两个完全不同的函数。 若要准确重建出原始信号,我们必须避免这种采样歧义。
让我们调高一点采样率试试,比如 :math:` Fs = 1.2f` :
可以看到老问题仍然存在:采样点拟合出来的函数还是错的。这种信号重建歧义表明,如果某人提供给我们这些采样点数据就是这些,我们并不能重建出真实的原始信号。
再高一点试试,比如 Fs = 1.5f:
还是不够高!事实上,根据一条(我们不打算深入讨论的) DSP 理论:我们必须以信号频率的至少 两倍 采样才能消除歧义。
这次重建的信号没有误差是因为我们的采样速率足够快,以致于除了你所看到的信号之外,不存在其他任何其他也能与这些采样点吻合的信号 (当然,如果考虑更 高 频率的情况则另当别论,这一点我们稍后再详细讨论)。
在之前的例子中,我们使用的是一个简单正弦波信号,但现实世界的信号大都包含多个不同的频率分量。 为了准确地采样任何特定信号,采样率必须达到“最高频率分量频率的至少两倍”。 以下是一个频谱图示例,请注意,由于信号总会伴随一定的底噪,因此最高频率分量往往只能靠估计。
我们必须确定最高频率成分,然后确保我们的采样率不低于这个数值的两倍。 这个恰好两倍的频率被称为奈奎斯特频率。换句话说,奈奎斯特频率是一个(有限带宽)信号可被正确重构的采样最低速率, 它是 DSP 和 SDR 中一个极其重要的理论基础,是架在连续信号和离散信号之间的桥梁。
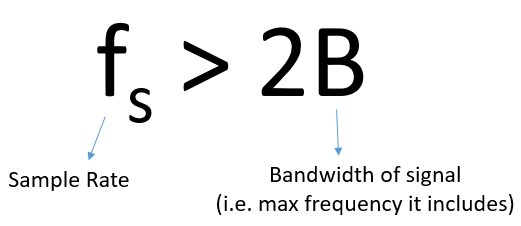
如果采样速度不够快速,会出现一个称为混叠(Aliasing)的现象,我们后面会详细讲解,现在仅需知道我们必须不惜一切代价避免它。 SDR 设备以及大多数接收机都会在执行采样之前过直接滤掉所有超过 \(Fs/2\) 的频率成分。 所以如果采样率设置的太低,前置的滤波器甚至直接就把我们想要收集的信号给截断了。 毕竟,所有的 SDR 设备都会努力地确保提供给我们的采样点不受混叠和其它因素的影响!
正交采样¶
“正交”这个术语有多重含义,但在 DSP 和 SDR 领域指的是两个相位偏移 90 度的波形。 为何相位偏移 90 度就正交了呢?可以这样想,当两个波形的相位差为 180 度时,它们实际上是同一波形,只不过一个波形的幅度被取了负值。 当它们的相位差为 90 度时,这两个波形就变成了互相正交的。更重要的是,相互正交的函数有很多独特应用。 为了便于理解和使用,我们通常以一个正弦波和一个余弦波来代表两个相位差为 90 度(正交)的正弦波。
我们还需要定义变量去代表正弦函数和余弦函数的 幅度 (amplitude)。 我们将以 I 来代表余弦函数 \(cos()\) 的幅度,用 Q 来代表正弦函数 \(sin()\) 的幅度:
将 I 和 Q 设为 1,我们将看到:
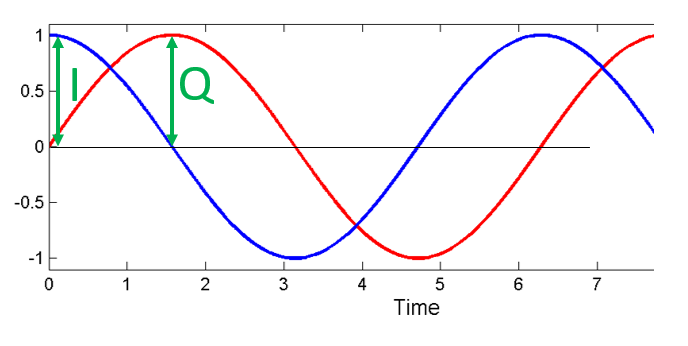
我们将 \(cos()\) 函数称作“同相”分量,简称为 I (In-Phase)分量, 而将 \(sin()\) 函数称作偏移 90 度相位的“正交”分量,简称为 Q (Quadrature)分量。 不过就算你不慎把 \(cos()\) 当作了 Q,把 \(sin()\) 当作了 I,大部分情况下也不会导致结果错误。
正交采样(又称为 IQ 采样)从发射机的角度更好理解。假如我们要发射一个信号,它的频率是 \(f\) ,幅度是 \(A\) ,相位是 \(\phi\) :
哦,对了,这里相位前面的负号只是约定俗成。 真实的信号往往在不同时刻具有不同的幅度和相位,因此,我们可以把幅度、相位都定义为关于时间的函数,如下面公式所示。
在射频电路中,控制正弦波的幅度很简单,但控制相位却很困难,因此我们可以利用三角恒等式: \(a \cos(x) + b \sin(x) = A \cos(x - \phi)\) , 它告诉我们可以通过两路特定幅度、初始相位为0、同频率的正弦信号和余弦信号来合成一个具有特定初始相位和幅度的余弦信号。 在无线领域,我们习惯用 I 来代替上式中的 \(a\) ,用 Q 来代替上式中的 \(b\) ,同时带入 \(x = 2 \pi f t\) ,我们就得到了:
其中:
这个数学机制意味着,通过控制 I 和 Q 两个分量,我们就可以合成出任意幅度和相位的余弦波。 下面的电路就落实了这个思路:
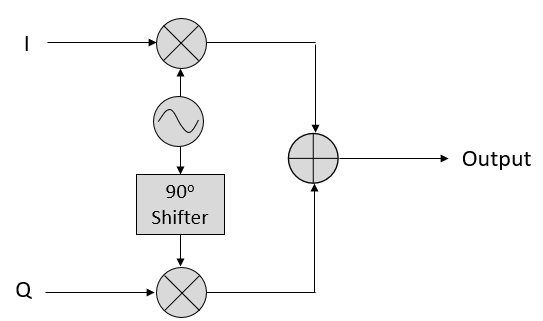
这意味着,假设我们有一个 IQ 采样点(它是一个复数,即 \(I + jQ\) ),我们可以将它调制到一个余弦波上,其幅度和相位由这个复数所定义:
了解数学原理后,我们通过可视化来直观感受一下如何将两个相位差 90 度的正弦波相加。 在下面的视频中,有一个滑块用于调整 I ,还有一个滑块用于调整 Q ,即余弦和正弦的幅度。 绘制的是余弦(红色)、正弦(蓝色)以及两者的和(绿色)。
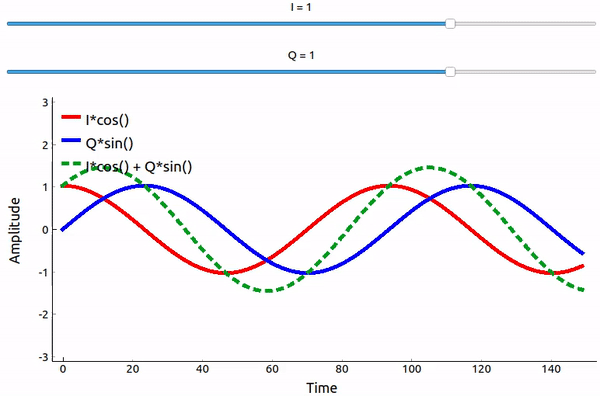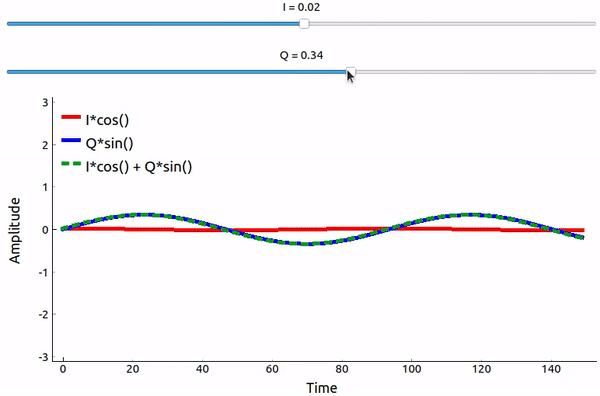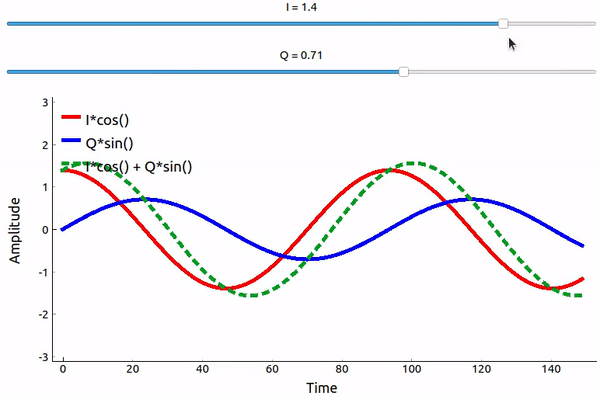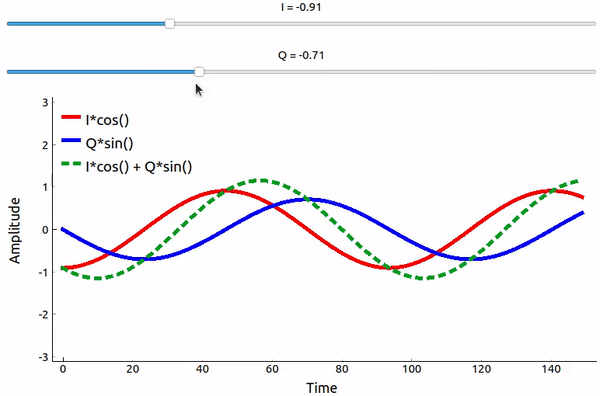
(上图是基于 pyqt 制作的,源代码可见 这里 )
从上文可以得到一个重要的结论,当我们将 \(cos()\) 和 \(sin()\) 相加时,我们得到的是另一个具有不同相位和幅度的余弦波。 此外,随着我们慢慢去除或添加其中的一个分量,它们的和的相位、幅度会发生变化。 这种构造的“实用性”在于,我们可以通过调整 I 和 Q 的幅度来控制所得到的正弦波的相位和幅度(同时不需要调整余弦或正弦的相位)。 例如,通过调整 I 和 Q 的值,我们可以输出幅度不变,但是具有任意相位的正弦波。 对于信号发射机而言,这种构造方法非常有用,因为调整两个固定相位正余弦波的幅度并进行加法操作比同时调整一个正弦波的幅度和相位要容易得多。 这也使我们能够更方便地表示基带信号,使其与载波无关。
复数¶
IQ 是一种表示信号幅度和相位的方式,它最终会将我们引向复数和复平面。 你可能在其他课程中已经见过复数。以复数 0.7-0.4j 为例:
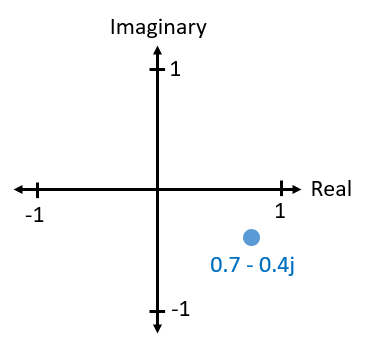
它实际上是由两个部分组成的,一个是实部,一个是虚部。 在将复数视为向量而不是点时,复数还将具有幅度和相位的概念。 幅度表示了从原点到该点的线段的长度(即向量的模长),而相位则表示了该向量与 0 度方向的夹角,而 0 度方向被定义为正实轴。
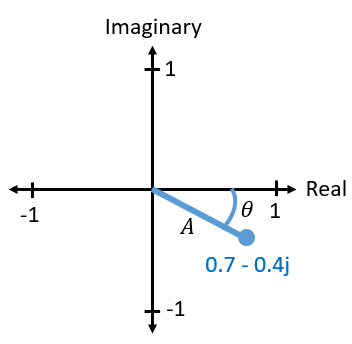
这种正弦波的复平面表示被称为“相量图”(phasor diagram)。 它将把复数绘制为向量。 现在我们来计算一下我们上文例子中复数 0.7-0.4j 的幅度和相位。 给定的复数如下,其中 \(a\) 是实部,\(b\) 是虚部:
在 Python 中,你可以使用 np.abs(x) 和 np.angle(x) 来计算复数的幅度(模长)和相位。
输入可以是一个复数或一个复数数组,输出将是一个或多个 实 数(数据类型为浮点数)。
在这个向量或相量图中,I 代表实部,Q 代表虚部,这就是大家习惯的 IQ 表示法。 之后,在画复平面时,我们将用 I 和 Q 标注实部和虚部。注意,以此就将 IQ 分量构造的信号波形以复数的方式表达了!
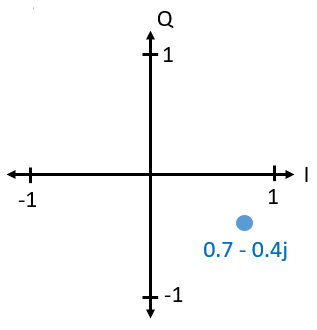
现在,假设我们要传输一个点:0.7-0.4j,这对应到 IQ 信号构造上意味着我们将传输:
我们可以使用三角恒等式 \(a \cos(x) + b \sin(x) = A \cos(x-\phi)\) 来进一步转换。 其中 \(A\) 表示我们使用 \(\sqrt{I^2 + Q^2}\) 计算出的幅度, \(\phi\) 表示相位,它等于 \(\tan^{-1} \left( Q/I \right)\) 。 现在上面的公式将恒等变换为:
虽然看起来我们在对一堆复数进行各种操作,但实际上这意味着我们在传输具有特定幅度和相位的信号。 现实世界中当然无法用电磁波传输虚数。我们只是借用了虚数/复数的数学定义来表示我们所传输的内容。 关于上面公式里的 \(f\) ,我们稍后会详细讨论。
FFT 中的复数¶
上文出现的所有复数都代表着信号的时域采样,但在计算 FFT 时我们还会再遇到复数,虽然在上一章讨论傅里叶级数和 FFT 时还没有来得及深入讨论。 当对一系列采样进行 FFT 后将得到它们的频域表示。 我们已经知道了 FFT 如何计算出这组采样中存在哪些频域分量(FFT 的幅度表示每个频率的强度)。 但是,FFT 其实还能找出每个频域分量对应的正弦波形在时间上的偏移(符合这些偏移的一组正弦波叠加才能重构时域信号)。 这个延迟即为 FFT 的相位。 FFT的输出是一个复数数组,每个复数对应一个频域分量,自然包含了上述的幅度和相位信息,该数组的索引则表示这个分量的频率(frequency bin)。 如果按照这些频率/幅度/相位生成正弦波并将它们叠加,就能得到原始的时域信号 (或者是非常接近原始信号的结果,由奈奎斯特采样定理所约束)。
接收机¶
现在让我们从无线电接收的角度来看(例如 FM 电台)。 IQ 采样的电路如下:
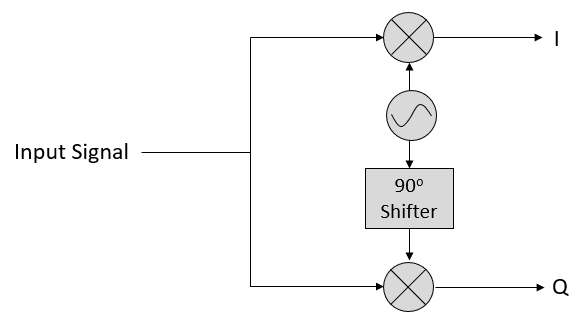
天线接收到实信号,然后将其分解为 IQ 值。 硬件上其实是通过两个 ADC 分别对 I、 Q 分量进行采样,然后将它们以复数的格式存储。 换句话说,每隔一个采样时间,设备将采样一个 I 值和一个 Q 值,并以 \(I + jQ\) 的形式组合起来(即每个 IQ 采样点对应到一个复数)存储。 这个采样的频率也就是我们常说的“采样率”。 比如,“我有一个采样率为 2 MHz 的 SDR 设备” 的意思是这个 SDR 设备每秒接收并存储两百万个 IQ 采样点(两百万个复数)。
如果有人给你一堆 IQ 采样点,它们看起来会像一个一维的复数数组/向量。无论是复数还是非复数,这一点是整个章节中的重点,我们终于讲到这里了!
读完整本书,你会对 IQ 采样的工作原理变得 非常 熟悉, 比如:如何通过 SDR 接收和传输它们、如何在 Python 中对它们进行处理、如何将它们保存到文件以供后续分析。
最后,请记住:上文图表展示的是 SDR 的内部机制。 在现实工作中,我们并不需要手动生成正弦波、平移90度、执行乘法或加法。 因为 SDR 将替我们完成这些内在操作,我们只需要告诉 SDR 以什么频率接收或传输我们的采样点。 在开发接收机时,SDR 将会提供给我们 IQ 数据(采样点)。 在开发发射机时,我们将 IQ 数据输入 SDR,数据类型是复数整数/复数浮点数。
载波和下变频¶
到目前为止,我们还没有讨论过频率,但我们在涉及 \(cos()\) 和 \(sin()\) 的方程中能看到它的身影:\(f\) 。 这个频率是我们发送的信号的中心频率(即电磁波的频率)。 我们将其称为“载波”,因为它在特定的射频频率上“运载”我们的信号。 当我们用 SDR 调谐到一个频率并接收采样点时,我们的信号仅仅存储在 I 和 Q 中(而与 \(f\) 无关)! 即假设我们调谐到了这个载波,那么这个载波不会在 I 和 Q 中显示出来。
作为参考,无线电信号(例如 FM 收音机、Wi-Fi、蓝牙、LTE、GPS 等)通常使用 100 MHz 到 6 GHz 之间的频率的载波。 这些频率下的载波在空气中传输效果非常好,不需要特别长的天线或大量功率来进行传输或接收。 微波炉使用 2.4 GHz 的电磁波来加热食物。如果微波炉的门没关好,泄露的电磁波会对 Wi-Fi 信号产生干扰,甚至可能灼伤皮肤。 另一种电磁波是光,可见光的频率大约为 500 THz。它是如此的高,以至于我们没法使用传统的天线,而是使用半导体器件(如 LED)来传输。 当电子在半导体材料的原子轨道之间跃迁时,它们会激发出光,其颜色(频率)可由跃迁的距离决定。 技术定义上,所谓无线电的频率为大约 20 kHz 到 300 GHz,因为是振荡电流能够从导体(天线)上辐射出来并通过空间传播的范围。 其中,100 MHz 到 6 GHz 是较为常用的频率范围(至少对于大多数现代应用来说是如此)。 6 GHz 以上的频率几十年来一直被用于雷达和卫星通信, 近年来则开始在 5G 的 “mmWave(毫米波)” (24 - 29 GHz)波段中被用于补充低频段以增加速度。
当我们快速改变载波的 IQ 值并传输时,这就是在对载波进行“调制”,调制的节奏和方法就是我们想要传输的数据。 改变 IQ 值等价于改变这一瞬间载波的相位和幅度。当然,也可以选择直接改变载波的频率,这就是常见的调频(FM)广播所采用的方法。
我们在上文谈到了两种无线电波,分别是我们想要传输的(通常包含许多频率分量)信号和单一频率的载波,你可能对此感到很困惑。 因此接下来我们将讨论基带信号与带通信号之间的区别,希望能厘清这一点。
现在让我们暂且回到采样的问题。 与其将信号直接乘以 \(cos()\) 和 \(sin()\) 然后记录 IQ 值来接收采样点, 将信号从天线先传入一个单一的 ADC(就像我们先前讨论的直接采样架构中那样)会不会更好? 毕竟,假设载波频率是 2.4 GHz(比如 Wi-Fi 或蓝牙)的,那么根据奈奎斯特采样定理,我们必须以至少 4.8 GHz 的速度采样。 这个采样率高得吓人,能满足这一要求的 ADC 将价值数千美元! 因此,相较于直接采样,我们会先将信号“下变频”,使得我们要采样的信号以 DC 或 0 Hz 为中心。 这种降频发生在采样之前,我们将从:
转为收集单纯的 I、Q 值。
让我们在频域可视化这一下变频的过程:

现在,中心频率变成了 0 Hz,最大频率不再是 2.4 GHz,而是源于(基带)信号自身的特性,因为我们已经去除了载波。 而大多数信号的带宽介于 100 kHz 和 40 MHz,因此通过下变频,我们可以以 更 低的速率进行采样。 B2x0 USRP 和 PlutoSDR 都包含一个射频集成电路(RFIC),采样率最高可达 56 MHz,这对于我们遇到的大多数信号来说都足够了。
需要强调一下,下变频的过程由我们的 SDR 设备自动执行。 作为用户,我们只需要告诉它要调谐到哪个频率即可。 下变频(和上变频)由一个称为混频器的组件完成,它在图表中通常画成一个包含乘法符号的圆圈。 混频器接收一个信号,输出下变频/上变频后的信号,此外还有个第三端口用于输入振荡器(LO)的信号。 振荡器将使得源信号的频率发生与振荡器频率相等的移位,所以混频器本质上只是一个乘法函数(记住,将信号乘以正弦波便可以使之频率发生移位)。
最后,你可能好奇信号在空气中传播的速度有多快。 从高中物理课上,我们学过无线电波只是低频电磁波(大约在 3 kHz 与 80 GHz 之间)。 可见光也是电磁波,但频率要高得多(400 THz 到 700 THz)。 所有电磁波在空气或真空中都以相同的速度(称为光速)传播,大约是 3e8 m/s。 由于传播速度相同,因此任何一种电磁波在一个完整的振荡(正弦波的一个完整周期)中传播的距离唯一取决于它的频率。 我们称这个距离为波长,用符号 \(\lambda\) 表示。 你可能以前见过这个公式:
其中 \(c\) 是光速,当 \(f\) 以 Hz 为单位, \(\lambda\) 以 m 为单位时一般设为 3e8。 在天线领域中以上关系尤其重要:为了接收特定载波频率 \(f\) 的信号,需要与其波长 \(\lambda\) 相匹配的天线, 通常天线长度需要是 \(\lambda/2\) 或 \(\lambda/4\)。 还需要记住,无论频率/波长如何,无线电波(携带的信息)始终以光速从发射机向接收机传播。 在计算传播延迟(信号在空中的时间)时,一个经验结论是光在一纳秒内大约行进一英尺,另一个经验结论是信号从地球到地球同步卫星走一个来回需要大约 0.25 秒。
接收机架构¶
上文“接收机”小节中的图展示了输入信号下变频并分解 I 和 Q , 这种机制被称为“直接转换(Direct Conversion)”或“零中频(Zero IF)”,射频频率会被直接转换到基带频率。 另一个选择是不降频,直接以足够快的采样速率来捕捉从 0 Hz 到采样率的 1/2 频率的所有内容。 这种策略被称为“直接采样(Direct Sampling)”或“直接射频(Direct RF)”,这需要非常昂贵的 ADC 芯片。 此外,还有一种曾经流行于旧型收音机的架构,名字叫做“超外差(Superheterodyne)”, 它不会降频到 0 Hz,而是降到某个中频(Intermediate Frequency,简称IF)处”。 此外,图中还出现了低噪声放大器(Low-Noise Amplifier,简称LNA),它是一个适用于极低功率输入的放大器。 以下是这三种架构的框图,请注意也存在这些架构的变体和混合体:
基带信号与带通信号¶
我们将以 0 Hz 为中心的信号称为“基带信号(Baseband)”。 相反,“带通信号”是指信号在远离 0 Hz 的某个频率上,它是为了无线传输而被向上移动过去的。 注意,没有“基带传输”的概念,因为基带信号只能是虚拟的。 基带信号正好以 0 Hz 为中心(如 载波和下变频 小节里第二张图的右侧部分),但 非常接近 0 Hz (如下图的两个信号)其实也仍被视为基带信号。 右图还示例了一个带通信号,它一个非常高的频率 \(f_c\) 为中心。
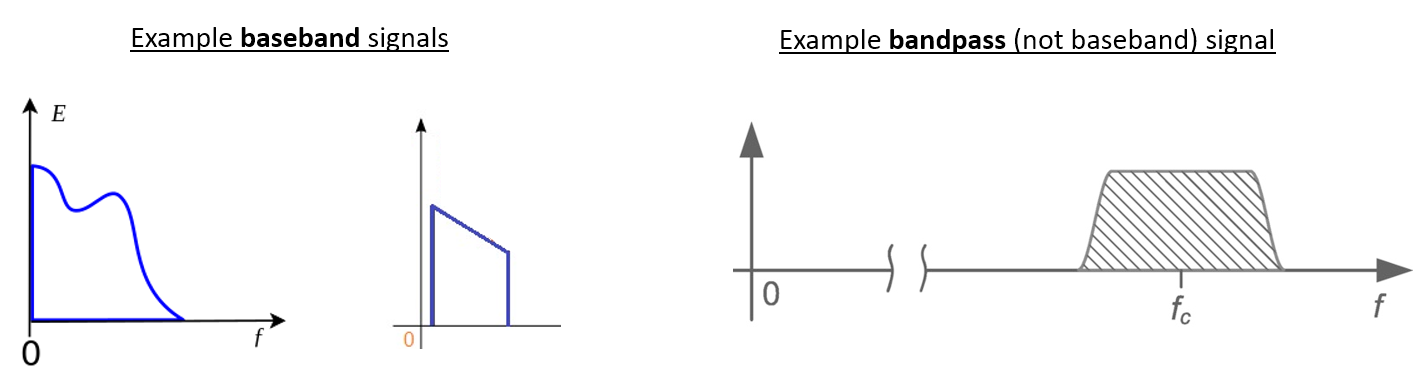
你可能看到过“中频(IF)”这个术语。目前,你只需把它看作基带信号和带通(射频)信号进行转换时的中间状态。
我们倾向于在基带处创建、记录、分析信号,因为这样可以以较低的采样率开展工作(出于前面小节讨论的原因)。 需要注意的是,基带信号通常是 复数 信号,而带通信号(比如我们实际上发射传输的无线电波)是 实数 信号。 仔细想一想这很合理:通过天线馈入的信号必须是实数,因为真实发射出去的无线电波的瞬时电压值只可能是实数。 若信号的 FFT 结果中负频率和正频率部分不完全相同,那么它一定是复数信号。 负频率不是真的意味着频率是负数,而是代表信号频率在载波频率以下。究其根本是我们发现用复数来记录信号(由此产生了正负频率)很方便。
如果我们的信号中没有任何虚部,那么我们就没有任何 Q 值(或者你可以认为所有的 Q 值都等于零)。 这反过来意味着我们只有没有任何相位偏移的余弦信号。 在频域中绘制时,由于具有相同的正负分量,没有相位偏移的余弦信号之和将关于 y 轴对称。
前文我们以 0.7-0.4j 作为复数举例过,实际上基带信号的采样点就会长成类似这样。 当你看到复数采样点(比如 IQ 采样点)时,它们大多数都是来自基带信号。 信号很少在射频处以数字方式表示或存储,因为这将制造大量的数据(采样率会非常高),并且我们通常只对射频频谱中的一小部分感兴趣。
直流峰值和偏移调节¶
当你开始使用 SDR 时,你经常会发现 FFT 的中心出现一个较大的峰值。 它被称为“直流峰值/偏置”或者“本振泄漏(LO Leakage)”, LO 是 SDR 设备内部的本地振荡器(Local Oscillator)的缩写。
下面是一个直流峰值的例子:
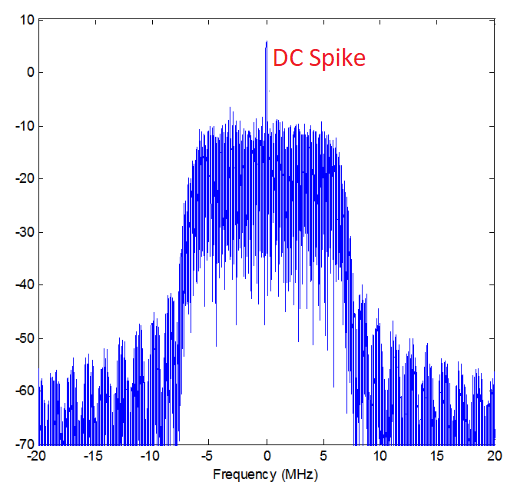
由于 SDR 会被调谐到中心频率,因此 FFT 的 0 Hz 对应的就是原带通信号的中心频率。 我们从而意识到,一个直流峰值(0 Hz 上的峰值)并不一定意味着原信号在此真有能量。 如果 FFT 只有一个直流峰值,而其余部分看起来像是噪声,那么实际上很可能并不存在真实的信号。
在“直接转换”机制的接收机中,直流偏置是常见问题, 大部分 SDR 设备(如 PlutoSDR、RTL-SDR、LimeSDR 和许多 Ettus USRP)都因此存在这个问题。 在直接转换接收机中,一个本振(LO)负责将信号从其实际频率下变频为基带信号。 因此,LO 泄漏会出现在下变频的结果的带宽中心。 LO 泄漏是通过频率组合产生的额外能量,但是消除这种额外噪声很困难,因为它靠近所需的输出信号。 许多射频集成电路(RFICs)内置了自动直流偏移消除功能,但通常需要存在真实的接收信号才能工作。 这就是为什么当不存在信号时,直流峰值会非常明显。
有一个简单而快速的方法可以解决这个问题,那就是调离中心频率并超采样(这个技巧被称为 Offset Tuning )。 举个例子,假设我们想在 100 MHz 的中心频率上查看 5 MHz 带宽的频谱(也就意味着采样率需要至少为 10MHz), 那么我们调离中心频率为 95 MHz ,同时以 20 MHz 的采样率超采样(这意味着能覆盖中心频率附近 10MHz 带宽的频谱)。
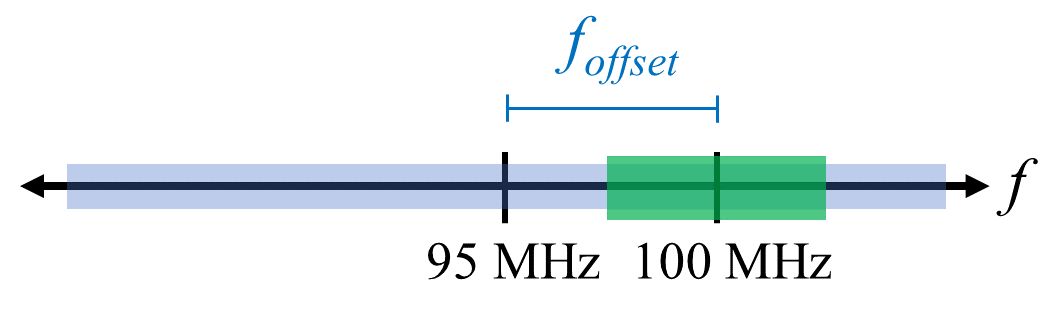
上图蓝色区域是 SDR 实际采样的范围,绿色区域是我们想要的频谱部分。 我们将 LO 即 SDR 的调谐频率设置为 95 MHz。 由于 95 MHz 位于绿色区域之外,因此在我们想要的频谱范围内不会出现任何直流峰值。
然而这会引发一个问题:如果我们希望接收以 100 MHz 为中心 5 MHz 宽度的信号, 则需要自己进行频率转移、滤波和下采样(后面我们将学习如何做到这一点)。 幸运的是,SDR 中通常已经内置了这种 LO 偏移功能(也称为 Offtuning),同时会将频率转移到用户所期望的中心频率。 这非常有用,因为我们通常使用 USB 或者以太网来连接计算机和 SDR,无法承受特别高的采样率。
本小节关于直流偏移的讨论很好地体现了本书与其他教材的侧重点不同。 一般的 DSP 教材虽然会讨论采样,但往往不会提及直流偏移这样的真实问题,尽管它们在实践中很常见。
计算平均功率¶
在进行 DSP 前首先应确定信号的存在性,为此人们常常会先计算信号的功率。 对于离散复信号,也就是我们常见的采样采样点点,我们可以通过求每个采样点的幅度的平方并求取平均来得到平均功率。
还记得吗,复数的“绝对值(模长)”就代表了这一点信号的幅度,即 \(\sqrt{I^2+Q^2}\) 。
使用 Python 计算平均功率代码是这样的:
avg_pwr = np.mean(np.abs(x)**2)
计算平均功率还有一个小妙招。 如果信号均值约等于 0 (SDR 设备采集的通常是这样,你稍后会看到为什么),那么信号功率可以通过计算采样点方差得到。 这种方法用 Python 写出来就是:
avg_pwr = np.var(x) # (信号的均值接近 0 才可以用这个方法)
为什么计算方差可以得到功率? 背后的数学原理其实很简单:\(\frac{1}{N}\sum^N_{n=1} |x[n]-\mu|^2\) , 其中 \(\mu\) 是信号的均值。 你会发现这个公式很眼熟!如果 \(\mu\) 是 0 ,那么计算方差的公式和计算平均功率的公式就等价了。 对于哪些均值不为 0 的采样点点而言,先减去它们的均值再求方差当然也行。 只需要记住,当信号均值不为 0 的时候,直接计算方差并不等于平均功率。
计算功率谱密度(PSD)¶
在上一章我们学过了通过 FFT 可以将信号从时域转换到频域,输出的结果其实就是功率谱密度(Power Spectral Density,缩写 PSD)。 许多 DSP 算法都是在频域中进行的,而 PSD 是一种可以将频域信息可视化的极有用的工具。 计算 PSD 并绘制出来并不容易,光有 FFT 是不够的,我们必须进行以下六个步骤来得到 PSD:
- 对采样点进行 FFT。如果我们有 x 个采样点,默认情况下 FFT 窗口大小就是 x。 举个例子,假设我们取一段信号的前 1024 个采样点作为 FFT 的输入,那么 FFT 窗口大小就是 1024,得到的输出就是 1024 个复数。
- 取 FFT 输出序列的幅度,得到 1024 个实数浮点数。
- 将得到的幅度平方,得到功率。
- 归一化:除以 FFT 大小( \(N\) )和采样率( \(Fs\) )。
- 单位转换为 dB: \(10 \log_{10}()\) ,记住我们总是以对数形式查看 PSD。
- 执行 FFT 移位(上一章已经介绍过):将“ 0Hz ”移到中心,将负频率移到中心的左边。
这六步用 Python 写出来是这样的:
Fs = 1e6 # 假设采样率是 100MHz
# 假设 x 就是我们得到的 IQ 形式的采样点序列
N = 1024
x = x[0:N] # 我们只拿出前 1024 个采样点进行 FFT, 参考下文
PSD = np.abs(np.fft.fft(x))**2 / (N*Fs)
PSD_log = 10.0*np.log10(PSD)
PSD_shifted = np.fft.fftshift(PSD_log)
我们可以选择加一个窗口函数作用,就像我们在 频率域 章节中学到的那样。
窗函数一般在 fft() 之前使用。
# 在 x = x[0:1024] 后加上这一行
x = x * np.hamming(len(x)) # Hamming 窗
绘制 PSD 图需要知道 x 轴的取值。 在上一章我们学过,对信号进行采样后只能“看到” \(-Fs/2\) 和 \(Fs/2\) 之间的频谱。 频域分辨率取决于 FFT 的窗口大小,其默认等于我们的输入采样点数。 在本例中,我们的 x 轴是 -0.5 MHz 和 0.5 MHz 之间均匀间隔的 1024 个点构成的。 如果我们将 SDR 调谐到 2.4 GHz,那么频谱上的观察窗口将为 2.3995 GHz 到 2.4005 GHz。 在 Python 中,获取观察窗口并移位的操作如下:
center_freq = 2.4e9 # SDR 的调谐频率
f = np.arange(Fs/-2.0, Fs/2.0, Fs/N) # 起始值,结束值,步长,中心为 0 Hz
f += center_freq # 每个值都加上中心频率(频谱整体移位)
plt.plot(f, PSD_shifted)
plt.show()
然后应该就能看到漂亮的 PSD 图像了!
如果你想要计算包含一百万个采样点点的 PSD,不要傻乎乎地直接把 FFT 窗口大小设置为一百万,因为这要花很长时间。 毕竟,它的输出会包含一百万个频率间隔(Frequency Bin),这太密了,画图都够呛。 相反,我建议进行多个较小的 PSD 并将它们平均化,或者使用时频谱来一起显示它们。 另外,如果你知道你的信号变化不快,只抽样其中几千个采样点来算 PSD 也可以。 在抽样区间内虽然只有几千个采样点),但可能也足够表示频谱特性了。
以下是一个包括信号(50 Hz 复指数信号)、噪声生成的完整代码示例。 注意,N 是用于模拟的采样点数,也是 FFT 窗口大小。
import numpy as np
import matplotlib.pyplot as plt
Fs = 300 # 采样率
Ts = 1/Fs # 采样间隔
N = 2048 # 用于模拟的采样点数
t = Ts*np.arange(N)
x = np.exp(1j*2*np.pi*50*t) # 模拟一个 50 Hz 的正弦信号
n = (np.random.randn(N) + 1j*np.random.randn(N))/np.sqrt(2) # 单位功率的复信号噪声
noise_power = 2
r = x + n * np.sqrt(noise_power)
PSD = np.abs(np.fft.fft(r))**2 / (N*Fs)
PSD_log = 10.0*np.log10(PSD)
PSD_shifted = np.fft.fftshift(PSD_log)
f = np.arange(Fs/-2.0, Fs/2.0, Fs/N) # 起始值,结束值,步长
plt.plot(f, PSD_shifted)
plt.xlabel("Frequency [Hz]")
plt.ylabel("Magnitude [dB]")
plt.grid(True)
plt.show()
输出:
