10. 多径衰落¶

在本章中，我们将学习多径（Multipath），它指的是信号从发射端 “经由两条或更多路径” 传播到接收端。这种现象才是真实场景中多见的，而我们之前所讨论的 “AWGN 信道” 只是一种简单地将信号加到噪声上的模型，基本上只适用于有线通信和一些卫星通信系统。

多径¶

无线信道中往往存在各种各样的 “反射体（Reflector）”，它们会反射射频信号。在发射机（TX）和接收机（RX）之间或附近的任何物体都会通过反射给原信号增加额外的传播路径，而每条路径都将制造不同的延迟（即相位变化）和衰减（即幅度变化）。来自所有路径的信号将在接收端叠加，这种叠加可能是相加性的（Constructively）、相消性的（Destructively）或者二者兼有。我们将信号通过多条信号路径到达接收端的概念称为 “多径”。在多径中，有一个路径是视线（Line-of-Sight, LOS）路径，而其他都是非视线路径。在下面的示例中，我们展示了一条 LOS 路径和一条非 LOS 路径：

在一些情况下，多径之间会产生相消性干涉。考虑上面的示例（其中只有两条路径），当载波频率或者路径距离变化时，来自这两条路径的信号可能以相似的幅度但是 180 度的相位差到达，这时它们会相互抵消（如下图所示）。当多径之间严重相消时，我们称之为 “深衰落（Deep Fade）”，此时接收端收到的信号会短暂消失。

多径之间的信号干涉也可以是相加性的，此时接收端信号相对于来自 LOS 路径的直射信号会得到增强。每条路径都有不同的相位偏移和幅度偏移，我们可以在时间域上的 “功率时延谱（Power Delay Profile）” 中可视化这些路径：

在功率时延谱中，最靠近 y 轴的箭头始终描述的是 LOS 路径（假设有的话），因为没有其他路径能比 LOS 路径更快到达接收端。通常，随着时延的增加功率会减小，因为信号到达接收端的路径距离会更远。

衰落¶

在现实情况下，接收端遇到的常常是相加性和相消性叠加的混合，这种混合还会随着接收端/发射端或环境的移动/变化而随时间改变。我们使用术语 “衰落（Fading）” 来描述多径信道的效应随时间的变化。所以宏观上我们用 “多径衰落（Multipath Fading）” 来描述这种现象，其本质是相加性/相消性干涉和变化环境的结合。多径衰落最终体现为接收端观察到一个随时间变化的信噪比（SNR）。这种变化的时间粒度通常在毫秒甚至微秒的量级上，具体取决于发射端/接收端移动的速度。下面是一个以毫秒为单位的时间轴上 SNR 随时间变化的图，展示了多径衰落的效果。

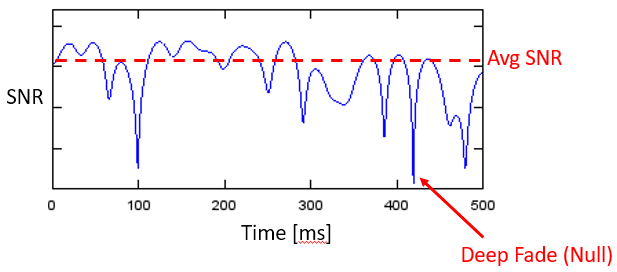
从时间域的角度看，多径衰落有两种类型：

慢衰落（Slow Fading）：信道在一个数据包的传输时间内基本上不改变。也就是说，若深衰落出现在慢衰落中，整个数据包都可能丢失。
快衰落（Fast Fading）：信道在一个数据包的传输时间内就会发生显著改变。前向纠错技术（Forward Error Correction）和交织（Interleaving）技术可以应对快衰落情况。

从频率域的角度看，多径衰落也能分成两种类型：

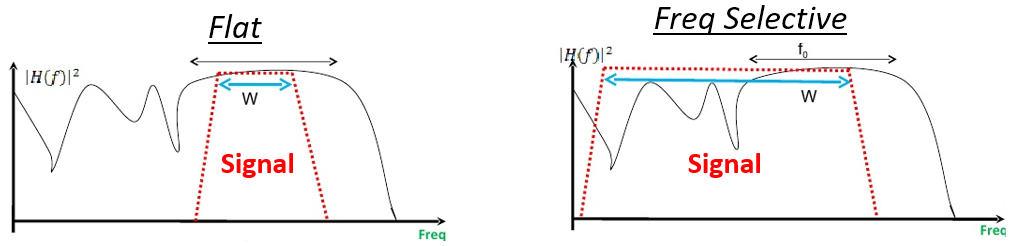
频率选择性衰落（Frequency Selective Fading） ：在我们所关注的信号频率范围内，多径导致的相加性/相消性叠加发生差异。举个例子，假设我们关注的是一个宽带信号，其频谱范围较大，也即波长范围较大。那么在这一较大范围内，不同波长经历的传播路径（信道）有较大不同，因而经历的多径衰落也各不相同，因此得名 “频率选择性衰落”。

平坦衰落（Flat Fading）：如果信号的带宽足够窄，以至于所有频率都经历大致相同的信道，那么此时的多径衰落可以称为平坦衰落。如果深衰落发生，那么在深衰落的时段内整个信号都将消失。

在下面的图中，红色形状显示了我们在频域中的信号，黑色曲线显示了不同频率下的信道条件。窄带信号的整个频谱体验到的是类似的信道条件，所以它经历的是平坦衰落。宽带信号则经历的是频率选择性衰落。

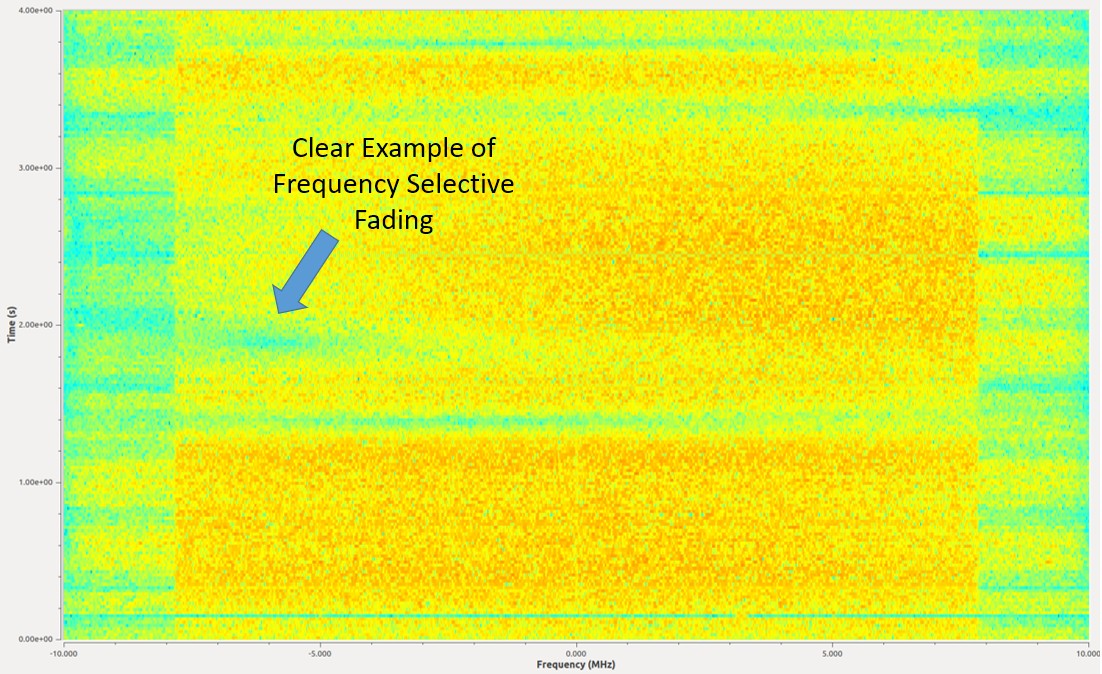
下图展示了一个频率选择性衰落的示例。图中，一个带宽为 16 MHz 的信号被传输，在某些时刻出现了因衰落导致的信号缺失。可以注意到，这些缺失是 “部分” 的，即在一些频率上导致了空洞但是没影响其他频率。

模拟瑞利衰落¶

当不存在一个信号较强的 LOS 路径时，瑞利衰落（Rayleigh Fading）模型可以被用来给多径衰落建模。当存在一个信号较强的 LOS 路径时，用莱斯衰落（Rician Fading）模型更合适。在此，我们主要关注瑞利衰落。瑞利/莱斯衰落模型并不包含发射端和接收端之间的主要路径损耗（比如链路预算中的路径损耗）或者大物体遮挡引起的损耗。它们的作用是模拟随时间变化的由于环境中的移动和散射物体引起的多径衰落。

基于瑞利衰落模型可以推导出许多理论，例如横越水平速率公式和平均衰落时长公式。然而，瑞利衰落模型并没有直接告诉我们如何实际使用该模型来进行信道仿真。要想仿真出瑞利衰落的信道，我们需要使用一些已发表的具体方法。下面的 Python 示例将使用克拉克的 “正弦和方法（sum-of-sinusoids method）” 来进行瑞利衰落的仿真。

在 Python 中生成瑞利衰落信道，首先需要指定最大多普勒频移（以 Hz 为单位）。当发射机和接收机的相对速度（表示为 $\Delta v$ ）远小于光速时（这往往成立），多普勒频移可以由以下公式计算：

$f_D = \frac{\Delta v f_c}{c}$

此处 $c$ 表示光速，约为 3e8 m/s，而 $f_c$ 表示发射机发出信号的载波频率。

我们还需要选择仿真所使用的正弦波的数量，这个取值来自于环境中散射体的数量（实际上我们无法知晓）所以没有标准答案。在计算中，我们假设通过每条路径到达接收端的信号的相位在 0 到 $2\pi$ 之间均匀随机。以下代码示例演示了使用克拉克方法模拟瑞利衰落：

import numpy as np
import matplotlib.pyplot as plt

# 仿真参数，你可以按照需求修改
v_mph = 60 # TX 与 RX 的相对速度，单位为 mile/h
center_freq = 200e6 # 载波频率，单位为 Hz
Fs = 1e5 # 采样率，单位为 Hz
N = 100 # 正弦波数量

v = v_mph * 0.44704 # 将 mile/h 转换为 m/s
fd = v*center_freq/3e8 # 最大多普勒频移
print("max Doppler shift:", fd)
t = np.arange(0, 1, 1/Fs) # 仿真时隙的数组 (start, stop, step)
x = np.zeros(len(t))
y = np.zeros(len(t))
for i in range(N):
    alpha = (np.random.rand() - 0.5) * 2 * np.pi
    phi = (np.random.rand() - 0.5) * 2 * np.pi
    x = x + np.random.randn() * np.cos(2 * np.pi * fd * t * np.cos(alpha) + phi)
    y = y + np.random.randn() * np.sin(2 * np.pi * fd * t * np.cos(alpha) + phi)

# z 是一个用以表示信道作用的复数参数，你可以把它看作是相位偏移加上幅度缩放
z = (1/np.sqrt(N)) * (x + 1j*y) # 信道仿真的核心公式
z_mag = np.abs(z) # 获取幅度，用以画图
z_mag_dB = 10*np.log10(z_mag) # 转换为 dB 表示

# 绘制 衰落-时间 变化图
plt.plot(t, z_mag_dB)
plt.plot([0, 1], [0, 0], ':r') # 0 dB
plt.legend(['Rayleigh Fading', 'No Fading'])
plt.axis([0, 1, -15, 5])
plt.show()

如果想把这个信道模型用于更大的仿真系统中，你只需要将接收到的信号乘以复数 z ，这个复数表示平坦衰落， z 的值在每个时隙中被更新。请注意，信号的所有频率成分在任何给定时刻都经历相同的信道，所以你无法仿真频率选择性衰落。仿真频率选择性衰落至少需要一个多时隙信道冲激响应，我们在本章暂不讨论。查看 z 的幅度变化，我们可以得到随时间变化的瑞利衰落：

从上图中可以看到两个有意思的点：一是深衰落会短暂出现，二是多径信道在某些时刻得到的接收信号甚至会比没有衰落的直射信号更好。

对抗多径衰落¶

在现代通信系统中，人们已经研究出了多种方法来对抗多径衰落的负面影响。

CDMA¶

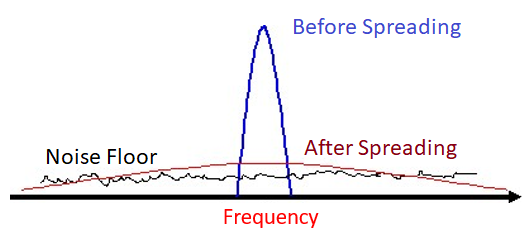
3G 蜂窝使用一种称为码分多址（CDMA）的技术。通过 CDMA，频谱较窄的原始信号在发送之前会使用直接序列扩频技术（DSSS）在更宽的频谱上进行扩展。在接收端，扩频过程被反转以恢复原始信号。如此一来，哪怕存在频率选择性衰落，多个不同的频率也不太可能同时出现深衰减。因此这种扩频-去扩频的过程能极大地避免深衰减造成信号丢失。

OFDM¶

正交频分复用（OFDM）是 4G 蜂窝、WiFi 等许多技术所使用的一种方案。 OFDM 使用所谓的 “子载波”（Subcarrier）在频域中将信号分成一堆互相存在交叉的窄信号。为了对抗多径衰落，我们可以避免将数据分配给处于深衰落中的子载波（当然，前提是接收端能快速向发射端告知当前信道状态）。我们也可以将高阶 QAM 调制方案分配给信道质量良好的子载波，以最大化我们的数据传输速率。