2. 频率域¶

在本章中，我们将学习频率域（Frequency Domain，后文简称频域）、傅里叶级数、傅里叶变换、傅里叶性质、快速傅里叶变换（FFT）、窗函数处理（Windowing）和时频谱/瀑布图（Spectrogram/Waterfall），同时还将学习 Python 实例分析。

学习数字信号处理（DSP）和无线通信的其中一个有趣的副产品是，能让你习惯于在频域中思考。然而，多数人对于频域的理解程度，可能仅限于在调节汽车音响的低音、中音和高音旋钮，或者简单的观察一个音频均衡器，如下图所示：

在本章结束时，你将深刻理解频域的真正含义，掌握如何在时间域（后文简称时域）和频域之间转换以及转换过程中的现象，并掌握一些在学习数字信号处理（DSP）和软件定义无线电（SDR）时常用的核心理论。在这本书结束时，我保证你将成为一个精通频域的大师！

首先，我们为何偏爱在频域中观察信号？这里有两个示例信号，通过在时域和频域的展示，我们可以一探究竟。

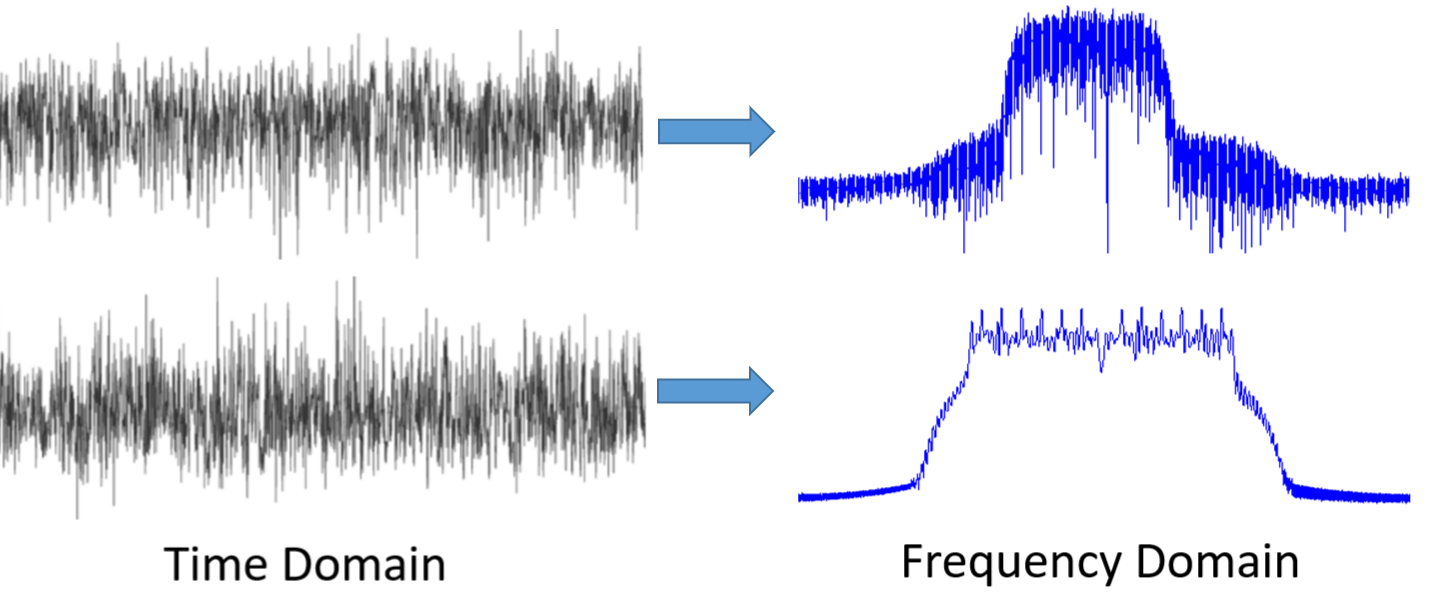
../_images/time_and_freq_domain_example_signals.png

就如你所见，在时域中，它们看起来就像是噪声，但在频域中我们就能观察到它们区别于众的特性！这就是一个事实：许多在时域中看起来相同普通的事物，其实有着不同的特征。我们通常所说的对信号进行“采样”，都是在时域下进行的，因为我们不能够在频域中直接进行信号采样。然而，有趣的事情往往发生在频域中。

傅里叶级数¶

频域的基本理念是任何信号都可以通过一系列叠加的正弦波来表达。如果我们将一个信号解构为其组成的正弦波，我们称之为傅里叶级数。以下是一个由两个正弦波组合构成的信号的示例：

Simple example of how a signal can be made up of multiple sinusoids, demonstrating the Fourier Series

下面是另一个例子，红色曲线通过累加多达 10 个正弦波来近似模拟一个锯齿波。我们可以看到这并不是一个完美的重建：由于锯齿波的锐利跳变，需要无限多的正弦波才能完全复原这个锯齿波：

Animation of the Fourier series decomposition of a triangle wave (a.k.a. sawtooth)

有些信号需要更多的正弦波来表达，有些甚至需要无限多，尽管它们总是可以用有限数量的正弦波来近似表示。这里是另一个信号被分解成一系列正弦波的例子：

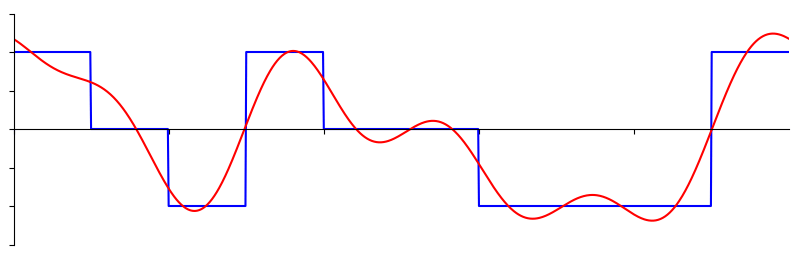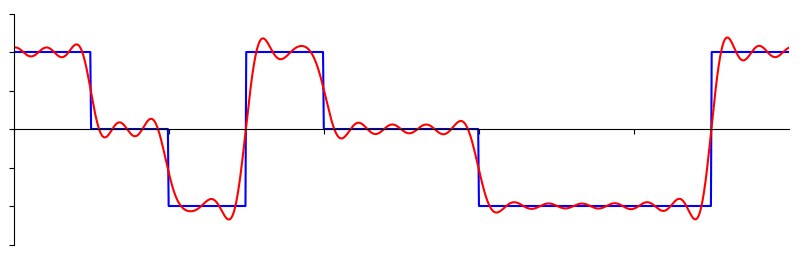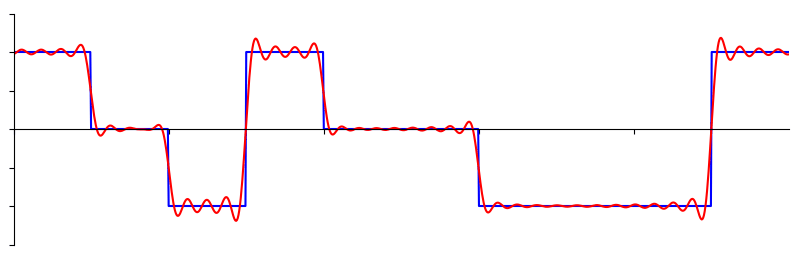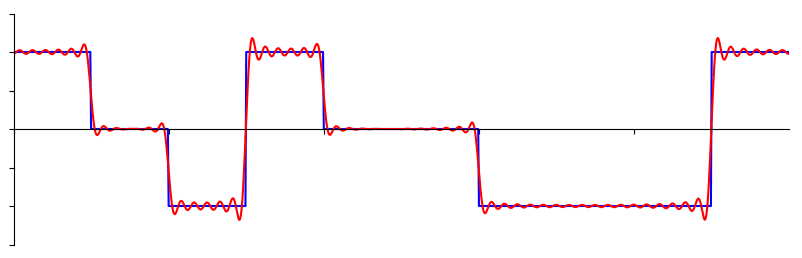
Animation of the Fourier series decomposition of an arbitrary function made up of square pulses

要理解我们如何将信号分解为正弦波（sine wave, 或称为 sinusoid），我们需要先回顾正弦波的三个属性：

幅度（Amplitude）
频率（Frequency）
相位（Phase）

幅度表示波的“强度”，而频率则是指每秒钟时长内完整波形的数量。相位用于表示正弦波在时间上的移动，范围从 0 到 360 度 (或 0 到 $2\pi$ ) ，但它必须相对于某物才有意义，比如两个频率相同的信号可能会相差 30 度的相位。

Reference diagram of amplitude, phase, and frequency of a sine wave (a.k.a. sinusoid)

此时，你或许已经意识到了“信号”本质上就是一个函数，通常是在“时间”这个轴（即 x 轴）上来表示的。另外一个容易记忆的特性是周期，它是频率的倒数。正弦波的周期是波完成一个循环所需的时间，单位是秒。因此，频率的单位是 1/秒，或者赫兹（Hz）。

当我们将信号分解为一系列的正弦波时，每一个波都会有一定的幅度、相位和频率。每个正弦波的幅度将告诉我们原始信号中该频率的强度。先不用过多担心相位，其实你只需意识到 $sin()$ 和 $cos()$ 之间唯一的区别就是一个相位移动（时间位移）。

理解概念比解决傅里叶级数的实际方程更重要，但是对于那些对方程感兴趣的人，我推荐他们参考 Wolfram 的简洁解释：https://mathworld.wolfram.com/FourierSeries.html。

时间-频率对¶

我们已经确定信号可以表示为正弦波，它具有若干特性。现在，我们将学习如何在频域中绘制信号。时域展示了信号随时间的变化，而频域显示了信号在哪些频率中占据了多少份额。在频谱图中，x 轴不再是时间而是频率。我们可以同时在时域和频域中绘制一个给定的信号。让我们从一些简单的例子开始。

下面是一个频率为 $f$ 的正弦波，在时域和频域中的样子：

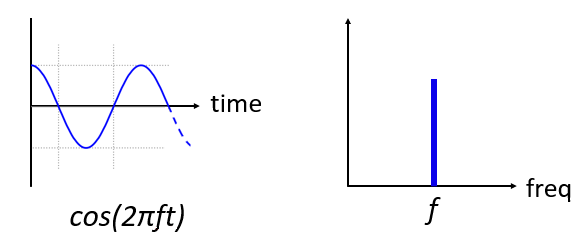
The time-frequency Fourier pair of a sine wave, which is an impulse in the frequency domain

时域图应该看起来非常熟悉，它是一个振荡函数。不用担心它在周期中的启动点或持续的时间长短。关键点是信号只有一个 单一频率 ，这也是为什么我们在频谱图中看到一个单一的尖峰。正弦波在哪个频率上振荡，在频谱图中就会在哪个位置看到尖峰。数学上对这样的尖峰的专业术语叫做“冲激”。

那么如果我们在时域图中有一个冲激会怎样呢？试想录音中有人拍手或者用锤子钉钉子的声音。这时，时频对应关系就不那么直观了。

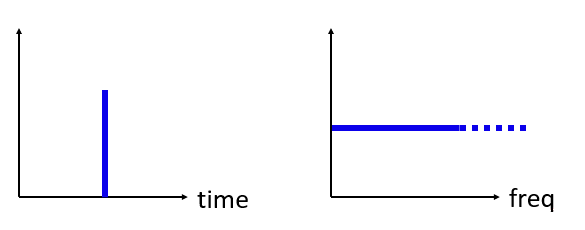
The time-frequency Fourier pair of an impulse in the time domain, which is a horizontal line (all frequencies) in the frequency domain

如我们所见，在时域中的冲激在频域中却是扁平的，也就是说它含有几乎每一个频率。没有理论上完美的冲激，因为这意味着它必须在时域中无限短。就像正弦波一样，冲激在时域中发生的位置并不重要。这里只需要重点理解：时域中的快速变化意味着大量不同频率的杂糅。

接下来，让我们看一下方波在时域和频域中的图像：

The time-frequency Fourier pair of a square wave, which is a sinc (sin(x)/x function) in the frequency domain

这个的频谱图同样也不太直观。我们可以看到频域中有一个强烈的尖峰恰好出现在方波的频率上，而随着频率的提高还会出现更多的尖峰。这是因为像上一个例子中所说，时域中的快速变化意味着杂糅的大量不同频率。它们以一定的间隔出现尖峰，而且强度会慢慢衰减（这个衰减过程会无限进行下去）。时域中的方波，在频域中呈现出 $sin(x)/x$ 的形态（也就是所谓的 $sinc$ 函数）。

那么如果我们在时域有一个恒定的信号会怎样呢？答案是：恒定的信号没有“频率”，我们一起来看看：

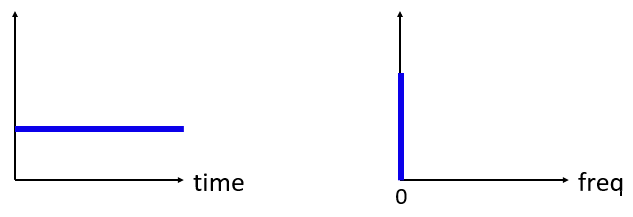
The time-frequency Fourier pair of a DC signal, which is an impulse at 0 Hz in the frequency domain

在频域中，我们会在 0 Hz 位置看到一个峰值，这是由于即使“无”频率，频域也不会真正的“空白”。这种情况只会在没有信号存在的情况下出现，例如在时域中所有值都为 0。我们通常将频域中的 0 Hz 称为“直流（DC）”，这是由于它由时域中的直流信号（一个恒定且不变的信号）产生的。值得注意的是，当我们增加时域中直流信号的幅度时，频域中在 0 Hz 处的峰值也会相应地增加。

在后续的学习过程中，我们会详细讲解频谱图中纵坐标的具体含义。但现在，你可以把它看作是某种幅度，这个幅度反映了时域信号中某频率成分的强度。

傅里叶变换¶

数学上，傅里叶变换（Fourier Transform）是一种时域到频域的 “变换”。其定义如下：

$X(f) = \int x(t) e^{-j2\pi ft} dt$

为信号 $x(t)$ 我们可以使用下面的公式得到其频域版本 $X(f)$ 。我们将以 $x(t)$ 或 $y(t)$ 来表示函数的时域版本，相应的以 $X(f)$ 和 $Y(f)$ 来表示其频域版本。注意“ $t$ ”代表时间，而“ $f$ ”代表频率。“ $j$ ”只是虚数单位而已。你可能在高中数学课上见过用“ $i$ ”来表示它。在工程和计算机科学中使用“ $j$ ”，因为在这些领域中“ $i$ ”通常指电流，并且在编程中常常作为循环变量使用。

要从频域返回到时域几乎是一样的，除了多了一个缩放因子和一个负号：

$x(t) = \frac{1}{2 \pi} \int X(f) e^{j2\pi ft} df$

请注意，许多教科书和其他资源使用 $w$ 代替 $2\pi f$ 。 $w$ 是以弧度每秒为单位的角频率，而 $f$ 是以 Hz 为单位。你只需要知道：

$\omega = 2 \pi f$

即使它在许多方程中增加了一个 $2 \pi$ 项，在实际中我们更倾向于使用频率的 Hz 单位。最终，你在 SDR 应用中使用的将是 Hz 单位。

上述傅里叶变换的方程是连续形式，其实你只会在数学问题中看到它。离散形式的方程才更接近于它在代码中实现的形态：

$X_k = \sum_{n=0}^{N-1} x_n e^{-\frac{j2\pi}{N}kn}$

请注意，主要区别在于我们用求和替换了积分。指标 $k$ 从 0 到 N-1。

如果这些方程对你来说没有多大意义，也没关系。实际上，我们不直接使用它们也可以用 DSP 和 SDR 做一些很酷的事情！

时间-频率性质¶

我们之前检查了信号在时域和频率域中的表现形式的例子。现在，我们将涵盖五个重要的“傅里叶性质”。这些性质告诉我们，如果我们对时域信号做 ____ ，那么 ____ 将发生在频域信号上。这将给我们一些重要的深入了解，关乎实践中我们将对时域信号执行的 DSP。

线性性质:

$a x(t) + b y(t) \leftrightarrow a X(f) + b Y(f)$

这个特性可能是最容易理解的。如果我们在时间上加总两个信号，那么在频域中对应的也会是两个频域信号的加和。这也告诉我们，如果我们将其中一个信号乘以一个缩放因子，频域中的表示也会相同比例地缩放。这个特性的实用性会在我们加总多个信号时变得更加明显。

频移性质:

$e^{2 \pi j f_0 t}x(t) \leftrightarrow X(f-f_0)$

$x(t)$ 左边的项我们称之为”复数正弦波”或”复数指数”。目前，我们所需要知道的是，它本质上就是一个频率为 $f_0$ 的正弦波。这个属性告诉我们，如果我们将一个信号 $x(t)$ 与一个正弦波相乘，那么在频率域我们得到的是 $X(f)$ ，只是频率偏移了一定的 $f_0$ 。这种频偏用可视化可能更好展现：

Depiction of a frequency shift of a signal in the frequency domain

频移操作对于 DSP 应用来说是非常重要的，因为我们出于多种原因需要将信号在频率上进行上移或下移。这个性质告诉我们如何去实现（通过乘以一个正弦波）。这里是另一种可视化这个性质的方法：

Visualization of a frequency shift by multiplying by a sine wave or sinusoid

时域缩放性质:

$x(at) \leftrightarrow X\left(\frac{f}{a}\right)$

在方程的左边，我们可以看到在时域中对我们的信号 $x(t)$ 进行了缩放。这里有一个信号在时间上缩放的例子，我们看看频域上发生了什么变化：

Depiction of the time scaling Fourier transform property in both time and frequency domain

时域上的缩放本质上是在 x 轴上缩小或扩展信号。这一属性告诉我们，在时域上的缩放会导致在频域上的逆向缩放！例如，当我们更快地传输比特流时，结果是使用了更大的带宽。这一属性有助于解释为什么更高数据率的信号会占用更多的带宽/频谱资源。如果时频缩放是成正比而不是成反比的，那么蜂窝运营商可以以超快速度传输数据，还不用为频谱支付数十亿美元！不幸的是，情况并非如此。

已经熟悉这个属性的人可能会注意到这里缺少一个缩放因子：为了简单起见，它被省略了，而且在实际应用中这没有区别。

时域卷积性质:

$\int x(\tau) y(t-\tau) d\tau \leftrightarrow X(f)Y(f)$

因为我们考察的是在时域中将 $x(t)$ 与 $y(t)$ 进行卷积后的性质，所以称之为卷积性质。你可能还不知道卷积操作是什么，姑且将它想象成一种互相关运算吧，我们将在这一章更深入地探讨卷积。当我们在时域对信号进行卷积时，其等效于在频率域将那两个信号相乘。这与将两个信号相加非常不同。当你将两个信号相加时，如我们所见，实质上没有什么变化，你只是简单地将它们的频率域版本相加在一起。但是当你将两个信号卷积时，就好像从它们创建了一个新的第三个信号。卷积是数字信号处理（DSP）中最重要的技术，尽管我们必须先理解滤波器的工作原理才能完全掌握它。

在我们继续前进之前，先简要解释一下这个性质为什么这么重要。请考虑这样一种情况：你有一个想要接收的信号，而旁边就有一个干扰信号。

掩码（masking）在编程中的应用非常广泛，我们在这里就利用一下这个概念。如果我们能创建下面的掩码，并将其与上方的信号相乘，以便屏蔽我们不想要的信号，那会怎样？

我们通常在时域进行 DSP 操作，那么我们利用时域卷积性质来看看如何在频域进行这种掩码。假设 $x(t)$ 是我们接收到的信号。 $Y(f)$ 是我们想要在频域应用的掩码， $y(t)$ 是我们掩膜的时域表示，如果我们将它与 $x(t)$ 进行卷积，我们就可以“过滤掉”我们不想要的信号。

Figure made with TikZ

当我们讨论过滤需求时，这个时域卷积性质就很有用了。

频域卷积性质:

最后，我想指出卷积特性反过来也是成立的，尽管我们不会像使用时域卷积那样频繁地使用它：

$x(t)y(t) \leftrightarrow \int X(g) Y(f-g) dg$

其实还有很多其他性质，但在我看来上述五个是最关键的。我们没有逐一推敲每个性质的推导证明，但是，关键点在于我们使用这些数学性质来进行信号分析处理时，真实信号会发生什么改变。不用纠结于数学公式，确保自己理解了每个性质到底意味着什么就足够了。

快速傅里叶变换（FFT）¶

现在回到傅里叶变换（Fourier Transform）。我已经给你展示过了离散傅里叶变换的公式，但其实在 99.9% 的编码场景下用的都是 FFT 函数，即 fft()。快速傅里叶变换是离散傅里叶变换的一种实现算法，自几十年前发展起来后，即便离散傅里叶变换有许多不同的实现方式，FFT 仍是首选。事实上，从其以“ F ”（Fast，快速）作为首字母的命名就可以看出其效率之高！

FFT 是一个单输入单输出的函数。它负责将信号从时域转换到频域。

FFT is a function with one input (time domain) and one output (frequency domain)

在这本书中，我们将仅关注一维的 FFT（二维 FFT 用于图像处理及其他应用中）。在我们将在本书中讨论的案例里，FFT 函数会有一个输入（即样本向量），并输出另一个向量（输入样本向量在频域中的表达方式）。输出向量的长度总是与输入向量的长度一致。例如，如果我向 FFT 输入了 1024 个样本，那么我就会得到 1024 个输出样本。 FFT 令人疑惑的一点在于，其输出总是在频域中的，所以当我们试图绘制输出向量的时候，我们会发现在 x 轴上的“范围”并不会随着在时域中样本数量的变化而变化。我们可以通过观察输入和输出数组及其索引来可视化说明这一点：

Reference diagram for the input (seconds) and output (bandwidth) format of the FFT function showing frequency bins and delta-t and delta-f

由于输出是在频域中，所以 x 轴的范围只取决于采样率，我们将在下一章节中详细介绍这一点。当我们使用更多的样本来构成输入向量时，我们可以在频域中获得更好的分辨率（除了同时处理更多的样本之外）。通过增加输入的大小，我们实际上并不能“看到”更多的频率。唯一能“看到”更多频率的方法是提高采样率（即减小采样周期 $\Delta t$ ）。

如何可视化 FFT 的输出呢？我们举个例子来说明。假设我们的采样率是每秒一百万个样本点（1 MHz），那么在 FFT 输出中我们只能看到最高 0.5 MHz 的信号（我们将在下一章学到原因），而无论向FFT的输入增加多少样本都不会改变这一点。FFT 的输出性质可以抽象如下：

其输出显示的频率范围总是从 $\text{-} f_s/2$ 到 $f_s/2$ ，其中 $f_s$ 代表采样率。即，输出总会有负频率部分和正频率部分。如果输入是复信号，负频率部分和正频率部分会不同；如果输入是实信号，这两部分则会相同。

至于上图横轴的单位长，即每个频率间隔（frequency bin）对应的是 $f_s/N$ 赫兹。也就是说，向每个 FFT 提供更多的样本可以让输出的分辨率更细。如果你刚开始接触这个领域，这是一个可以忽略的细节。数学上，最后一个索引并不完全对应 $f_s/2$ ，而是 $f_s/2 - f_s/N$ 。对于很大的 $N$ 而言，可以视其近似为 $f_s/2$ 。

负频率¶

那么负频率又是什么呢？目前，你只需要记住它们与使用复数（虚数）有关：在传输/接收射频（RF）信号时，实际上并不存在物理意义上的“负频率”，这只是我们创造的一种表示方法。为了让你能直观理解它的意义：假设我们将SDR接收设备的中心频率调到 100 MHz（常见的 FM 广播频段）并以 10 MHz 的速率采样，我们将可以观察到 95 MHz 至 105 MHz 的频谱，假设现在频谱上有三个信号存在：

那么，SDR给我们的样本实际上看起来会是这样：

Negative frequencies are simply the frequencies below the center (a.k.a. carrier) frequency that the radio tuned to

虽然接收信号的中心频率被调到了 100MHz，但是在接受结果中，97.5 MHz 的信号实际会显示为 -2.5 MHz，负频率出现了！但是实际上，仅仅是因为它低于中心频率而已。当我们学习更多关于采样的知识并且积累了 SDR 设备的使用经验后，你将彻底明白为什么会发生这个转换。

时域中的顺序并不重要¶

在我们开始深入探讨 FFT 之前，还有最后一个性质需要了解。 FFT 函数的行为有点像将输入从时域上压扁然后吐出一个频域上的结论，同时这个频域的结果会具备不同的分量和尺度。也就是说，FFT的输出已经“跳出”了时间维度！有一个很好的角度可以帮你深刻理解这一点：在时域中改变事件发生的顺序并不会改变信号中的频率成分。也就是说，下面两个信号的 FFT 输出将都有相同的两个峰值，因为信号只是不同频率的两个正弦波。改变正弦波发生的顺序并不改变它们是不同频率的两个正弦波这一频域上的事实。

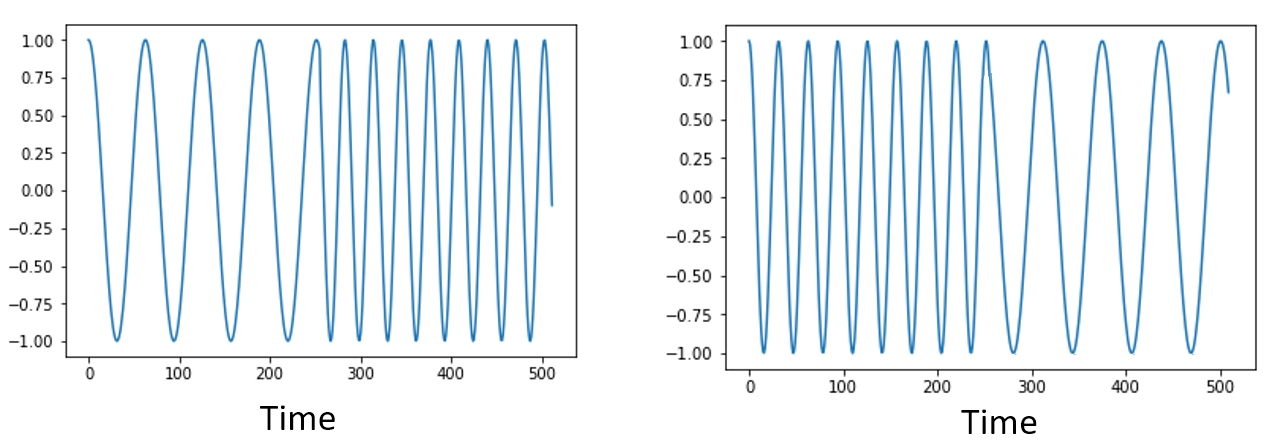
When performing an FFT on a set of samples, the order in time that different frequencies occurred within those samples doesn't change the resulting FFT output

理论上而言，由于时域上正弦波的相位也能不同，FFT 输出的相位也会跟着发生变化。然而，在本书的前几个章节中，我们暂且仅关注 FFT 输出的幅度。

在 Python 中使用 FFT¶

在了解了 FFT 的理论和性质后，现在让我们来看一些 Python 代码并实操 NumPy 的 FFT 函数：np.fft.fft() 。建议你在自己的电脑上使用 Python 控制台或者 IDE 软件跟随操作，但如果实在不方便，你也可以暂时使用导航栏左侧底部链接的在线 Python 控制台。

首先我们需要在时域创建一个信号。你可以在你的 Python 控制台中跟着做。为了简化问题，我们将制造一个 0.15 Hz 的简单正弦波。我们还将使用 1 Hz 的采样率，也就是说我们在 0 秒、1 秒、2 秒、3 秒等时间点进行采样。

import numpy as np
t = np.arange(100)
s = np.sin(0.15*2*np.pi*t)

如果我们绘制 s ，它将看起来像这样：

接下来，让我们使用 NumPy 中的 FFT 函数：

S = np.fft.fft(s)

如果我们打印 S ，将会看到它是一个复数数组：

S =  array([-0.01865008 +0.00000000e+00j, -0.01171553 -2.79073782e-01j,0.02526446 -8.82681208e-01j,  3.50536075 -4.71354150e+01j, -0.15045671 +1.31884375e+00j, -0.10769903 +7.10452463e-01j, -0.09435855 +5.01303240e-01j, -0.08808671 +3.92187956e-01j, -0.08454414 +3.23828386e-01j, -0.08231753 +2.76337148e-01j, -0.08081535 +2.41078885e-01j, -0.07974909 +2.13663710e-01j,...

一个提示：无论你在何时何地遇到了复数，请尝试计算其幅度和相位看看能否得到一些有意义的信息。在大多数编程语言中，abs() 是用来计算复数幅度的函数，而计算相位的函数各不相同，在 Python 中它是 np.angle()。让我们画出来看看：

import matplotlib.pyplot as plt
S_mag = np.abs(S)
S_phase = np.angle(S)
plt.plot(t,S_mag,'.-')
plt.plot(t,S_phase,'.-')

目前我们没有为这个图提供任何 x 轴信息，它仅仅是数组的索引（从 0 开始计数）。基于数学原因，FFT 的输出具有以下格式：

Arrangement of the output of an FFT before doing an FFT shift

但我们想要将 0 Hz（直流）放在中心，负频率放在左边（这是这个领域中大家喜欢的可视化习惯）。因此，任何时候算完 FFT 都会跟着进行一次“ FFT shift ”，实际上就是一个简单的数组重新排列操作，有点像循环移位，说白了就是“把这个摆在这里，那个挪过去”。下面的图示完整地定义了 FFT shift 操作做了什么：

Reference diagram of the FFT shift function, showing positive and negative frequencies and DC

好消息是，NumPy 内置了 FFT shift 函数：np.fft.fftshift()。我们只需要将 np.fft.fft() 这行替换为：

S = np.fft.fftshift(np.fft.fft(s))

我们还需要确定 x 轴的数值/标签。回想一下，之前为了简化问题，我们使用了 1 Hz 的采样率。这意味着频率域图的左边缘是 -0.5 Hz，右边缘是 0.5 Hz （如果你暂时不知道为何也没关系，当你看完关于采样的章节 IQ 采样之后就会明白了）。我们先记住采样率为 1 Hz 的假定，并且用正确的 x 轴标签来绘制FFT输出的幅度和相位图。下面是这个 Python 示例的最终版本以及输出结果：

import numpy as np
import matplotlib.pyplot as plt

Fs = 1 # Hz
N = 100 # 用于处理的样本点数量，同时也等于我们的 FFT 窗口大小

t = np.arange(N) # 因为采样率是 1 Hz
s = np.sin(0.15*2*np.pi*t)
S = np.fft.fftshift(np.fft.fft(s))
S_mag = np.abs(S)
S_phase = np.angle(S)
f = np.arange(Fs/-2, Fs/2, Fs/N)
plt.figure(0)
plt.plot(f, S_mag,'.-')
plt.figure(1)
plt.plot(f, S_phase,'.-')
plt.show()

请注意，我们在 0.15 Hz 处看到了峰值，这正是我们在创建正弦波时使用的频率，这意味着我们的 FFT 算法有效！在现实情况中，我们可能并不知道一段信号的生成代码，而只拿到了它的样本数据，那么也同样可以使用 FFT 来确定它的频率。我们在 -0.15 Hz 处也看到一个峰值的原因是它是一个实信号而不是复信号，我们稍后会更深入地讨论这个问题。

窗函数处理¶

当我们使用 FFT 来测量我们信号的频率分量时，背后的数学前提是这个信号是 周期性 信号的一部分。它预期着我们提供的信号片段无限期地重复下去。就好像信号片段的最后一个样本与第一个样本相连。这是源于傅里叶变换背后的数学理论。这意味着我们希望避免第一个样本与最后一个样本之间的突变，因为在时域中的突变会造成频域上大量混杂的峰值，而实际上我们的最后一个样本并不真正与第一个样本相连。简单来说：如果我们要对100个样本进行FFT，使用 np.fft.fft(x) ，我们希望能使得 x[0] 和 x[99] 的值相等或接近。

我们通过“窗函数处理（Windowing）”来支持这种循环特性。在进行 FFT 之前，我们会将信号片段与窗函数（Window Function）相乘，窗函数是任何在两端衰减至零的函数。这确保了信号片段在相乘后将从零开始并在零结束，从而能够相互连接。常见的窗函数包括汉明（Hamming）窗、汉宁（Hanning）窗、布莱克曼（Blackman）窗和凯撒（Kaiser）窗。当你不应用任何窗函数时，这称为使用了“矩形”窗，因为它就像乘以一系列的 1。这里展示了几种窗函数的样子：

Windowing function in time and frequency domain of rectangular, hamming, hanning, bartlet, blackman, and kaiser windows

对于初学者来说，可以直接选择 Hamming 窗。在 Python 中可以通过 np.hamming(N) 来创建，其中 N 是数组中的元素数量，也就是代码中的 FFT 窗口大小（size）。为了在 FFT 之前应用窗函数处理，仅需在上文第二行代码之后插入：

s = s * np.hamming(100)

如果你担心选择错误的窗函数，请不用担心。 Hamming 窗、Hanning 窗、Blackman 窗和 Kaiser 窗之间的区别与完全不使用窗函数的代价相比是非常小的，因为它们都在两侧逐渐趋于零，都解决了最主要的问题。

FFT 窗口大小设置¶

需要注意的最后一点是 FFT 的窗口大小设置。最佳的 FFT 窗口大小（FFT size）总是2的幂次方，这根植于 FFT 背后的实现方式。你也可以使用不是2的幂次方的窗口大小，但这样会慢一些。常见的窗口大小在 128 到 4,096 之间，当然你也可以选择更大的尺寸。实际操作中，我们可能需要处理长达数百万甚至数十亿采样的信号，所以我们需要将信号分割并执行多次 FFT。这意味着我们将获得很多输出。我们可以选择对它们求平均或者随时间变化绘制它们的图像（特别是当信号随时间变化时）。你不必将信号的 每一个 样本都通过 FFT 处理也足以获得一个良好的频域表征。例如，即使你只从每 100k 个样本中选取 1,024 个样本进行 FFT，只要目标信号是连续的，得到的结果通常也是可以接受的。

时频谱/瀑布图¶

时频谱（Spectrogram）是显示一段时间跨度内的频率变化的图形。这实际上就是将一堆 FFT 输出垂直堆叠起来（如果你想要频率显示在水平轴上的话）。我们也可以实时显示它，后者通常被称为瀑布图（Waterfall）。频谱分析仪（spectrum analyzer）是用来显示这种瀑布图的设备。下面的图表展示了如何将一串 IQ 样本切割成时频谱的形式：

Spectrogram (a.k.a. waterfall) diagram showing how FFT slices are arrange/stacked to form a time-frequency plot

由于时频谱是由一堆二维数据（FFT 输出）拼接而成的，所以它实际上是一个三维图，因此我们必须使用颜色映射来表示 FFT 的强度（即使用不同的颜色来展示第三个维度），这些强度是我们想要绘制的“数值”。这里是一个时频谱的示例，频率在水平方向（x 轴）上，时间在垂直方向（y 轴）上。蓝色代表最低能量，而红色是最高能量。我们可以看到，在中心处 DC（0 Hz）有一个强烈的尖峰，周围有一个变化的信号。蓝色代表背景底噪。

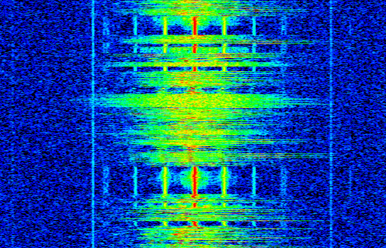
请记住，这只是一系列 FFT 输出的叠加，每行都是一次 FFT（严格来说，是一次 FFT 输出的幅度值）。确保将输入信号切分成与 FFT 窗口大小（例如，每个切片包含 1024 个样本，然后一行就表示过去了 1024 个样本的时间）相匹配的时间片段。

在我们开始编写产生时频谱代码之前，这里有一个示例信号供我们使用，这是一个嵌入在白噪声中的单一频率的音调：

import numpy as np
import matplotlib.pyplot as plt

sample_rate = 1e6

# 生成目标信号并叠加白噪声
t = np.arange(1024*1000)/sample_rate # 时间轴
f = 50e3 # 示例信号的频率
x = np.sin(2*np.pi*f*t) + 0.2*np.random.randn(len(t))

这是它在时域中的样子（前 200 个样本）：

在 Python 中，我们可以这样生成时频谱：

# 模拟上文生成的信号，或者你自己生成的信号

fft_size = 1024
num_rows = len(x) // fft_size # // 是带取整的除法算子
spectrogram = np.zeros((num_rows, fft_size))
for i in range(num_rows):
    spectrogram[i,:] = 10*np.log10(np.abs(np.fft.fftshift(np.fft.fft(x[i*fft_size:(i+1)*fft_size])))**2)

plt.imshow(spectrogram, aspect='auto', extent = [sample_rate/-2/1e6, sample_rate/2/1e6, 0, len(x)/sample_rate])
plt.xlabel("Frequency [MHz]")
plt.ylabel("Time [s]")
plt.show()

该操作应会生成以下结果，这算不上一个很有趣的时频谱，因为没有频率时变行为。它有两个音调是因为我们模拟了一个真实信号，而真实信号总是有一个与正侧相匹配的负功率谱密度（PSD）。想看更多有趣的时频谱示例，请访问 https://www.IQEngine.org！

FFT 的代码实现¶

即使 NumPy 已经为我们内置了 FFT 函数，但了解一下其内部工作原理还是很有益的。最流行的 FFT 算法是 Cooley-Tukey FFT 算法，它最初由 Carl Friedrich Gauss 于大约 1805 年发明，然后在 1965 年被 James Cooley 和 John Tukey 重新发明并普及。

这个算法的基本版本适用于二的幂次方窗口大小的 FFT，旨在处理复数输入，但也可以处理实数输入。这个算法的构建模块被称为蝶形运算（Butterfly），本质上是一个 N = 2 窗口大小的 FFT，包括两次乘法运算和两次求和运算：

Cooley-Tukey FFT algorithm butterfly radix-2

即

$y_0 = x_0 + x_1 w^k_N y_1 = x_0 - x_1 w^k_N$

其中 $w^k_N = e^{j2\pi k/N}$ 被称为旋转因子（ $N$ 是 FFT 窗口大小， $k$ 是索引）。注意输入和输出都是复数，例如， $x_0$ 可能是 0.6123 - 0.5213j，加法与乘法操作都是复数运算。

该算法是二分递归的，直到最后只剩下一系列的蝶形运算，下面用一个窗口大小为 8 的 FFT 来描述这个过程：

此模式中的每列都是一组可以并行执行的操作，总共执行了 $log_2(N)$ 步，这就是为什么 FFT 计算复杂度是 $O(N\log N)$ ，而 DFT 是 $O(N^2)$ 。

对于那些喜欢用代码而不是方程来思考的人来说，下面为你展示了一个简单的 FFT 的 Python 实现，以及一个由音调加噪声组成的示例信号，你可以用它来尝试运行 FFT。。

import numpy as np
import matplotlib.pyplot as plt

def fft(x):
    N = len(x)
    if N == 1:
        return x
    twiddle_factors = np.exp(-2j * np.pi * np.arange(N//2) / N)
    x_even = fft(x[::2]) # 递归是一种神奇的编程技巧quq
    x_odd = fft(x[1::2])
    return np.concatenate([x_even + twiddle_factors * x_odd,
                           x_even - twiddle_factors * x_odd])

# 模拟音调加噪声
sample_rate = 1e6
f_offset = 0.2e6 # 与载波相偏 200 kHz
N = 1024
t = np.arange(N)/sample_rate
s = np.exp(2j*np.pi*f_offset*t)
n = (np.random.randn(N) + 1j*np.random.randn(N))/np.sqrt(2) # 单位复数噪声
r = s + n # 0 dB SNR

# 执行 fft, fftshift, 转换为 dB 表示
X = fft(r)
X_shifted = np.roll(X, N//2) # 等价于 np.fft.fftshift
X_mag = 10*np.log10(np.abs(X_shifted)**2)

# 绘图
f = np.linspace(sample_rate/-2, sample_rate/2, N)/1e6 # 以 MHz 为单位
plt.plot(f, X_mag)
plt.plot(f[np.argmax(X_mag)], np.max(X_mag), 'rx') # 展示最大值
plt.grid()
plt.xlabel('Frequency [MHz]')
plt.ylabel('Magnitude [dB]')
plt.show()

对于那些对 JavaScript 和/或 WebAssembly 的实现感兴趣的人来说，可以查看 WebFFT 库，它用于在 Web 或 NodeJS 应用程序中执行 FFT。该库内部包含了多种实现，并且有一个 benchmark工具用来比较每种实现的性能。