4. 数字调制¶

在本章中，我们将学习使用数字调制（Digital Modulation）和无线符号（Wireless Symbols）去 实际传输数据 ！我们将使用 ASK、PSK、QAM、FSK 等调制方案去设计一些能传达 “信息” 的无线信号，例如 1 和 0。我们还将讨论 IQ 图和星座图（Constellation），并以一个 Python 示例收尾本章。

调制的哲学在于 “将尽可能多的传输数据塞进尽可能窄的频谱资源里”。从技术角度定义，即我们希望以 bit/s/Hz 为单位的频谱效率尽可能大。回忆一下傅里叶变换的相关性质：无线信号传输 1 和 0 的速度越快，其频谱宽度（带宽）就越大。除了讨论如何加速传输速度外，我们还将讨论一些其他技术。选择调制方法往往充满了权衡和妥协，但是在其中也存在着很多想象和创造空间。

符号¶

新术语警告！发射机所传输的信号将由 “符号（Symbol）” 组成。每个符号将携带一些比特，在通信中我们可能会连续发送成千上万个符号。

举个例子，假设我们有一根线缆，其中用高电平和低电平分别代表 1 和 0 进行传输，那么这里一个符号就是一个 1 或 0：

在上面的示例中，一个符号携带一个比特的信息。你可能想问，如何在每个符号中传输多于一个比特的信息呢？让我们来研究一下以太网信号，其在一个名为 IEEE 802.3 1000BASE-T 的 IEEE 标准中被定义。在以太网中，一个符号具有 4 种可能的幅度（因而携带 2 比特的信息），并且每个符号的传输时间是 8 纳秒。

IEEE 802.3 1000BASE-T 标准下的以太网信号的电平变化，展示了 4 级幅度调制（ASK）。

请思考以下问题：

上图例子中，每一秒能传输多少比特的信息？
如果想要达到 1 Gbps 的信息传输速率，需要多少对这样的数据流？
如果采用 16 级幅度调制，每个符号能携带多少比特的信息？
如果一个符号的传输时长还是 8 纳秒，但是使用 16 级幅度调制，那么每秒能传输多少比特的信息？

Answers

250 Mbps - (1/8e-9)*2
4 （这也是千兆以太网线缆的真实配置）
每个符号 4 比特 - log_2^(16)
0.5 Gbps - (1/8e-9)*4

无线符号¶

提问：为何我们不能在无线通信系统中直接传输以太网信号？原因有很多，但是最主要的是如下两个：

低频信号需要巨大的天线，而上文的信号包含了从 DC（0 Hz）开始的频率。我们无法传输 DC 信号。
方波信号在频域中会占用大量带宽—请回忆频率域章节中的内容：时域中信号变化越锐利（比如方波的直角），频域中宽度就越大。

我们对无线信号的处理始于 “载波（Carrier）”，也即一个正弦波。例如某些 FM 广播的载波是频率为 101.1 MHz 或 100.3 MHz 的正弦波。虽然 FM 广播使用的是模拟调制（Analog Modulation），但是它的核心理念和数字调制是一样的。

如何调制载波？这个问题等价于 “一个正弦波有哪些属性可以被改变” ？

幅度（Amplitude）
相位（Phase）
频率（Frequency）

通过改变上述的一种或多种属性，我们可以将数据调制到载波上。

幅移键控（ASK）¶

幅移键控（Amplitude Shift Keying，ASK）是我们将要讨论的第一种数字调制方案，因为幅度是三个正弦波属性中最容易可视化的。我们可以直观地改变载波的幅度，以下是二进制 ASK 即 2-ASK 的示例：

注意，图中无线信号的纵坐标平均值为零。在讨论调制时，人们往往喜欢这样展现数据和绘图。

我们可以使用多于两个幅度级别，从而让每个符号携带更多比特。以下是 4-ASK 的示例。在这种情况下，每个符号携带 2 比特的信息。

提问：上面的信号片段中有多少个符号？总共携带了多少比特的信息？

Answers

20 个符号，总共携带了 40 比特的信息。

那么，我们如何通过写代码的方式创造出这些数字信号呢？答案不难，我们只需要创建一个向量使得一个符号包含 N 个采样点，然后将该向量乘以一个正弦波。这样就将信号调制到了一个载波上（这个正弦波就是载波）。以下示例展示了 2-ASK，其中每个符号包含 10 个采样点。

2-ASK 的时域示例图，其中每个符号包含 10 个采样点（即 10 sps）。

上图中，顶图展示的是由红色点表示的离散采样点（即我们生成的数字信号），底图展示的是调制后的真正能在空中发出的信号。在真实的通信系统中，载波的频率通常远远高于符号变化的频率：在这个例子中，每个符号包含载波（正弦波）的三个周期，但在实际中可能包含数千个周期，具体取决于载波频率有多高。

相移键控（PSK）¶

现在，让我们考虑以与调制幅度类似的方式去调制相位，即相移键控（Phase Shift Keying，PSK）。最简单的形式是二进制相移键控，即 BPSK，其仅包含对载波的两种相位改变：

无相位改变（0 度）
相位反转（180 度）

BPSK 的示例（请关注载波的相位变化）:

正如你所见，BPSK 从时域角度并不容易看清：

所以我们倾向于使用复平面上的星座图来可视化它。

IQ 图/星座图¶

你应该在 IQ 采样章节中已经见过 IQ 图了，但是现在我们将以一种新的有趣方式使用它。对于给定的符号，我们可以在 IQ 图上展示它的幅度和相位。对于 BPSK 示例，符号仅有 0 和 180 度两种相位，让我们在 IQ 图上绘制这两个点。我们将假设幅度为 1，但是实际上幅度并不重要：在 BPSK 中，更高的值仅仅意味着更高功率的信号而与符号的内容无关。

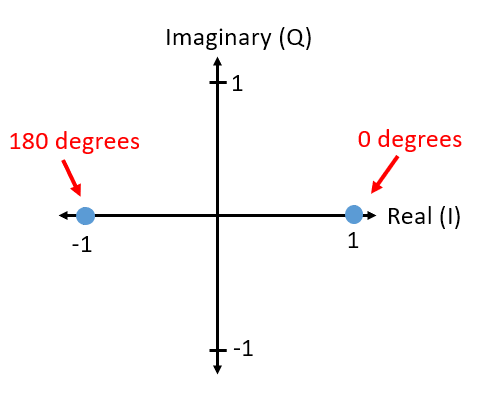
上面的 IQ 图展示了我们将要发送的符号或者符号的集合。它并不展示载波，所以你可以认为它是基带（Baseband）符号。当我们在图中展示了给定调制方案的所有可能符号时，我们称之为 “星座图（Constellation）”。许多调制方案都可以由星座图来定义。

通过使用 IQ 采样（就像我们在上一章中学到的那样），然后检查这些采样点在 IQ 图中的位置，我们可以实现对 BPSK 信号的解码。然而，在真实的通信系统中，信号经由无线信道会经历一些随机延迟，因此会有随机相位旋转。这种随机相位旋转可以通过我们后面将学到的各种方法来逆转。以下是 BPSK 信号在接收端可能呈现的几种不同 IQ 图的示例（在没有噪声的情况下）：

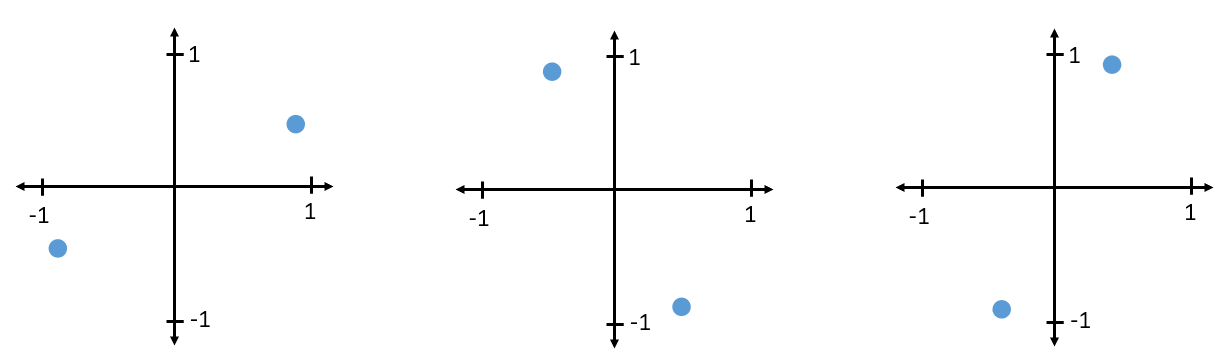
回到 PSK，如果我们想要四种不同的相位级别，即 0、90、180 和 270 度，那么它将在 IQ 图上表示如下，形成我们称为 “正交相移键控（Quadrature Phase Shift Keying，QPSK）” 的调制方案：

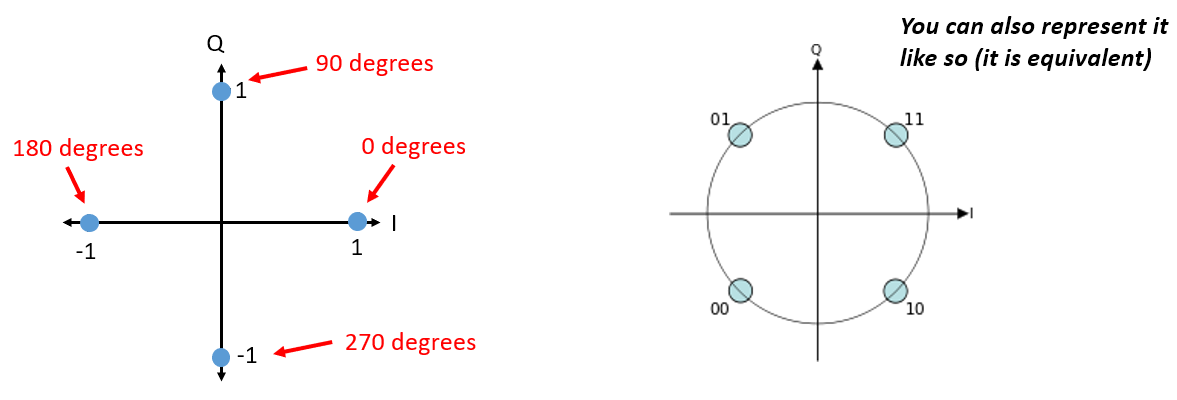
对于不同的 PSK 调制方案，我们总是会设计 N 种均分 360 度的相位级别。我们通常会把它们画在单位圆上，以强调所有点的幅度都是相同的：

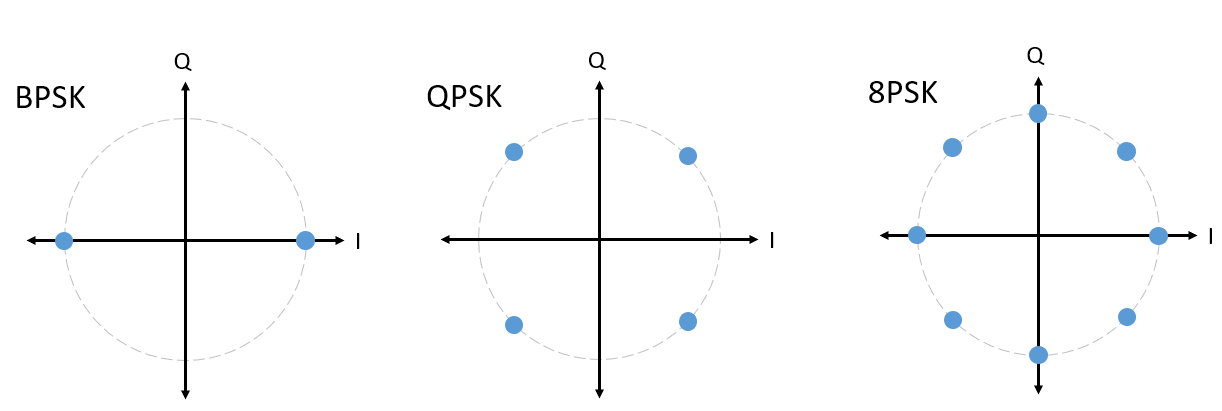
提问：下图展示的 PSK 方案有什么问题？它是一个有效的 PSK 调制方案吗？

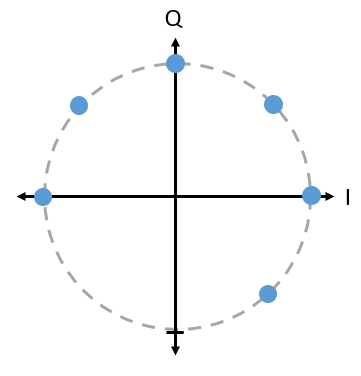
Answer

这个 6-PSK 方案没有错误，你甚至可以在真实的通信系统中使用它。但是，由于符号没有均匀分布在单位圆上，图中的方案并不是最有效的 6-PSK 方案。在后文我们讨论噪音对符号的影响时，你能更透彻地理解其原因。简而言之，一个最有效的方案将在符号之间留出尽可能多的空间，以尽可能避免噪声让接收机错误地解码符号，比如将 0 当作 1。

现在，让我们暂时回到 ASK 方案。我们可以像展示 PSK 一样在 IQ 图上展示 ASK。以下是双极（Bipolar） 2-ASK、4-ASK 和 8-ASK，以及单极（Unipolar） 2-ASK 和 4-ASK 的 IQ 图。

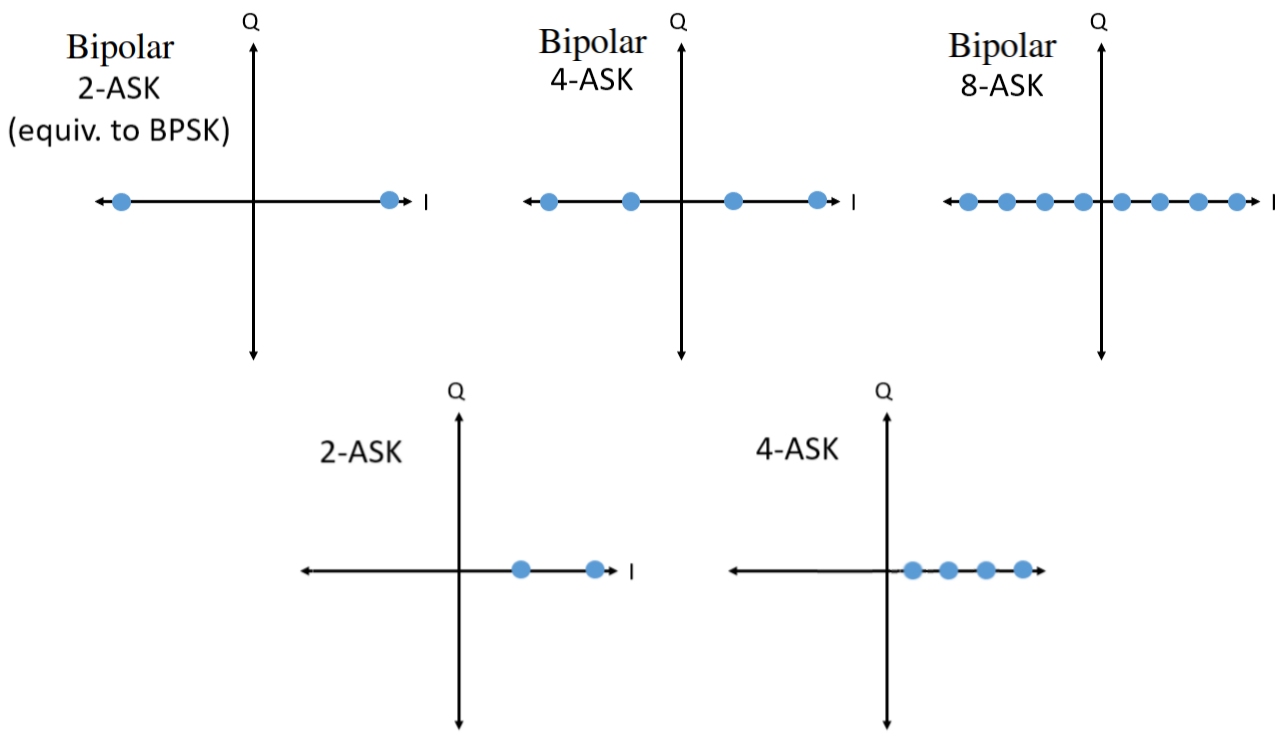
你可能注意到了，双极 2-ASK 和 BPSK 没有区别，因为 180 度的相位变化等同于将正弦波乘以 -1。但是对于双极 2-ASK/BPSK 而言，人们常常统一称之为 BPSK，因为 PSK 相比 ASK 更常用。

正交幅度调制（QAM）¶

我们可以将 ASK 和 PSK 结合吗？可以，我们称之为正交幅度调制（Quadrature Amplitude Modulation，QAM）。 QAM 的星座图通常看起来像这样：

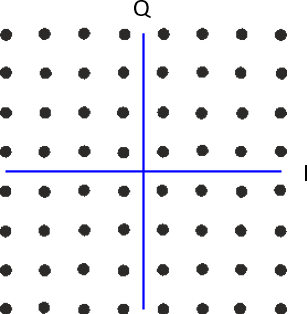
这里还有更多的 QAM 星座图示例：

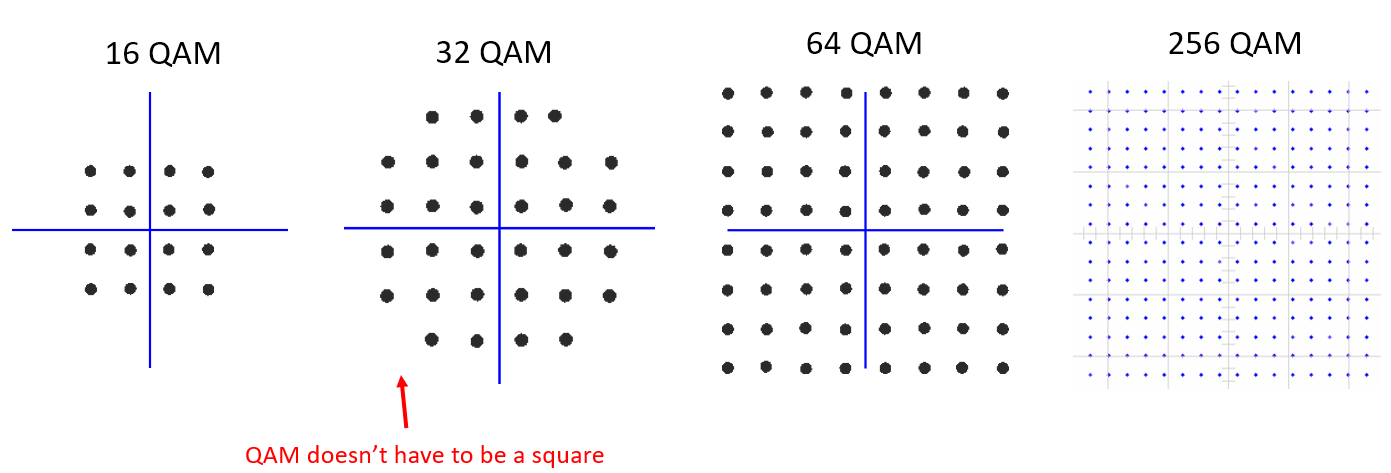
在设计 QAM 时，理论上我们可以把符号放在 IQ 图上的任何位置，因为 QAM 会同时对相位和幅度进行调制。展示一个 QAM 方案 “参数” 的最好方式是直接画出它的星座图。或者，你也可以列出每个符号的 I 和 Q 值，如下面展示的 QPSK（译者注：QPSK 也是一种 QAM 哦！）：

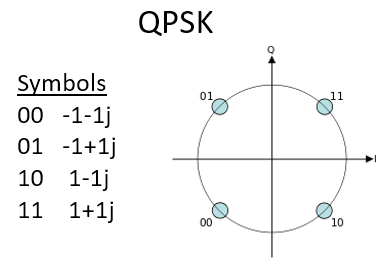
对于大部分调制方案而言，除了 ASK 和 BPSK，我们都是很难在时域中 “看清” 它们的。为了证明这一点，以下是一种 QAM 在时域中的示例。你能区分出每个符号的相位吗？这很困难。

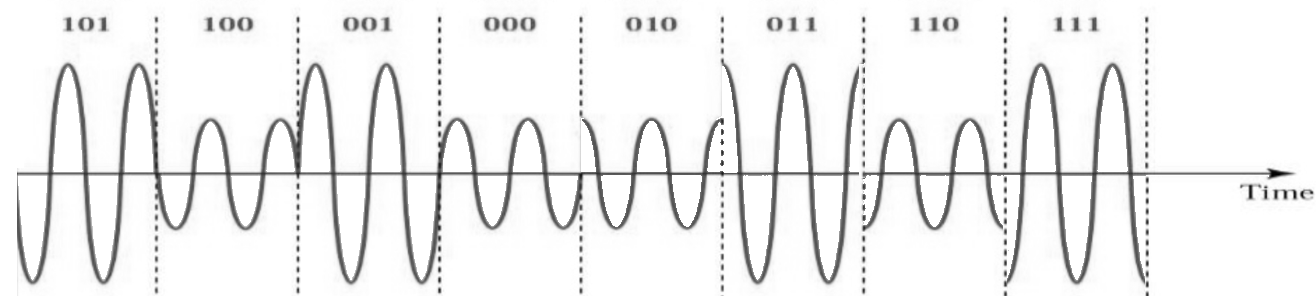
由于从时域上很难看清，我们更倾向于使用 IQ 图来可视化。但是偶尔当存在特定的数据包结构或者符号序列需要阐明时，我们也会展示时域信号。

频移键控（FSK）¶

最后要讨论的就是频移键控（Frequency Shift Keying，FSK）了。 FSK 是相当容易理解的—我们在 N 个频率之间切换，每个频率对应一个可能的符号。因为我们是在调制载波，所以实际上是在载波频率上加减这 N 种频率。例如，我们可能在 1.2 GHz 的载波频率上切换以下四个频率：

1.2005 GHz
1.2010 GHz
1.1995 GHz
1.1990 GHz

上面这个例子就是一个 4-FSK，每个符号携带 2 比特的信息。在频域中，一个 4-FSK 信号可能看起来像这样：

在设计 FSK 时，你一定会遇到一个关键问题：相邻频率之间的频谱间距应该是多少？我们通常把这个间距用 $\Delta f$ 表示（单位是 Hz）。我们希望在频域中避免频率重叠，这样接收机才能根据不同的频率辨别符号，所以 $\Delta f$ 必须足够大。而每种频率的宽度则取决于我们的符号速率：每秒需要传输的符号越多，每个符号的持续时间越短，其频率宽度就越宽（回忆一下时间和频率之间的反比关系）。那么相应的， $\Delta f$ 就需要越大，以避免不同频率之间出现重叠。我们暂时不会在本教材中深入讨论 FSK 的设计细节。

IQ 图无法展示不同的频率，它们展示的是幅度和相位。虽然在时域中展示 FSK 是可能的，但是超过 2 个频率仍然会使符号之间的区分变得困难：

另外，需要注意的是，FM 广播使用的是频率调制（Frequency Modulation，FM），这种调制方法可以当作是 FSK 的模拟信号版本。不同于 FSK 中不同符号所使用的离散频率，FM 广播使用连续的音频信号来调制载波频率。下面是调频（FM）和调幅（AM）的示例，顶部的 “信号” 是需要调制到载波上的音频信号。

在本教材中，我们主要关注数字信号调制方法。

差分编码¶

在许多基于 PSK 和 QAM 的无线以及有线通信协议中，你可能会遇到一种称为差分编码（Differential Coding）的步骤，它在调制之前以及解调之后发生。我们以 BPSK 信号的接收举例：正如我们之前提到的，信号通过无线信道会经历一些随机延迟，这会导致星座图中的符号随机旋转。当接收机与之同步，并将 BPSK 对齐到 “I”（实数）轴时，因为星座图是对称的，它无法知道是否相位旋转了 180 度。一种解决方案是在信息中额外插入接收机预先知道取值的符号，这种符号称为导频符号（Pilot Symbols）。对于 BPSK 而言，接收机可以使用这些已知符号来确定哪个簇是 1 或 0。导频符号必须以某种与无线信道变化的速度有关的周期发送，此外，额外插入导频符号会降低有效数据传输速率。此时，差分编码方案闪亮登场，可以让我们避免在传输信号中混入大量的导频符号。

与 BPSK 一起使用的差分编码方案是最简单的。在差分 BPSK 调制中，一个符号包含 1 比特的信息。与仅仅传输二进制比特时的 1 为 1， 0 为 -1 不同，差分 BPSK 在输入比特与前一个比特的编码（而不是前一个输入比特本身）相同时传输 0，反之传输 1。由此，我们仍然传输着相同数量的比特（除了在开始输出序列时需要额外插入的一个参考比特），但不必再担心 180 度相位模糊。这种编码方案可以用以下公式描述，其中 $x$ 是输入比特， $y$ 是经过了差分 BPSK 调制后的输出比特：

$y_i = y_{i-1} \oplus x_i$

由于输出依赖于上一步的输出，所以在传输开始前，我们需要先引入一个参考比特，它可以是 1 或 0，它会作为第一个比特被传输。

下面也准备了差分编码的流程图供视觉学习者们参考，其中延迟块的操作为延迟 1 个单位：

接下来，我们讨论一个具体的差分 BPSK 编码示例。假设发射机要传输 10 个比特： [1, 1, 0, 0, 1, 1, 1, 1, 1, 0]，我们可以任意选择 0 或 1 作为起始参考比特（具体选哪一个并不重要），在下面的示例中，我们以 1 作为起始参考：

Input:     1 1 0 0 1 1 1 1 1 0
Output:  1

接下来，你只需要将输入位与先前的输出位进行比较，并应用上面表中显示的 XOR 操作来构建输出。因为 1 和 1 匹配，所以下一个输出位是 0：

Input:     1 1 0 0 1 1 1 1 1 0
Output:  1 0

重复这个过程，最后你将得到：

Input:     1 1 0 0 1 1 1 1 1 0
Output:  1 0 1 1 1 0 1 0 1 0 0

应用差分编码后，我们最终传输的符号/比特为 [1, 0, 1, 1, 1, 0, 1, 0, 1, 0, 0]。

解码过程发生在接收机处，将接收到的比特与先前接收到的比特进行比较，用公式表达即：

$x_i = y_i \oplus y_{i-1}$

如果接收端收到了 BPSK 差分编码后的符号 [1, 0, 1, 1, 1, 0, 1, 0, 1, 0, 0]，那么在解码时，你只需要从左到右检查每两个符号是否匹配：如果不匹配，那么这一位原始信号的比特就是 1 反之则为 0。重复这个过程，你将得到我们希望传输的原始序列 [1, 1, 0, 0, 1, 1, 1, 1, 1, 0]。略加思考，你会发现添加在头部的参考比特是 1 或 0 都不会影响最终结果。

作为总结，编码和解码过程如下图所示：

差分编码的一个主要缺点是，一个错误比特可能会导致两个比特错误。对于BPSK，一种改进的差分方案是定期添加导频符号，这些符号有助于对抗信道引起的多径效应。然而，导频符号也有其弱点，特别是在信道快速变化的情况下。如果信道发生快速变化，发射端需要频繁插入导频符号以适应快速变化的信道条件。比如当发射机/接收机移动时，这种变化的时间尺度可能仅是几十个或几百个符号。为了降低接收机的复杂性，一些无线协议（如 rds-chapter 章节中研究的 RDS）选择使用差分编码，即使差分编码存在一些缺点。

最后值得强调的是，上述差分编码示例是特定于 BPSK 的。差分编码作用于符号层面，因此若想将其应用于 QPSK，你需要一次处理若干对比特，更高阶 QAM 方案则以此类推。差分 QPSK 通常被称为 DQPSK。

Python 示例¶

我们将展示一个生成 QPSK 基带信号并绘制其星座图的 Python 示例。

尽管我们可以直接生成复数符号，但先让我们从 QPSK 有围绕单位圆的 90 度间隔四个符号的知识开始。我们将使用 45、135、225 和 315 度作为我们的符号点。首先，我们会生成 0 到 3 之间的随机数，并进行数学运算以获得我们想要的角度，然后转换为弧度。

import numpy as np
import matplotlib.pyplot as plt

num_symbols = 1000

x_int = np.random.randint(0, 4, num_symbols) # 0 to 3
x_degrees = x_int*360/4.0 + 45 # 45, 135, 225, 315 度
x_radians = x_degrees*np.pi/180.0 # sin() 和 cos() 以弧度为输入
x_symbols = np.cos(x_radians) + 1j*np.sin(x_radians) # 生成 QPSK 复数符号
plt.plot(np.real(x_symbols), np.imag(x_symbols), '.')
plt.grid(True)
plt.show()

从上图可以观察到我们生成的信号完全重合了。这是因为没有引入噪音，所有信号点的取值都等于理论值因而相同。

n = (np.random.randn(num_symbols) + 1j*np.random.randn(num_symbols))/np.sqrt(2) # 具备单位功率噪音的 AWGN
noise_power = 0.01
r = x_symbols + n * np.sqrt(noise_power)
plt.plot(np.real(r), np.imag(r), '.')
plt.grid(True)
plt.show()

请观察并思考加性白高斯噪声（AWGN）如何在星座中的每个点周围产生均匀分布。如果噪声太大，那么符号将开始越过边界（四个象限），此时接收机将开始把原始符号解码为不正确的符号。你可以尝试增加 noise_power 直到这种情况发生。

有些人可能对相位噪音感兴趣，这些噪音往往由于本地振荡器（LO）内的相位抖动而产生，可以将 r 替换为：

phase_noise = np.random.randn(len(x_symbols)) * 0.1 # 在这里可以调整相位噪音的强度
r = x_symbols * np.exp(1j*phase_noise)

你甚至可以将相位噪声与 AWGN 结合起来，以获得逼近真实信道的完整的体验：

本章的内容至此就结束了。如果想看 QPSK 信号在时域中的样子，你还需要为每个符号生成多个采样点（在这个示例代码中我们只为每个符号生成了 1 个采样点）。你将在本教材后续的脉冲整形（Pulse Shaping）章节中学到为什么需要为每个符号生成多个采样点。 pulse-shaping-chapter 章节中的 Python 示例将继续我们停止在这里的工作。

拓展阅读¶

https://en.wikipedia.org/wiki/Differential_coding