6. 噪声与分贝（dB）¶

本章将详细讨论噪声的相关主题，特别是噪声在无线通信系统中的建模和处理方式。涉及的概念包括加性高斯白噪声（AWGN）、复数噪声、信噪比（SNR）、信干噪比（SINR）。同时，我们还会介绍在无线通信和软件定义无线电（SDR）中广泛使用的分贝（dB）单位。

高斯噪声¶

噪音的本质是指那些不需要的信号波动，它们会干扰我们所追求的信号，它看起来可能是这样：

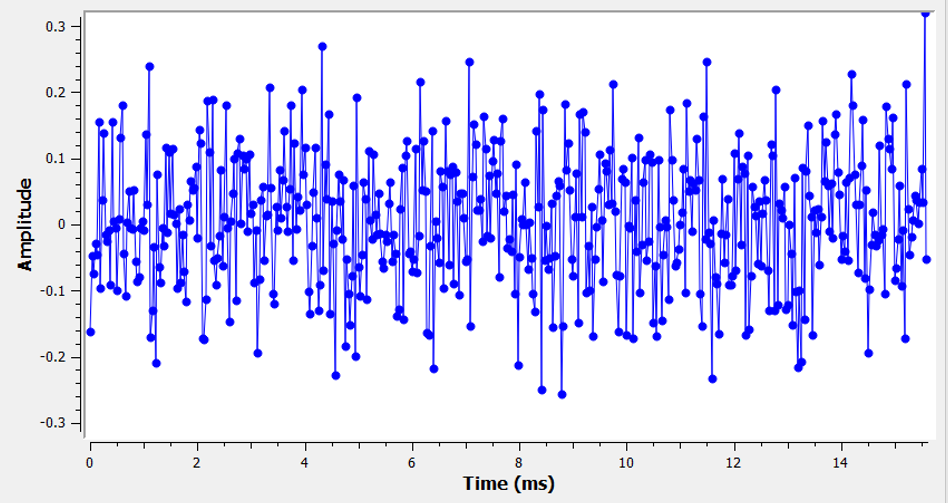
在时间域中，图上的纵坐标的平均值为零。如果平均值不为零，我们可以减去平均值来得到一个偏置，从而使剩余部分的平均值为零。此外，需要注意的是图中的各个点 并不是 均匀随机分布的。大多数点接近零，而远离零的点较少。

这种类型的噪声被称为 “高斯噪声”（Gaussian Noise），它是许多自然噪声的良好模型。例如，在接收机射频组件中，硅原子的热振动可以用高斯噪声来描述。根据 中心极限定理，多个随机过程的加和结果往往近似服从高斯分布，即便某些过程可能采用其他分布。对于大量随机事件也是同理，其结果的分布趋近于高斯分布，即便各个事件本身的分布并不是高斯分布。

Central limit theorem visualized as the sum of many random processes leading to a normal distribution (a.k.a. gaussian distribution)

高斯分布也被称为 “正态” 分布（回想一下钟形曲线）。

高斯分布有两个参数：均值和方差。上文已经提到均值可以视为零，因为哪怕实际上不为零，你也可以将其视为恒定偏差并减去。方差则决定了噪声的 “强度”，因为方差越大，越有可能出现较大的数。因此，我们可以说高斯噪声的强度是由方差定义的。

方差等于标准差的平方（ $\sigma^2$ ）。

分贝（dB）¶

我们将简要介绍一下分贝（dB）。如果你已经熟悉这个概念，可以跳过这一部分。

当我们需要同时处理小数和大数，或者只是一组非常大的数时，使用分贝是极其有用的。想象一下，在示例 1 和示例 2 中使用相应规模的数字是多么繁琐：

示例1：信号 1 的接收功率为 2 瓦特，底噪为 0.0000002 瓦特。

示例2：垃圾处理器的噪声是安静的农村地区环境噪声的 100,000 倍，链锯的声音甚至比垃圾处理器还大 10,000 倍（以声波功率为单位）。

如果我们不使用 dB，而是用 “线性” 方式来表示这些值，我们需要很大的数值范围来表示示例 1 和示例 2 中的值。假设我们要绘制信号 1 的接收功率随时间变化的图像，并将 y 轴刻度选为 0 到 3 瓦特，那么噪声的值将远低于可见范围。因此，为了在同一张图中同时表示差异如此悬殊的两种值，我们需要使用对数坐标。

为了进一步说明信号处理中的规模问题造成的影响，下面绘制了两张瀑布图，它们包含了相同的三种信号，且使用了相同的颜色映射（蓝色为最低值，黄色为最高值）。唯一的区别是，左图使用的是线性坐标，右图使用的是对数坐标（dB）。你会发现，左图对信号的表现能力差很多。

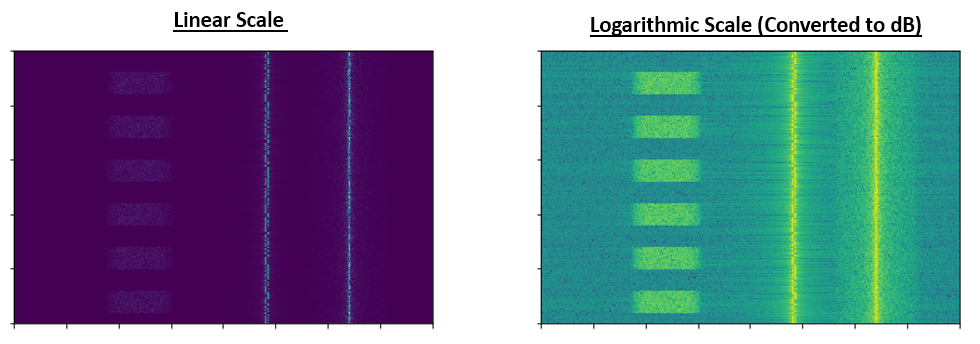
Depiction of why it's important to understand dB or decibels, showing a spectrogram using linear vs log scale

给定一个值 x，我们可以使用以下公式将 x 转换为 dB：

$x_{dB} = 10 \log_{10} x$

Python 代码:

x_db = 10.0 * np.log10(x)

你可能会发现在其他领域中，表达式中的 10 * 可能需要改为 20 * 。当处理代表功率的量时，常用系数 10，但当处理代表非功率量如电压或电流时，更适合使用系数 20。在DSP领域，我们通常处理代表功率的量。实际上，在本书中我们没有使用过 20，而始终使用 10。

我们使用以下方法将 dB 转换回线性数值（普通数值）：

$x = 10^{x_{dB}/10}$

Python 代码:

x = 10.0 ** (x_db / 10.0)

为了理解 dB，请不要陷在数学公式里，而是抓住它的核心作用。在 DSP 中，我们常常需要同时处理非常大和非常小的数，例如信号强度与噪声强度的比较。 dB 的对数刻度使我们能够在表达数字或绘制图形时拥有更大的动态范围。它还提供了一些便利，比如在通常需要乘法的情况下，我们可以使用加法（正如我们将在链路预算章节中看到的那样）。

这里有人们初次接触 dB 时常犯的一些错误：

使用自然对数而不是以 10 为底的对数，这个错误很容易犯，因为很多编程语言中，log() 函数实际上是自然对数。
在表达数字或标记坐标轴时忘记包含 dB。如果我们使用的是 dB，我们需要在某处标识它。
当你使用 dB 时，你需要加减值，而不是乘除，例如：

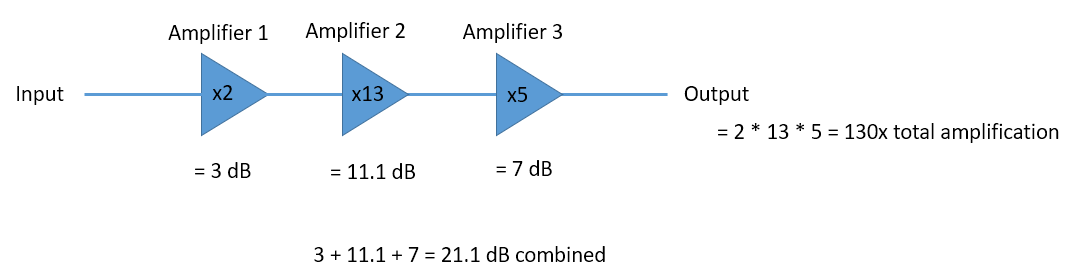
还需要记住，dB 并不是严格意义上的 “单位”。一个 dB 的数值本身是无单位的，就像说某物体是 “2 倍大” 一样，在上下文告诉你单位之前，它本身是没有单位的。 dB 是一个相对的概念。在音频处理中，当人们说 dB 时，他们实际上是指 dBA 这个单位（其中 A 是某物理单位）。在无线电领域，我们通常使用瓦特来表示实际功率。因此，你可能会看到 dBW 这个单位，它其实表示相对于 1 W 的大小。你也会见到 dBmW（简写为 dBm），它表示相对于 1 mW 的大小。例如，人们可能会说 “我们的发射机功率设置为 3 dBW”（其实就是 2 瓦）。有时候人们也会就说 xx dB，这时候表示相对大小，没有单位，比如 “我们接收到了相对于底噪 20 dB 的信号”。此外，0 dBm = -30 dBW，记住它对你也许会有帮助。

这里还有更多的对照，我建议你也一并记住：

线性	dB
1x	0 dB
2x	3 dB
10x	10 dB
0.5x	-3 dB
0.1x	-10 dB
100x	20 dB
1000x	30 dB
10000x	40 dB

最后，为了更直观地展示这些数字，以下是一些功率水平示例，以 dBm 为单位：

80 dBm	乡村地区调频广播（FM）电台的发射功率
62 dBm	业余无线电（HAM）发射机的最大发射功率
60 dBm	家用微博炉的功率
37 dBm	典型手持对讲机或无线电发射机的最大发射功率
27 dBm	典型的手机发射功率
15 dBm	典型的 WiFi 发射功率
10 dBm	蓝牙 4.x 最大传输功率
-10 dBm	WiFi 的最大接收功率
-70 dBm	业余无线电（HAM）可能的接收功率
-100 dBm	WiFi 的最小接收功率
-127 dBm	典型的 GPS 卫星信号接收功率

频域角度看噪声¶

在频率域章节中我们讨论了 “傅里叶变换对”（Fourier Pairs），即某个信号在时域及对应频域的样子。那么，高斯噪声在频域中是什么样子呢？下面的图显示了时域中的一些模拟噪声（图的上部）以及该噪声的功率谱密度（PSD）的图（图的下部）。这些图是从 GNU Radio 中截取的。

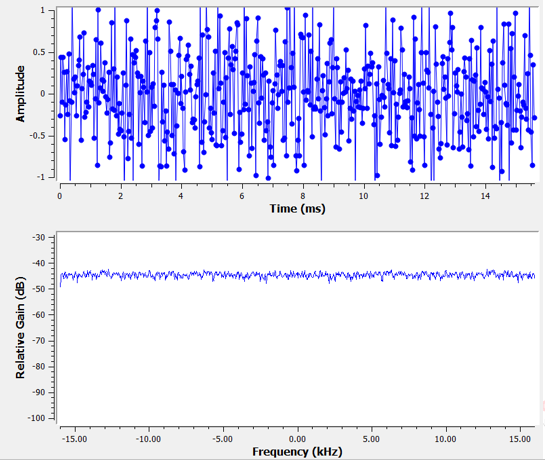
AWGN in the time domain is also Gaussian noise in the frequency domain, although it looks like a flat line when you take the magnitude and perform averaging

从下方的频谱图可以看到，所有频率上的功率谱密度都大致相同且相对平坦。这证明，高斯噪声在频域中也是呈高斯分布的。上面的两个图看起来还是有区别，一方面是因为频谱图显示的是 FFT 的幅度，所以只会有正数，另一方面是因为它使用对数刻度（dB）显示幅度。否则，它们两张图看起来会差不多。我们可以自行用 Python 在时域生成一些噪声，然后进行 FFT 来证明这一点。

import numpy as np
import matplotlib.pyplot as plt

N = 1024 # 选择样本数量用于模拟，可自定义
x = np.random.randn(N)
plt.plot(x, '.-')
plt.show()

X = np.fft.fftshift(np.fft.fft(x))
X = X[N//2:] # 只看正频率，// 表示取整除法
plt.plot(np.real(X), '.-')
plt.show()

请注意，默认情况下，randn() 生成的数据符合标准正态分布（均值为 0，方差为 1）。代码生成的两张图像看起来都会类似这样：

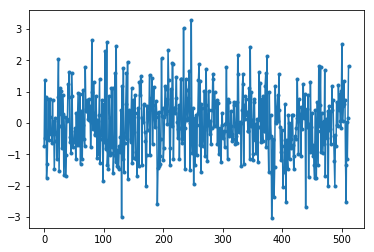
Example of white noise simulated in Python

只需对上面的 FFT 输出取对数并进行平均，你就可以复现上文来自 GNU Radio 的那张平坦的 PSD 图像。我们生成并进行 FFT 的信号是实信号（而不是复信号），任何实信号的 FFT 都会有相抵的负数和正数部分，所以我们只保存了 FFT 输出的正部分（第二部分）。你可能会问，为什么？难道不能生成复数噪声吗？诶，别急，马上见分晓。

复数噪声¶

“复高斯噪声” 指的是基于基带信号的高斯噪声，其特点是噪声功率在实部和虚部上均匀分布。同时，重要的是实部和虚部是相互独立的，知道其中一个并不能确定另一个的值。

生成复高斯噪声的 Python 代码是这样的：

n = np.random.randn() + 1j * np.random.randn()

诶，等等！上面的等式在功率上并不能产生与 np.random.randn() 相同 “大小” 的噪声（相同的功率）。我们可以使用以下方法计算零均值信号（或噪声）的平均功率：

power = np.var(x)

尽管 np.var() 计算的是方差，但是和平均功率是等价的。对于上文的信号 n 而言，算出来是 2。为了产生具有 “单位功率” 的复数噪声，即功率为 1（这样便于操作），我们必须使用：

n = (np.random.randn(N) + 1j*np.random.randn(N))/np.sqrt(2) # AWGN with unity power

要在时域中绘制复数噪声，与任何复数信号一样，我们需要两条线：

n = (np.random.randn(N) + 1j*np.random.randn(N))/np.sqrt(2)
plt.plot(np.real(n),'.-')
plt.plot(np.imag(n),'.-')
plt.legend(['real','imag'])
plt.show()

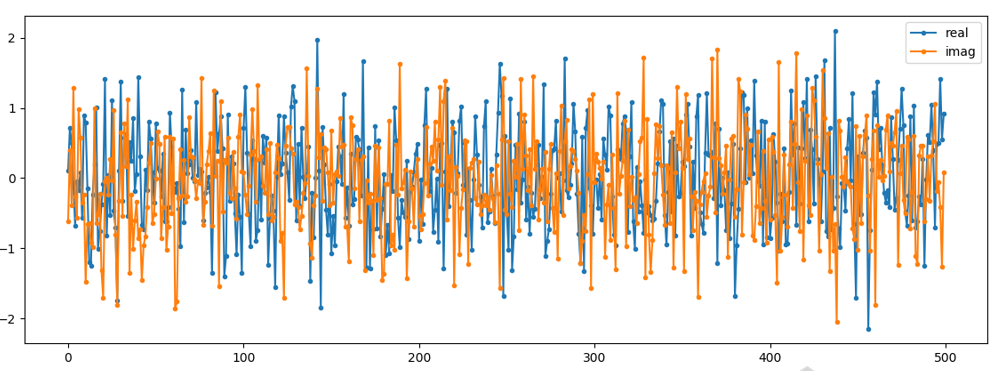
从上图可以看出来，实部和虚部是互相独立的。

复高斯噪声在 IQ 图上呈现什么样子？在 IQ 图上，实部表示在水平轴上，虚部表示在垂直轴上，它们都是独立的随机高斯分布：

plt.plot(np.real(n),np.imag(n),'.')
plt.grid(True, which='both')
plt.axis([-2, 2, -2, 2])
plt.show()

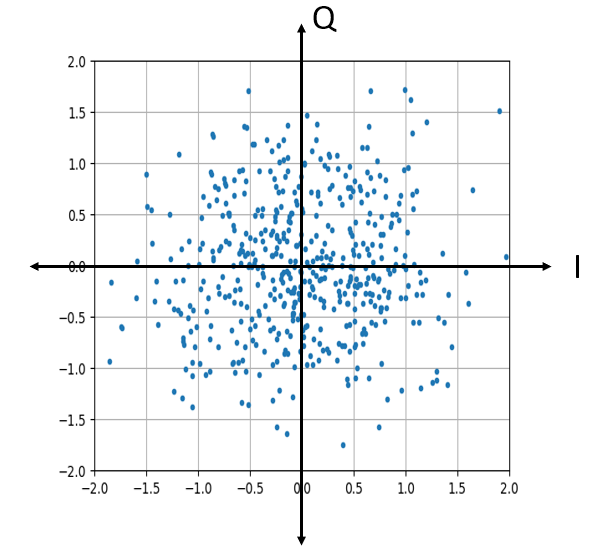
Complex noise on an IQ or constellation plot, simulated in Python

它的形状符合预期：一个以原点为中心的随机斑点分布，即 0+0j。为了增加趣味性，让我们尝试在一个 QPSK 信号中引入噪声，并观察 IQ 图的变化。

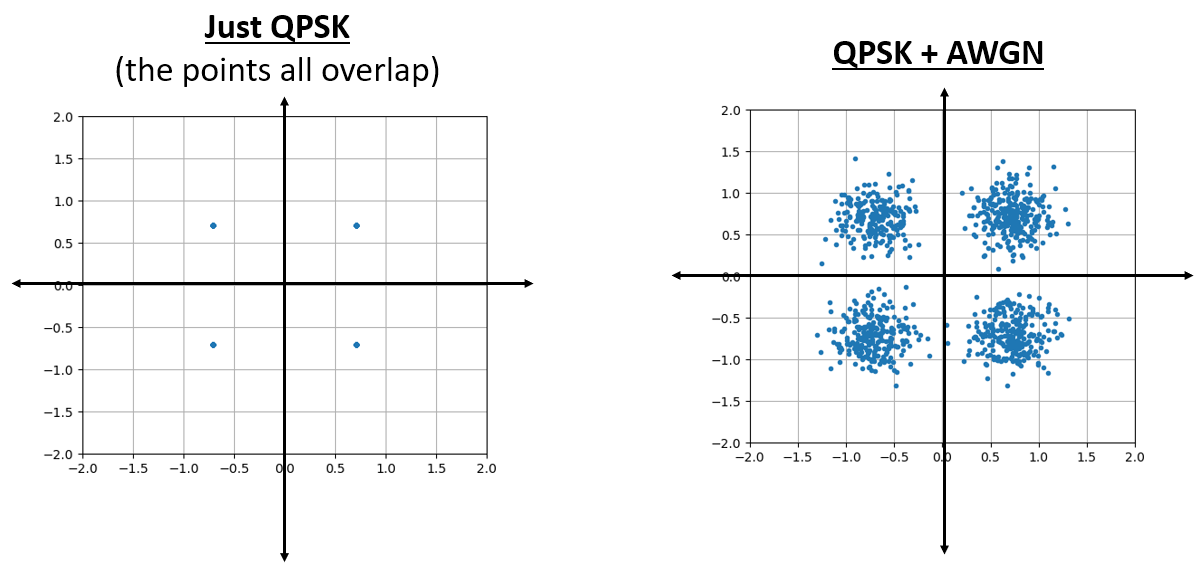
当噪声更强时，会发生什么呢？

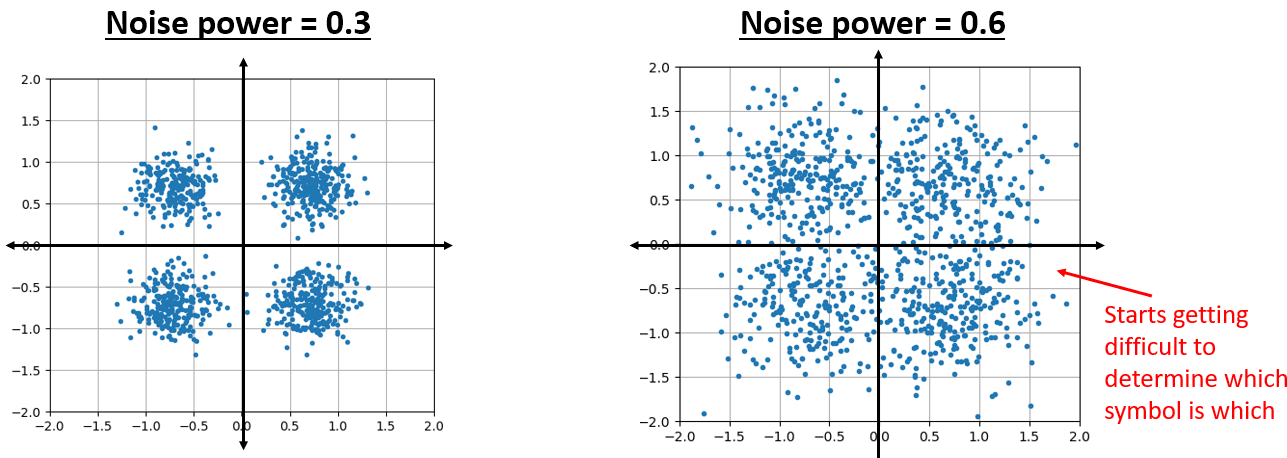
我们逐渐领悟到了无线数据传输的复杂性。在追求高效率的同时，我们也不得不面对噪声干扰所带来的问题。我们的目标是在每个数据符号中尽可能地传输更多的比特，但当噪声过高时，接收端很容易收到错误的比特。

AWGN¶

AWGN （Additive White Gaussian Noise，加性高斯白噪声）是 DSP 和 SDR 领域中经常能听到的缩写。 GN 指的是高斯噪声，我们之前已经讨论过了。Additive （加性）表示噪声是被添加到接收信号中的。 White （白）在频域上意味着我们整个观测频带上的频谱是平坦的，在实践中，它几乎总是白噪声，或者是近似白噪声。在本教材中，当处理通信链路和链路预算等问题时，我们将只考虑 AWGN 作为唯一形式的噪声。非 AWGN 噪声往往是一个专门的课题。

SNR 和 SINR¶

信噪比（Signal-to-Noise Ratio，缩写为 SNR）用于比较信号强度和噪声水平的差异，它是一个无单位的量（表示一个比例）。 SNR 在实践中通常以分贝（dB）表示。在无线通信的模拟实验中，我们经常编码使得信号满足单位功率（即等于 1）。这样，通过调整生成噪声的方差，我们可以产生 -10 dB 功率的噪声，从而创建 10 dB 的 SNR。

$\mathrm{SNR} = \frac{P_{signal}}{P_{noise}}$

$\mathrm{SNR_{dB}} = P_{signal\_dB} - P_{noise\_dB}$

当你看到 “SNR = 0 dB” 时，这意味着信号和噪声功率相等。正的信噪比意味着信号的功率比噪声大，而负的信噪比意味着噪声的功率比信号大。负信噪比下检测信号通常相当困难。

像我们之前提到的那样，信号的功率等于信号的方差。因此，我们可以将信噪比表示为信号方差与噪声方差的比率。

$\mathrm{SNR} = \frac{P_{signal}}{P_{noise}} = \frac{\sigma^2_{signal}}{\sigma^2_{noise}}$

信干噪比（Signal-to-Interference-plus-Noise Ratio，缩写为 SINR）与信噪比（SNR）基本相同，只是在分母上加入了干扰的部分。

$\mathrm{SINR} = \frac{P_{signal}}{P_{interference} + P_{noise}}$

干扰的构成取决于具体应用和场景，但通常是另一个信号干扰了我们感兴趣的信号（Signal Of Interest，缩写为 SOI），并且在频率上与 SOI 重叠、或者由于某种原因无法被滤除。

参考资料¶

关于AWGN，SNR和方差的更多资料可参考：