7. 滤波器¶
在本章中,我们将学习使用 Python 实现数字滤波器(Digital Filter)。 本章将涵盖不同类别的滤波器(FIR/IIR, 低通/高通/带通/带阻)的设计和实现。 最后,我们将介绍脉冲整形(Pulse Shaping),并在之后的 pulse-shaping-chapter 章节中进一步探讨。
滤波器基础知识¶
滤波器(Filters)在许多学科中被使用。 例如,图像处理领域大量使用以图像为输入输出的 2D 滤波器。 甚至每天早上冲咖啡时我们也会用到过滤器(译者注:英文里都是 Filter)来从液体中滤除固体。 在 DSP(数字信号处理)中,滤波器主要用于:
- 分离已合并的信号(例如,提取所需的信号)
- 接收信号后去除多余噪声
- 恢复以某种方式失真的信号(例如,音频均衡器就是一种滤波器)
当然,滤波器还有其他用途,但本章旨在介绍这一概念,而不是解释所有可能用到的过滤器。
也许你会认为我们只关心数字滤波器,毕竟本书探讨的是数字信号处理。 但实际上很多滤波器都是模拟(Analog)的,比如我们的 SDR 中位于接收端模数转换器(ADC)之前的那些滤波器。 下图并列显示了模拟滤波器的电路原理图和数字滤波算法的流程图。
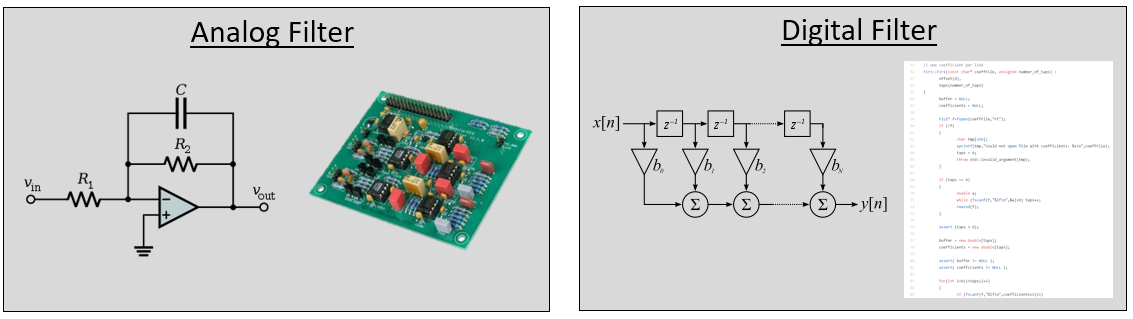
在数字信号处理中,输入和输出都是信号,每个滤波器都有一个输入信号和一个输出信号:

所以,一个滤波器不能输入两个不同的信号,除非先将这两个信号相加或进行其他操作。 同样,输出始终是一个信号,即一维数组。
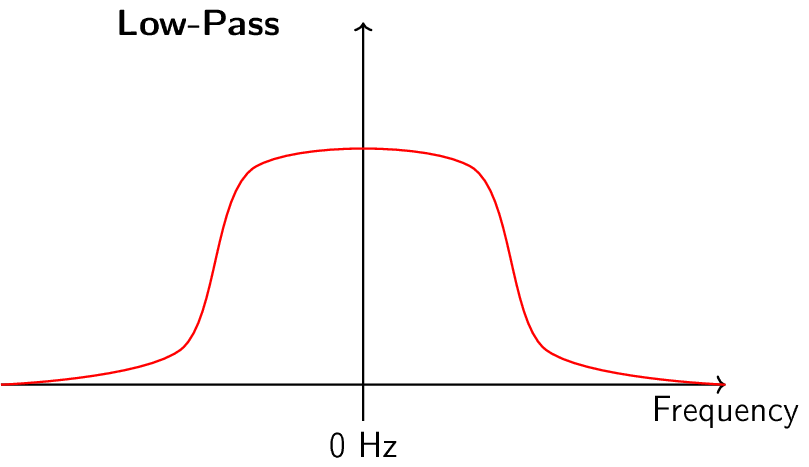
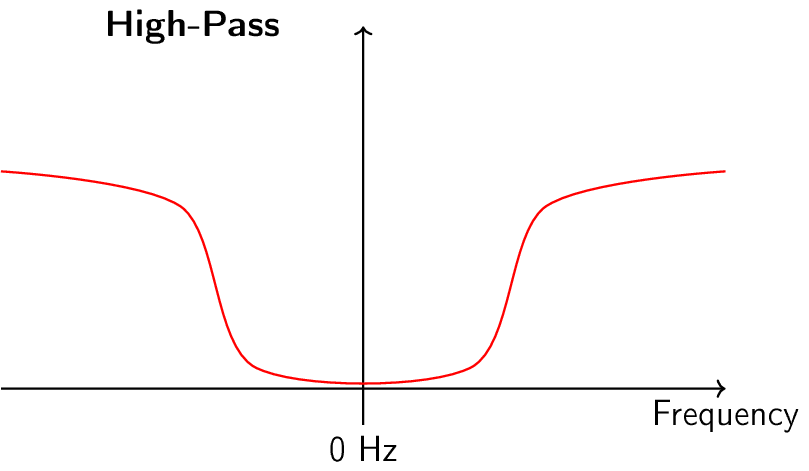
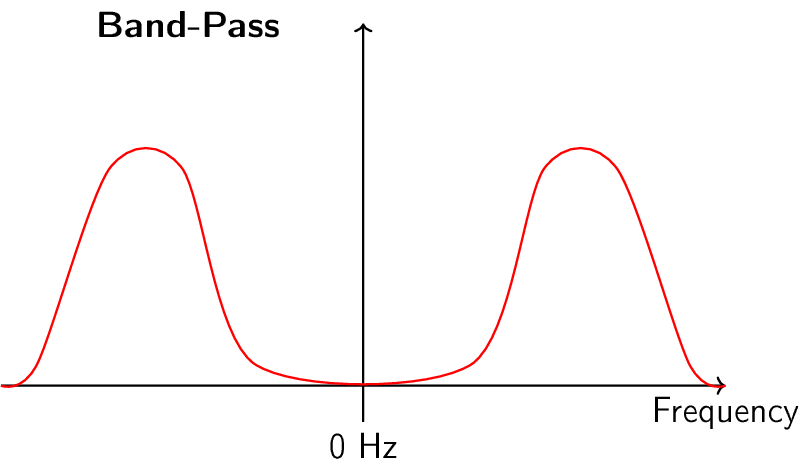
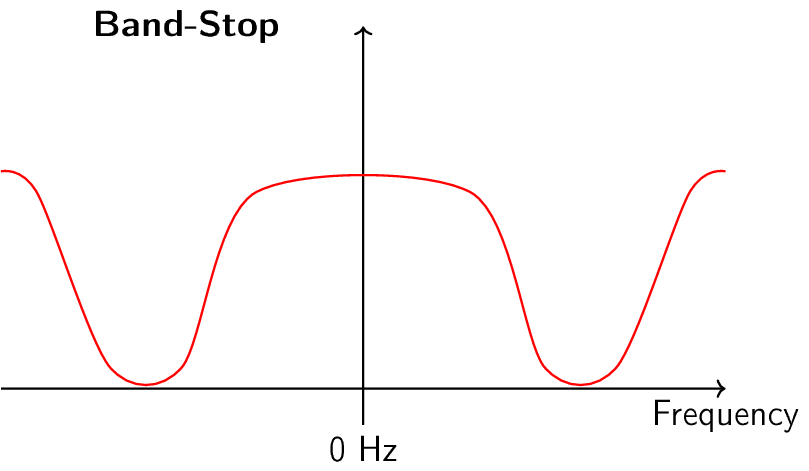
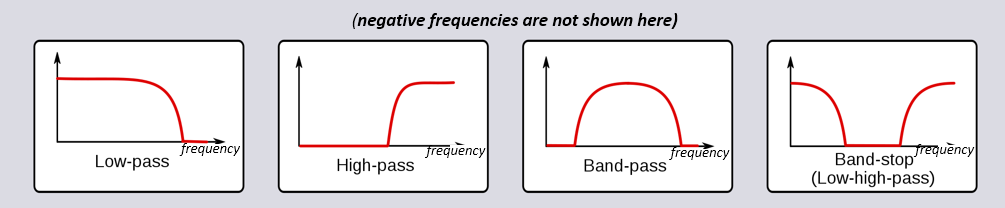
滤波器有四种基本类型:低通、高通、带通和带阻。每种类型的滤波器都会改变信号,使其集中在不同的频率范围内。 下面的图展示了每种类型的滤波器会怎样滤除信号中的频率,首先展示的是对正频率区间的处理(这更容易理解),然后是对负频率区间的处理。
|
|
|
|
每个滤波器都允许在信号中保留某些频率,同时阻断其他频率。 滤波器允许通过的频率范围称为 “通带”,而 “阻带” 指的是被阻断的频率范围。 就低通滤波器而言,它让信号的低频部分通过,而阻断高频的部分,因此 0 Hz 始终在通带内。而对于高通和带通滤波器,0 Hz 始终处于阻带之内。
请不要将这些滤波类型与滤波器的算法实现(如 IIR 与 FIR)混淆。最常见的滤波器类型是低通滤波器(Low-Pass Filter, LPF),因为我们通常以基带表示信号。 LPF 允许我们滤除信号 “周围” 的其它东西,包括多余的噪声和其他信号。
滤波器的表示¶
在使用中,大部分滤波器都是 FIR(Finite Impulse Response,有限脉冲响应)类型的,我们可以用一个浮点数数组来表示滤波器本身。 对于在频率域中对称的滤波器,这些浮点数将是实数(而不是复数),通常有奇数个。 我们称这个浮点数数组为 “滤波器抽头(Filter Taps)”。 我们通常使用 \(h\) 作为滤波器抽头的符号。以下是一组定义某个滤波器的滤波器抽头的例子:
h = [ 9.92977939e-04 1.08410297e-03 8.51595307e-04 1.64604862e-04
-1.01714338e-03 -2.46268845e-03 -3.58236429e-03 -3.55412543e-03
-1.68583512e-03 2.10562324e-03 6.93100252e-03 1.09302641e-02
1.17766532e-02 7.60955496e-03 -1.90555639e-03 -1.48306750e-02
-2.69313236e-02 -3.25659606e-02 -2.63400086e-02 -5.04184562e-03
3.08099470e-02 7.64264738e-02 1.23536693e-01 1.62377258e-01
1.84320776e-01 1.84320776e-01 1.62377258e-01 1.23536693e-01
7.64264738e-02 3.08099470e-02 -5.04184562e-03 -2.63400086e-02
-3.25659606e-02 -2.69313236e-02 -1.48306750e-02 -1.90555639e-03
7.60955496e-03 1.17766532e-02 1.09302641e-02 6.93100252e-03
2.10562324e-03 -1.68583512e-03 -3.55412543e-03 -3.58236429e-03
-2.46268845e-03 -1.01714338e-03 1.64604862e-04 8.51595307e-04
1.08410297e-03 9.92977939e-04]
使用案例¶
为了了解滤波器是如何使用的,让我们看一个例子,假设我们将我们的 SDR 调谐到一个现有信号的频率,并且我们想将其与其他信号隔离。 请记住,SDR 捕获的样本是在基带的,这意味着信号将以 0 Hz 为中心显示。 以下是可能接收到的信号:
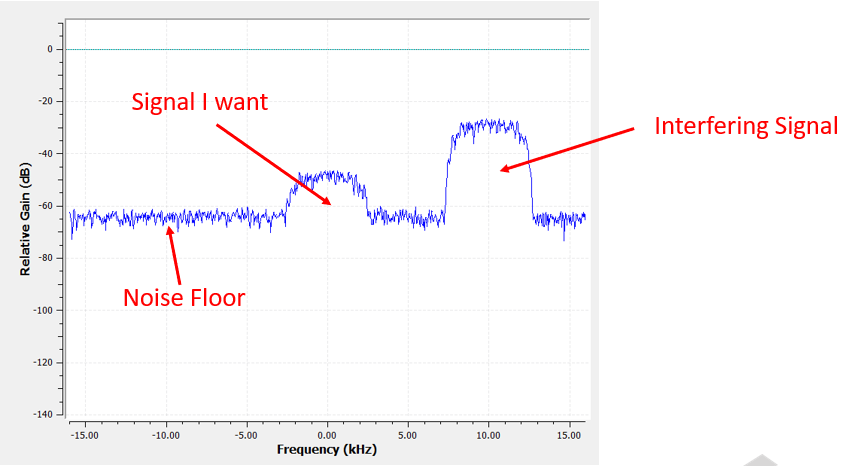
因为我们的信号已经集中在直流(0 Hz)上,所以需要一个低通滤波器。 选择滤波器就必须确定一个 “截止频率(Cutoff Frequency)”(也称为转折频率 Conor Frequency),这将决定通带在频谱的哪里过渡到阻带。 截止频率的单位始终是 Hz,在这个例子中,3 kHz 似乎是一个不错的值:
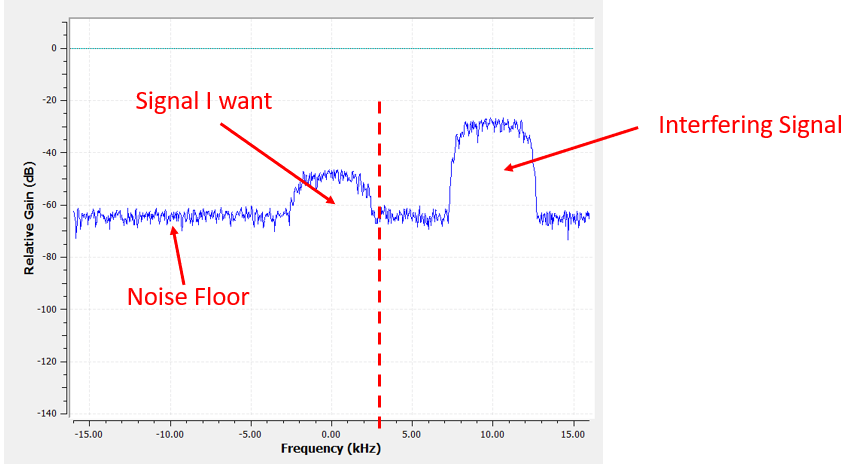
然而,按照大多数低通滤波器的工作方式,在负频率处也会有一个 -3 kHz 的边界,即它关于直流会表现出对称性(稍后你会明白为什么)。 所以,我们的截止频率看起来像这样(两者之间的区域就是通带):
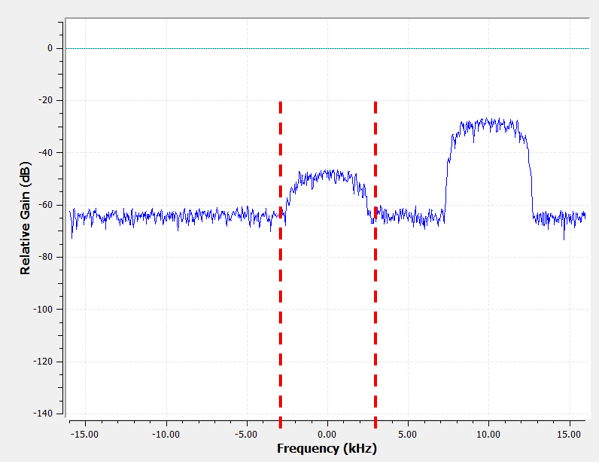
在创建并应用截止频率为 3 kHz 的滤波器后,我们将得到:
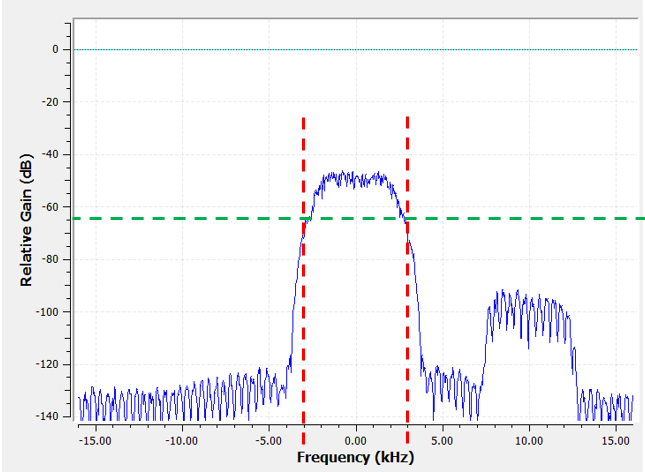
这个滤波后的信号看起来可能仍然让人有些困惑。但是,如果你回看原信号,你会发现噪音功率 原本 在 -65 dB 左右(图中绿色虚线),而现在已经被大大降低(滤除)。 尽管在 10 kHz 处的干扰信号仍然部分存在,但是我们已经 大幅 降低了它的功率,使其低于背景噪音功率(绿色虚线)。 可以说,我们滤除了阻带中存在的大部分噪音。
除了截止频率,我们的低通滤波器的另一个主要参数称为 “过渡带宽(Transition Width)”。 过渡带宽同样以 Hz 为单位,指示滤波器在通带和阻带之间转换的速度(译者注:此速度指的是频域上的频率变化速度),因为瞬时转换是不可能的。
让我们可视化过渡带宽。在下图中,绿色 线代表了在通带和阻带之间过渡的理想响应,它基本上具有零的过渡带宽。红色 线展示了一个现实滤波器的结果,它有一些波纹(Ripple)和一定的过渡带宽。
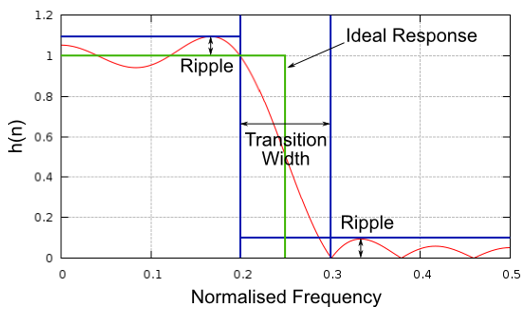
你可以会好奇,我们能否把这个过渡带宽控制的尽可能窄呢?实际上是困难的,因为更小的过渡带宽需要更长的滤波器抽头 — 更多的计算量。 举一个具体的例子:一个 50 抽头的滤波器可以在树莓派上运行一整天而只占用 1% 的 CPU,然而一个 50,000 抽头的滤波器则会让你的 CPU 爆满! 通常我们会使用设计工具设计一个滤波器,然后查看它输出了多少抽头,如果太多(例如,超过 100 个),我们会增加过渡带宽。 当然,具体的取舍取决于应用场景和运行滤波器的硬件。
在上面的滤波示例中,我们使用了 3 kHz 的截止频率和 1 kHz 的过渡带宽(仅通过截图其实不容易看出来)。最终的滤波器有 77 个抽头。
回到滤波器的表示。尽管我们可以用抽头列表来表示滤波器,但我们通常在频域中以图形方式表示滤波器。 我们称之为滤波器的 “频率响应(Frequency Response)”,它展示了滤波器对不同频率的行为。 以下是我们刚刚使用的滤波器的频率响应:
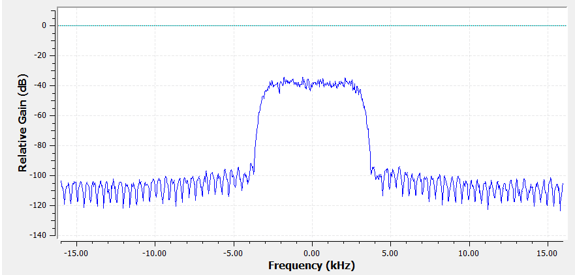
请注意,上图并不是一个信号,而是滤波器的频域表示。这可能一开始有点难以理解,但随着我们深入后文的示例和代码,它会变得清晰。
一个给定的滤波器也可以在时域里表示;它被称为滤波器的 “脉冲响应”,因为如果你把一个脉冲通过这个滤波器的话,这就是你在时域中将看到的结果。(搜索 “狄拉克三角函数” 可了解更多有关脉冲的信息)。 对于 FIR 型滤波器来说,脉冲响应就是抽头本身。对于我们之前使用的 77 个抽头的滤波器,抽头为
h = [-0.00025604525581002235, 0.00013669139298144728, 0.0005385575350373983,
0.0008378280326724052, 0.000906112720258534, 0.0006353431381285191,
-9.884083502996931e-19, -0.0008822851814329624, -0.0017323142383247614,
-0.0021665366366505623, -0.0018335371278226376, -0.0005912294145673513,
0.001349081052467227, 0.0033936649560928345, 0.004703888203948736,
0.004488115198910236, 0.0023609865456819534, -0.0013707970501855016,
-0.00564080523326993, -0.008859002031385899, -0.009428252466022968,
-0.006394983734935522, 4.76480351940553e-18, 0.008114570751786232,
0.015200719237327576, 0.018197273835539818, 0.01482443418353796,
0.004636279307305813, -0.010356673039495945, -0.025791890919208527,
-0.03587324544787407, -0.034922562539577484, -0.019146423786878586,
0.011919975280761719, 0.05478153005242348, 0.10243935883045197,
0.1458890736103058, 0.1762896478176117, 0.18720689415931702,
0.1762896478176117, 0.1458890736103058, 0.10243935883045197,
0.05478153005242348, 0.011919975280761719, -0.019146423786878586,
-0.034922562539577484, -0.03587324544787407, -0.025791890919208527,
-0.010356673039495945, 0.004636279307305813, 0.01482443418353796,
0.018197273835539818, 0.015200719237327576, 0.008114570751786232,
4.76480351940553e-18, -0.006394983734935522, -0.009428252466022968,
-0.008859002031385899, -0.00564080523326993, -0.0013707970501855016,
0.0023609865456819534, 0.004488115198910236, 0.004703888203948736,
0.0033936649560928345, 0.001349081052467227, -0.0005912294145673513,
-0.0018335371278226376, -0.0021665366366505623, -0.0017323142383247614,
-0.0008822851814329624, -9.884083502996931e-19, 0.0006353431381285191,
0.000906112720258534, 0.0008378280326724052, 0.0005385575350373983,
0.00013669139298144728, -0.00025604525581002235]
尽管我们还没有开始讲滤波器设计,但可以先看看生成该滤波器的 Python 代码:
import numpy as np
from scipy import signal
import matplotlib.pyplot as plt
num_taps = 51 # 使用奇数个抽头
cut_off = 3000 # Hz
sample_rate = 32000 # Hz
# 创建低通滤波器
h = signal.firwin(num_taps, cut_off, fs=sample_rate)
# 绘制脉冲响应
plt.plot(h, '.-')
plt.show()
只需把这个浮点数组绘制出来,就得到了这个滤波器的脉冲响应:
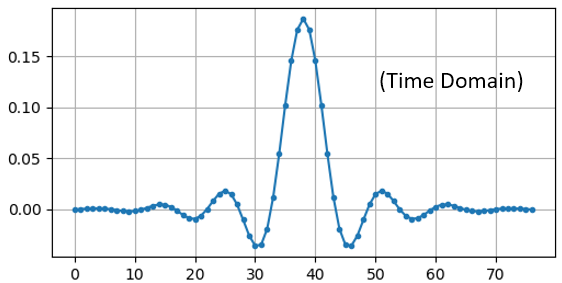
这里是用于生成之前显示的频率响应的代码。它稍微复杂一些,因为我们需要创建以频率为 x 轴的数组。
# 绘制频率响应
H = np.abs(np.fft.fft(h, 1024)) # 进行窗口长度为 1024 的 FFT,记录幅度
H = np.fft.fftshift(H) # 将 0 Hz 移到中间
w = np.linspace(-sample_rate/2, sample_rate/2, len(H)) # x 轴
plt.plot(w, H, '.-')
plt.show()
实数和复数滤波器¶
上文展示过的滤波器都是实数抽头,但是抽头其实也可以是复数。 抽头是实数还是复数并不一定要与输入信号匹配,也就是说,你可以将复数信号通过具有实数抽头的滤波器,反之亦然。 当抽头是实数时,滤波器的频率响应将在直流(0 Hz)周围对称。 一般而言我们只在需要不对称性时才使用复数抽头,但这种情况并不常见。

作为复数抽头滤波器的例子,让我们回到之前的滤波使用案例,这次我们想接收另一个干扰信号(而不必重新调谐收音机)。 这意味着我们需要一个带通滤波器,但是它并不是关于直流对称的。 我们只想保留(即 “通过”)大约 7 kHz 到 13 kHz 之间的频率(同时不希望通过 -13 kHz 到 -7 kHz 的频率):
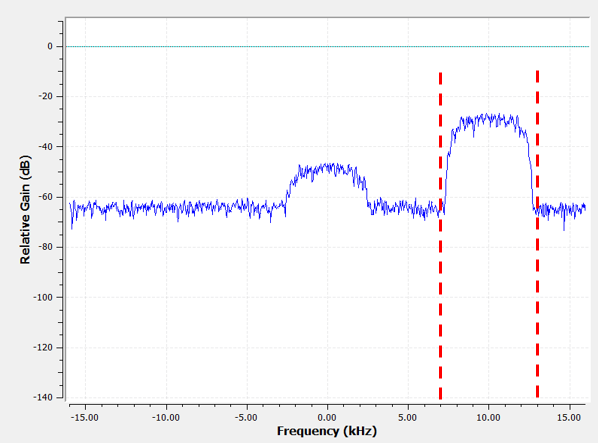
一种设计方法是首先建立一个截止频率为 3 kHz 的低通滤波器,然后将它频移。 如果你还记得,我们可以将 \(x(t)\) 乘以 \(e^{j2\pi f_0t}\) 来频移 \(f_0\) 。 具体而言这里 \(f_0\) 取 10 kHz。 前面 Python 示例代码中,\(h\) 就是我们创建的原本的低通滤波器的抽头。 为了创建带通滤波器,只需将这些抽头乘以 \(e^{j2\pi f_0t}\) ,同时需要根据采样周期(采样率的倒数)创建一个向量来储存时间值:
# (h 来自前文代码示例)
# 通过乘以 exp(j*2*pi*f0*t) 进行频移
f0 = 10e3 # 频移的量(Hz)
Ts = 1.0/sample_rate # 采样时间
t = np.arange(0.0, Ts*len(h), Ts) # 时间向量,(start, stop, step)
exponential = np.exp(2j*np.pi*f0*t) # 这里本质上是一个正弦波
h_band_pass = h * exponential # 将低通滤波器进行频移,得到带通滤波器
# 绘制脉冲响应
plt.figure('impulse')
plt.plot(np.real(h_band_pass), '.-')
plt.plot(np.imag(h_band_pass), '.-')
plt.legend(['real', 'imag'], loc=1)
# 绘制频率响应
H = np.abs(np.fft.fft(h_band_pass, 1024)) # 进行窗口长度为 1024 的 FFT,记录幅度
H = np.fft.fftshift(H) # 将 0 Hz 移到中间
w = np.linspace(-sample_rate/2, sample_rate/2, len(H)) # x 轴
plt.figure('freq')
plt.plot(w, H, '.-')
plt.xlabel('Frequency [Hz]')
plt.show()
脉冲响应和频率响应图如下所示:
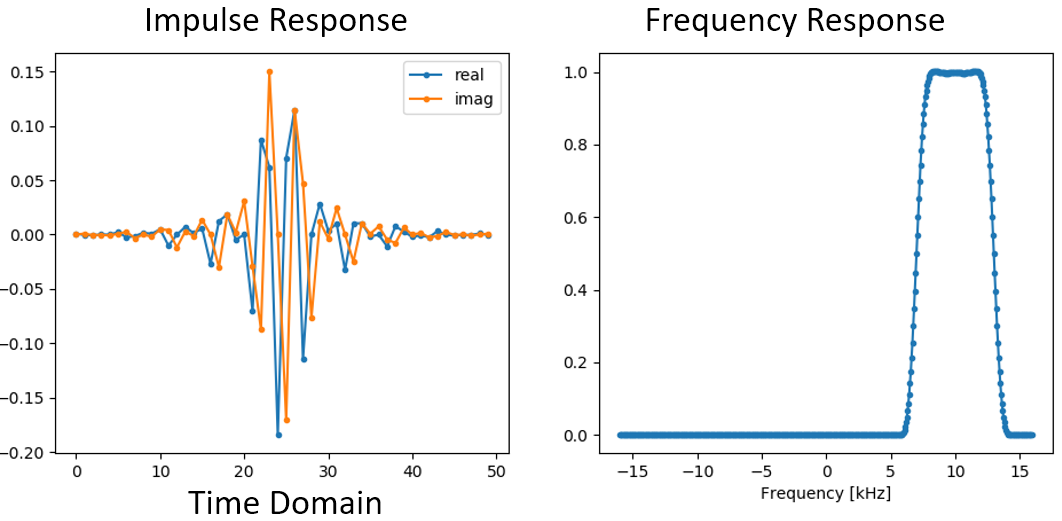
此时,我们的滤波器不再是关于 0 Hz 对称的,因此其抽头必然为复数。 在左图(脉冲响应)中,我们需要分别用两条线绘制实部和虚部。 而右图(频率响应)则清晰地展示了我们的滤波器确实实现了目标中的带通效果 — 它有效地滤除了集中在 10 kHz 的信号以外的所有内容。 再次提醒,上述图示 并不是 实际信号;它仅仅是滤波器的表示。 然而,这一区别可能相当微妙,因为在许多情况下,当你将滤波器应用于信号并在频域中绘制输出时,结果可能与滤波器的频率响应看起来大致相同。
如果这个小节让你感到困惑,不用担心,99% 的情况下你只需要处理简单的低通滤波器,它们的抽头都是实数的。
卷积¶
我们将简短地介绍一下卷积运算。如果你已经熟悉它,可以跳过这一部分。
将两个信号相加是将它们合并为一个的简单方法。在 频率域 章节中,我们探讨了如何在线性系统中将两个信号相加。
卷积是另一种将两个信号结合的方法,但与简单相加有很大的不同。
卷积运算的本质是将一个信号滑动到另一个信号上,然后进行积分。
如果你熟悉互相关操作,你会发现卷积和它非常相似。实际上,在许多情况下,卷积和互相关是等价的。
我们通常用 * 符号来表示卷积,特别是在数学表达式中。
我认为学会卷积操作的最佳方式是通过示例。在这个第一个例子中,我们将介绍两个方形波的卷积:
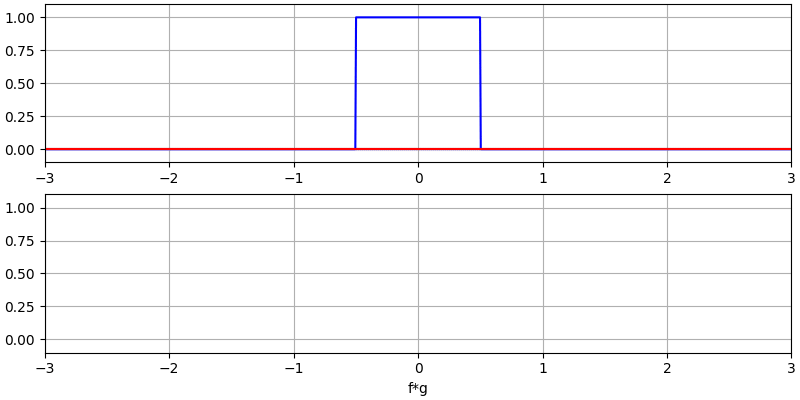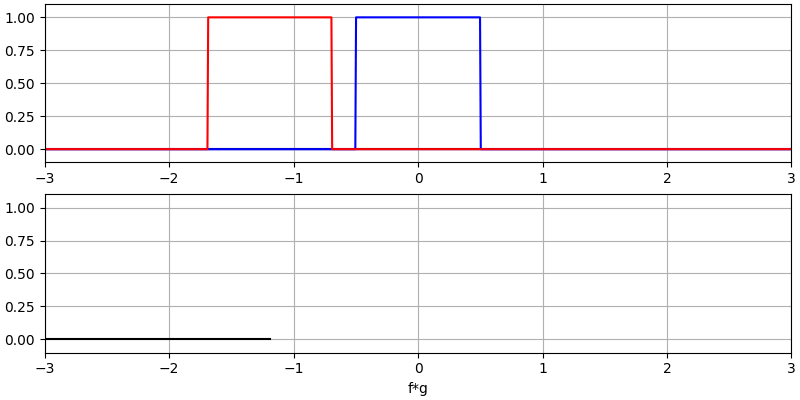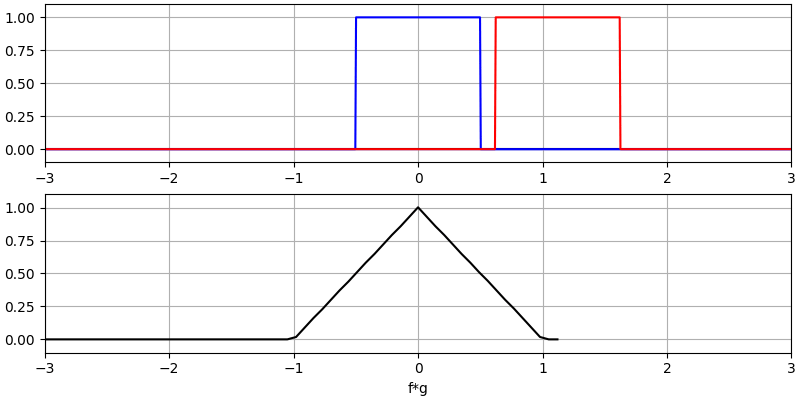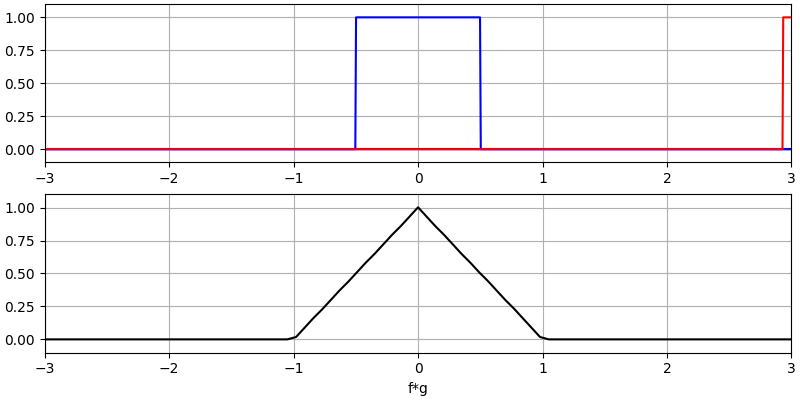
我们有两个输入信号(一个红色,一个蓝色),其卷积的输出显示为黑色。 你可以看到,当一个信号滑过另一个信号时,输出是两个信号的积分。 由于这只是一个滑动积分,结果是一个三角形,最大值出现在两个方形脉冲完美对齐的点。
让我们再看看几个卷积的例子:
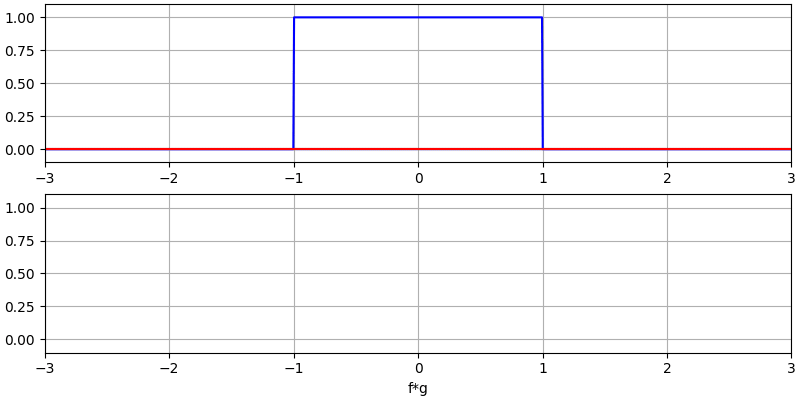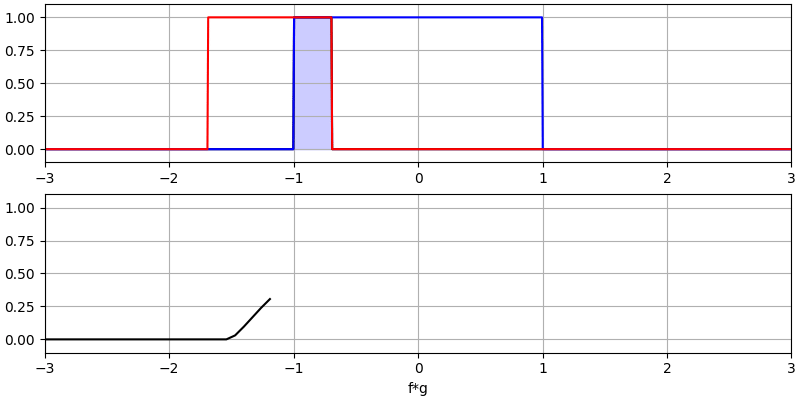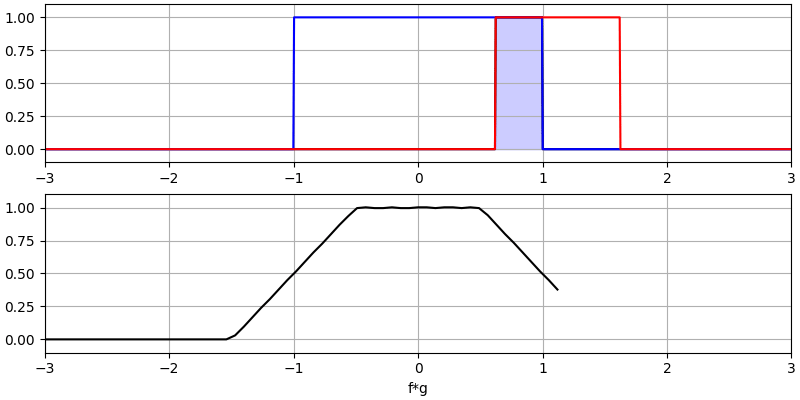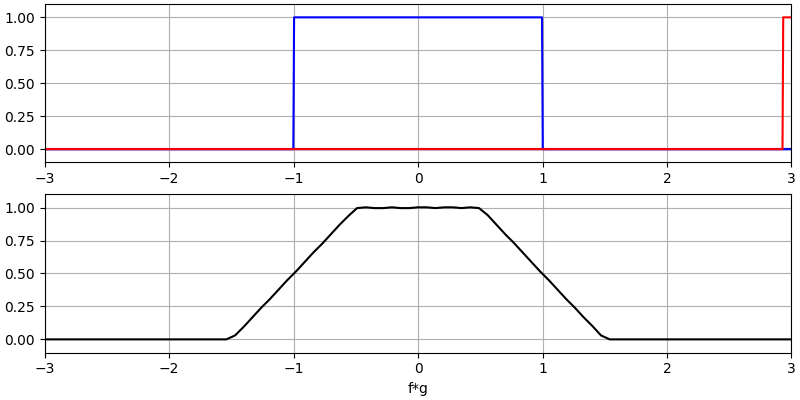
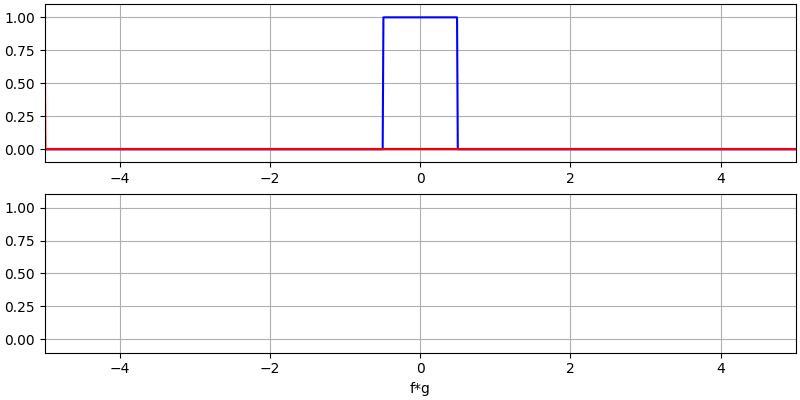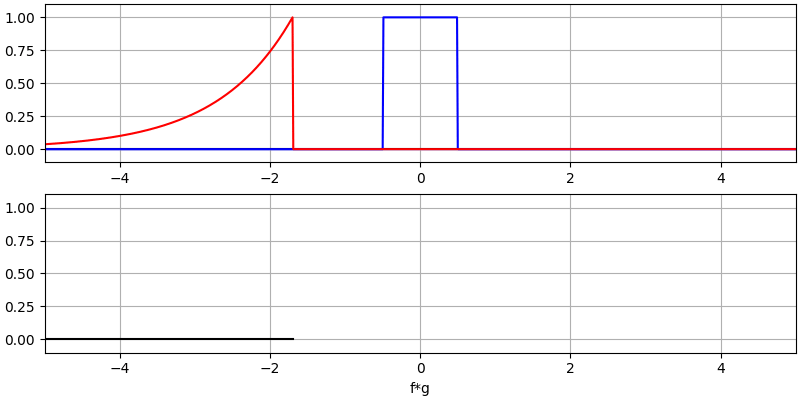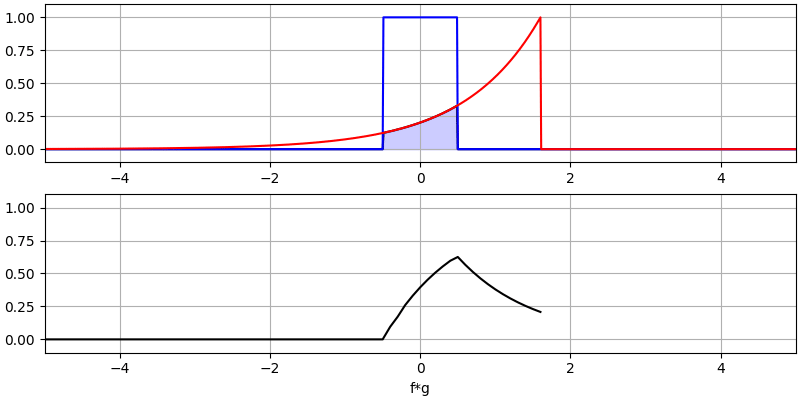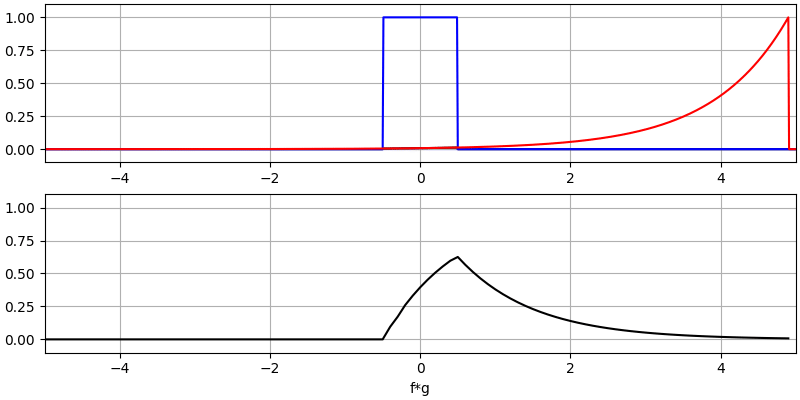
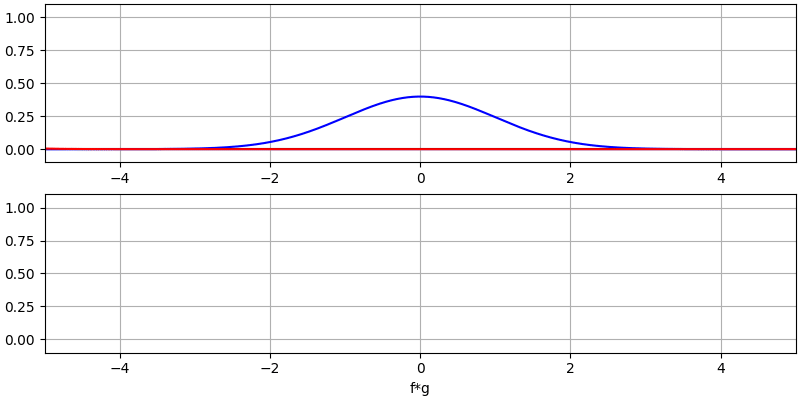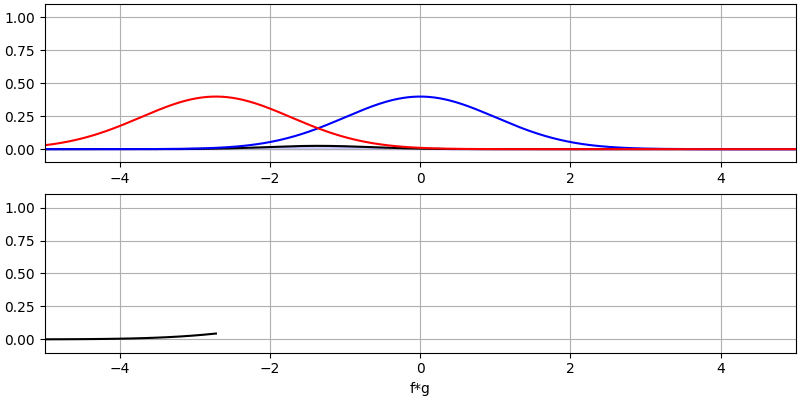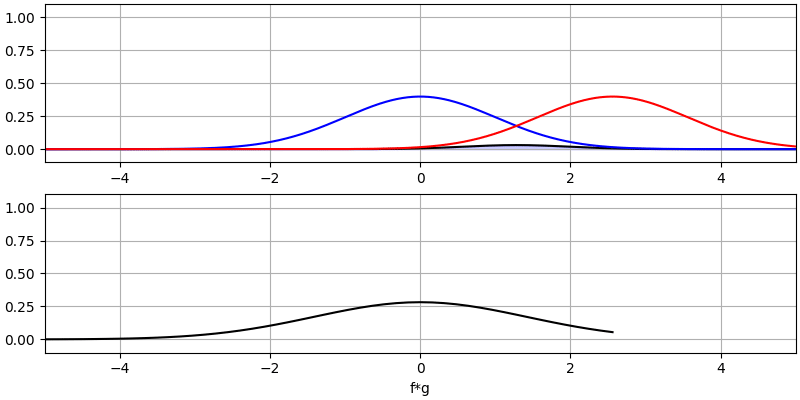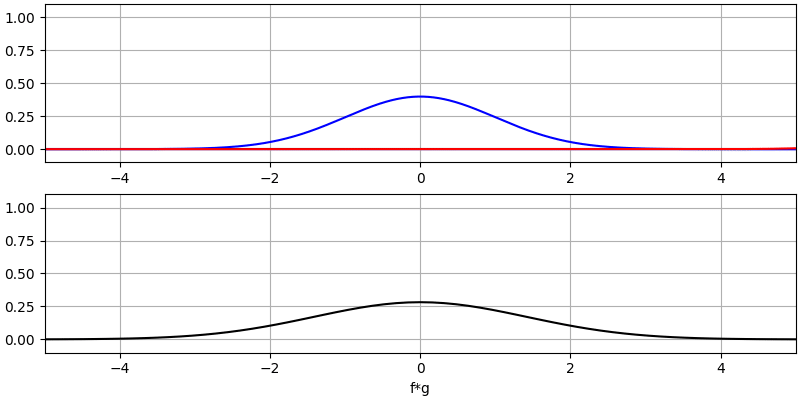
注意,高斯与高斯的卷积仍然是一个高斯函数,但具有更宽的脉冲和更低的幅度。
由于这种 “滑动” 特性,输出的长度实际上比输入的长度更长。如果一个信号是 M 个样本,另一个信号是 N 个样本,这两个信号的卷积可以产生 N+M-1 个样本。
像 numpy.convolve() 这样的函数可以指定您想要整个输出( max(M, N) 个样本)还是仅仅是信号完全重叠的样本( max(M, N) - min(M, N) + 1 )。
有点复杂,但是你其实不需要纠结于这个细节,只需知道卷积的输出长度不仅仅是输入的长度。
那么卷积在数字信号处理(DSP)中为什么重要呢?首先,要对信号进行滤波,我们可以简单地取该滤波器的脉冲响应并与信号进行卷积。FIR 滤波实际上就是一个卷积操作。
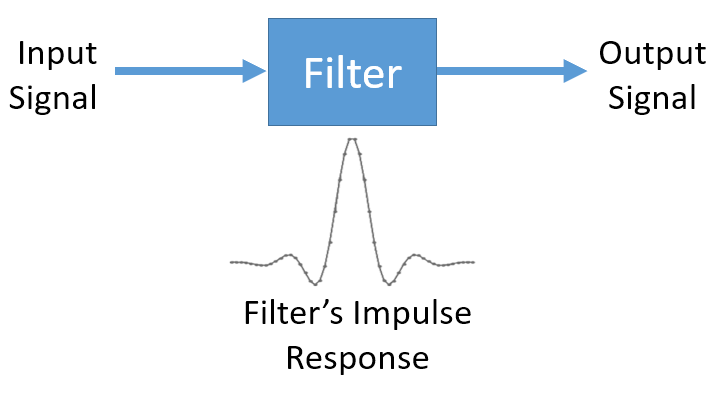
说滤波器是卷积操作可能有点不好理解,因为我们在前面提到,卷积计算要输入两个信号并输出一个信号。 可以试着这么理解:我们将滤波器的脉冲响应视为一个信号,而卷积就是一个数学运算符,它对两个一维数组进行运算。 如果其中一个一维数组是滤波器的脉冲响应,那么另一个一维数组可以是一段输入信号,而输出则是输入信号的被滤波后的结果。
让我们再看一个例子来帮助理解。在下面的示例中,三角形代表滤波器的脉冲响应,而 绿色 信号则是要被滤波的信号。
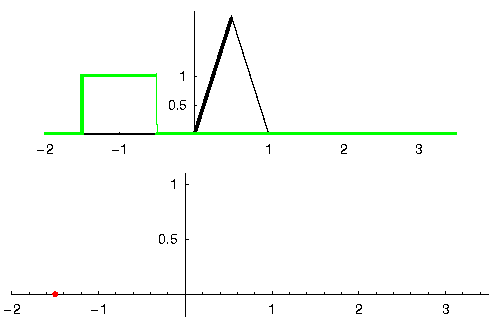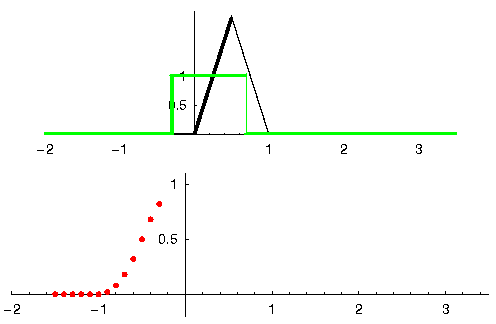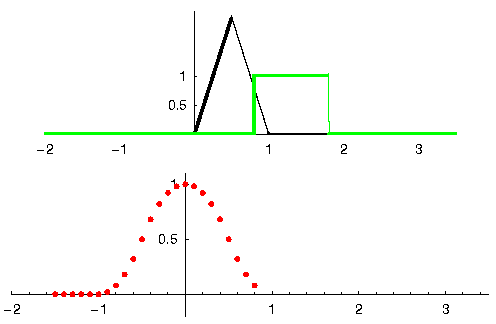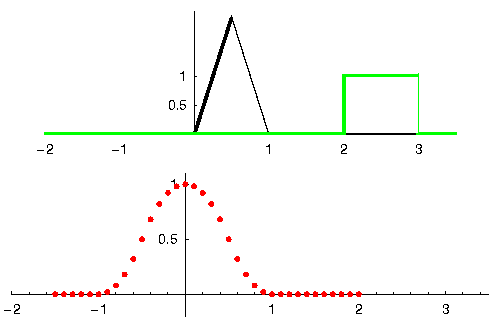
红色 是滤波后的信号。
问:三角形的脉冲响应是来自什么类型的滤波器?
Answers
它平滑了绿色信号的高频成分(即方波的急剧变化的部分),因此起到了低通滤波器的作用。
现在我们对卷积已经有些了解了,那么就来介绍一下卷积的数学公式。星号 (*) 通常用作表示卷积的符号:
在上式中,\(g(t)\) 是时间上颠倒并滑过 \(f(t)\) 的信号或输入,但 \(g(t)\) 和 \(f(t)\) 可以互换,仍然是相同的表达式。 通常,较短的数组将被当作 \(g(t)\) 。 当 \(g(t)\) 是对称的,即相对于原点翻转时不变,卷积等于互相关,上式可写为 \(\int f(\tau) g(t+\tau)\) 。
滤波器的实现¶
我们并不会太深入地探讨滤波器的实现,相反,将专注于介绍滤波器的设计(反正你可以在任何编程语言中找到现成可用的实现)。 就目前而言,记住一个要点:使用 FIR 滤波器滤波信号时,就是把脉冲响应(抽头数组)与输入信号卷积即可。 在离散信号的世界中,我们使用离散卷积(如下图所示)。 标记着 \(b\) 的那些三角形表示抽头。 在这个流程图中,三角形上方标有 \(z^{-1}\) 的正方形表示延迟一个时间步长。
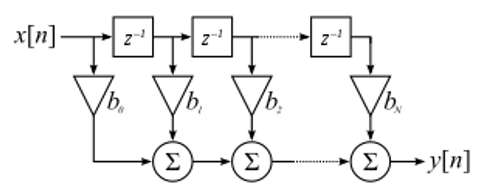
从这个图里也许你能理解为什么叫滤波器的 “抽头(taps)”,与图里所示的滤波器的实现方式有关。
FIR 与 IIR¶
数字滤波器有两大类:FIR 和 IIR
- 有限脉冲响应(Finite Impulse Response,FIR)
- 无限脉冲响应(Infinite Impulse Response,IIR)
我们不对理论进行太深入的研究,但现在只需记住以下几点:FIR 滤波器更容易设计,只要使用足够多的抽头,就能实现任何你想要做的事情。 IIR 滤波器更为复杂,有可能不稳定,但效率更高(对于给定的滤波器,CPU 和内存的使用量更少)。 如果有人丢给你一个抽头的浮点数数组,那应该就是一个FIR滤波器。如果他们开始提到 “极点(poles)”,那么他们说的就是 IIR 滤波器。在本书中,我们只重点关注 FIR 滤波器。
下面是一个频率响应示例,比较的是两个效果几乎一样的 FIR 和 IIR 滤波器;它们具有相似的过渡带宽,而我们前面讲过过渡带宽将决定需要多少个抽头。 这个 FIR 滤波器有 50 个抽头,而 IIR 滤波器有 12 个极点,就所消耗的计算资源而言,这就相当于12个抽头。
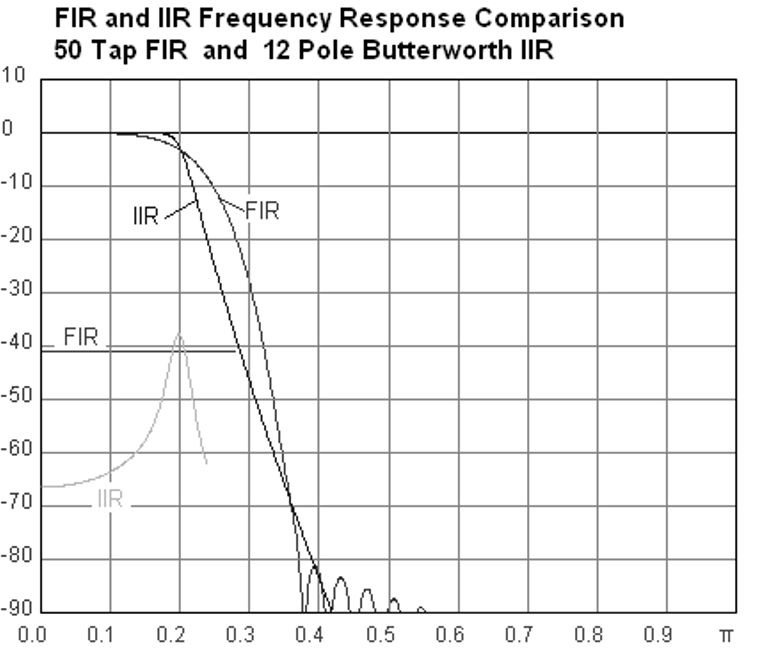
经验告诉我们,要执行大致相同的滤波操作,FIR 滤波器所需的计算资源要比IIR滤波器多得多。
下面是一些你可能实际用过的 FIR 和 IIR 滤波器的例子。
如果对一个数组进行 “滑动平均”,这就是一个抽头全为 1 的 FIR 滤波器: \(- h = [1 1 1 1 1 1 1 1 1 1]\) ,表示窗口大小为 10 的滑动平均滤波器。它恰好也是一个低通滤波器,为什么?使用全是 1 的和逐渐衰减到零的抽头有什么区别?
Answers
滑动平均滤波器是一种低通滤波器,因为它能平滑掉 “高频” 变化,这通常也是人们使用这种滤波器的原因。 使用两端衰减到零的抽头是为了避免输出突然变化,比如被滤波的信号在一段时间内为零,然后突然跃升这种情况。
现在举一个 IIR 例子。你平时有没有做过类似这样的操作?
x = x*0.99 + new_value*0.01
其中 0.99 和 0.01 代表数值更新的速度(或衰减率,是一个意思)。 这是可以缓慢更新某个变量的一种简便方法,同时无需记住 x 的历史数值。这实际上是一种低通 IIR 滤波器。 希望从这个例子你能明白为什么 IIR 滤波器的稳定性不如 FIR 滤波器。 因为历史数值的影响永远不会完全消失!
FIR 滤波器设计¶
在实践中,大多数人会使用滤波器设计工具或代码中的函数(如 Python/SciPy)来设计滤波器。 我们将首先展示在 Python 中可以实现的功能,然后再介绍第三方工具。 我们的重点将放在 FIR 滤波器上,因为这是当前数字信号处理中最常用的滤波器。
Python 代码¶
设计滤波器就是要得到满足我们所需的频率相应的抽头,其中关键一环是要确定滤波器的类型(低通、高通、带通或带阻)、截止频率、抽头数量以及过渡带宽。
在 SciPy 中,我们主要使用两个函数来设计 FIR 滤波器,这两个函数都使用所谓的窗口方法。
首先, scipy.signal.firwin() 是最直接的,它能给出线性相位FIR滤波器的抽头。
该函数需要我们指定抽头数和一个截止频率(用于低通/高通),或者两个截止频率(用于带通/带阻),还可以选择指定过渡带宽。
如果通过 fs 指定采样率,则截止频率和过渡带宽的单位为Hz,但如果不指定采样率,则单位为归一化的 Hz(0 至 1 Hz)。
默认情况下, pass_zero 参数为 True ,但如果需要高通或带通滤波器,则必须将其设置为 False ;它表示通带中是否应包含 0 Hz。
建议使用奇数个抽头,101 个抽头是一个很好的起点。
例如,让我们生成一个采样率为 1 MHz、通带范围为 100 kHz 至 200 kHz 的带通滤波器:
from scipy.signal import firwin
sample_rate = 1e6
h = firwin(101, [100e3, 200e3], pass_zero=False, fs=sample_rate)
print(h)
第二个函数是 scipy.signal.firwin2() ,它更加灵活,可用于设计具有自定义频率响应的滤波器,因为可以指定多个频率以及每个频率上所需的增益。
它也要求提供抽头数,并支持上一段提到的 fs 参数。
例如,下面的代码生成的滤波器具有一个低通区域,使 100 kHz以下的频率可以通过,还具有一个带通区域,200 kHz 至 300 kHz,但这里的增益是低通区域的一半,同时要求过渡带宽为 10 kHz:
from scipy.signal import firwin2
sample_rate = 1e6
freqs = [0, 100e3, 110e3, 190e3, 200e3, 300e3, 310e3, 500e3]
gains = [1, 1, 0, 0, 0.5, 0.5, 0, 0]
h2 = firwin2(101, freqs, gains, fs=sample_rate)
print(h2)
要在信号上实际使用 FIR 滤波器,有以下几个函数可选择使用,但它们实际上都是在要滤波的采样点和上面生成的滤波器抽头之间进行卷积操作:
np.convolvescipy.signal.convolvescipy.signal.fftconvolvescipy.signal.lfilter
上述基于卷积的函数都有一个 mode 参数,可以选择 'full'、'valid' 或 'same' ,它们的作用是会影响函数输出数据量的大小。
因为在执行卷积时,正如我们在本章前面所看到的,在开始和结束时会产生过渡值。使用 'valid' 选项将不会产生这些过渡值,输出数据的大小就会比输入信号略小。
如果使用 'same' 选项,输出数据将与输入信号大小相同,这在追踪时间或其他时域信号特征时非常有用。最后,'full' 选项将包括所有的过渡值,输出完整的卷积结果。
现在,我们将基于 scipy.signal.firwin2() 生成的抽头,使用上面的四个函数处理一个由高斯白噪声构成的测试信号。
请注意, lfilter 有一个额外的参数(第二个参数),对于 FIR 滤波器来说,这个参数总是1。
import numpy as np
from scipy.signal import firwin2, convolve, fftconvolve, lfilter
# 创建一个信号用于测试,我们在这里采用高斯噪音
sample_rate = 1e6 # Hz
N = 1000 # samples to simulate
x = np.random.randn(N) + 1j * np.random.randn(N)
# 创建一个 FIR 滤波器,与上文第二个示例相同
freqs = [0, 100e3, 110e3, 190e3, 200e3, 300e3, 310e3, 500e3]
gains = [1, 1, 0, 0, 0.5, 0.5, 0, 0]
h2 = firwin2(101, freqs, gains, fs=sample_rate)
# 使用四种方法应用滤波器
x_numpy = np.convolve(h2, x)
x_scipy = convolve(h2, x) # scipys convolve
x_fft_convolve = fftconvolve(h2, x)
x_lfilter = lfilter(h2, 1, x) # 2nd arg is always 1 for FIR filters
# 验证它们的输出均相同
print(x_numpy[0:2])
print(x_scipy[0:2])
print(x_fft_convolve[0:2])
print(x_lfilter[0:2])
上述代码展示了这四个函数的基本用法,但你可能想知道哪种方法最好。 当这四种方法在英特尔酷睿 i9-10900K 上运行时,下面的图显示了使用不同数量的抽头时所耗费的计算时间,两个图分别是处理 1k 个和 100k 个采样点的情况。
可以看到,scipy.signal.convolve 实际上是在输入数据达到一定大小时自动切换为基于 FFT 的方法。
总的来说,对于给定的抽头和输入数据量(代表射频应用中相当典型的数据量大小), fftconvolve 都是明显的赢家。
PySDR 中的许多代码实际上都使用 np.convolve: ,这只是因为它不需要导入 scipy 库,并且对于低数据率或非实时应用来说,性能差异可以忽略不计。
最后,我们将在频域显示输出,以便最终确认 firwin2 方法是否为我们提供了与设计参数相匹配的滤波器。从上面生成 h2 的代码开始:
# 创建模拟信号,包含高斯噪音
N = 100000 # 信号长度
x = np.random.randn(N) + 1j * np.random.randn(N) # 复数信号
# 保存输入信号的 PSD
PSD_input = 10*np.log10(np.fft.fftshift(np.abs(np.fft.fft(x))**2)/len(x))
# 应用滤波器
x = fftconvolve(x, h2, 'same')
# 查看输出信号的 PSD
PSD_output = 10*np.log10(np.fft.fftshift(np.abs(np.fft.fft(x))**2)/len(x))
f = np.linspace(-sample_rate/2/1e6, sample_rate/2/1e6, len(PSD_output))
plt.plot(f, PSD_input, alpha=0.8)
plt.plot(f, PSD_output, alpha=0.8)
plt.xlabel('Frequency [MHz]')
plt.ylabel('PSD [dB]')
plt.axis([sample_rate/-2/1e6, sample_rate/2/1e6, -40, 20])
plt.legend(['Input', 'Output'], loc=1)
plt.grid()
plt.savefig('../_images/fftconvolve.svg', bbox_inches='tight')
plt.show()
我们可以看到,带通部分比低通部分低 3 dB :
另外,还有一个不起眼的函数用于对信号进行滤波,叫做 scipy.signal.filtfilt。
它实现的是 “零相位滤波”,有助于保留时域波形中的一些特征,使这些特征在滤波后和滤波前的信号中出现的位置保持不变。
它通过使用两次滤波器抽头来实现这一点,正向使用一次,然后再反向使用一次。
此时,频率响应将是正常情况下的平方。
更多信息,请参阅 https://www.mathworks.com/help/signal/ref/filtfilt.html 或 https://docs.scipy.org/doc/scipy/reference/generated/scipy.signal.filtfilt.html。
状态滤波(Stateful Filtering)¶
如果你正在创建一个实时应用程序,需要依次对采样数据块应用滤波函数,这时,能保存状态的滤波器就会非常有用。
使用这种滤波器时,可以用上一次调用滤波器的输出提供这一次调用的初始条件。
这样可以消除信号开始和结束时出现的过渡变化(毕竟,在程序连续运行时,输入滤波器的采样数据块实际是连续的)。
状态必须在两次调用之间保存,而且还必须在代码一开始就初始化,以便进行第一次滤波器的调用。
幸运的是,SciPy 中的 lfilter_zi 可以为 lfilter 构造初始条件。
下面展示一个使用有状态滤波器处理连续采样数据的示例:
b = taps
a = 1 # 对于 FIR 是 1,对于 IIR 不是 1
zi = lfilter_zi(b, a) # 计算初始条件
while True:
samples = sdr.read_samples(num_samples) # 请换成你自己的 SDR 设备的采样代码
samples_filtered, zi = lfilter(b, a, samples, zi=zi) # 应用滤波器
第三方工具¶
还可以使用 Python 以外的工具来设计自定义 FIR 滤波器。 对于学生,我推荐 Peter Isza 设计的这款简单易用的网络应用程序,它可以显示脉冲响应和频率响应:http://t-filter.engineerjs.com。 使用默认值,至少在撰写本文时,它就会设计一个低通滤波器,通带为 0 至 400 Hz,阻带为 500 Hz 及以上。因为采样率为 2 kHz,所以我们能 “看到” 的最大频率为 1 kHz。
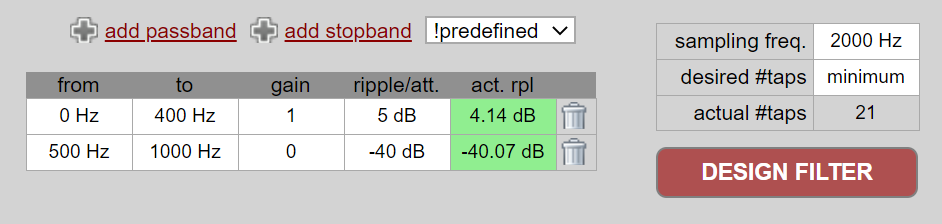
点击 “设计滤波器” 按钮,创建抽头并绘制频率响应图。
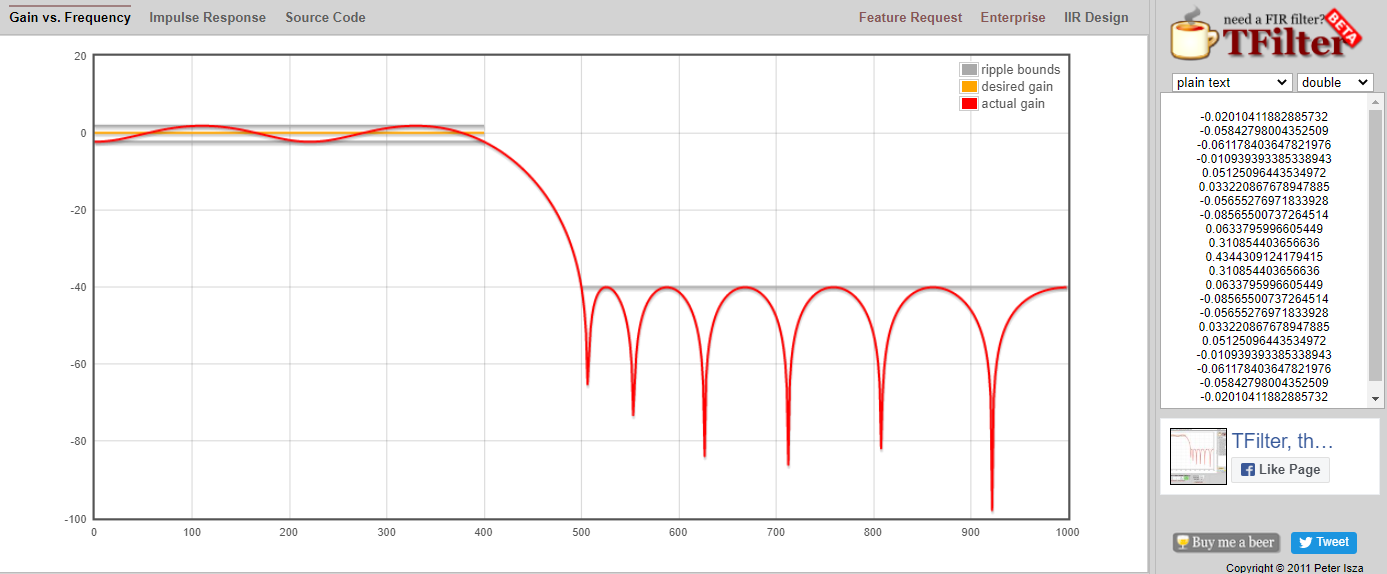
单击图上方的 “脉冲响应” 标签,查看脉冲响应,因为这是一个 FIR 滤波器,所以这里显示的是抽头的图。
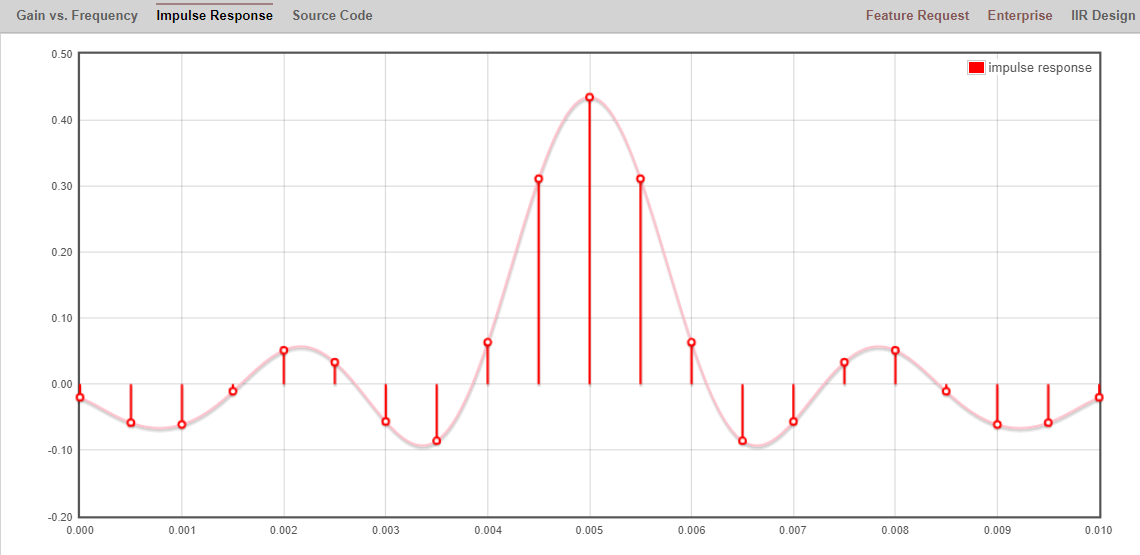
该应用程序甚至包括实现和使用该滤波器的 C++ 源代码。网络应用程序不包括任何设计 IIR 滤波器的方法,设计 IIR 滤波器一般要困难得多。
任意频率响应¶
现在,我们考虑一种用 Python 自行设计 FIR 滤波器的方法,从所需的频率响应开始,倒推找到脉冲响应。最终显示出我们的滤波器(通过画出其抽头的图)。
首先,创建一个所需的频率响应矢量。让我们设计一个任意形状的低通滤波器,如下图所示:
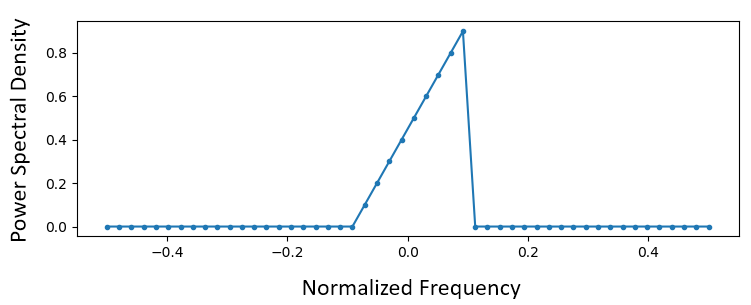
用于创建此滤波器的代码相当简单:
import numpy as np
import matplotlib.pyplot as plt
H = np.hstack((np.zeros(20), np.arange(10)/10, np.zeros(20)))
w = np.linspace(-0.5, 0.5, 50)
plt.plot(w, H, '.-')
plt.show()
hstack() 是在 numpy 中连接数组的一种方法。我们知道它会最终产生一个具有复数抽头的过滤器。为什么?
Answer
因为我们要求的频率响应并不以 0 Hz 对称。
我们的最终目标是找到该滤波器的抽头,以便实际使用。给定了频率响应,如何得到抽头呢?嗯,想想我们一般如何把信号从频域转换回时域呢?反向 FFT (IFFT)!回想一下,IFFT 函数与 FFT 函数几乎完全相同。我们还需要在 IFFT 之前对所需频率响应调用 IFFTshift,然后在 IFFT 之后再进行一次 IFFTshift(不,它们不会互相抵消,你可以试试)。这个过程可能看起来令人困惑。但请记住,在 FFT 之后总要进行 FFTshift,而在 IFFT 之后总要进行 IFFTshift。
h = np.fft.ifftshift(np.fft.ifft(np.fft.ifftshift(H)))
plt.plot(np.real(h))
plt.plot(np.imag(h))
plt.legend(['real','imag'], loc=1)
plt.show()
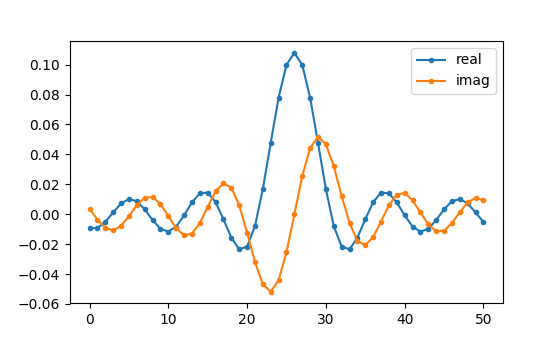
我们将使用上面显示的抽头作为滤波器。我们知道画出抽头就是脉冲响应,所以我们在上面看到的就是脉冲响应。让我们对抽头进行 FFT,看看频域的情况。进行 1,024 点 FFT,以获得高分辨率:
H_fft = np.fft.fftshift(np.abs(np.fft.fft(h, 1024)))
plt.plot(H_fft)
plt.show()
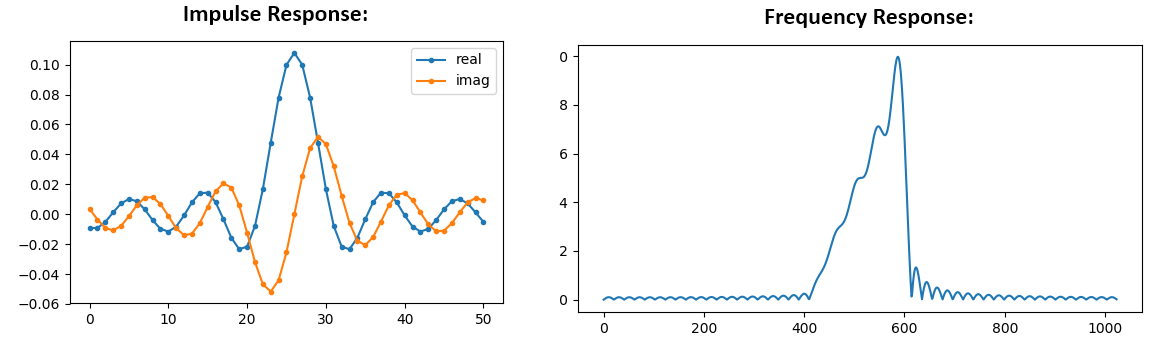
看,频率响应并不平直。。。如果你还记得我们最初设想的滤波器,那么它并不符合我们的期望。其中一个重要原因是我们的脉冲响应没有做到衰减,也就是说,左右两边的频率响应没有达到零。我们有两种方法可以让它衰减为零:
方法 1: 我们对当前的脉冲响应加窗,使其两边都衰减为 0。这需要将脉冲响应与一个起点和终点均为 0 的 “窗口函数” 相乘。
# 上文示例中我们创建了 h,现在创建并应用窗口
window = np.hamming(len(h))
h = h * window
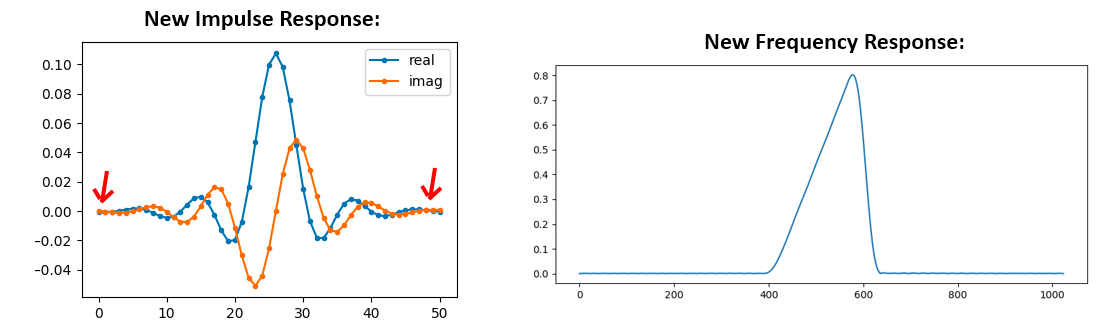
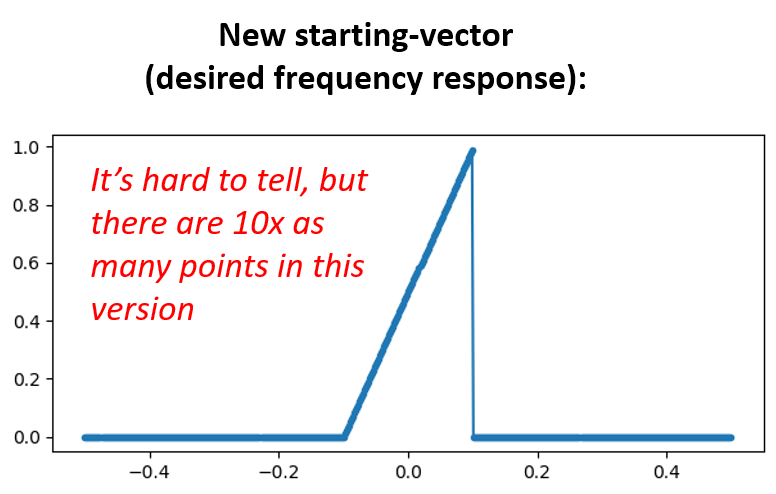
方法 2: 我们使用更多的点重新生成脉冲响应,使其有时间衰减。我们需要在原始频域数组中增加分辨率(称为内插)。
H = np.hstack((np.zeros(200), np.arange(100)/100, np.zeros(200)))
w = np.linspace(-0.5, 0.5, 500)
plt.plot(w, H, '.-')
plt.show()
# (剩下代码同上文示例)
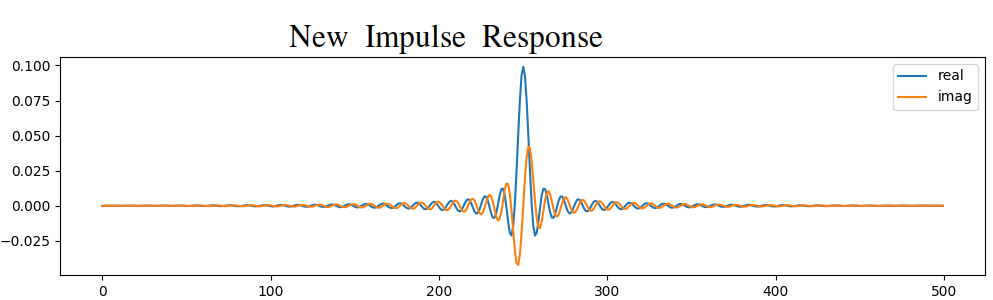
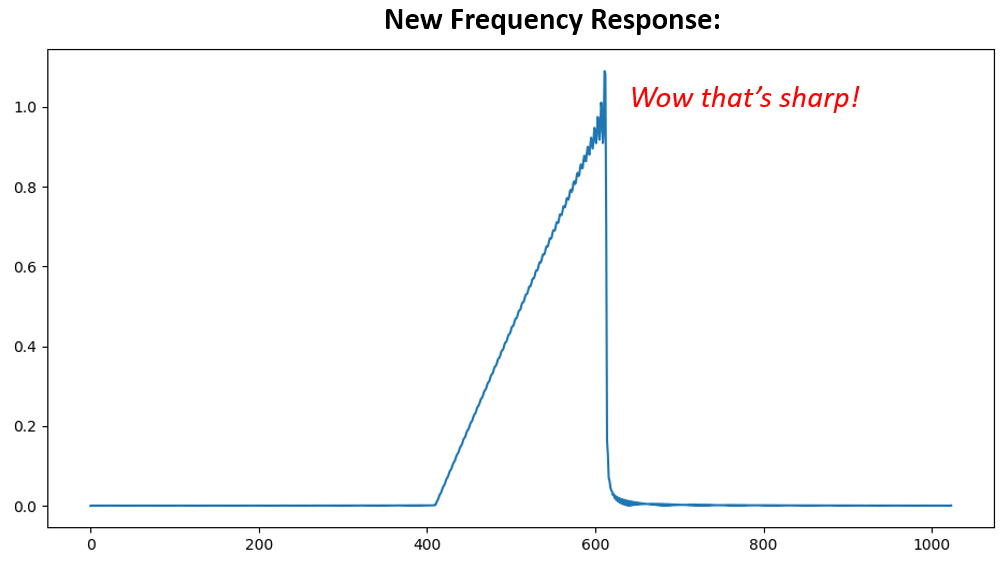
两种方法都可行。你会选择哪一种?第二种方法产生了更多的抽头,但第一种方法产生的频率响应不是很尖锐,下降沿也不是很陡峭。可见,设计滤波器的方法有很多,每种方法都有自己的取舍。许多人认为滤波器设计是一门艺术。
脉冲整形简介¶
我们将简要介绍数字信号处理中一个非常有趣的主题 — 脉冲整形。后面还有专门的章节会深入探讨这一主题,请参见 pulse-shaping-chapter 。在滤波器的部分要提一下脉冲整形,是因为它归根结底是一种滤波器,用于特定目的、具有特殊属性的滤波器。
前面我们讲到过,数字信号使用符号来表示一个或多个比特的信息。 我们使用 ASK、PSK、QAM、FSK 等数字调制方案对载波进行调制,从而以无线方式发送信息。 当我们在 数字调制 一章中模拟 QPSK 时,我们只模拟了每个符号对应一个采样的情况,也就是说,我们创建的每个复数就是星座上的一个点 — 它就是一个符号。 实际上,我们通常会为每个符号生成多个采样,原因就与滤波有关。
我们使用滤波器来修整符号的 “形状”,因为改变时域的形状也就改变了频域的形状。 信号在频域的形状告诉我们信号将使用多少频谱/带宽,我们通常希望将其最小化。 需要理解的是,当我们对载波进行调制时,基带符号的频谱特性(频域)并不会改变;它只是将基带的频率上移,而形状保持不变,这意味着它使用的带宽保持不变。 当我们使用每个符号 1 个采样点时,就像是在传输方形脉冲。 事实上,使用每个符号 1 个采样的 BPSK 只是一个 1 和 -1 随机出现的方波:
正如我们已经了解到的,方形脉冲的效率不高,因为它们占用了过量的频谱:
因此,我们要做的就是对这些块状符号进行 “脉冲整形”,以减少它们在频域中所占的带宽。我们使用低通滤波器进行 “脉冲整形”,因为它能剔除符号中的高频成分。 下图显示了在应用脉冲整形滤波器之前和之后,符号在时域(上)和频域(下)中的样子:
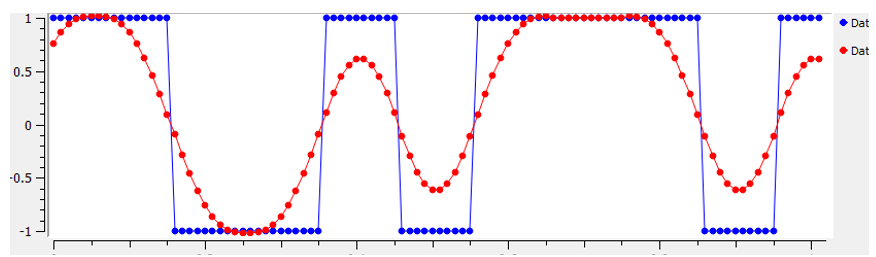
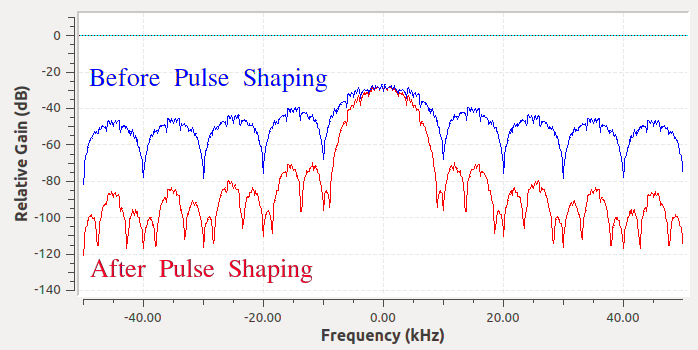
请注意看一些频率上的信号能量下降的有多快。脉冲整形后,边带降低了约 30 dB,相当于降低了 1000 倍!更重要的是,主频带更窄了,因此每秒相同比特数信息使用的频谱更少了。
目前,常见的脉冲整形滤波器包括
- 升余弦滤波器
- 根升余弦滤波器
- Sinc 滤波器
- 高斯滤波器
这些滤波器一般都有一个参数,调整它可以减小所使用的带宽。下图展示了升余弦滤波器在时域和频域的形状,当 \(\beta\) 取不同值的时候,改变了滚降的陡峭程度。
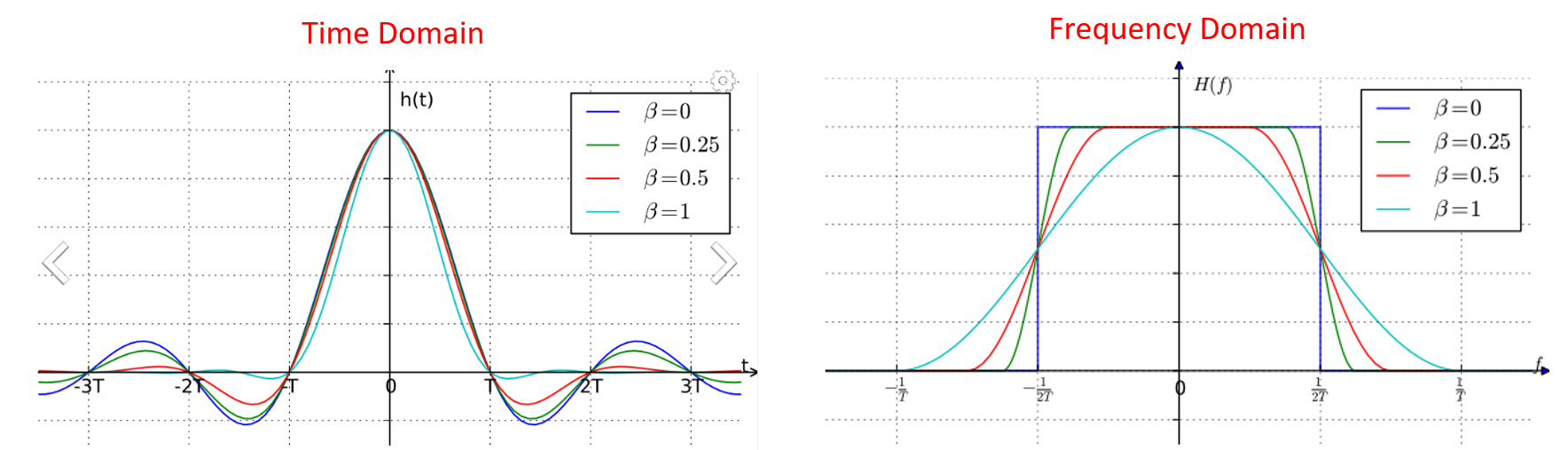
可以看到,\(\beta\) 的值越小(对于相同的数据量),使用的频谱就越少。但是,如果该值太低,时域符号衰减为零的时间会更长。实际上,当 \(\beta=0\) 时,符号永远不会完全衰减为零,这意味着我们实际上无法传输这样的符号。常用的 \(\beta\) 值为 0.35 左右。
你将在 pulse-shaping-chapter 章节了解到更多有关脉冲整形的信息,包括脉冲整形滤波器必须满足的一些特殊属性。