11. Канальне кодування

У цьому розділі ми ознайомимось з основами кодування каналу, таким як пряма корекція помилок під час передачі (FEC), межі Шеннона, кодами Хеммінга, Турбо-кодами та LDPC-кодами. Кодування каналу — це величезна галузь бездротових комунікацій та галузь “теорії інформації”, яка вивчає кількісну оцінку, зберігання та передачу інформації.

Для чого потрібне канальне кодування

Як ми вже дізналися Шум і дБ з розділу про шуми, у бездротових каналів є шумни, і наші цифрові символи досягають приймача в спотвореному стані. Якщо ви проходили курс з мережевих технологій, ви, можливо, вже знаєте про перевірку циклічним надлишковим кодом (CRC), яка виявляє помилки при прийомі. Мета кодування каналу полягає у виявленні і виправлені помилок на бочі приймача. Якщо дозволено певний рівень помилок, то наприклад можно передавати дані за допомогою модуляції вищого порядку, не маючи перерв у зв’язку. Як приклад розгляньте наступні зображення констеляції, QPSK (ліворуч) та 16QAM (праворуч) з однаковим рівнем шуму. QPSK забезпечує 2 біти на символ, тоді як 16QAM має вдвічі більшу швидкість передачі даних при 4 бітах на символ. Але зверніть увагу на те, як що QPSK символи у констеляції, як правило, не перетинають межу розрізнення символів, або вісі x, y, що означає, що символи будуть прийняті приймачем правильно. Тим часом на графіку 16QAM є перекриття кластерів, і, як наслідок, буде багато неправильно прийнятих символів.

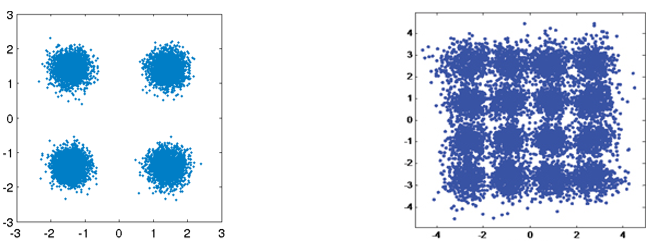
Невдала перевірка CRC зазвичай призводить до повторної передачі, принаймні при використанні протоколу, як-от TCP. Якщо Аліса надсилає повідомлення Бобу, ми б воліли, щоб Бобу не доводилося надсилати повідомлення назад Алісі з проханням повторно надіслати інформацію. Метою кодування каналу є передача надлишкової інформації. Надлишковість є запобіжником, який зменшує кількість помилкових пакетів, повторних передач або втрачених даних.

Ми обговорили, чому нам потрібне кодування каналу, тому давайте подивимося, де воно застосовується в ланцюжку передачі-прийому:

Зверніть увагу, що в ланцюжку передачі-прийому є декілька етапів кодування. Кодування джерела, наш перший крок, не те саме, що і кодування каналу; кодування джерела призначене для максимального стиснення даних, які потрібно передати, так само, як коли ви архівуєте файли, щоб зменшити простір, що вони займають. Тобто вихідний сигнал блоку кодування джерела повинен бути меншим , ніж вхідні дані, але вихідний сигнал канального кодування буде більшим за його вхід, оскільки додається надлишковість.

Типи Кодів

Для канального кодування ми використовуємо “код корекції помилок”. Цей код показує нам, які саме біти ми маємо передавати з урахуванням тих бітів, які нам потрібно передати. Найпростіший код називається “кодуванням повторення”, і він полягає в тому, що біт просто повторюється N разів поспіль. Для коду повторення-3 кожен біт передається тричі:

• 0 → 000

• 1 → 111

Повідомлення 10010110 передається як 111000000111000111111000 після канального кодування.

Деякі коди працюють з “блоками” вхідних бітів, а інші з “потоком” бітів. Коди, що працюють з блоками, даних певної довжини, називаються “Блоковими кодами”, тоді як коди, що працюють з потоком бітів, де довжина даних є довільною, називаються “згортоквими кодами”. Це два основні типи кодів. Наш код повторення-3 є блоковим кодом, де кожен блок складається з трьох бітів.

До речі, ці коди корекції помилок не використовуються виключно при кодуванні бездротових каналів зв’язку. Коли ви зберігаєте інформацію на жорсткий диск або SSD, вам не доводилося замислюватися, чому при зчитуванні інформації ніколи не виникає бітових помилок? Запис та зчитування з пам’яті подібні до системи зв’язку. Контролери жорстких/SSD дисків мають вбудовану корекцію помилок. Така корекція прозора для операційної системи і її алгоритм може бути пропрієтарним, оскільки вбудован безпосередньо в жорсткий диск/SSD. Для портативних носіїв, таких як компакт-диски, корекція помилок повинна бути стандартизованою. Зазвичай коди Ріда-Соломона використовуються в CD-ROM.

Коефіцієнт Кодування

Усі методи корекції помилок містять деяку форму надлишковості. Це означає, що якщо ми хочемо передати 100 бітів інформації, нам насправді доведеться відправити більше ніж 100 бітів. “Коефіцієнт кодування” – це співвідношення кількості інформаційних бітів до загальної кількості відправлених бітів (тобто інформаційних плюс надлишкових бітів). Повертаючись до прикладу кодування з трьома повтореннями, якщо у мене є 100 бітів інформації, то ми можемо визначити наступне:

• 300 бітів відправляються

• Тільки 100 бітів представляють інформацію

• Коефіцієнт кодування = 100/300 = 1/3

Коефіцієнт кодування завжди буде меншим за 1, оскільки це компроміс між надлишковістю та пропускною здатністю. Нижча швидкість коду означає більшу надлишковість і меншу пропускну здатність.

Модуляція та Кодування

У розділі Цифрова модуляція ми розглядали вплив шуму при різних схемах модуляції. При низькому співвідношенні сигнал/шум (SNR) вам потрібно використовувати модуляцію нижчого порядку (наприклад, QPSK) для того, щоб впоратися з шумом, а при високому рівні сигнад/шум (SNR) можна використовувати модуляцію, таку як 256QAM, для отримання більшої кількості бітів за секунду. Канальне кодування працює за аналогічним принципом; ми хочетмо мати нижчі коефіцієнти кодування при низьких значенях с/ш (SNR) та коефіцієнт кодування майже рівний 1 при високих значеннях с/ш (SNR). Сучасні комунікаційні системи мають набір комбінації схем модуляції та кодування, які називаються модуляціно-кодувальна схема МКС (MCS Modulation and Coding Scheme). Кожен МКС (MCS) визначає схему модуляції та кодування, які повинні використовуватися при певних рівнях с/ш (SNR).

Сучасні комунікації адаптивно змінюють МКС (MCS) в реальному часі відповідно умов бездротового каналу. Приймач надає зворотний зв’язок про якість каналу передавачу. Зворотній зв’язок повинен бути отриман до того як відбудуться зміни якості каналу, що може відповідати інтервалу часу порядка мілісекунд. Цей адаптивний процес призводить до максимально можливої пропускної здатності швидкості передачі даних та використовується в сучасних технологіях, таких як LTE, 5G та WiFi. Нижче зображено як змінює МКС (MCS) базова станція під час передачі залежно від відстані до користувача.

При використані адаптивної МКС (MCS), графіка залежності пропускної здатності від с/ш (SNR) буде у формі сходинок, як показано нижче. Протоколи, такі як LTE, часто мають таблицю, яка вказує, який МКС (MCS) слід використовувати при якому SNR.

Код Хеммінга

Давайте розглянемо прості коди корекції помилок. Код Хеммінга був першим розробленим нетрівіальнми кодом. В кінці 1940-х років Річард Хеммінг працював в лабораторії Bell, використовуючи електромеханічний комп’ютер на перфокартках. Коли в машині виявлялися помилки, вона зупинялася, і операторам доводилося їх виправляти. Хеммінг був розчарований необхідністю перезапускати свої програми заново через виявлені помилки. Він казав: “Чорт візьми, якщо машина може виявити помилку, чому вона не може визначити положення помилки і виправити її?” Наступні кілька років він розробляв код Хеммінга, щоб комп’ютер міг робити саме це.

У кодах Хеммінга додаткові біти, які називаються бітами парності або контрольними бітами, додаються до інформації для забезпечення надлишковості. Всі позиції бітів, які є ступенями двійки, є бітами парності: 1, 2, 4, 8 тощо. Інші позиції бітів призначені для інформації. В таблиці під цим абзацом біти парності виділені зеленим кольором. Кожен біт парності розраховується з всіх бітів, у яких операція побітового І (AND) позиції біта парності і позиції біта даних не є нульовим, ці позиції для різних бітів парності позначені червоним Х, дивись нижче. Якщо ми хочемо використовувати біт даних, нам потрібні біти парності, які його покривають. Тобто щоб мати можливість використовувати біт даних d9, нам буде потрібен біт парності p8 та всі попередні біти парності. Отже, ця таблиця підказує нам, скільки бітів парності нам потрібно для певної кількості бітів. Цей шаблон при необхідності більшой кількості бітів даних можно продовжувати нескінченно.

Коди Хеммінга є блоковими кодами, тому вони працюють по N бітів даних за раз. Таким чином в одному блоці, три біти парності дають можливість мати у блоках чотири біта даних. Цю схему кодування від помилок представляємо як Hamming(7,4), де перший аргумент — це загальна кількість переданих бітів (біти парності + біти даних), а другий аргумент — це кількість бітів даних.

Наступні три важливі властивості кодів Хеммінга (код, кодове слово - це блок для певних даних та вирохованих бітів парності, що стоять на певних місцях):

• Мінімальна кількість змін бітів, необхідних для переходу від одного кодового слова до іншого, становить три

• Код Хеммінга може виправляти однобітові помилки. (При помилці, розрахунок бітов парності вкаже на позицію де відбулась помилка. При цьому неважливо був це біт парності, чи даних)

• Код Хеммінга може виявляти, але не виправляти двобітові помилки

Алгоритмічно процес кодування можна здійснити за допомогою простого множення матриць, використовуючи так звану “матрицю генератора”. У наведеному нижче прикладі вектор 1011 є даними (інформацією), які потрібно закодувати і яку ми хочемо надіслати отримувачу. 2D-матриця називається матрицею генератора, і визначає схему кодування. Результат множення дає кодове слово для передачі.

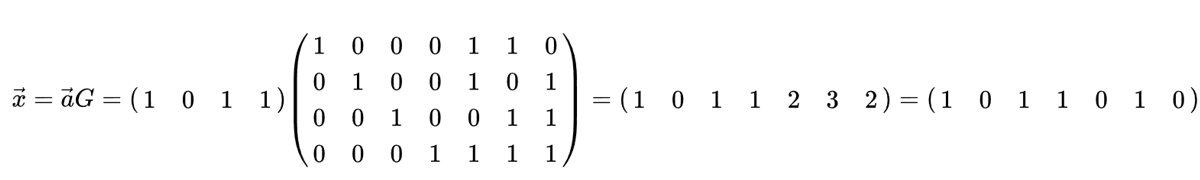
Мета “занурення” в коди Хеммінга полягає в тому, щоб дати уявлення про те, як працює кодування для корекції помилок. Блокові коди, як правило, відповідають цьому типу схеми кодування. Згорткові коди працюють інакше, але зараз заглиблюватися в це ми не будемо; вони часто використовують декодування по схемі Трелліса, яке зображено на рисунку нижче:

(Порівняння м’якого та жорсткого декодування) Soft vs Hard Decoding

Ви пам’ятаєте, що в приймачі демодуляція відбувається перед декодуванням. Демодулятор може надати нам найкраще припущення щодо того, який символ був переданий, або може надати “м’яке” значення. Наприклад, для BPSK, замість того, щоб надати 1 або 0, демодулятор може надати 0.3423 або -1.1234, що є “м’яким” значенням символу. Зазвичай декодування розроблене для використання м’яких або жорстких значень.

• Декодування з м’яким рішенням (Soft decision decoding) – використовує м’які значення

• Декодування з жорстким рішенням (Наrd decision decoding) – використовує лише 1 та 0

М’яке декодування є більш надійним, оскільки ви використовуєте всю доступну інформацію, але м’яке декодування також значно складніше впровадити. Коди Хеммінга, про які ми говорили, використовувують декодування з жорстким рішенням, тоді як згорткові коди в більшості використовувують декодування з м’яким рішенням.

Границя Шеннона

Границя Шеннона або пропускна здатність по Шеннону - це неймовірний висновк з теорії, який дає нам розрахувати скільки бітів за секунду інформації без помилок ми можемо передати:

• C – Ємність каналу [біти/сек]

• B – Ширина смуги каналу [Гц]

• S – Середня потужність отриманого сигналу [Вати]

• N – Середня потужність шуму [Вати]

Ця рівняння представляє максимальне теоритичне значення, яке може представити певна система модуляції сигналу при достатньо високому значенні с/ш (SNR) для безпомилкової роботи. Логічніше представити границю в бітах/сек/Гц, тобто в бітах на секунду на певну частину спектра:

де сш (SNR) виражений в разах (не в децибелах). Проте, на графіку нижче, ми представимо сш (SNR) у дБ для зручності:

Якщо ви побачите десь графік границі Шеннона, що виглядає трохи інакше, то, ймовірно, по осі х відкладається “енергія на біт” або :math:E_b/N_0, що є просто альтернативою формою значенню сш (SNR).

Для розуміння, коли сш (SNR) досить високий (наприклад, 10 дБ або має більше значення), границю Шеннона може бути наближено приведено як , що приблизно дорівнює (пояснено тут). Наприклад, при значені сш (SNR) 24 дБ ви отримуєте близько 8 біт/сек/Гц, тож якщо у вас є смуга в 1 МГц для використання, це відповідає швидкості передачі 8 Мбіт/с. Можно подумати, що це лише теоретична границя, але у сучасному зв’язку реальні значення досить близькі до цієї границі, тому як мінімум це дає вам приблизну оцінку пропускної здатності. Завжди можете поділити це число навпіл, щоб врахувати накладні витрати на пакети/кадри і або неідеальність МКС (MCS).

Максимальна пропускна здатність WiFi 802.11n в діапазоні 2,4 ГГц (яка використовує канали шириною 20 МГц) за специфікацію становить 300 Мбіт/с. Звичайно, ви можете сидіти поруч з маршрутизатором і отримати дуже високе значення сш (SNR), і може дорівнювати 60 дБ, але для отримання надійних/реальних значень максимальної пропускної здатністі для певної МКС (MCS) (згадайте криву залежності пропускної здатності від значення с/ш у вигляді сходинок, наведену вище) малоймовірно, що вимагатимесь таке велике значення с/ш (SNR), що дорівнює 60 дБ. Можете навіть переглянути список МКС (MCS) для 802.11n <https://en.wikipedia.org/wiki/IEEE_802.11n-2009#Data_rates>. 802.11n підтримує до 64-QAM, і в поєднанні з кодуванням каналу вимагає с/ш (SNR) близько 25 дБ за цією таблицею <https://d2cpnw0u24fjm4.cloudfront.net/wp-content/uploads/802.11n-and-802.11ac-MCS-SNR-and-RSSI.pdf>. Це означає, що навіть при с/ш (SNR) 60 дБ ваш WiFi все ще буде використовувати 64-QAM. Таким чином, при 25 дБ границя Шеннона приблизно становить 8,3 біт/с/Гц, що при 20 МГц спектру дорівнює 166 Мбіт/с. Однак, якщо врахувати MIMO, яке ми розглянемо в майбутньому розділі, ви можете отримати чотири таких паралельних потоки, що дасть 664 Мбіт/с. Якщо це число поділити навпіл, ви отримаєте значення, дуже близьке до заявленої максимальної швидкості 300 Мбіт/с для WiFi 802.11n в діапазоні 2,4 ГГц.

Доведення границі Шеннона, досить складне; воно включає наступну математику:

Додаткову інформаціб дивись тут.

Найсучасніші коди

Наразі найкращі схеми кодування каналів:

1. Турбо-коди, що використовуються в 3G, 4G, космічних апаратах NASA.

2. LDPC-коди, що використовуються в DVB-S2, WiMAX, IEEE 802.11n.

Обидва ці коди наближаються до границі Шеннона (тобто майже досягають її при певних значеннях с/ш (SNR)). Коди Хеммінга та інші простіші коди не наближаються до границі Шеннона. З точки зору нових досліджень, залишилося небагато можливостей для покращення самих кодів. Поточні дослідження більше зосереджені на підвищенні обчислювальної ефективності декодування та адаптації до зворотного зв’язку по якості каналу.

Коди з низькою щільністю перевірки парності (LDPC) є класом високоефективних лінійних блокових кодів. Вони були вперше представлені Робертом Г. Галлаґером у його докторській дисертації в 1960 році в MIT. Через обчислювальну складність їх реалізації, ці коди ігнорувались до 1990-х років! На момент написання цього тексту (2020) винахідник цих кодів ще живий, йому 89 років, і він отримав багато нагород за свою роботу (через десятиліття після того, як він її винайшов). LDPC не патентовані і безкоштовні для використання (на відміну від турбо-кодів), що пояснює, чому вони використовувалися в багатьох відкритих протоколах.

Турбо-коди базуються на згорткових кодах. Це клас кодів, який поєднує два або більше простіших згорткових кодів та перемежувач. Основна патентна заявка на турбо-коди була подана 23 квітня 1991 року. Винахідники - французи, тому коли Qualcomm хотіла використовувати турбо-коди в CDMA для 3G, їм довелося створити платіжну патентну ліцензійну угоду з France Telecom. Основний патент закінчився 29 серпня 2013 року.