15. Синхронізація

У цьому розділі розглядається синхронізація бездротового сигналу в часі і частоті, щоб виправити зміщення несучої частоти і виконати вирівнювання часу на рівні символів і кадрів. Ми будемо використовувати техніку відновлення тактової частоти Мюллера і Мюллера, а також цикл Костаса в Python.

Вступ

Ми обговорили, як здійснювати цифрову передачу в ефірі, використовуючи схему цифрової модуляції, таку як QPSK, і застосовуючи формування імпульсів для обмеження смуги пропускання сигналу. Канальне кодування можна використовувати для роботи із зашумленими каналами, наприклад, коли у вас низький SNR на приймачі. Завжди корисно відфільтрувати якомога більше перед цифровою обробкою сигналу. У цьому розділі ми розглянемо, як виконується синхронізація на приймальному боці. Синхронізація - це набір операцій, які відбуваються перед демодуляцією і декодуванням каналу. Нижче показано загальний ланцюжок tx-канал-rx, де жовтим кольором виділено блоки, що розглядаються в цій главі. (Ця схема не є всеохоплюючою - більшість систем також включають еквалізацію і мультиплексування).

Моделювання бездротового каналу

Перш ніж ми навчимося реалізовувати часову та частотну синхронізацію, нам потрібно зробити наші імітовані сигнали більш реалістичними. Без додавання випадкової часової затримки, акт синхронізації в часі є тривіальним. Насправді, вам потрібно лише врахувати затримку дискретизації будь-яких фільтрів, які ви використовуєте. Ми також хочемо змоделювати зміщення частоти, тому що, як ми будемо обговорювати, генератори не є ідеальними; завжди буде деякий зсув між центральною частотою передавача і приймача.

Розглянемо код на Python для моделювання нецілочисельної затримки та зсуву частоти. Код на Python у цій главі почнеться з коду, який ми написали під час вправи з формування імпульсів на Python (натисніть нижче, якщо він вам потрібен); ви можете вважати його відправною точкою коду в цій главі, а весь новий код буде додано після неї.

Пітон-код з Pulse Shaping

import numpy as np
import matplotlib.pyplot as plt
з scipy import signal
import math

# ця частина прийшла з вправи на формування пульсу
num_symbols = 100
sps = 8
bits = np.random.randint(0, 2, num_symbols) # Наші дані для передачі, 1 та 0
pulse_train = np.array([])
для біта в бітах:
    pulse = np.zeros(sps)
    pulse[0] = bit*2-1 # встановлюємо перше значення в 1 або -1
    pulse_train = np.concatenate((pulse_train, pulse)) # додаємо 8 відліків до сигналу

# створюємо наш фільтр підвищеної косинусоїди
num_taps = 101
beta = 0.35
Ts = sps # Припустимо, що частота дискретизації 1 Гц, період дискретизації 1, період *символу* 8
t = np.arange(-51, 52) # пам'ятайте, що це не включно з кінцевим числом
h = np.sinc(t/Ts) * np.cos(np.pi*beta*t/Ts) / (1 - (2*beta*t/Ts)**2)

# Фільтруємо наш сигнал, щоб застосувати формування імпульсів
samples = np.convolve(pulse_train, h)

Ми пропустимо код, пов’язаний з побудовою графіків, оскільки ви вже навчилися будувати графіки будь-яких сигналів. Надання графікам красивого вигляду, як це часто робиться у цьому підручнику, вимагає багато додаткового коду, який не обов’язково розуміти.

Додавання затримки

Ми можемо легко імітувати затримку, зсуваючи відліки, але це імітує лише затримку, яка є цілим числом, кратним періоду нашого відліку. У реальному світі затримка буде становити деяку частку від періоду зразка. Ми можемо імітувати затримку на частку відрізка, створивши фільтр “дробової затримки”, який пропускає всі частоти, але затримує відрізки на деяку величину, яка не обмежується інтервалом відрізка. Ви можете думати про це як про багатосмуговий фільтр, який застосовує однаковий фазовий зсув до всіх частот. (Нагадаємо, що часова затримка і фазовий зсув еквівалентні.) Код на Python для створення цього фільтра наведено нижче:

# Створити і застосувати фільтр дробової затримки
delay = 0.4 # дробова затримка, у відліках
N = 21 # кількість відведень
n = np.arange(-N/2, N//2) # ...-3,-2,-1,0,1,2,3...
h = np.sinc(n - delay) # обчислюємо відгалуження фільтру
h *= np.hamming(N) # вікно фільтра, щоб переконатися, що він розпадається до 0 з обох боків
h /= np.sum(h) # нормалізуємо, щоб отримати одиничний коефіцієнт підсилення, ми не хочемо змінювати амплітуду/потужність
samples = np.convolve(samples, h) # застосовуємо фільтр

Як бачите, ми обчислюємо відводи фільтра за допомогою функції sinc(). Sinc у часовій області - це прямокутник у частотній області, і наш прямокутник для цього фільтра охоплює весь частотний діапазон нашого сигналу. Цей фільтр не змінює форму сигналу, він лише затримує його в часі. У нашому прикладі ми затримуємо на 0,4 відрізка. Майте на увазі, що застосування будь-якого фільтра затримує сигнал на половину відліків фільтра мінус один, через акт згортки сигналу через фільтр.

Якщо ми побудуємо графік “до” і “після” фільтрації сигналу, то зможемо побачити дробову затримку. На нашому графіку ми збільшили масштаб лише на кілька символів. Інакше дробову затримку не видно.

Додавання частотного зсуву

Щоб зробити наш імітований сигнал більш реалістичним, ми застосуємо частотний зсув. Скажімо, наша частота дискретизації в цій симуляції становить 1 МГц (насправді не має значення, якою вона буде, але ви побачите, чому це полегшує вибір числа). Якщо ми хочемо змоделювати зсув частоти на 13 кГц (якесь довільне число), ми можемо зробити це за допомогою наступного коду:

# застосовуємо зсув частоти
fs = 1e6 # вважаємо, що наша частота дискретизації дорівнює 1 МГц
fo = 13000 # імітуємо зсув частоти
Ts = 1/fs # обчислюємо період дискретизації
t = np.arange(0, Ts*len(samples), Ts) # створюємо вектор часу
samples = samples * np.exp(1j*2*np.pi*fo*t) # виконуємо зсув частоти

Нижче демонструється сигнал до і після застосування зсуву частоти.

Ми не будували графік Q-частини, оскільки передавали BPSK, і тому Q-частина завжди дорівнювала нулю. Тепер, коли ми додаємо частотний зсув для імітації бездротових каналів, енергія розподіляється між I і Q. З цього моменту ми повинні будувати графіки як I, так і Q. Не соромтеся підставляти інший частотний зсув для вашого коду. Якщо ви зменшите зсув приблизно до 1 кГц, ви зможете побачити синусоїду в огинаючій сигналу, оскільки вона коливається досить повільно, щоб охопити кілька символів.

Що стосується вибору довільної частоти дискретизації, то якщо ви уважно подивитеся на код, то помітите, що важливим є співвідношення fo до fs.

Можна уявити, що два блоки коду, представлені раніше, імітують бездротовий канал. Код повинен стояти після коду на стороні передачі (що ми робили у розділі про формування імпульсів) і перед кодом на стороні прийому, який ми розглянемо у решті частини цього розділу.

Синхронізація часу

Коли ми передаємо сигнал бездротовим способом, він надходить до приймача з випадковим фазовим зсувом через пройдений час. Ми не можемо просто почати вибірку символів з нашою швидкістю, тому що ми навряд чи зможемо зробити вибірку у потрібній точці імпульсу, як це обговорюється у кінці розділу Pulse Shaping. Якщо ви не зрозуміли, перегляньте три рисунки в кінці цього розділу.

Більшість методів синхронізації мають форму петлі фазової автопідстроювання (ФАПЧ); ми не розглядатимемо ФАПЧ тут, але важливо знати цей термін, і ви можете почитати про них самостійно, якщо вам цікаво. ФАПЧ - це замкнені системи, які використовують зворотний зв’язок для постійного коригування чогось; у нашому випадку зсув у часі дозволяє нам робити вибірки на піку цифрових символів.

Ви можете уявити відновлення синхронізації як блок в приймачі, який приймає потік відліків і видає інший потік відліків (подібно до фільтра). Ми програмуємо цей блок відновлення синхронізації інформацією про наш сигнал, найважливішою з яких є кількість відліків на символ (або наше найкраще припущення, якщо ми не впевнені на 100%, що було передано). Цей блок діє як “дециматор”, тобто наша вихідна вибірка буде часткою від кількості вхідних відліків. Нам потрібен один відлік на цифровий символ, тому частота децимації - це просто кількість відліків на символ. Якщо передавач передає зі швидкістю 1 млн. символів на секунду, а ми робимо дискретизацію зі швидкістю 16 Мс, то отримаємо 16 відліків на символ. Це буде частота дискретизації, що надходить у блок синхронізації. Частота дискретизації на виході з блоку буде 1 Msps, тому що нам потрібна одна вибірка на цифровий символ.

Більшість методів відновлення синхронізації ґрунтуються на тому, що наші цифрові символи піднімаються, а потім опускаються, і вершина - це точка, в якій ми хочемо зробити вибірку символу. Іншими словами, ми робимо вибірку в максимальній точці після зняття абсолютного значення:

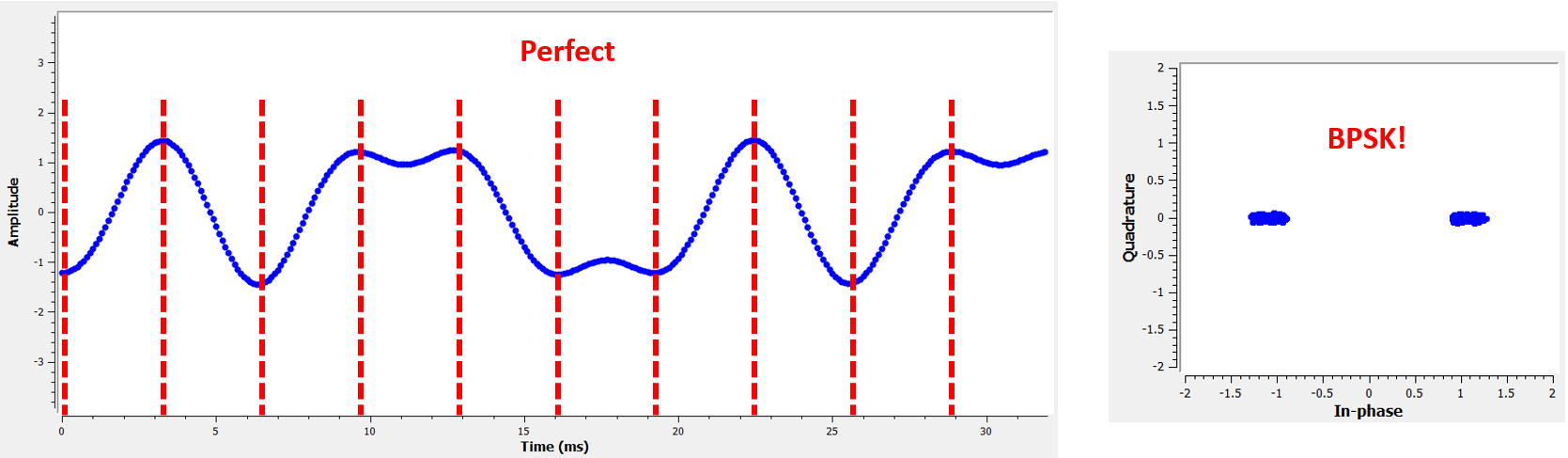
Існує багато методів відновлення синхронізації, які здебільшого нагадують ШІМ. Різниця між ними полягає у рівнянні, яке використовується для виконання “корекції” зсуву синхронізації, яке ми позначаємо як або mu у коді. Значення mu оновлюється на кожній ітерації циклу. Це значення в одиницях відліків, і ви можете думати про нього як про те, на скільки ми повинні зміститися, щоб мати змогу зробити вибірку в “ідеальний” момент часу. Отже, якщо mu = 3.61, це означає, що нам потрібно зсунути вхідні дані на 3.61 відліки, щоб зробити вибірку в потрібному місці. Оскільки ми маємо 8 відліків на символ, якщо mu перевищить 8, він просто повернеться до нуля.

Наступний код на Python реалізує техніку Мюллера і відновлення тактового генератора Мюллера.

mu = 0 # початкова оцінка фази зразка
out = np.zeros(len(samples) + 10, dtype=np.complex)
out_rail = np.zeros(len(samples) + 10, dtype=np.complex) # зберігає значення, на кожній ітерації нам потрібні 2 попередні значення плюс поточне значення
i_in = 0 # індекс вхідних відліків
i_out = 2 # індекс виходу (нехай перші два виходи дорівнюють 0)
while i_out < len(samples) and i_in+16 < len(samples):
    out[i_out] = samples[i_in + int(mu)] # беремо те, що вважаємо "найкращим" зразком
    out_rail[i_out] = int(np.real(out[i_out]) > 0) + 1j*int(np.imag(out[i_out]) > 0)
    x = (out_rail[i_out] - out_rail[i_out-2]) * np.conj(out[i_out-1])
    y = (out[i_out] - out[i_out-2]) * np.conj(out_rail[i_out-1])
    mm_val = np.real(y - x)
    mu += sps + 0.3*mm_val
    i_in += int(np.floor(mu)) # округляємо до найближчого int, оскільки використовуємо його як індекс
    mu = mu - np.floor(mu) # видаляємо цілу частину mu
    i_out += 1 # збільшити індекс виводу
out = out[2:i_out] # видаляємо перші два рядки і все, що після i_out (що ніколи не заповнювалось)
samples = out # включайте цей рядок лише у тому випадку, якщо ви хочете пізніше з'єднати цей фрагмент коду з циклом Костаса

На блок відновлення синхронізації подаються “отримані” відліки, і він видає вихідний відлік по одному за раз (зверніть увагу на те, що i_out збільшується на 1 на кожній ітерації циклу). Блок відновлення не просто використовує “отримані” зразки один за одним, тому що цикл коригує i_in. Він пропускає деякі відліки, намагаючись витягнути “правильний” відлік, тобто той, що знаходиться на піку імпульсу. Коли цикл обробляє відліки, він повільно синхронізується з символом, або, принаймні, намагається це зробити, змінюючи mu. Враховуючи структуру коду, ціла частина mu додається до i_in, а потім вилучається з mu (майте на увазі, що mm_val може бути від’ємною або додатною кожного циклу). Після повної синхронізації цикл має витягувати лише центральний відлік з кожного символу/імпульсу. Ви можете налаштувати константу 0.3, яка змінює швидкість реакції циклу зворотного зв’язку; більше значення робить його реакцію швидшою, але з більшим ризиком проблем зі стабільністю.

На наступному графіку показано приклад вихідного сигналу, де ми відключили дробову затримку, а також зміщення частоти. Ми показуємо лише I, оскільки Q - це нулі, а частотний зсув вимкнено. Три графіки накладено один на одного, щоб показати, як біти вирівнюються по вертикалі.

Верхній графік

Оригінальні символи BPSK, тобто 1 і -1. Пам’ятайте, що між ними є нулі, тому що нам потрібно 8 вибірок на символ.

Середній графік

Відліки після формування імпульсів, але до синхронізатора.

Нижній графік

Вихід символьного синхронізатора, який забезпечує лише 1 вибірку на символ. Тобто ці відліки можна подавати безпосередньо на демодулятор, який для BPSK перевіряє, чи значення більше або менше 0.

Зосередимося на нижньому графіку, який є виходом синхронізатора. Знадобилося майже 30 символів, щоб синхронізація зафіксувалася з потрібною затримкою. Через неминучий час, необхідний для синхронізації, багато протоколів зв’язку використовують преамбулу, яка містить послідовність синхронізації: вона діє як спосіб повідомити про те, що прибув новий пакет, і дає приймачу час для синхронізації з ним. Але після цих ~30 семплів синхронізатор працює ідеально. У нас залишаються ідеальні 1 і -1, які відповідають вхідним даним. Допомагає те, що в цьому прикладі не було додано жодного шуму. Не соромтеся додавати шум або часові зсуви і подивіться, як поводитиметься синхронізатор. Якби ми використовували QPSK, то мали б справу з комплексними числами, але підхід був би таким самим.

Синхронізація часу за допомогою інтерполяції

Синхронізатори символів, як правило, інтерполюють вхідні відліки на деяке число, наприклад, 16, так що вони можуть зміщуватися на частку відліку. Випадкова затримка, спричинена бездротовим каналом, навряд чи буде точно кратною відліку, тому пік символу може не збігатися з відліком. Це особливо актуально у випадку, коли на один символ може припадати лише 2 або 4 відліки. Інтерполюючи відліки, він дає нам можливість робити відліки “між” реальними відліками, щоб потрапити на самий пік кожного символу. На виході синхронізатора залишається лише 1 відлік на символ. Самі вхідні відліки інтерполюються.

Наш код синхронізації часу на Python, який ми реалізували вище, не включав ніякої інтерполяції. Щоб розширити наш код, увімкніть дробову часову затримку, яку ми реалізували на початку цього розділу, щоб наш отриманий сигнал мав більш реалістичну затримку. Частотний зсув поки що залиште вимкненим. Якщо ви повторно запустите симуляцію, то побачите, що синхронізатор не може повністю синхронізуватися з сигналом. Це тому, що ми не інтерполюємо, тому код не має можливості “робити вибірку між вибірками”, щоб компенсувати дробову затримку. Давайте додамо інтерполяцію.

Швидкий спосіб інтерполювати сигнал у Python - скористатися функціями signal.resample або signal.resample_poly з пакета scipy. Ці функції роблять одне й те саме, але працюють по-різному. Ми будемо використовувати останню функцію, оскільки вона, як правило, швидша. Давайте інтерполюватимемо на 16 (це довільний вибір, ви можете спробувати різні значення), тобто ми будемо вставляти 15 додаткових відліків між кожним відліком. Це можна зробити в одному рядку коду, і це повинно відбутися до того, як ми підемо виконувати синхронізацію часу (до великого фрагмента коду вище). Давайте також побудуємо графік до і після, щоб побачити різницю:

samples_interpolated = signal.resample_poly(samples, 16, 1)

# Побудувати графік старого та нового
plt.figure('before interp')
plt.plot(samples,'.-')
plt.figure('after interp')
plt.plot(samples_interpolated, '.-')
plt.show()

Якщо ми збільшимо масштаб, то побачимо, що це той самий сигнал, тільки з 16x більшою кількістю точок:

Сподіваємось, причина, чому нам потрібно інтерполювати всередині блоку синхронізації часу, стає зрозумілою. Ці додаткові вибірки дозволять нам врахувати частку затримки вибірки. На додаток до обчислення samples_interpolated, нам також потрібно змінити один рядок коду в нашому синхронізаторі часу. Ми змінимо перший рядок всередині циклу while на become:

out[i_out] = samples_interpolated[i_in*16 + int(mu*16)]

Тут ми зробили кілька речей. По-перше, ми більше не можемо просто використовувати i_in як індекс вхідної вибірки. Ми повинні помножити його на 16, тому що ми інтерполювали наші вхідні відліки на 16. Пам’ятайте, що цикл зворотного зв’язку коригує змінну mu. Вона являє собою затримку, яка призводить до того, що ми робимо вибірку в потрібний момент. Також нагадаємо, що після обчислення нового значення mu ми додали цілу частину до i_in. Тепер ми будемо використовувати залишок, який є плаваючою частиною від 0 до 1, і представляє собою частку відрізка, на яку нам потрібно затримати дискретизацію. Раніше ми не могли затримати на частку відліку, але тепер ми можемо, принаймні з кроком у 16 частин відліку. Ми множимо mu на 16, щоб дізнатися, на скільки відліків нашого інтерпольованого сигналу нам потрібно затримати. А потім ми повинні округлити це число, оскільки значення в дужках є індексом і має бути цілим числом. Якщо цей абзац не має сенсу, спробуйте повернутися до початкового коду Мюллера і відновлення годинника Мюллера, а також прочитайте коментарі біля кожного рядка коду.

Фактичний вивід графіка цього нового коду має виглядати приблизно так само, як і раніше. Ми лише зробили нашу симуляцію більш реалістичною, додавши затримку дробової вибірки, а потім додали інтерполятор до синхронізатора, щоб компенсувати цю затримку дробової вибірки.

Не соромтеся експериментувати з різними коефіцієнтами інтерполяції, тобто змінюйте всі 16 с на інші значення. Ви також можете спробувати увімкнути частотний зсув або додати білий гаусівський шум до сигналу до того, як він буде отриманий, щоб побачити, як це впливає на якість синхронізації (підказка: можливо, вам доведеться відкоригувати множник 0.3).

Якщо ми увімкнемо лише зміщення частоти, використовуючи частоту 1 кГц, ми отримаємо такі показники часової синхронізації. Тепер, коли ми додали зсув частоти, нам потрібно показати і I, і Q:

Можливо, це важко помітити, але синхронізація часу все ще працює чудово. Потрібно приблизно 20-30 символів, щоб вона зафіксувалася. Однак, ми бачимо синусоїду, тому що у нас все ще є зсув частоти, і ми дізнаємося, як з ним впоратися в наступному розділі.

Нижче показано IQ-графік (так званий графік сузір’я) сигналу до і після синхронізації. Пам’ятайте, що ви можете нанести відліки на IQ-діаграму за допомогою діаграми розсіювання: plt.plot(np.real(samples), np.imag(samples), '.'). На анімації нижче ми спеціально пропустили перші 30 символів. Вони з’явилися до того, як закінчилася синхронізація часу. Всі символи, що залишилися, знаходяться приблизно на одиничному колі через зсув частоти.

Щоб отримати ще більше розуміння, ми можемо подивитися на сузір’я в часі, щоб побачити, що насправді відбувається з символами. На самому початку, протягом короткого проміжку часу, символи не дорівнюють 0 і не знаходяться на одиничному колі. Це період, коли синхронізація часу знаходить правильну затримку. Це відбувається дуже швидко, слідкуйте уважно! Обертання - це просто зсув частоти. Частота - це постійна зміна фази, тому зміщення частоти спричиняє обертання BPSK (створення кола на статичному/постійному графіку вище).

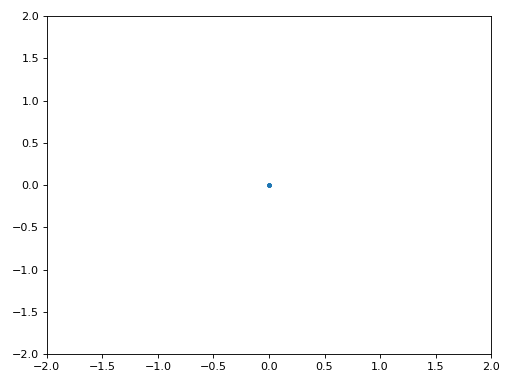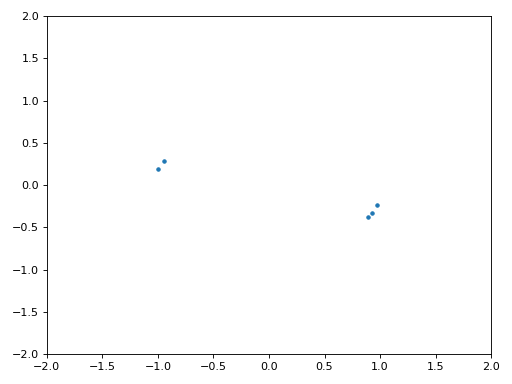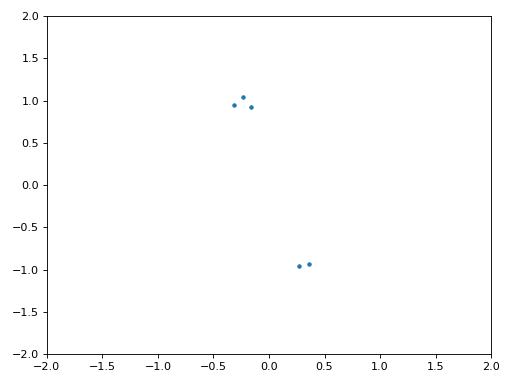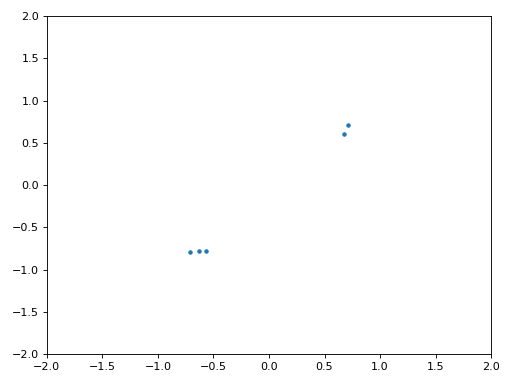
Сподіваюся, побачивши приклад реальної синхронізації часу, ви зрозуміли, що вона робить, і отримали загальне уявлення про те, як вона працює. На практиці, створений нами цикл while працюватиме лише з невеликою кількістю семплів за раз (наприклад, 1000). Ви повинні пам’ятати значення mu між викликами функції синхронізації, а також останні пару значень out і out_rail.

Далі ми розглянемо частотну синхронізацію, яку ми розділили на грубу і точну. Груба зазвичай відбувається перед синхронізацією, а точна - після.

Груба частотна синхронізація

Навіть якщо ми скажемо передавачу і приймачу працювати на одній центральній частоті, між ними буде невеликий зсув частоти через недосконалість обладнання (наприклад, генератора) або допплерівський зсув від руху. Цей зсув частоти буде крихітним відносно несучої частоти, але навіть невеликий зсув може призвести до спотворення цифрового сигналу. Зсув, ймовірно, змінюватиметься з часом, що вимагає постійного зворотного зв’язку для корекції зсуву. Наприклад, генератор всередині Плутона має максимальний зсув 25 PPM. Це 25 частин на мільйон відносно центральної частоти. Якщо ви налаштовані на 2,4 ГГц, максимальне зміщення становитиме +/- 60 кГц. Зразки, які нам надає SDR, знаходяться в базовій смузі частот, тому будь-яке зміщення частоти проявляється в цьому сигналі базової смуги. Сигнал BPSK з невеликим зсувом несучої буде виглядати приблизно так, як показано на часовій діаграмі нижче, що, очевидно, не дуже добре для демодуляції бітів. Перед демодуляцією ми повинні видалити будь-які частотні зсуви.

Частотну синхронізацію зазвичай поділяють на грубу та точну, де груба синхронізація виправляє великі зсуви порядку кГц або більше, а точна - все, що залишилося. Груба синхронізація відбувається до часової синхронізації, а точна - після.

Математично, якщо у нас є сигнал базової смуги і він зазнає частотного (так званого несучого) зсуву на Гц, ми можемо представити те, що отримуємо, як:

де - шум.

Перший трюк, якому ми навчимося, щоб виконати грубу оцінку частотного зсуву (якщо ми можемо оцінити частоту зсуву, то ми можемо його виправити), - це взяти квадрат нашого сигналу. Для спрощення обчислень проігноруємо шум:

Давайте подивимося, що станеться, коли ми піднесемо до квадрату наш сигнал , розглянувши, що зробить QPSK. Піднесення комплексних чисел до квадрата призводить до цікавої поведінки, особливо коли ми говоримо про такі сузір’я, як BPSK і QPSK. Наступна анімація показує, що відбувається, коли ви підносите QPSK до квадрата, а потім знову підносите до квадрата. Я спеціально використовував QPSK замість BPSK, тому що ви можете бачити, що коли ви підносите QPSK до квадрата один раз, ви по суті отримуєте BPSK. А потім після ще одного квадратування це стає одним кластером. (Дякуємо http://ventrella.com/ComplexSquaring/, який створив цей чудовий веб-додаток).

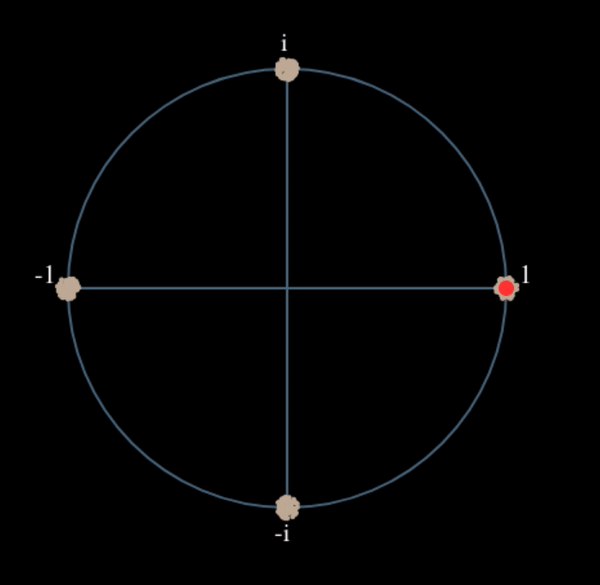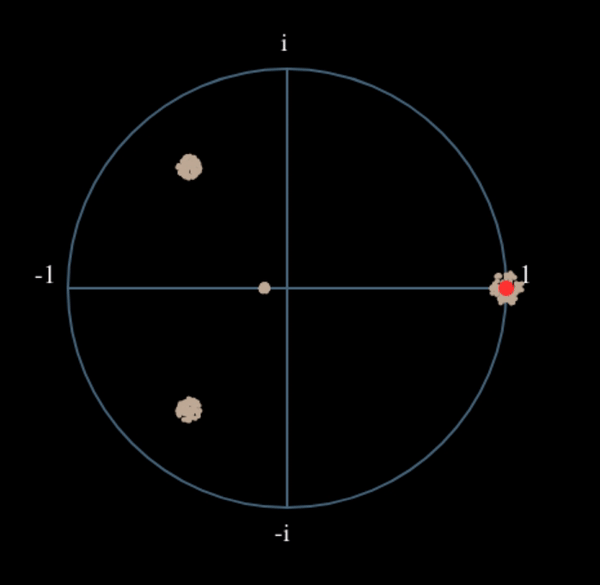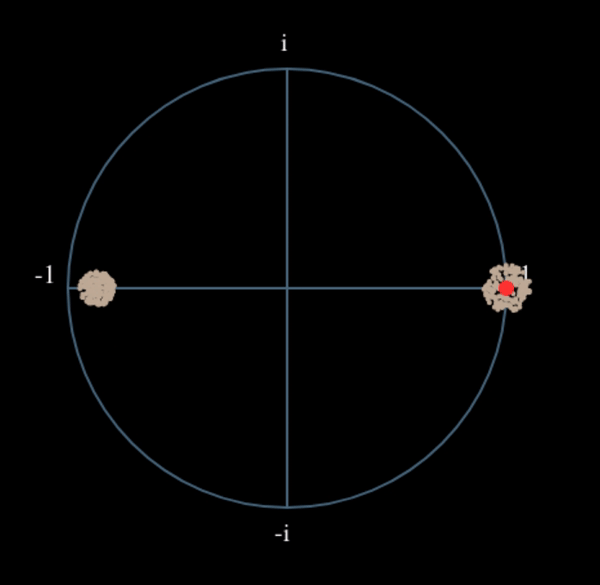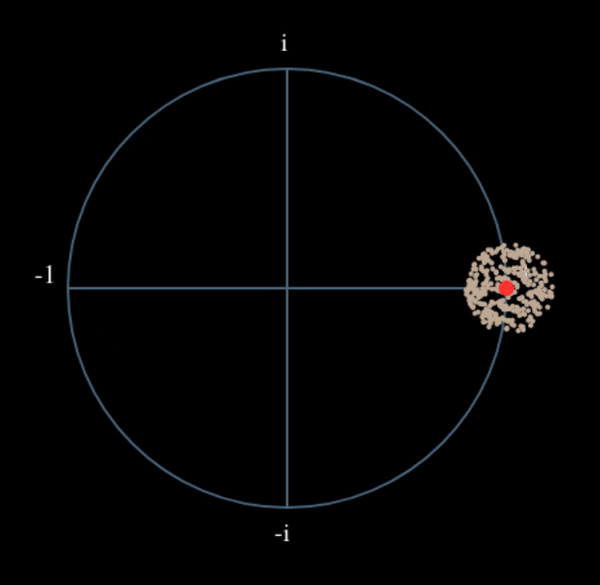
Давайте подивимося, що станеться, коли до нашого QPSK-сигналу застосувати невеликий поворот фази і масштабування амплітуди, що є більш реалістичним:

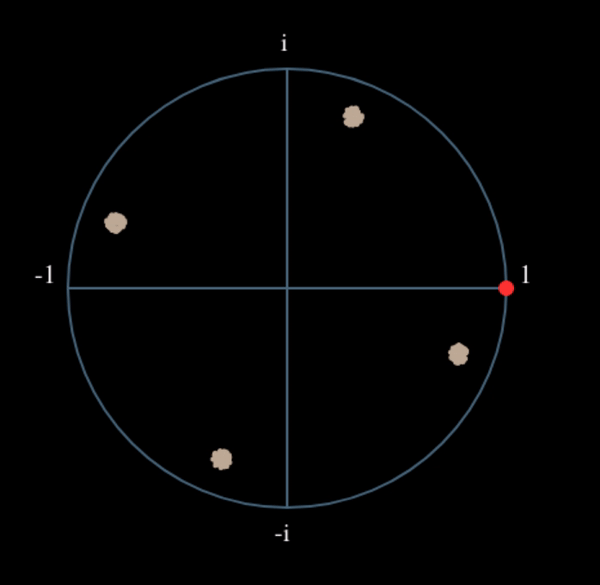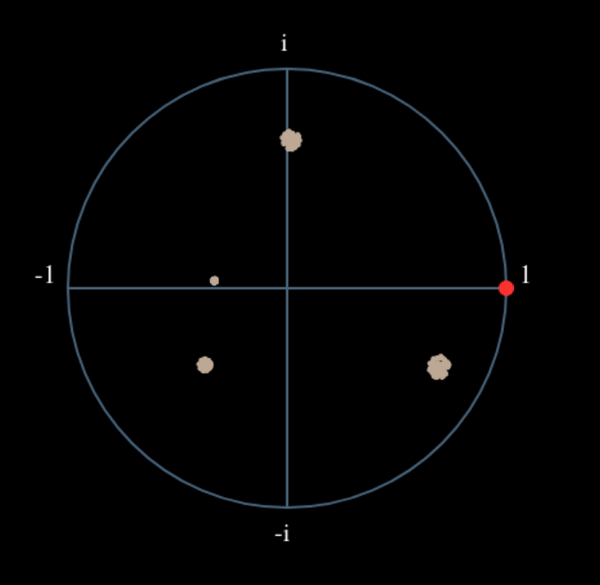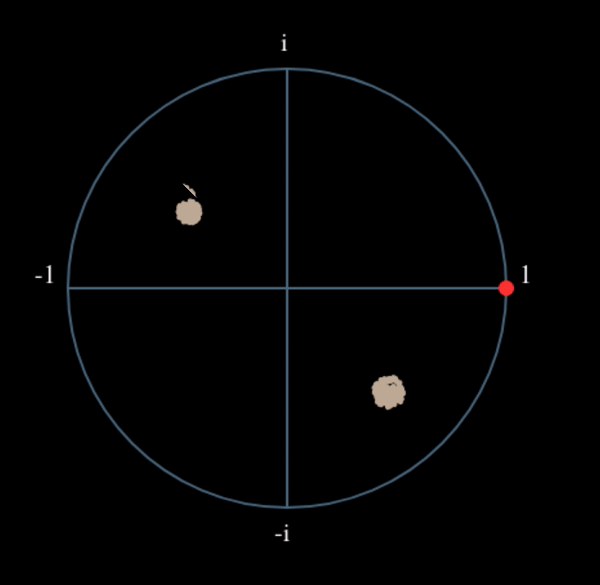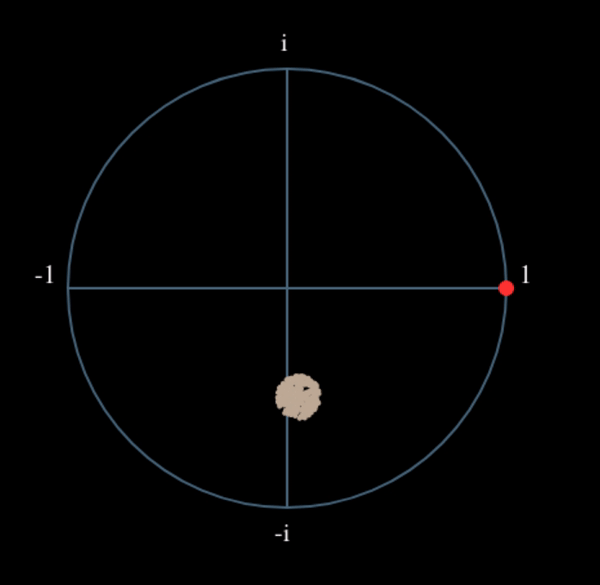
Це все одно стає одним кластером, просто зі зсувом по фазі. Основний висновок полягає в тому, що якщо ви піднесете QPSK до квадрата двічі (а BPSK - один раз), це об’єднає всі чотири кластери точок в один кластер. Чому це корисно? Ну, об’єднуючи кластери, ми по суті видаляємо модуляцію! Якщо всі точки тепер знаходяться в одному кластері, це все одно, що мати купу констант підряд. Це як якщо б модуляції більше не було, і єдине, що залишилося - це синусоїда, викликана зсувом частоти (у нас також є шум, але давайте поки що ігнорувати його). Виходить, що потрібно піднести сигнал до квадрату N разів, де N - це порядок використовуваної схеми модуляції, а це означає, що цей трюк працює лише тоді, коли ви знаєте схему модуляції заздалегідь. Рівняння дійсно має вигляд:

Для нашого випадку BPSK ми маємо схему модуляції 2-го порядку, тому для грубої частотної синхронізації будемо використовувати наступне рівняння:

Ми з’ясували, що відбувається з частиною рівняння , але як щодо синусоїдальної частини (так званої комплексної експоненти)? Як бачимо, до неї додається член , що робить її еквівалентною синусоїді на частоті , а не просто . Простий метод обчислення - це взяти ШПФ сигналу після того, як ми піднесемо його до квадрату N разів і подивимося, де відбувається сплеск. Давайте змоделюємо це на Python. Ми повернемося до генерації нашого BPSK-сигналу, і замість дробової затримки застосуємо до нього частотний зсув, помноживши сигнал на так само, як ми це робили у розділі Фільтри для перетворення фільтра нижніх частот на фільтр верхніх частот.

Використовуючи код з початку цього розділу, додайте до вашого цифрового сигналу частотний зсув +13 кГц. Це може статися безпосередньо перед або відразу після додавання дробової затримки; це не має значення. Незалежно від цього, це повинно відбутися “після” формування імпульсів, але до того, як ми виконаємо будь-які функції на стороні прийому, такі як синхронізація часу.

Тепер, коли у нас є сигнал зі зсувом частоти на 13 кГц, давайте побудуємо графік ШПФ до і після зведення в квадрат, щоб побачити, що відбувається. На цей момент ви вже повинні знати, як робити ШПФ, включаючи операції abs() і fftshift(). Для цієї вправи не має значення, чи берете ви лог, чи ні, чи підносите його до квадрату після застосування функції abs().

Спочатку подивіться на сигнал до піднесення до квадрату (звичайне ШПФ):

psd = np.fft.fftshift(np.abs(np.fft.fft(samples)))
f = np.linspace(-fs/2.0, fs/2.0, len(psd))
plt.plot(f, psd)
plt.show()

Насправді ми не бачимо жодного піку, пов’язаного зі зміщенням несучої. Він перекритий нашим сигналом.

Тепер додамо квадратуру (просто степінь 2, тому що це BPSK):

# Додаємо це перед рядком ШПФ
samples = samples**2

Ми повинні збільшити зображення, щоб побачити, на якій частоті знаходиться пік:

Ви можете спробувати збільшити кількість імітованих символів (наприклад, до 1000 символів), щоб мати достатньо зразків для роботи. Чим більше вибірок буде використано у нашому ШПФ, тим точнішою буде наша оцінка частотного зсуву. Нагадую, що наведений вище код повинен стояти “до” синхронізатора.

Стрибок частоти зсуву з’являється за адресою . Нам потрібно розділити цей бін (26,6 кГц) на 2, щоб отримати остаточну відповідь, яка дуже близька до зсуву частоти на 13 кГц, який ми застосували на початку розділу! Якщо ви погралися з цим числом і воно вже не дорівнює 13 кГц, нічого страшного. Просто переконайтеся, що ви усвідомлюєте, на якому значенні ви його встановили.

Оскільки наша частота дискретизації становить 1 МГц, максимальні частоти, які ми можемо побачити, знаходяться в діапазоні від -500 кГц до 500 кГц. Якщо ми піднесемо наш сигнал до степеня N, це означає, що ми зможемо “побачити” лише частотні зсуви до , або у випадку BPSK +/- 250 кГц. Якби ми приймали сигнал QPSK, то його частота була б лише +/- 125 кГц, а зсув несучої вище або нижче цього значення був би поза межами нашого діапазону за допомогою цього методу. Щоб дати вам уявлення про доплерівський зсув, якби ви передавали в діапазоні 2,4 ГГц, а передавач або приймач рухалися зі швидкістю 60 миль/год (важлива відносна швидкість), це призвело б до зсуву частоти на 214 Гц. Зсув через низьку якість генератора, ймовірно, буде головним винуватцем у цій ситуації.

Насправді виправлення цього зсуву частоти відбувається саме так, як ми імітували зсув спочатку: множенням на комплексну експоненту, тільки з від’ємним знаком, оскільки ми хочемо видалити зсув.

max_freq = f[np.argmax(psd)]
Ts = 1/fs # розраховуємо період дискретизації
t = np.arange(0, Ts*len(samples), Ts) # створюємо вектор часу
samples = samples * np.exp(-1j*2*np.pi*max_freq*t/2.0)

Вам вирішувати, чи хочете ви це виправити або змінити початкове зміщення частоти, яке ми застосували на початку, на менше число (наприклад, 500 Гц), щоб протестувати точну частотну синхронізацію, яку ми зараз навчимося робити.

Точна частотна синхронізація

Далі ми перемкнемо передачу на точну частотну синхронізацію. Попередній трюк більше підходить для грубої синхронізації, і він не є операцією із замкнутим контуром (типу зворотного зв’язку). Але для точної частотної синхронізації нам потрібен контур зворотного зв’язку, через який ми пропускаємо семпли, що знову ж таки буде формою PLL. Наша мета - звести частотний зсув до нуля і утримувати його на цьому рівні, навіть якщо зсув змінюється з часом. Ми повинні постійно відстежувати зміщення. Методи точної частотної синхронізації найкраще працюють з сигналом, який вже було синхронізовано в часі на рівні символів, тому код, який ми обговорюватимемо в цьому розділі, з’явиться після синхронізації в часі.

Ми будемо використовувати техніку, яка називається петлею Костаса. Це форма ШПФ, яка спеціально розроблена для корекції зсуву несучої частоти для цифрових сигналів, таких як BPSK і QPSK. Вона була винайдена Джоном П. Костасом в General Electric в 1950-х роках і мала великий вплив на сучасні цифрові комунікації. Петля Костаса усуває зсув частоти, а також фіксує будь-який зсув фази. Енергія вирівнюється з віссю I. Частота - це лише зміна фази, тому їх можна відстежувати як одне ціле. Петлю Костаса узагальнено за допомогою наступної діаграми (зауважте, що 1/2s не враховано в рівняннях, оскільки вони не мають функціонального значення).

Генератор, керований напругою (VCO) - це просто генератор хвиль sin/cos, який використовує частоту на основі вхідного сигналу. У нашому випадку, оскільки ми моделюємо бездротовий канал, це не напруга, а скоріше рівень, представлений змінною. Він визначає частоту і фазу генерованих синусоїдальних і косинусоїдальних хвиль. Він множить отриманий сигнал на внутрішньо згенеровану синусоїду, намагаючись вирівняти зсув частоти і фази. Ця поведінка схожа на те, як SDR перетворює сигнал вниз і створює гілки I і Q.

Нижче наведено код на Python, який є нашим циклом Костаса:

N = len(samples)
phase = 0
freq = 0
# Наступні два параметри - це те, що потрібно налаштувати, щоб зробити цикл зворотного зв'язку швидшим або повільнішим (що впливає на стабільність)
alpha = 0.132
beta = 0.00932
out = np.zeros(N, dtype=np.complex)
freq_log = []
for i in range(N):
    out[i] = samples[i] * np.exp(-1j*phase) # коригуємо вхідну вибірку на величину, обернену до оціненого фазового зсуву
    error = np.real(out[i]) * np.imag(out[i]) # Це формула похибки для петлі Костаса 2-го порядку (наприклад, для BPSK)

    # Просуваємо цикл (перераховуємо фазу і зсув частоти)
    freq += (beta * error)
    freq_log.append(freq * fs / (2*np.pi)) # перетворення кутової швидкості у Гц для логування
    phase += freq + (alpha * error)

    # Необов'язково: Відрегулюйте фазу так, щоб вона завжди була між 0 і 2pi, пам'ятайте, що фаза обертається навколо кожних 2pi
    while phase >= 2*np.pi:
        phase -= 2*np.pi
    while phase < 0:
        phase += 2*np.pi

# Побудувати графік залежності freq від часу, щоб побачити, скільки часу потрібно для досягнення потрібного зсуву
plt.plot(freq_log,'.-')
plt.show()

Тут багато рядків, тому давайте пройдемося по ним. Деякі рядки прості, а деякі дуже складні. samples - це наші вхідні дані, а out - вихідні. phase і frequency схожі на mu з коду часової синхронізації. Вони містять поточні оцінки зсуву, і на кожній ітерації циклу ми створюємо вихідні відліки шляхом множення вхідних відліків на np.exp(-1j*phase). Змінна error містить метрику “помилки”, і для циклу Костаса 2-го порядку це дуже просте рівняння. Ми множимо дійсну частину відліку (I) на уявну частину (Q), і оскільки Q має дорівнювати нулю для BPSK, функція помилки мінімізується, коли немає фазового або частотного зсуву, який спричиняє зміщення енергії від I до Q. Для петлі Костаса 4-го порядку це все ще відносно просто, але не зовсім в один рядок, оскільки і I, і Q матимуть енергію навіть за відсутності фазового або частотного зсуву, для QPSK. Якщо вам цікаво, як вона виглядає, натисніть нижче, але ми поки що не будемо використовувати її в нашому коді. Причина, чому це працює для QPSK, полягає в тому, що коли ви берете абсолютне значення I і Q, ви отримаєте +1+1j, і якщо немає фазового або частотного зсуву, то різниця між абсолютними значеннями I і Q повинна бути близькою до нуля.

Рівняння похибки петлі Костаса 4-го порядку (для тих, кому цікаво)

# Для QPSK
def phase_detector_4(sample):
    if sample.real > 0:
        a = 1.0
    else
        a = -1.0
    if sample.imag > 0
        b = 1.0
    else
        b = -1.0
    return a * sample.imag - b * sample.real

Змінні alpha і beta визначають швидкість оновлення фази і частоти відповідно. Існує певна теорія, чому я вибрав саме ці два значення, але ми не будемо розглядати її тут. Якщо вам цікаво, ви можете спробувати змінити значення alpha та/або beta і подивитися, що станеться.

Ми записуємо значення freq на кожній ітерації, щоб в кінці побудувати графік і побачити, як петля Костаса сходиться до правильного частотного зсуву. Нам потрібно помножити freq на частоту дискретизації і перевести з кутової частоти в Гц, поділивши на . Зауважте, що якщо ви виконували синхронізацію часу перед циклом Костаса, вам доведеться також поділити на ваше значення sps (наприклад, 8), тому що семпли, які виходять з синхронізації часу, мають частоту, що дорівнює вашій початковій частоті, поділеній на sps.

Нарешті, після перерахунку фази, ми додаємо або забираємо достатню кількість , щоб утримати фазу між 0 і , що обертає фазу навколо.

Наш сигнал до і після петлі Костаса виглядає так:

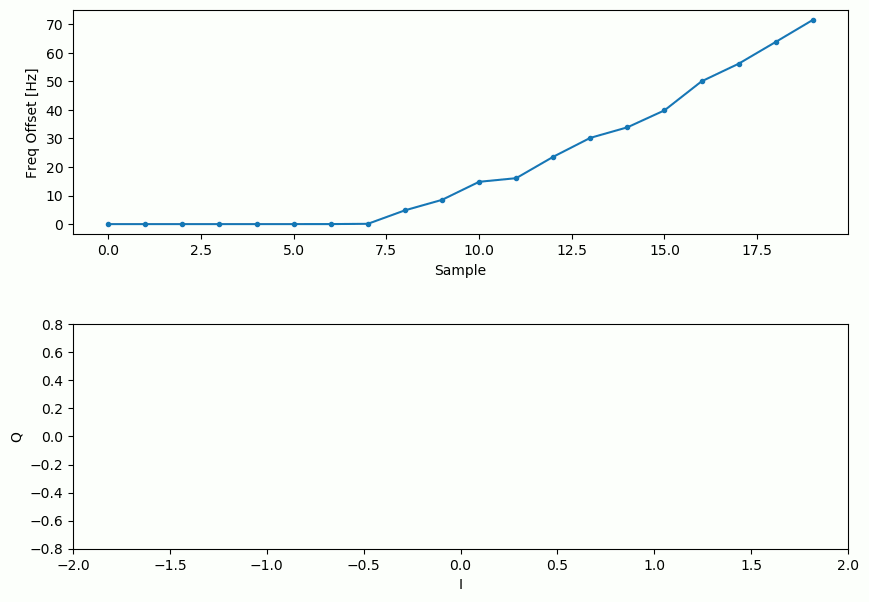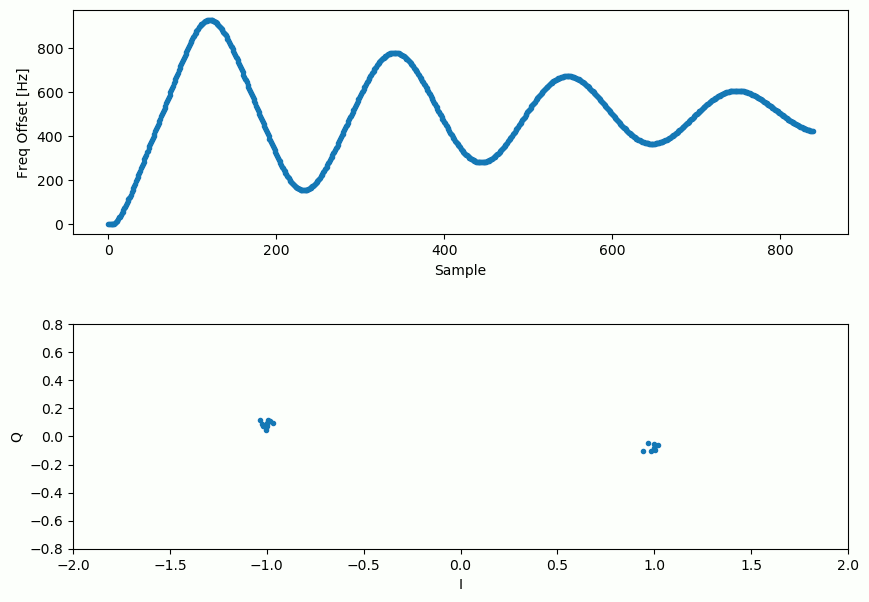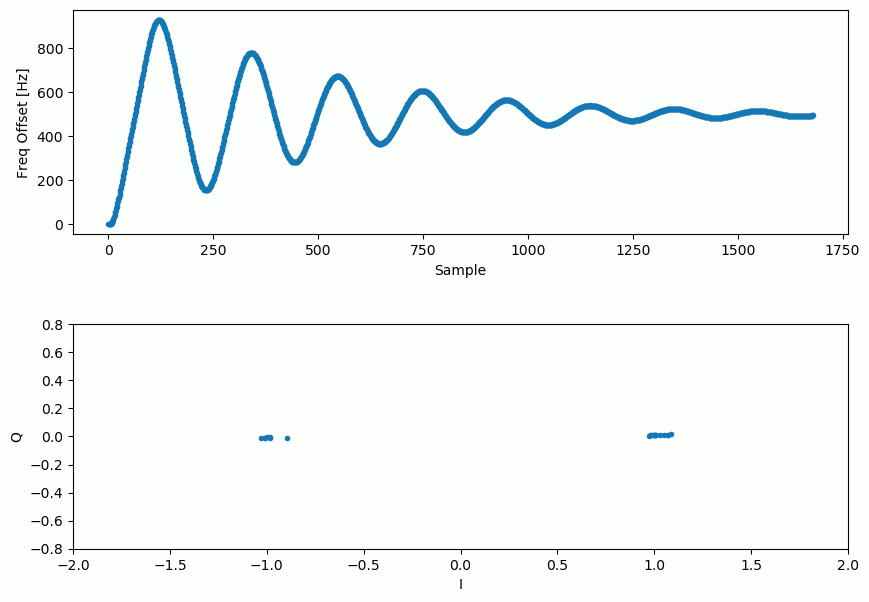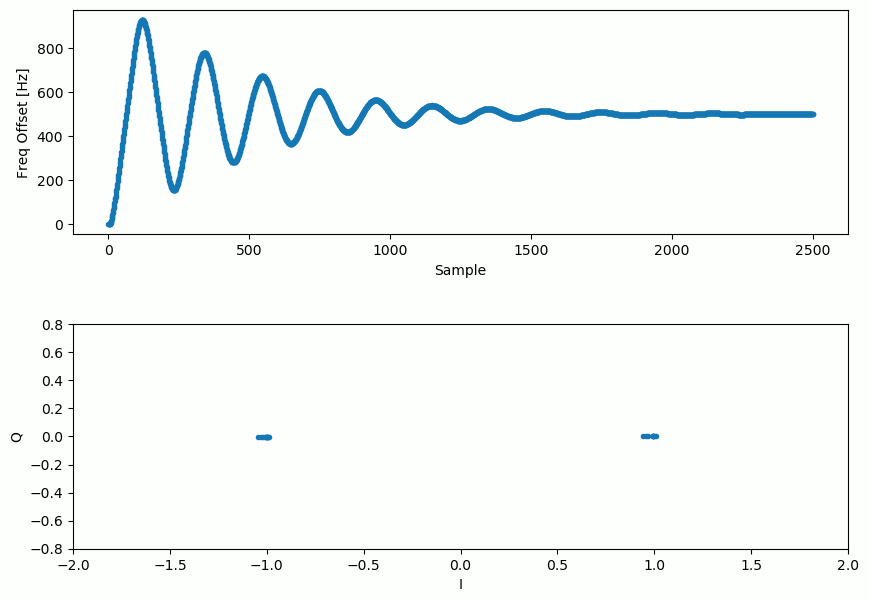
І оцінка зсуву частоти з часом, зупиняючись на правильному зсуві (в цьому прикладі сигналу було використано зсув -300 Гц):

Алгоритму потрібно майже 70 відліків, щоб повністю зафіксуватися на частотному зсуві. Ви можете бачити, що в моєму симульованому прикладі після грубої частотної синхронізації залишилося близько -300 Гц. У вас може бути інакше. Як я вже згадував раніше, ви можете вимкнути грубу частотну синхронізацію і встановити початкове зміщення частоти на будь-яке значення, яке ви хочете, і подивитися, чи зрозуміє це петля Костаса.

Петля Костаса, окрім усунення зсуву частоти, вирівняла наш BPSK-сигнал по I-частині, зробивши добротність знову нульовою. Це зручний побічний ефект петлі Костаса, і він дозволяє петлі Костаса по суті діяти як наш демодулятор. Тепер все, що нам потрібно зробити, це взяти I і подивитися, чи є він більшим або меншим за нуль. Насправді ми не знатимемо, як перетворити від’ємне і додатне значення на 0 і 1, тому що інверсія може бути, а може і не бути; петля Костаса (або наша синхронізація часу) ніяк не може про це дізнатися. Саме тут в гру вступає диференціальне кодування. Воно усуває двозначність, тому що 1 і 0 базуються на тому, чи змінився символ, а не на тому, чи був він +1 чи -1. Якби ми додали диференціальне кодування, ми б все одно використовували BPSK. Ми б додали блок диференціального кодування безпосередньо перед модуляцією на стороні tx і відразу після демодуляції на стороні rx.

Нижче наведено анімацію роботи часової синхронізації плюс частотної синхронізації, часова синхронізація насправді відбувається майже миттєво, але частотна синхронізація займає майже весь час анімації, і це тому, що alpha і beta були встановлені занадто низько, до 0.005 і 0.001 відповідно. Код, використаний для створення цієї анімації, можна знайти тут.

Синхронізація кадрів

Ми обговорили, як виправити будь-які часові, частотні та фазові зсуви в отриманому сигналі. Але більшість сучасних протоколів зв’язку не є просто потоковою передачею бітів зі 100% робочим циклом. Замість цього вони використовують пакети/кадри. На приймачі нам потрібно мати можливість визначити, коли починається новий кадр. Зазвичай заголовок кадру (на рівні MAC) містить інформацію про кількість байт у кадрі. Ми можемо використовувати цю інформацію, щоб дізнатися довжину кадру, наприклад, в одиницях виміру або символах. Тим не менш, визначення початку кадру є окремим завданням. Нижче показано приклад структури кадру WiFi. Зверніть увагу, що найпершим передається заголовок фізичного рівня, а перша половина цього заголовка є “преамбулою”. Ця преамбула містить послідовність синхронізації, яку приймач використовує для виявлення початку кадрів, і ця послідовність відома приймачу заздалегідь.

Поширеним і простим методом виявлення цих послідовностей на приймачі є перехресна кореляція отриманих зразків з відомою послідовністю. Коли послідовність зустрічається, ця крос-кореляція нагадує автокореляцію (з додаванням шуму). Зазвичай послідовності, вибрані для преамбул, мають гарні автокореляційні властивості, наприклад, автокореляція послідовності створює єдиний сильний пік в точці 0 і не має інших піків. Одним з прикладів є коди Баркера, у 802.11/WiFi послідовність Баркера довжиною 11 використовується для швидкостей 1 і 2 Мбіт/с:

+1 +1 +1 -1 -1 -1 +1 -1 -1 +1 -1

Ви можете думати про це як про 11 символів BPSK. Ми можемо дуже легко подивитися на автокореляцію цієї послідовності в Python:

import numpy as np
import matplotlib.pyplot as plt
x = [1,1,1,-1,-1,-1,1,-1,-1,1,-1]
plt.plot(np.correlate(x,x,'same'),'.-')
plt.grid()
plt.show()

Ви бачите, що по центру стоїть 11 (довжина послідовності), а для всіх інших затримок - -1 або 0. Це добре працює для пошуку початку кадру, тому що по суті інтегрує енергію 11 символів, намагаючись створити 1 бітовий сплеск на виході крос-кореляції. Насправді, найскладніша частина виявлення початку кадру - це визначення правильного порогу. Ви не хочете, щоб кадри, які насправді не є частиною вашого протоколу, викликали його спрацьовування. Це означає, що на додаток до перехресної кореляції вам також потрібно виконати певну нормалізацію потужності, яку ми тут не розглядатимемо. Вибираючи поріг, ви повинні знайти компроміс між ймовірністю виявлення та ймовірністю хибних тривог. Пам’ятайте, що заголовок кадру містить інформацію, тому деякі хибні тривоги є нормальними; ви швидко виявите, що це насправді не кадр, коли спробуєте декодувати заголовок, і CRC неминуче зазнає невдачі (тому що це насправді не кадр). Проте, хоча деякі хибні спрацьовування є нормальними, відсутність виявлення кадру взагалі є поганим явищем.

Ще одна послідовність з чудовими автокореляційними властивостями - це послідовності Задоффа-Чу, які використовуються в LTE. Їх перевага полягає в тому, що вони є наборами; ви можете мати кілька різних послідовностей, які мають хороші автокореляційні властивості, але вони не спрацьовуватимуть одна з одною (тобто також мають хороші властивості перехресної кореляції, коли ви перехресно корелюєте різні послідовності в наборі). Завдяки цій властивості різним вежам мобільного зв’язку будуть присвоєні різні послідовності, щоб телефон міг не тільки знайти початок кадру, але й знати, з якої вежі він отримує сигнал.