4. Цифрова модуляція

У цьому розділі ми обговоримо фактичну передачу даних за допомогою цифрової модуляції та бездротових символів! Ми розробимо сигнали, які передають “інформацію”, наприклад, одиниці та нулі, використовуючи схеми модуляції, такі як ASK, PSK, QAM та FSK. Ми також обговоримо IQ-графіки та сузір’я, а наприкінці глави наведемо кілька прикладів на Python.

Основне завдання модуляції - втиснути якомога більше даних у якомога меншу частку спектра. З точки зори техніки, це значить, що ми хочемо максимізувати “спектральну ефективність” в одиницях вимірювання біт/сек/Гц. Передача одиниць і нулів з більшою швидкістю, збільшує і смугу пропускання що потрібна для нашого сигналу (згадайте тему про властивості перетворення Фур’є), а це означає, що буде використано більше смуга з спектру. Окрім прискорення швидкості передачі, ми також розглянемо інші методи. При виборі способу модуляції є багато компромісів, але також є і простір для творчості.

Символи

Увага, новий термін! Наш сигнал передачі буде складатися з “символів”. Кожен символ буде нести певну кількість бітів інформації, і ми будемо передавати символи один за одним, тисячі або навіть мільйони разів поспіль.

Як спрощений приклад, уявімо, що у нас є дріт і ми передаємо одиниці та нулі, використовуючи високі та низькі рівні напруги. Символ - це одне з двох цих значень (одиниці або нуля):

У наведеному вище прикладі кожен символ представляє один біт. Як можна передати більше одного біта одним символом? Розглянемо сигнали, які передаються по кабелю Ethernet, що визначений в стандарті IEEE під назвою IEEE 802.3 1000BASE-T. При звичайному режимі роботи Ethernet використовує 4-рівневу амплітудну модуляцію (2 біти на символ) з тривалістю символів 8 нс.

Спробуйте відповісти на ці питання:

1. Скільки біт в секунду передається в наведеному вище прикладі?

2. Скільки пар цих дротів потрібно для передачі даних зі швидкістю 1 гігабіт/с?

3. Якщо схема модуляції має 16 різних рівнів, скільки біт припадає на один символ?

4. Якщо схема модуляції має 16 різних рівнів і тривалість символу 8 нс, то розрахуйте швидкість передачі даних в біт на секунду?

Відповіді

1. 250 Мбіт/с - (1/8e-9)*2

2. Чотири (саме стільки мають ethernet-кабелі)

3. 4 біти на символ - log_2(16)

4. 0.5 Гбіт/с - (1/8e-9)*4

Бездротові символи

Питання: Чому ми не можемо безпосередньо передавати сигнал ethernet, преведені на рисунку вище? Існує багато причин, дві з яких є основними:

1. Низькі частоти вимагають величезних антен, а вищенаведений сигнал містить частоти аж до постійного струму (0 Гц). Передавати постійний струм ми не можемо.

2. Прямокутні хвилі займають надмірну кількість спектру для певної швидкості в бітах на секунду - згадайте розділ Частотний домен де було показано, що різкі зміни у часовій області призводять до розширення смуги пропускання/спектру сигналу:

Що ми робимо для бездротових сигналів, так це починаємо з несучої, яка є просто синусоїдою. Наприклад, FM-радіо використовує несучу частоту 101,1 МГц або 100,3 МГц. Ми модулюємо цю несучу певним чином (є багато способів). Для FM-радіо це аналогова модуляція, а не цифрова, але це те саме поняття, що й цифрова модуляція.

Яким чином ми можемо модулювати несучу? Інший спосіб поставити те саме питання: які різні властивості синусоїди?

1. Амплітуда

2. Фаза

3. Частота

Ми можемо модулювати наші дані на носій, змінюючи один (або більше) з цих трьох параметрів.

Амплітудна маніпуляція (ASK)

Амплітудна маніпуляція (ASK) - це перша схема цифрової модуляції, яку ми обговоримо, оскільки амплітудна модуляція є найпростішою для візуалізації з трьох властивостей синусоїди. Ми буквально модулюємо амплітуду несучої. Ось приклад дворівневої АСК, яка називається 2-ASK:

Зверніть увагу, що середнє значення дорівнює нулю; ми завжди надаємо перевагу цьому, коли це можливо.

Ми можемо використовувати більше двох рівнів, що дозволяє отримати більше бітів на символ. Нижче наведено приклад 4-ASK. У цьому випадку кожен символ містить 2 біти інформації.

Питання: Скільки символів показано у фрагменті сигналу вище? Скільки бітів представлено загалом?

Відповіді

20 символів, тобто 40 біт інформації

Як ми можемо створити цей сигнал в цифровому вигляді, за допомогою коду? Все, що нам потрібно зробити, це створити вектор з N відліків на символ, а потім помножити цей вектор на синусоїду. Це модулює сигнал на несучу (синусоїда виступає в якості такої несучої). У прикладі нижче показано 2-ASK з 10 відліками на символ.

Верхній графік показує дискретні відліки, представлені червоними крапками, тобто наш цифровий сигнал. Нижній графік показує, як виглядає результуючий модульований сигнал, який можна було б передавати в ефір. У реальних системах частота несучої зазвичай набагато вища за швидкість зміни символів. У цьому прикладі в кожному символі лише три цикли синусоїди, але на практиці їх можуть бути тисячі, залежно від того, наскільки високо в спектрі передається сигнал.

Фазова маніпуляція (PSK)

Тепер давайте розглянемо модуляцію фази так само, як ми це робили з амплітудою. Найпростішою формою є двійкова PSK, також відома як BPSK, де є два рівні фази:

1. Без зміни фази

2. Зміна фази на 180 градусів

Приклад BPSK (зверніть увагу на зміну фази):

Дивитися на такі графіки не дуже цікаво:

Замість цього ми зазвичай представляємо фазу на комплексній площині.

IQ-графіки/сузір’я

Ви вже бачили IQ-графіки раніше в підрозділі комплексних чисел розділу Вибірка IQ, але зараз ми використаємо їх у новий і цікавий спосіб. Для заданого символу ми можемо показати амплітуду і фазу на IQ-діаграмі. Для прикладу BPSK ми сказали, що маємо фази 0 і 180 градусів. Нанесімо ці дві точки на IQ-діаграму. Ми візьмемо значення 1. На практиці не має значення, яке значення ви використовуєте; більше значення означає більшу потужність сигналу, але ви також можете просто збільшити коефіцієнт підсилення підсилювача.

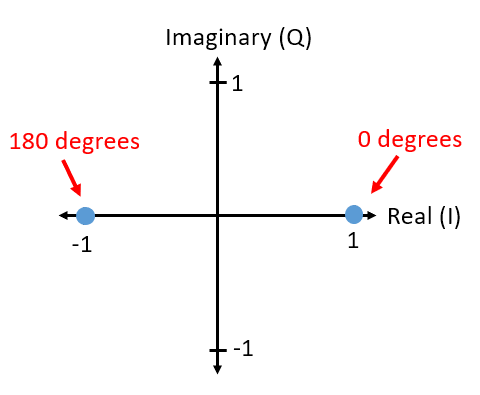
Наведена вище IQ-діаграма показує, що ми будемо передавати, а точніше набір символів, з яких ми будемо передавати. Вона не показує несучу, тому ви можете думати про неї, як про представлення символів у базовій смузі. Коли ми показуємо набір можливих символів для даної схеми модуляції, ми називаємо його “сузір’ям”. Багато схем модуляції можна визначити за допомогою сузір’я.

Для прийому і декодування BPSK ми можемо використовувати дискретизацію IQ, про яку ми дізналися в минулому розділі, і дослідити, куди потрапляють точки на графіку IQ. Однак, через бездротовий канал буде випадковий поворот фази, оскільки сигнал буде мати випадкову затримку, коли він проходить через повітря між антенами. Випадковий поворот фази можна виправити різними методами, про які ми дізнаємося пізніше. Ось приклад кількох різних способів, якими BPSK-сигнал може з’явитися на приймачі (це без урахування шуму):

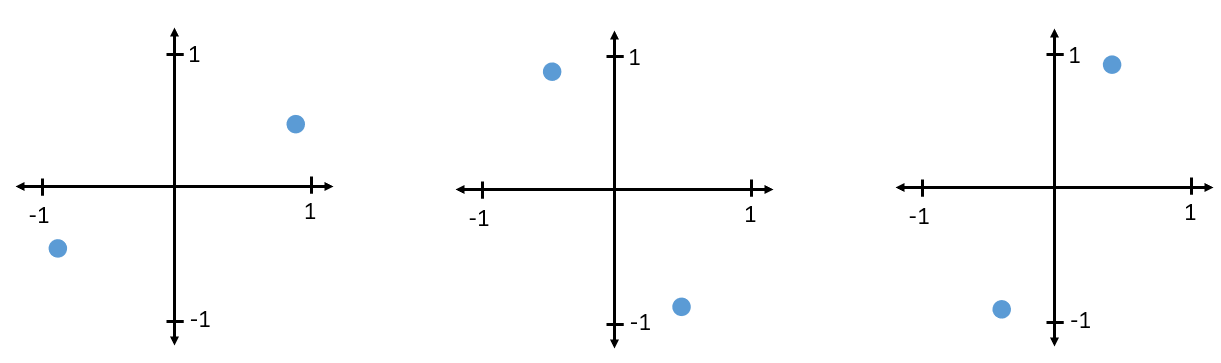
Повернемося до PSK. Що, якщо ми хочемо отримати чотири різних рівні фази? Тобто 0, 90, 180 і 270 градусів. У цьому випадку на IQ-діаграмі це буде виглядати так, як на діаграмі, і утворює схему модуляції, яку ми називаємо квадратурною фазовою маніпуляцією (QPSK):

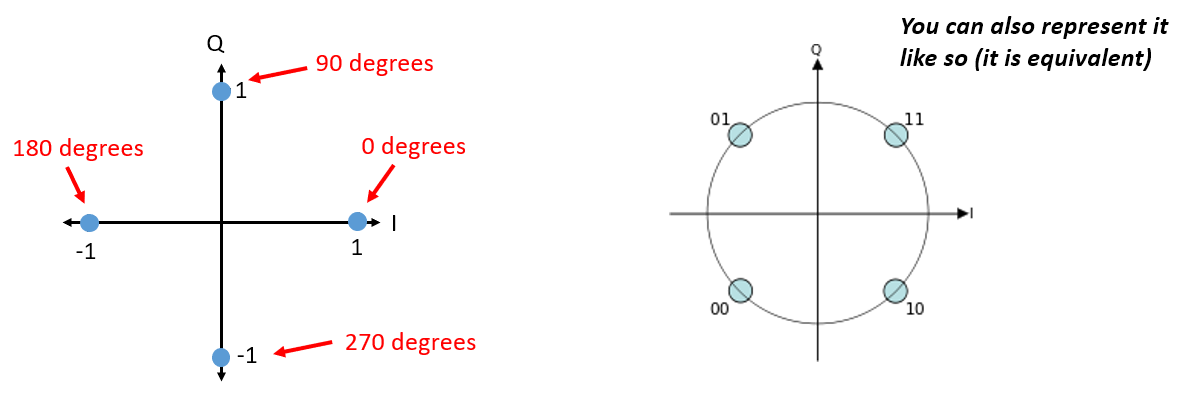
Для PSK ми завжди маємо N різних фаз, рівномірно розподілених навколо 360 градусів для досягнення найкращих результатів. Ми часто показуємо одиничне коло, щоб підкреслити, що всі точки мають однакову величину:

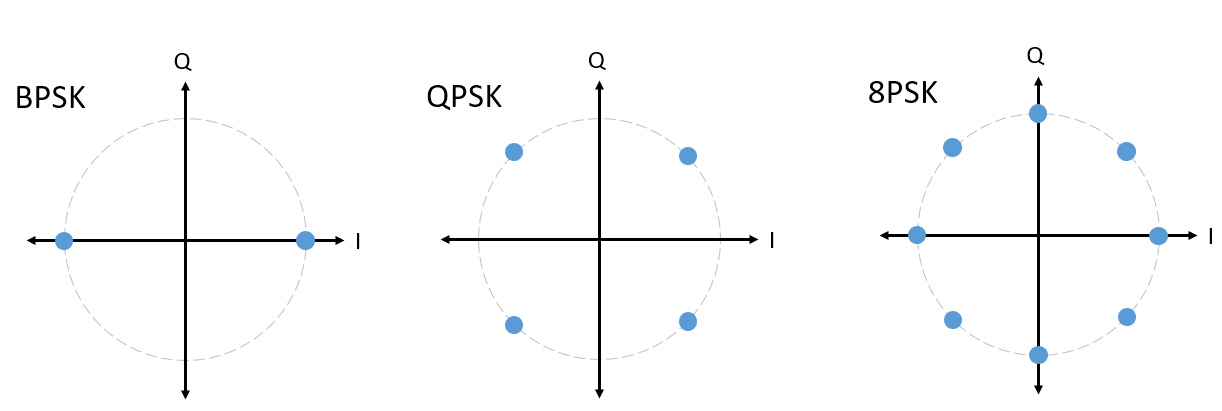
Питання: Що поганого у використанні схеми PSK, як на наведеному нижче зображенні? Чи є це дійсною схемою модуляції PSK?

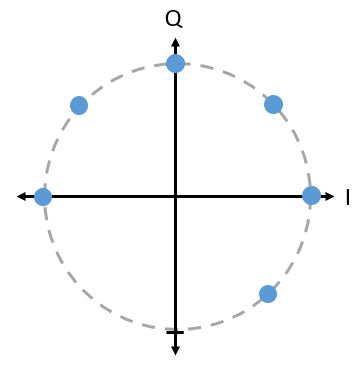
Відповідь

У цій схемі PSK немає нічого неправильного. Ви, звичайно, можете використовувати її, але, оскільки символи розташовані нерівномірно, ця схема не настільки ефективна, як могла б бути. Ефективність схеми стане зрозумілою, коли ми обговоримо, як шум впливає на наші символи. Коротка відповідь полягає в тому, що ми хочемо залишити якомога більше місця між символами, якщо є шум, щоб символ не був інтерпретований приймачем як один з інших (неправильних) символів. Ми не хочемо, щоб 0 був прийнятий як 1.

Давайте на мить повернемося до ASK. Зауважте, що ми можемо показати ASK на графіку IQ так само, як і PSK. Ось графік IQ для 2-ASK, 4-ASK і 8-ASK у біполярній конфігурації, а також 2-ASK і 4-ASK в уніполярній конфігурації.

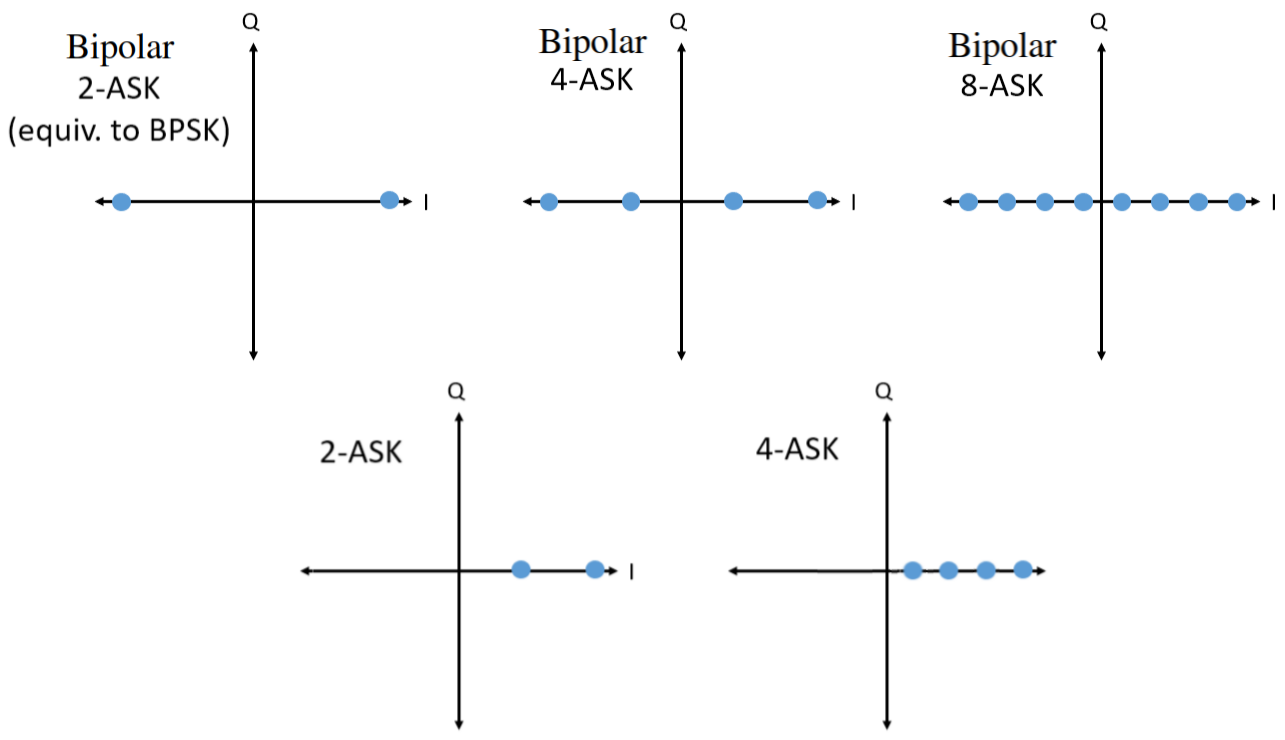
Як ви могли помітити, біполярна 2-ASK і BPSK однакові. Зсув фази на 180 градусів - це те саме, що помножити синусоїду на -1. Ми називаємо його BPSK, ймовірно, тому, що PSK використовується набагато частіше, ніж ASK.

Квадратурна амплітудна модуляція (QAM)

Що, якщо ми об’єднаємо ASK і PSK? Ми називаємо таку схему модуляції квадратурною амплітудною модуляцією (QAM). Зазвичай QAM виглядає приблизно так:

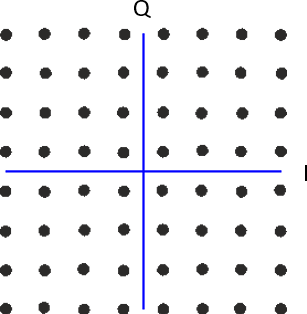
Ось деякі інші приклади QAM:

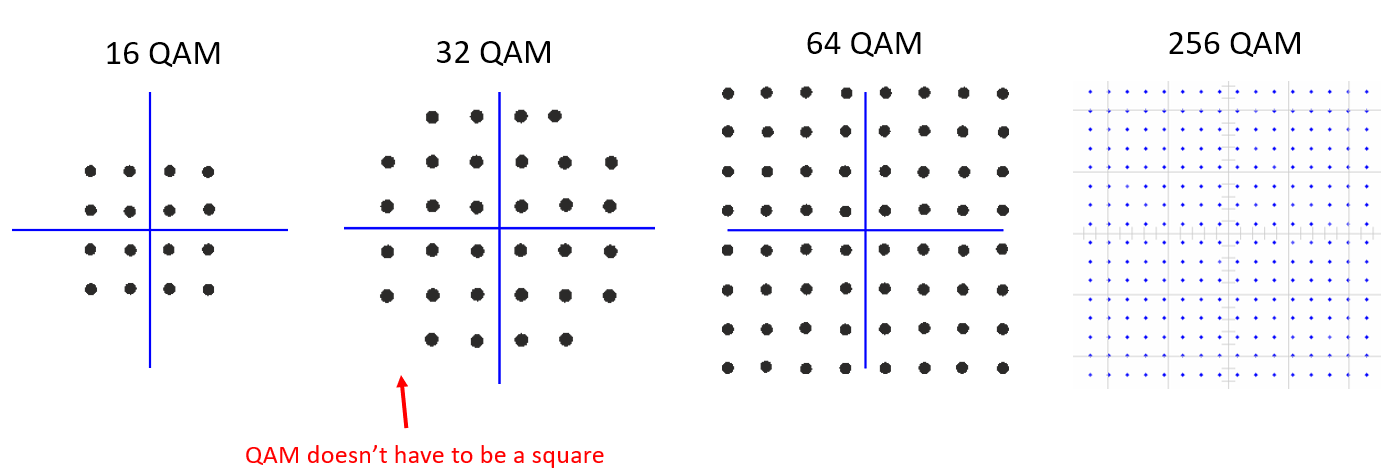
Для схеми модуляції QAM ми можемо технічно поставити точки де завгодно на діаграмі IQ, оскільки фаза і амплітуда модулюються. “Параметри” даної схеми QAM найкраще визначити, показавши сузір’я QAM. Крім того, ви можете перерахувати значення I і Q для кожної точки, як показано нижче для QPSK:

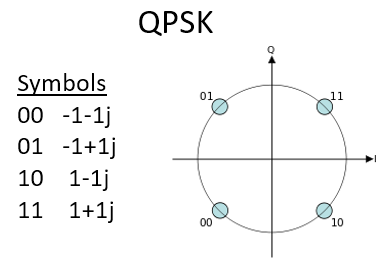
Зауважте, що більшість схем модуляції, за винятком різних ASK і BPSK, досить важко “побачити” в часовій області. Щоб довести мою думку, наведемо приклад QAM у часовій області. Чи можете ви розрізнити фазу кожного символу на зображенні нижче? Це важко.

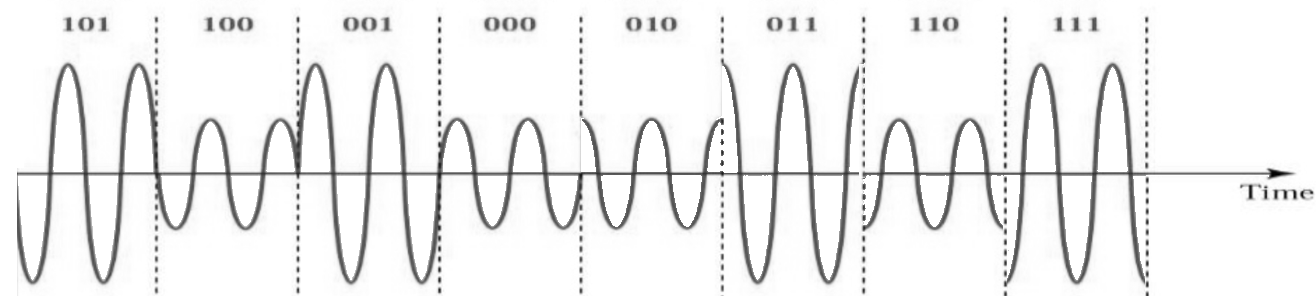
Враховуючи складність розрізнення схем модуляції в часовій області, ми надаємо перевагу використанню IQ-діаграм замість відображення сигналу в часовій області. Тим не менш, ми можемо показати сигнал у часовій області, якщо є певна структура пакетів або послідовність символів має значення.

Частотна маніпуляція (FSK)

Останньою у списку є частотна маніпуляція (Frequency Shift Keying, FSK). FSK досить простий для розуміння - ми просто перемикаємося між N частотами, де кожна частота - це один можливий символ. Однак, оскільки ми модулюємо несучу, це насправді наша несуча частота +/- ці N частот. Наприклад, ми можемо перебувати на несучій частоті 1,2 ГГц і зміщуватися між цими чотирма частотами:

1. 1.2005 ГГц

2. 1.2010 ГГц

3. 1.1995 ГГц

4. 1.1990 ГГц

У наведеному вище прикладі буде 4-FSK, і на кожен символ припадатиме по два біти. Сигнал 4-FSK у частотній області може виглядати приблизно так:

Якщо ви використовуєте FSK, ви повинні поставити важливе питання: Якою має бути відстань між частотами? Ми часто позначаємо цю відстань як у Гц. Ми хочемо уникнути перекриття в частотній області, щоб приймач знав, на якій частоті використовується даний символ, тому має бути достатньо великою. Ширина кожної несучої у частотній області є функцією нашої швидкості передачі символів. Чим більше символів на секунду, тим коротші символи, а отже, ширша смуга пропускання (згадайте обернену залежність між масштабуванням часу і частоти). Чим швидше ми передаємо символи, тим ширшою буде кожна несуча, і, відповідно, тим більшим буде , щоб уникнути перекриття несучих. У цьому підручнику ми не будемо вдаватися у подробиці побудови FSK.

IQ-діаграми не можна використовувати для відображення різних частот. Вони показують амплітуду і фазу. Хоча можна показати FSK в часовій області, але більше ніж 2 частоти ускладнюють розрізнення символів:

Зверніть увагу, що FM-радіо використовує частотну модуляцію (FM), яка є аналоговою версією FSK. Замість дискретних частот, між якими ми перестрибуємо, FM-радіо використовує безперервний аудіосигнал для модуляції частоти несучої. Нижче наведено приклад FM і AM модуляції, де “сигнал” вгорі - це аудіосигнал, який модулюється на несучу частоту.

У цьому підручнику ми розглядаємо переважно цифрові форми модуляції.

Диференціальне кодування

У багатьох протоколах бездротового (і дротового) зв’язку ви, швидше за все, зіткнетеся з так званим диференціальним кодуванням. Щоб продемонструвати його корисність, розглянемо прийом сигналу BPSK. Коли сигнал пролітає повітрям, він зазнає випадкової затримки між передавачем і приймачем, що спричиняє випадкове обертання сузір’я, як ми вже згадували раніше. Коли приймач синхронізується з ним і вирівнює BPSK по осі “I”, він не має можливості дізнатися, чи є зсув у фазі на 180 градусів чи ні, оскільки сузір’я симетричне. Одним з варіантів є передача символів, значення яких одержувач знає заздалегідь, змішаних з інформацією, відомих як пілотні символи. Одержувач може використовувати ці відомі символи, щоб визначити, який кластер є 1 або 0, у випадку BPSK. Пілотні символи повинні надсилатися через певний проміжок часу, пов’язаний з тим, наскільки швидко змінюється бездротовий канал, що в кінцевому підсумку зменшує швидкість передачі даних.

Замість того, щоб підмішувати пілотні символи до форми сигналу, що передається, ми можемо використовувати диференціальне кодування. У своїй найпростішій формі, яка використовується для BPSK, диференціальне кодування передбачає передачу 0, коли вхідний біт збігається з попереднім вихідним бітом, і передачу 1, коли вони відрізняються. Таким чином, ми все ще передаємо ту саму кількість бітів (за винятком одного додаткового біта, необхідного на початку для початку вихідної послідовності), але тепер нам не потрібно турбуватися про 180-градусну неоднозначність фази. Щоб продемонструвати, як це працює, розглянемо передачу послідовності бітів [1, 1, 0, 0, 0, 0, 1, 0] з використанням BPSK. Припустимо, що ми почнемо вихідну послідовність з 1; насправді не має значення, чи ви використовуєте 1 або 0. Після застосування диференціального кодування ми в кінцевому підсумку передамо [1, 0, 1, 1, 1, 1, 0, 0]. Одиниці та нулі все ще зіставляються з позитивними та негативними символами, про які ми говорили раніше. Можливо, буде простіше візуалізувати вхідні та вихідні послідовності, складені у стек таким чином:

Великим недоліком використання диференціального кодування є те, що якщо у вас є бітова помилка, це призведе до двох бітових помилок. Альтернативою використанню диференціального кодування для BPSK є періодичне додавання пілотних символів, які є символами, вже відомими приймачу, і він може використовувати відомі значення, щоб не тільки визначити, який кластер є 1, а який 0, але й обернути багатопроменевість, спричинену каналом. Одна з проблем з пілот-символами полягає в тому, що бездротовий канал може змінюватися дуже швидко, порядку десятків або сотень символів, якщо це рухомий приймач і/або передавач, тому вам знадобляться пілотні символи досить часто, щоб відображати зміну каналу. Отже, якщо бездротовий протокол приділяє велику увагу зменшенню складності приймача, як, наприклад, RDS, який ми розглядаємо у розділі Наскрізний приклад, він може використовувати диференційне кодування.

Приклад на Python

Як короткий приклад на Python, давайте згенеруємо QPSK на базовій смузі і побудуємо графік сузір’я.

Хоча ми могли б згенерувати складні символи безпосередньо, почнемо з того, що QPSK має чотири символи з інтервалом 90 градусів навколо одиничного кола. Ми будемо використовувати 45, 135, 225 і 315 градусів для наших точок. Спочатку ми згенеруємо випадкові числа від 0 до 3 і виконаємо математичні дії, щоб отримати потрібні нам градуси, а потім перетворимо їх у радіани.

import numpy as np
import matplotlib.pyplot as plt

num_symbols = 1000

x_int = np.random.randint(0, 4, num_symbols) # від 0 до 3
x_degrees = x_int*360/4.0 + 45 # 45, 135, 225, 315 градусів
x_radians = x_degrees*np.pi/180.0 # sin() і cos() беруть в радіанах
x_symbols = np.cos(x_radians) + 1j*np.sin(x_radians) # отримуємо наші комплексні символи QPSK
plt.plot(np.real(x_symbols), np.imag(x_symbols), '.')
plt.grid(True)
plt.show()

Подивіться, як всі символи, які ми згенерували, перекриваються. Шум відсутній, тому всі символи мають однакове значення. Давайте додамо трохи шуму:

phase_noise = np.random.randn(len(x_symbols)) * 0.1 # adjust multiplier for "strength" of phase noise
r = x_symbols * np.exp(1j*phase_noise)

Розглянемо, як адитивний білий гаусівський шум (AWGN) створює рівномірний розподіл навколо кожної точки сузір’я. Якщо шуму занадто багато, то символи починають перетинати межу (чотири квадранти) і будуть інтерпретуватися приймачем як неправильний символ. Спробуйте збільшити noise_power, поки цього не станеться.

Для тих, хто зацікавлений в імітації фазового шуму, який може виникнути внаслідок фазового джиттера у локальному генераторі (LO), замініть r на:

phase_noise = np.random.randn(len(x_symbols)) * 0.1 # підлаштовуємо множник під "силу" фазового шуму
r = x_symbols * np.exp(1j*phase_noise)

Ви навіть можете комбінувати фазовий шум з AWGN, щоб отримати повний ефект:

На цьому ми зупинимося. Якби ми хотіли побачити, як виглядає QPSK-сигнал у часовій області, нам потрібно було б згенерувати кілька відліків на символ (у цій вправі ми зробили лише 1 відлік на символ). Ви дізнаєтеся, чому потрібно генерувати кілька відліків на символ, коли ми обговоримо формування імпульсів. Вправа з Python у розділі Pulse Shaping буде продовжена з того місця, на якому ми зупинилися.

Додаткова інформація

1. https://en.wikipedia.org/wiki/Differential_coding