22. Практична робота з Phaser¶

У цій главі ми використовуємо Analog Devices Phaser, (також відомий як CN0566 або ADALM-PHASER), який є 8-канальною недорогою фазованою решіткою SDR, що поєднує в собі PlutoSDR, Raspberry Pi і формувач променя ADAR1000, призначений для роботи на частоті близько 10,25 ГГц. Ми розглянемо етапи налаштування та калібрування, а потім розглянемо кілька прикладів формування променя на Python. Для тих, хто не має фазообертача, ми додали скріншоти та анімації того, що побачить користувач.

Огляд апаратного забезпечення¶

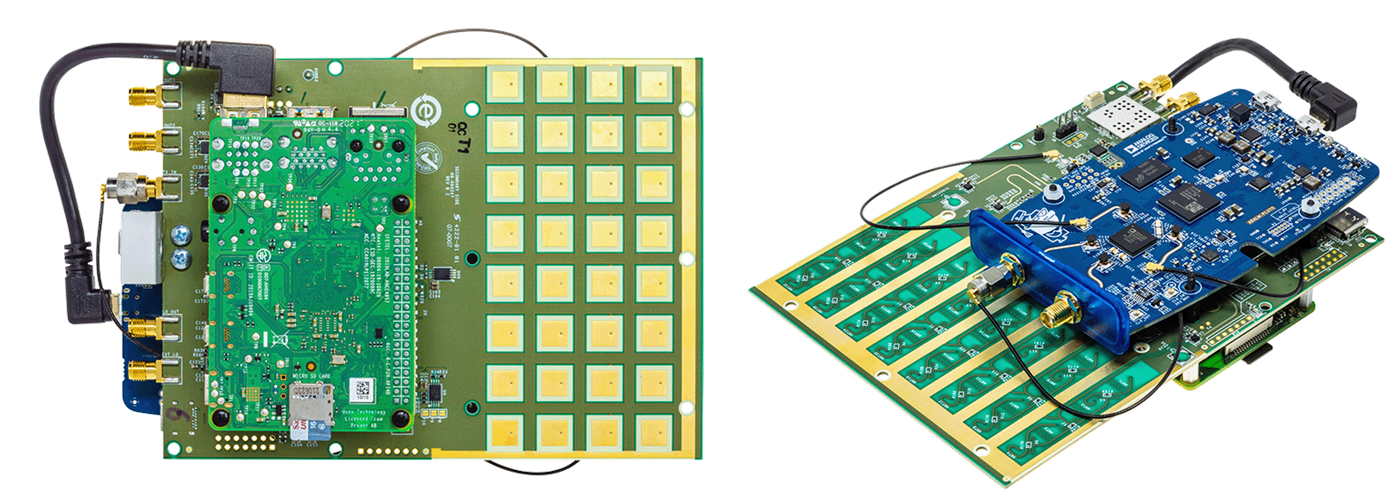
Phaser - це одна плата, що містить фазовану антенну решітку та низку інших компонентів, до якої з одного боку підключено Raspberry Pi, а з іншого боку - Pluto. Високорівнева блок-схема показана нижче. Деякі моменти, на які слід звернути увагу:

Хоча це виглядає як 32-елементний двовимірний масив, насправді це 8-елементний одновимірний масив
Використовуються обидва канали прийому на Плутоні (другий канал використовує роз’єм u.FL)
LO на борту використовується для перетворення прийнятого сигналу з частоти близько 10,25 ГГц до частоти близько 2 ГГц, щоб Плутон міг його прийняти
Кожен ADAR1000 має чотири фазообертачі з регульованим коефіцієнтом підсилення, і всі чотири канали підсумовуються перед відправкою на Плутон
Фазообертач по суті містить два “підмасиви”, кожен з яких містить чотири канали
Нижче не показані GPIO і послідовні сигнали від Raspberry Pi, які використовуються для керування різними компонентами фазообертача

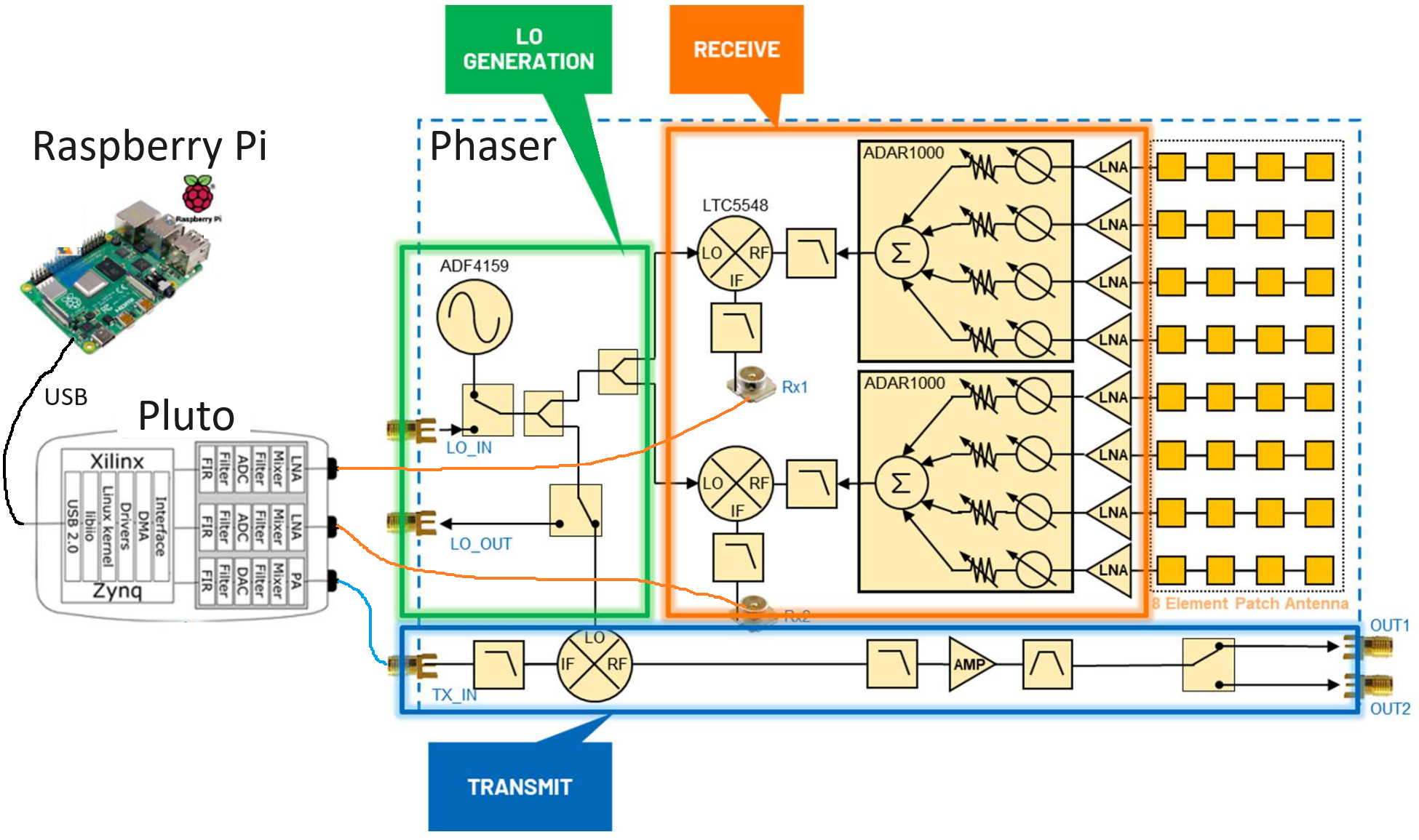
Компоненти фазера (CN0566), включаючи ADF4159, LTC5548, ADAR1000

Наразі проігноруємо передавальну частину фазоінвертора, оскільки в цій главі ми використовуватимемо пристрій HB100 лише як тестовий передавач. ADF4159 - це синтезатор частоти, який виробляє тон з частотою до 13 ГГц, який ми називаємо локальним генератором або LO. Цей ЛО подається на мікшер LTC5548, який може здійснювати як висхідне, так і низхідне перетворення, хоча ми використовуватимемо його для низхідного перетворення. Для низхідного перетворення він приймає сигнал LO, а також сигнал в діапазоні від 2 до 14 ГГц, і перемножує їх разом, що призводить до зсуву частоти. Результуючий сигнал може бути в діапазоні від постійного струму до 6 ГГц, хоча ми націлені на частоту близько 2 ГГц. ADAR1000 - це 4-канальний аналоговий формувач променя, тому Фазер використовує два з них. Аналоговий формувач променя має незалежно регульовані фазові перемикачі і коефіцієнт підсилення для кожного каналу, що дозволяє затримувати в часі і послаблювати кожен канал перед підсумовуванням в аналоговому діапазоні (в результаті чого виходить один канал). На фазообертачі кожен ADAR1000 виводить сигнал, який перетворюється вниз, а потім приймається Плутоном. Використовуючи Raspberry Pi, ми можемо контролювати фазу і посилення всіх восьми каналів в реальному часі, щоб виконувати формування променя. У нас також є можливість виконувати двоканальне цифрове формування променя/обробку масивів, що обговорюється в наступному розділі.

Для тих, хто цікавиться, нижче наведено дещо детальнішу блок-схему.

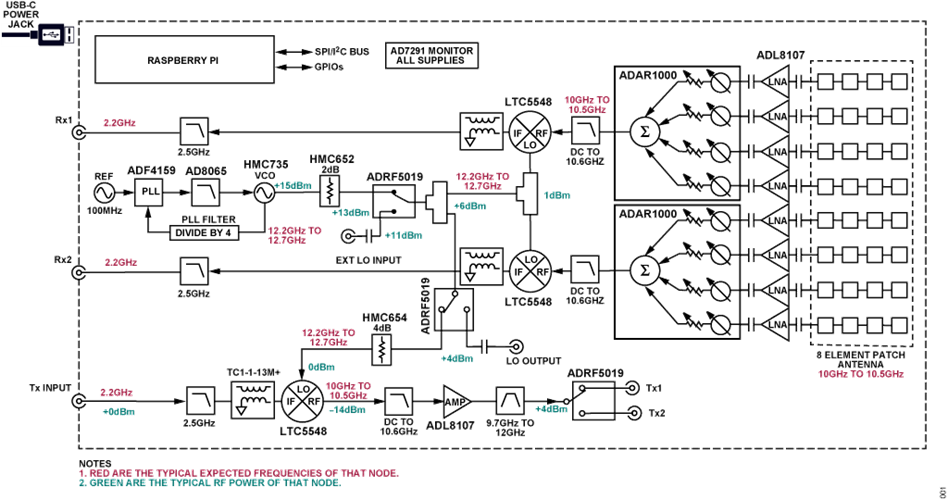
Підготовка SD-карти¶

Будемо вважати, що ви використовуєте Raspberry Pi на борту Phaser (безпосередньо, з монітором/клавіатурою/мишею). Це спрощує налаштування, оскільки Analog Devices публікує готовий образ SD-карти з усіма необхідними драйверами та програмним забезпеченням. Ви можете завантажити образ SD-карти і знайти інструкції по створенню образу SD-карти тут. Образ базується на Raspberry Pi OS і включає все необхідне програмне забезпечення, яке вам знадобиться, вже встановлене.

Підготовка обладнання¶

Підключіть CENTER порт micro-USB Pluto до Raspberry Pi
За бажанням, акуратно вкрутіть штатив у кріплення для штатива
Ми припускаємо, що ви використовуєте HDMI-дисплей, USB-клавіатуру і USB-мишу, підключені до Raspberry Pi
Підключіть живлення до Pi і плати Phaser через порт Type-C Phaser (CN0566), тобто НЕ підключайте блок живлення до USB C Raspberry Pi.

Встановлення програмного забезпечення¶

Після завантаження в Raspberry Pi за допомогою образу попередньої збірки, використовуючи стандартний користувач/пароль аналог/аналог, рекомендується виконати наступні кроки:

wget https://github.com/mthoren-adi/rpi_setup_stuff/raw/main/phaser/phaser_sdcard_setup.sh
sudo chmod +x phaser_sdcard_setup.sh
./phaser_sdcard_setup.sh
sudo reboot

sudo raspi-config

Для отримання додаткової допомоги у налаштуванні Phaser зверніться до Phaser wiki quickstart page.

Налаштування HB100¶

HB100, що постачається з Phaser, - це недорогий доплерівський радарний модуль, який ми будемо використовувати як тестовий передавач, оскільки він передає безперервний тон на частоті близько 10 ГГц. Він працює від 2 батарейок типу АА або від настільного джерела живлення 3 В, і коли він увімкнений, на ньому світиться яскравий червоний світлодіод.

Оскільки HB100 є недорогим і використовує дешеві радіочастотні компоненти, його частота передачі варіюється від одиниці до одиниці, понад сотні МГц, що є діапазоном, який перевищує найвищу пропускну здатність, яку ми можемо отримати, використовуючи Плутон (56 МГц). Тому, щоб переконатися, що ми налаштували наш Pluto і понижуючий перетворювач таким чином, щоб завжди отримувати сигнал HB100, ми повинні визначити частоту передачі HB100. Це робиться за допомогою прикладної програми від Analog Devices, яка виконує розгортку частоти і обчислює ШПФ, шукаючи пік. Переконайтеся, що ваш HB100 увімкнений і знаходиться в безпосередній близькості від Phaser, а потім запустіть утиліту з..:

cd ~/pyadi-iio/examples/phaser
python phaser_find_hb100.py

Він повинен створити файл з назвою hb100_freq_val.pkl у тій самій директорії. Цей файл містить частоту передачі HB100 в Гц (мариновану, тому її не можна переглянути у відкритому вигляді), яку ми будемо використовувати на наступному кроці.

Калібрування¶

Нарешті, нам потрібно відкалібрувати фазовану решітку. Для цього потрібно утримувати HB100 на мушці решітки (0 градусів). Сторона HB100 зі штрих-кодом є стороною, яка передає сигнал, тому її слід тримати на відстані кількох футів від фазообертача, прямо перед ним і по центру, а потім спрямувати прямо на фазообертач. На наступному кроці ви можете поекспериментувати з різними кутами та орієнтаціями, а поки що давайте запустимо утиліту калібрування:

python phaser_examples.py cal

Це створить ще два пікл-файли: phase_cal_val.pkl і gain_cal_val.pkl, в тому ж каталозі. Кожен з них містить масив з 8 чисел, що відповідають значенням фази і підсилення, необхідним для калібрування кожного каналу. Ці значення є унікальними для кожного фазообертача, оскільки вони можуть змінюватися під час виробництва. Наступні запуски цієї утиліти призведуть до дещо інших значень, що є нормальним явищем.

Попередньо зібраний приклад програми¶

Тепер, коли ми відкалібрували наш лазер і знайшли частоту HB100, ми можемо запустити приклад програми від Analog Devices.

python phaser_gui.py

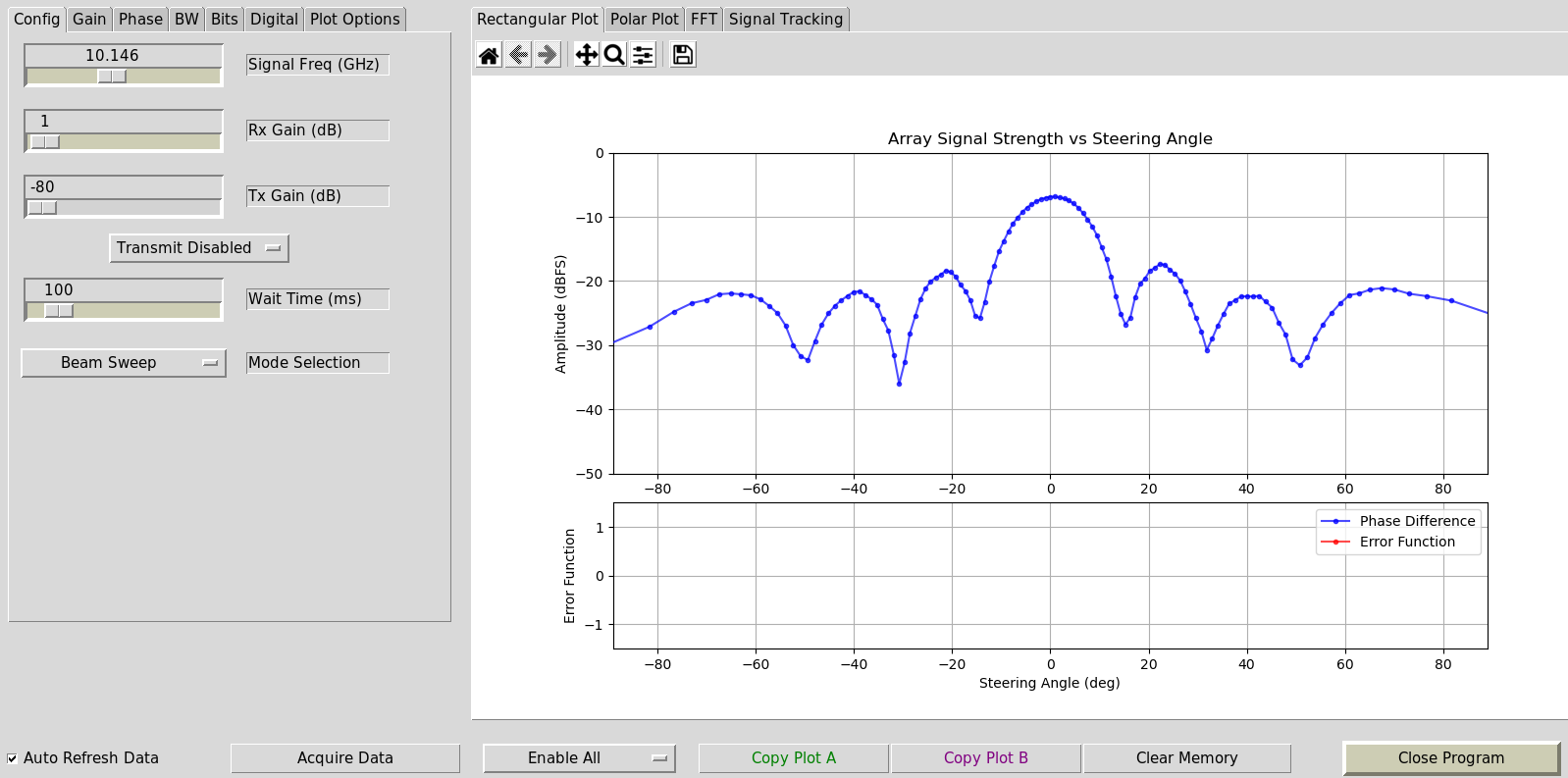
Якщо ви встановите прапорець “Автоматичне оновлення даних” в нижньому лівому кутку, програма почне працювати. Коли ви тримаєте HB100 у мушці фазера, ви побачите щось подібне до наведеного нижче.

Приклад графічного інтерфейсу фазера від Analog Devices

Phaser на Python¶

Тепер ми зануримося в практичну частину на Python. Для тих, хто не має Phaser, надаються скріншоти та анімації.

Ініціалізація Phaser і Pluto¶

Наступний код на Python налаштовує наш Phaser і Pluto. До цього моменту ви вже повинні були виконати кроки калібрування, які створюють три файли pickle. Переконайтеся, що ви виконуєте скрипт Python, наведений нижче, у тому самому каталозі, де знаходяться ці файли.

Тут є багато налаштувань, тому нічого страшного, якщо ви не прочитаєте весь фрагмент коду нижче, просто зауважте, що ми використовуємо частоту дискретизації 30 МГц, ручне посилення, яке ми встановили дуже низьким, ми встановили однакове значення посилення для всіх елементів і спрямували масив у бік бурової лінії (0 градусів).

import time
import sys
import matplotlib.pyplot as plt
import numpy as np
import pickle
from adi import ad9361
from adi.cn0566 import CN0566

phase_cal = pickle.load(open("phase_cal_val.pkl", "rb"))
gain_cal = pickle.load(open("gain_cal_val.pkl", "rb"))
signal_freq = pickle.load(open("hb100_freq_val.pkl", "rb"))
d = 0.014 # міжелементна відстань антени

phaser = CN0566(uri="ip:localhost")
sdr = ad9361(uri="ip:192.168.2.1")
phaser.sdr = sdr
print("PlutoSDR та CN0566 підключено!")

time.sleep(0.5) # рекомендовано Analog Devices

phaser.configure(device_mode="rx")

# Встановіть всі елементи антени на половину шкали - типовий HB100 матиме достатньо потужності сигналу.
gain = 64 # 64 - це приблизно половина шкали
for i in range(8):
    phaser.set_chan_gain(i, gain, apply_cal=False)

# Наводимо промінь на мушку (нуль градусів)
phaser.set_beam_phase_diff(0.0)

# Інші налаштування SDR, не надто важливі для розуміння
sdr._ctrl.debug_attrs["adi,frequency-division-duplex-mode-enable"].value = "1"
sdr._ctrl.debug_attrs["adi,ensm-enable-txnrx-control-enable"].value = "0" # Вимкнути керування виводами, щоб spi міг змінювати стани
sdr._ctrl.debug_attrs["initialize"].value = "1"
sdr.rx_enabled_channels = [0, 1] # увімкнути Rx1 та Rx2
sdr._rxadc.set_kernel_buffers_count(1) # Не очищати застарілі буфери
sdr.tx_hardwaregain_chan0 = int(-80) # Переконайтеся, що канали Tx ослаблені (або вимкнені)
sdr.tx_hardwaregain_chan1 = int(-80)

# Ці налаштування є базовими налаштуваннями PlutoSDR, які ми бачили раніше
sample_rate = 30e6
sdr.sample_rate = int(sample_rate)
sdr.rx_buffer_size = int(1024) # кількість відліків у буфері
sdr.rx_rf_bandwidth = int(10e6) # смуга пропускання аналогового фільтра

 # Ручне регулювання підсилення (без автоматичного регулювання), щоб ми могли розгорнути кут і побачити піки/нулі
sdr.gain_control_mode_chan0 = "manual"
sdr.gain_control_mode_chan1 = "manual"
sdr.rx_hardwaregain_chan0 = 10 # дБ, 0 - найнижчий коефіцієнт підсилення. HB100 досить гучний
sdr.rx_hardwaregain_chan1 = 10 # dB

sdr.rx_lo = int(2.2e9) # Плутон налаштується на цю частоту

# Налаштуйте PLL фазоінвертора (ADF4159 на борту) на пониження частоти HB100 до 2.2 ГГц плюс невеликий зсув
offset = 1000000 # додаємо невелике довільне зміщення, щоб ми не були прямо на 0 Гц, де є стрибок постійного струму
phaser.lo = int(signal_freq + sdr.rx_lo - offset)

Отримання семплів з Плутона¶

На цьому етапі фазер і Плутон налаштовані і готові до роботи. Тепер ми можемо почати отримувати дані з Плутона. Давайте візьмемо один пакет з 1024 відліків, а потім зробимо ШПФ кожного з двох каналів.

# Беремо кілька відліків (скільки б ми не встановили rx_buffer_size), пам'ятаємо, що ми приймаємо по 2 каналах одночасно
data = sdr.rx()

# Робимо ШПФ
PSD0 = 10*np.log10(np.abs(np.fft.fftshift(np.fft.fft(data[0])))**2)
PSD1 = 10*np.log10(np.abs(np.fft.fftshift(np.fft.fft(data[1])))**2)
f = np.linspace(-sample_rate/2, sample_rate/2, len(data[0]))

# Часовий графік допомагає нам перевірити, що ми бачимо HB100 і що ми не перенасичені (тобто коефіцієнт підсилення не є занадто високим)
plt.subplot(2, 1, 1)
plt.plot(data[0].real) # Побудувати лише дійсну частину графіка
plt.plot(data[1].real)
plt.xlabel("Точка даних")
plt.ylabel("Вихід АЦП")

# PSD показують, де знаходиться HB100 і перевіряють, що обидва канали працюють
plt.subplot(2, 1, 2)
plt.plot(f/1e6, PSD0)
plt.plot(f/1e6, PSD1)
plt.xlabel("Частота [МГц]")
plt.ylabel("Рівень сигналу [дБ]")
plt.tight_layout()
plt.show()

Те, що ви побачите на цьому етапі, залежатиме від того, чи увімкнений ваш HB100 і куди він спрямований. Якщо ви тримаєте його на відстані кількох футів від фазера і спрямовуєте до центру, ви побачите щось на зразок цього:

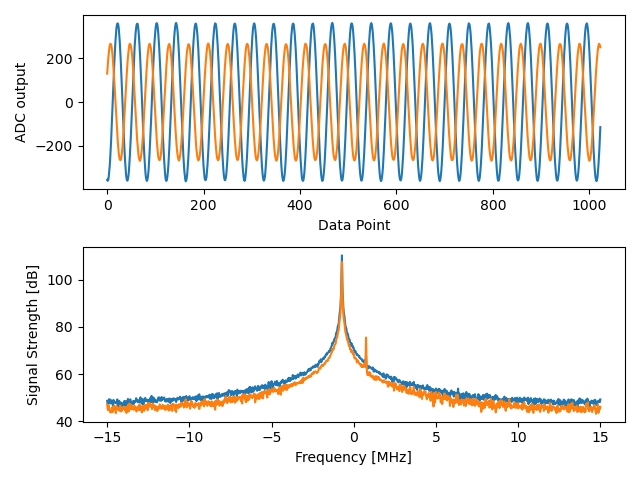
Зверніть увагу на сильний сплеск біля 0 Гц, 2-й коротший сплеск - це просто артефакт, який можна ігнорувати, оскільки він знаходиться приблизно на 40 дБ нижче. Верхній графік, що показує часову область, відображає реальну частину двох каналів, тому відносна амплітуда між ними буде дещо відрізнятися залежно від того, де ви тримаєте HB100.

Виконання формування променя¶

Далі, давайте, власне, розгорнемо фазу! У наступному коді ми змінюємо фазу від від’ємних 180 до додатних 180 градусів з кроком у 2 градуси. Зверніть увагу, що це не кут, на який вказує формувач променя; це різниця фаз між сусідніми каналами. Ми повинні обчислити кут приходу, що відповідає кожному кроку фази, використовуючи знання швидкості світла, радіочастоти прийнятого сигналу і відстані між елементами фазообертача. Різниця фаз між сусідніми елементами задається формулою:

\[\phi = \frac{2 \pi d}{\lambda} \sin(\theta_{AOA})\]

де \(\theta_{AOA}\) - кут приходу сигналу відносно антени, \(d\) - відстань між антенами в метрах, а \(\lambda\) - довжина хвилі сигналу. Використовуючи формулу для довжини хвилі і розв’язуючи для \(\theta_{AOA}\), отримаємо:

\[\theta_{AOA} = \sin^{-1}\left(\frac{c \phi}{2 \pi f d}\right)\]

Ви побачите це, коли ми обчислимо steer_angle нижче:

powers = [] # основний результат DOA
angle_of_arrivals = []
for phase in np.arange(-180, 180, 2): # розгортка на кут
    print(phase)
    # встановити різницю фаз між сусідніми каналами пристроїв
    for i in range(8):
        channel_phase = (phase * i + phase_cal[i]) % 360.0 # У Analog Devices це значення було кратне phase_step_size (2.8125 або 360/2**6bits), але це не здається необхідним
        phaser.elements.get(i + 1).rx_phase = channel_phase
    phaser.latch_rx_settings() # застосовуємо налаштування

    steer_angle = np.degrees(np.arcsin(max(min(1, (3e8 * np.radians(phase)) / (2 * np.pi * signal_freq * phaser.element_spacing)), -1))) # Аргумент arcsin має бути в межах від 1 до -1, інакше numpy видасть попередження
    # Якщо ви дивитеся на сторону масиву Phaser (32 квадрати), то додайте *-1 до steer_angle
    angle_of_arrivals.append(steer_angle)
    data = phaser.sdr.rx() # отримуємо пакет відліків
    data_sum = data[0] + data[1] # підсумовуємо два підмасиви (у кожному підмасиві 4 канали вже підсумовано)
    power_dB = 10*np.log10(np.sum(np.abs(data_sum)**2))
    powers.append(power_dB)
    # на додаток до того, щоб просто взяти потужність сигналу, ми також можемо зробити ШПФ, а потім взяти значення максимального біну, ефективно відфільтрувавши шум, результати вийшли майже однаковими в моїх тестах
    #PSD = 10*np.log10(np.abs(np.fft.fft(data_sum * np.blackman(len(data_sum))))**2) # у дБ

powers -= np.max(powers) # нормалізуємо, щоб max було на рівні 0 дБ

plt.plot(angle_of_arrivals, powers, '.-')
plt.xlabel("Кут приходу")
plt.ylabel("Величина [дБ]")
plt.show()

Для кожного значення phase (пам’ятайте, що це фаза між сусідніми елементами) ми встановлюємо фазові зсуви, попередньо додавши значення калібрування фази і примусивши градуси бути між 0 і 360. Потім ми беремо одну партію відліків за допомогою rx(), підсумовуємо два канали і обчислюємо потужність сигналу. Потім будуємо графік залежності потужності від кута падіння. Результат має виглядати приблизно так:

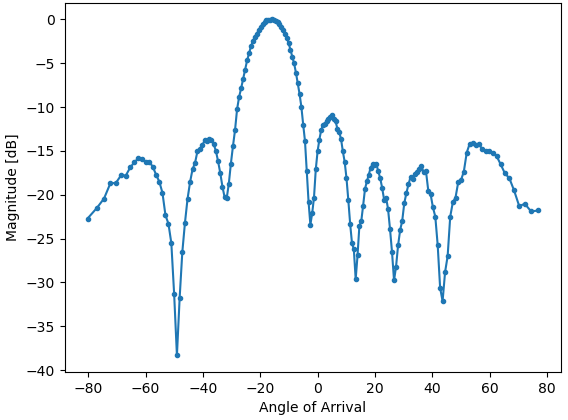
У цьому прикладі HB100 тримався трохи збоку від мушки.

Якщо ви хочете отримати полярну діаграму спрямованості, ви можете використати наступне:

# Полярний графік
fig, ax = plt.subplots(subplot_kw={'projection': 'polar'})
ax.plot(np.deg2rad(angle_of_arrivals), powers) # вісь x у радіанах
ax.set_rticks([-40, -30, -20, -10, 0]) # Менше радіальних тиків
ax.set_thetamin(np.min(angle_of_arrivals)) # у градусах
ax.set_thetamax(np.max(angle_of_arrivals))
ax.set_theta_direction(-1) # збільшити за годинниковою стрілкою
ax.set_theta_zero_location('N') # зробити 0 градусів точкою вгору
ax.grid(True)
plt.show()

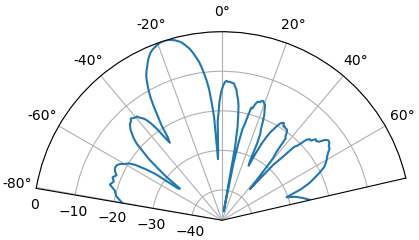
Одиночна розгортка фазера за допомогою полярного графіка

Взявши максимум, ми можемо оцінити напрямок приходу сигналу!

У реальному часі та з просторовим звуженням¶

Тепер давайте поговоримо про просторове звуження. Поки що ми залишили регулювання підсилення кожного каналу на однакових значеннях, так що всі вісім каналів підсумовуються однаково. Подібно до того, як ми застосовували вікно перед ШПФ, ми можемо застосувати вікно в просторовій області, застосувавши ваги до цих восьми каналів. Ми використаємо ті самі віконні функції, такі як Ганнінга, Хеммінга тощо. Давайте також налаштуємо код для роботи в реальному часі, щоб зробити його трохи цікавішим:

plt.ion() # потрібна для перегляду в реальному часі
print("Запуск, для зупинки використовуйте control-c")
try:
    while True:
        powers = [] # основний результат DOA
        angle_of_arrivals = []
        for phase in np.arange(-180, 180, 6): # розгортка на кут
            # встановлюємо різницю фаз між сусідніми каналами пристроїв
            for i in range(8):
                channel_phase = (phase * i + phase_cal[i]) % 360.0 # У Analog Devices це значення було кратне phase_step_size (2.8125 або 360/2**6bits), але це не здається необхідним
                phaser.elements.get(i + 1).rx_phase = channel_phase

            # встановлюємо коефіцієнти підсилення, включаючи gain_cal, за допомогою яких можна застосувати конусність. спробуйте кожен з них!
            gain_list = [127] * 8 # прямокутне вікно          [127, 127, 127, 127, 127, 127, 127, 127]
            #gain_list = np.rint(np.hamming(8) * 127)         # [ 10, 32, 82, 121, 121, 82, 32, 10]
            #gain_list = np.rint(np.hanning(10)[1:-1] * 127)  # [ 15, 52, 95, 123, 123, 95, 52, 15]
            #gain_list = np.rint(np.blackman(10)[1:-1] * 127) # [ 6, 33, 80, 121, 121, 80, 33, 6]
            #gain_list = np.rint(np.bartlett(10)[1:-1] * 127) # [ 28, 56, 85, 113, 113, 85, 56, 28]
            for i in range(8):
                channel_gain = int(gain_list[i] * gain_cal[i])
                phaser.elements.get(i + 1).rx_gain = channel_gain

            phaser.latch_rx_settings() # застосувати налаштування

            steer_angle = np.degrees(np.arcsin(max(min(1, (3e8 * np.radians(phase)) / (2 * np.pi * signal_freq * phaser.element_spacing)), -1))) # аргумент arcsin має бути між 1 та -1, інакше numpy видасть попередження
            angle_of_arrivals.append(steer_angle)
            data = phaser.sdr.rx() # отримуємо пакет відліків
            data_sum = data[0] + data[1] # підсумовуємо два підмасиви (у кожному підмасиві 4 канали вже підсумовано)
            power_dB = 10*np.log10(np.sum(np.abs(data_sum)**2))
            powers.append(power_dB)

        powers -= np.max(powers) # нормалізуємо так, щоб max було на рівні 0 дБ

        # Перегляд у реальному часі
        plt.plot(angle_of_arrivals, powers, '.-')
        plt.xlabel("Кут приходу")
        plt.ylabel("Величина [дБ]")
        plt.draw()
        plt.pause(0.001)
        plt.clf()
except KeyboardInterrupt:
    sys.exit() # вийти з python

Ви повинні побачити версію попередньої вправи у реальному часі. Спробуйте перемикати gain_list, щоб погратися з різними вікнами. Ось приклад прямокутного вікна (тобто без функції розгортання вікна):

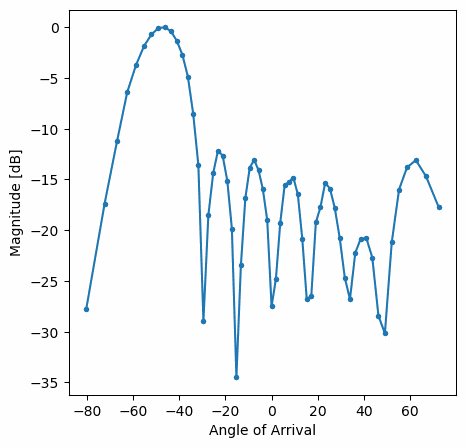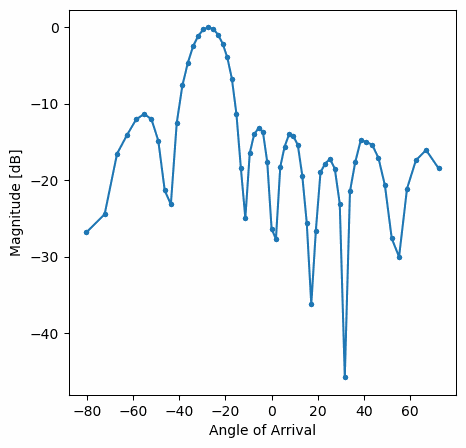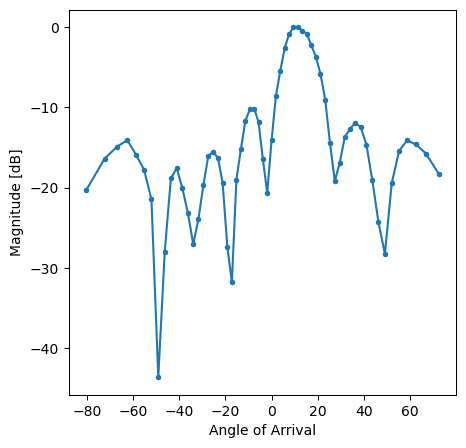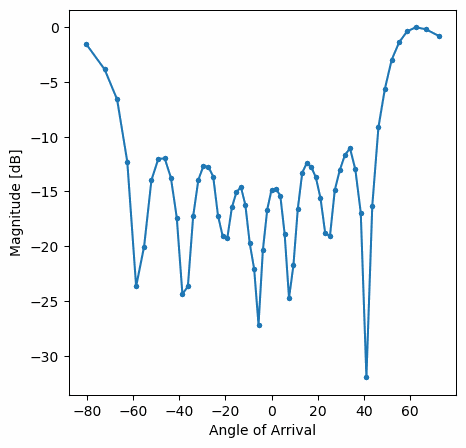
Анімація формування променя за допомогою фазера і прямокутного вікна

а ось приклад вікна Hamming:

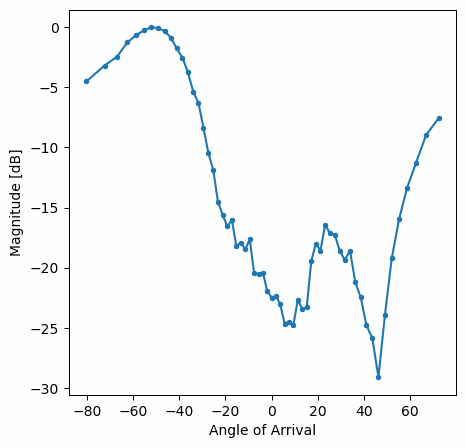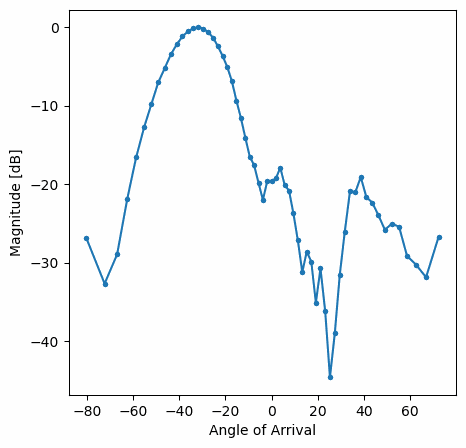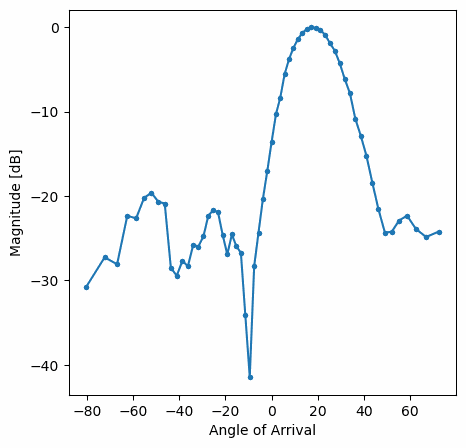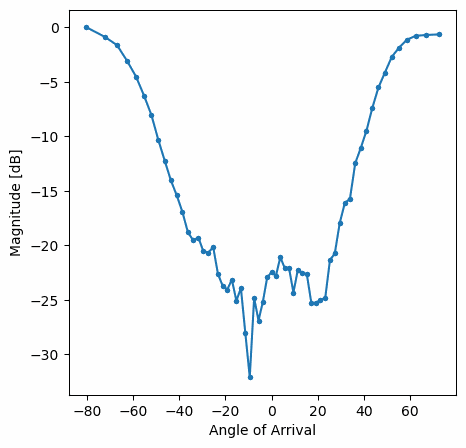
Анімація формування променя за допомогою фазера і вікна Hamming

Зверніть увагу на відсутність бічних граней для вікна Hamming. Насправді, кожне вікно, крім Прямокутного, значно зменшить бічні пелюстки, але натомість головна пелюстка стане трохи ширшою.

Монопульсове відстеження¶

До цього моменту ми виконували окремі розгортки, щоб знайти кут приходу тестового передавача (HB100). Але припустімо, що ми хочемо безперервно приймати сигнал зв’язку чи радара, який може рухатися й змінювати кут приходу з часом. Цей процес називається відстеженням і передбачає, що у нас вже є приблизна оцінка кута приходу (тобто початкова розгортка виявила потрібний сигнал). Ми використаємо монопульсове відстеження для адаптивного оновлення ваг, щоб головна пелюстка з часом залишалася спрямованою на сигнал, хоча варто зазначити, що існують й інші методи відстеження, окрім монопульсу.

Запатентована у 1943 році Робертом Пейджем з Naval Research Laboratory (NRL), базова ідея монопульсового відстеження полягає у використанні двох променів, обидва дещо зміщені від поточного кута приходу (або принаймні нашої оцінки), але розташовані по різні боки, як показано на діаграмі нижче.

Діаграма монопульсового променя, що показує два промені та сумарний промінь

Потім ми беремо суму і різницю (тобто «дельту») цих двох променів у цифровому вигляді, що означає необхідність використання двох цифрових каналів Phaser, роблячи цей підхід гібридною решіткою (хоча суму та різницю цілком можна виконати й в аналоговому домені за допомогою власного обладнання). Сумарний промінь відповідає променю, центр якого знаходиться у поточній оцінці кута приходу, як показано вище, тобто цей промінь можна використовувати для демодуляції/декодування потрібного сигналу. Дельта-промінь, як ми його називатимемо, важче уявити, але він матиме нуль у точці оціненого кута приходу. Ми можемо використовувати відношення між сумарним променем і дельтою (воно ж помилка), щоб виконувати відстеження. Цей процес найпростіше пояснити коротким фрагментом Python; згадайте, що функція rx() повертає пакет відліків з обох каналів, тож у коді нижче data[0] — це перший канал Pluto (перша група з чотирьох елементів Phaser), а data[1] — другий канал (друга група з чотирьох елементів). Щоб створити два промені, ми будемо окремо керувати кожною з двох груп. Суму, дельту та помилку можна обчислити так:

data = phaser.sdr.rx()
sum_beam = data[0] + data[1]
delta_beam = data[0] - data[1]
error = np.mean(np.real(delta_beam / sum_beam))

Знак помилки підказує, з якого боку насправді надходить сигнал, а її величина вказує, наскільки далеко ми промахнулися. Ми можемо використати цю інформацію, щоб оновити оцінку кута приходу та ваги. Повторюючи цей процес у реальному часі, ми можемо відстежувати сигнал.

Легше зрозуміти, чому це працює, якщо пригадати, що зсув фази на 180 градусів еквівалентний множенню на -1, тож дельта-промінь по суті є сумою першого променя з другою групою, зсуненою на 180 градусів. Якщо сигнал переважно у другому промені, то він матиме зсув фази 180 градусів порівняно з сигналом, отриманим сумарним променем. Також пам’ятайте, що при діленні двох комплексних чисел береться відношення їхніх амплітуд і різниця фаз. Тож якщо сигнал переважно у другому промені, помилка буде від’ємною, а її величина буде пропорційною тому, наскільки сигнал у другому промені домінує над першим.

Тепер перейдемо до повного прикладу на Python. Ми почнемо з копіювання коду, який використовували раніше для розгортки на 180 градусів. Єдине, що додамо, — витягнемо фазу, за якої отримана максимальна потужність:

# Одноразово розгортаємо фазу, щоб отримати початкову оцінку кута приходу (за кодом вище)
# ...
current_phase = phase_angles[np.argmax(powers)]
print("max_phase:", current_phase)

Далі ми створимо два промені: спробуємо на 5 градусів нижче та на 5 градусів вище від поточної оцінки (зверніть увагу, що це в одиницях фази, а не кута, хоча ці величини подібні). Наступний код по суті складається з двох копій попереднього коду для встановлення фазових шифтерів кожного каналу, за винятком того, що перші 4 елементи використовуються для нижнього променя, а останні 4 — для верхнього:

# Створюємо два промені по обидва боки від поточної оцінки
phase_offset = np.radians(5) # СПРОБУЙТЕ ЗМІНИТИ ЦЕ — задайте зміщення від центру в градусах
phase_lower = current_phase - phase_offset
phase_upper = current_phase + phase_offset
# перші 4 елементи використовуються для нижнього променя
for i in range(0, 4):
   channel_phase = (phase_lower * i + phase_cal[i]) % 360.0
   phaser.elements.get(i + 1).rx_phase = channel_phase
# останні 4 елементи використовуються для верхнього променя
for i in range(4, 8):
   channel_phase = (phase_upper * i + phase_cal[i]) % 360.0
   phaser.elements.get(i + 1).rx_phase = channel_phase
phaser.latch_rx_settings() # застосувати налаштування

Перш ніж виконувати власне відстеження, протестуймо наведений вище код, залишивши ваги променів сталими й рухаючи HB100 ліворуч і праворуч (після завершення ініціалізації для пошуку стартового кута):

print("START MOVING THE HB100 A LITTLE LEFT AND RIGHT")
error_log = []
for i in range(1000):
   data = phaser.sdr.rx() # отримуємо пакет відліків
   sum_beam = data[0] + data[1]
   delta_beam = data[0] - data[1]
   error = np.mean(np.real(delta_beam / sum_beam))
   error_log.append(error)
   print(error)
   time.sleep(0.01)

plt.plot(error_log)
plt.plot([0,len(error_log)], [0,0], 'r--')
plt.xlabel("Час")
plt.ylabel("Помилка")
plt.show()

Відображення функції помилки для монопульсового відстеження без оновлення ваг

У цьому прикладі я рухаю HB100. Спочатку тримаю його нерухомо, поки виконується розгортка на 180 градусів, потім трохи відводжу вправо і рухаю, далі переміщую вліво від початкової точки й також злегка коливаю. Приблизно в момент часу 400 на графіку я повертаю його в інший бік і ненадовго утримую там, перш ніж знову трохи помахати. Висновок полягає в тому, що чим далі HB100 від стартового кута, тим більшою стає помилка, а знак помилки показує, з якого боку від стартового кута знаходиться HB100.

Тепер використаємо значення помилки для оновлення ваг. Ми приберемо попередній цикл for і створимо новий цикл, що охоплює весь процес. Для ясності нижче наведено повний приклад коду, за винятком початкової частини з розгорткою на 180 градусів:

# Одноразово розгортаємо фазу, щоб отримати початкову оцінку кута приходу
# ...
current_phase = phase_angles[np.argmax(powers)]
print("max_phase:", current_phase)

# Тепер оновлюємо current_phase на основі помилки
print("START MOVING THE HB100 A LITTLE LEFT AND RIGHT")
phase_log = []
error_log = []
for ii in range(500):
   # Створюємо два промені по обидва боки від поточної оцінки з заданим зсувом
   phase_offset = np.radians(5)
   phase_lower = current_phase - phase_offset
   phase_upper = current_phase + phase_offset
   # перші 4 елементи використовуються для нижнього променя
   for i in range(0, 4):
         channel_phase = (phase_lower * i + phase_cal[i]) % 360.0
         phaser.elements.get(i + 1).rx_phase = channel_phase
   # останні 4 елементи використовуються для верхнього променя
   for i in range(4, 8):
         channel_phase = (phase_upper * i + phase_cal[i]) % 360.0
         phaser.elements.get(i + 1).rx_phase = channel_phase
   phaser.latch_rx_settings() # застосувати налаштування

   data = phaser.sdr.rx() # отримуємо пакет відліків
   sum_beam = data[0] + data[1]
   delta_beam = data[0] - data[1]
   error = np.mean(np.real(delta_beam / sum_beam))
   error_log.append(error)
   print(error)

   # Оновлюємо оцінений кут приходу на основі помилки
   current_phase += -10 * error # підібрано вручну, щоб система відстежувала з приємною швидкістю
   steer_angle = np.degrees(np.arcsin(max(min(1, (3e8 * np.radians(current_phase)) / (2 * np.pi * signal_freq * phaser.element_spacing)), -1)))
   phase_log.append(steer_angle) # приємніше будувати графік за кутом, а не за фазою

   time.sleep(0.01)

fig, [ax0, ax1] = plt.subplots(2, 1, figsize=(8, 10))

ax0.plot(phase_log)
ax0.plot([0,len(phase_log)], [0,0], 'r--')
ax0.set_xlabel("Час")
ax0.set_ylabel("Оцінка фази [градуси]")

ax1.plot(error_log)
ax1.plot([0,len(error_log)], [0,0], 'r--')
ax1.set_xlabel("Час")
ax1.set_ylabel("Помилка")

plt.show()

Демонстрація монопульсового відстеження з Phaser і HB100, який рухають перед ним

Ви можете побачити, що помилка по суті є похідною від оцінки фази; оскільки відстеження працює, оцінка фази загалом відповідає реальному куту приходу. Це не дуже очевидно лише з цих графіків, але коли відбувається різка зміна, системі потрібна невелика частка секунди, щоб підлаштуватися й наздогнати. Мета полягає в тому, щоб зміна кута приходу ніколи не була настільки швидкою, аби сигнал виходив за межі головних пелюсток двох променів.

Набагато легше візуалізувати цей процес, коли решітка лише одновимірна, але практичні випадки застосування монопульсового відстеження майже завжди двовимірні (використовується площинна/2D-решітка замість лінійної, як у Phaser). Для 2D-випадку створюються чотири промені замість двох, і після обробки маємо один сумарний промінь і чотири дельта-промені для керування в обох вимірах.

Радар із Phaser¶

Скоро буде!

Висновок¶

Увесь код, використаний для створення ілюстрацій у цьому розділі, доступний на сторінці підручника в GitHub.