2. Частотна область

Ця глава знайомить з частотною областю і охоплює ряди Фур’є, перетворення Фур’є, властивості Фур’є, ШПФ, вікна і спектрограми, використовуючи приклади на Python.

Одним з найцікавіших побічних ефектів вивчення DSP і бездротового зв’язку є те, що ви також навчитеся мислити в частотній області. Досвід “роботи” в частотній області для більшості людей обмежується регулюванням низьких/середніх/високих частот в автомобільній аудіосистемі. А “перегляд” чогось в частотній області для більшості людей обмежується переглядом динамічного звукового спектра еквалайзера, як на анімації приведеній нижче:

Наприкінці цього розділу ви зрозумієте, що насправді означає частотна область, як перетворювати часову в частотну область і навпаки (а також що при цьому відбувається), і деякі цікаві принципи, які ми будемо використовувати під час вивчення ЦОС (DSP) і ПКР (SDR). До кінця цього підручника ви гарантовано станете майстром у роботі з частотною областю!

По-перше, розберемось чому нам подобається розглядати сигнали в частотній області? Ось два приклади сигналів, показаних як в часовій, так і в частотній області.

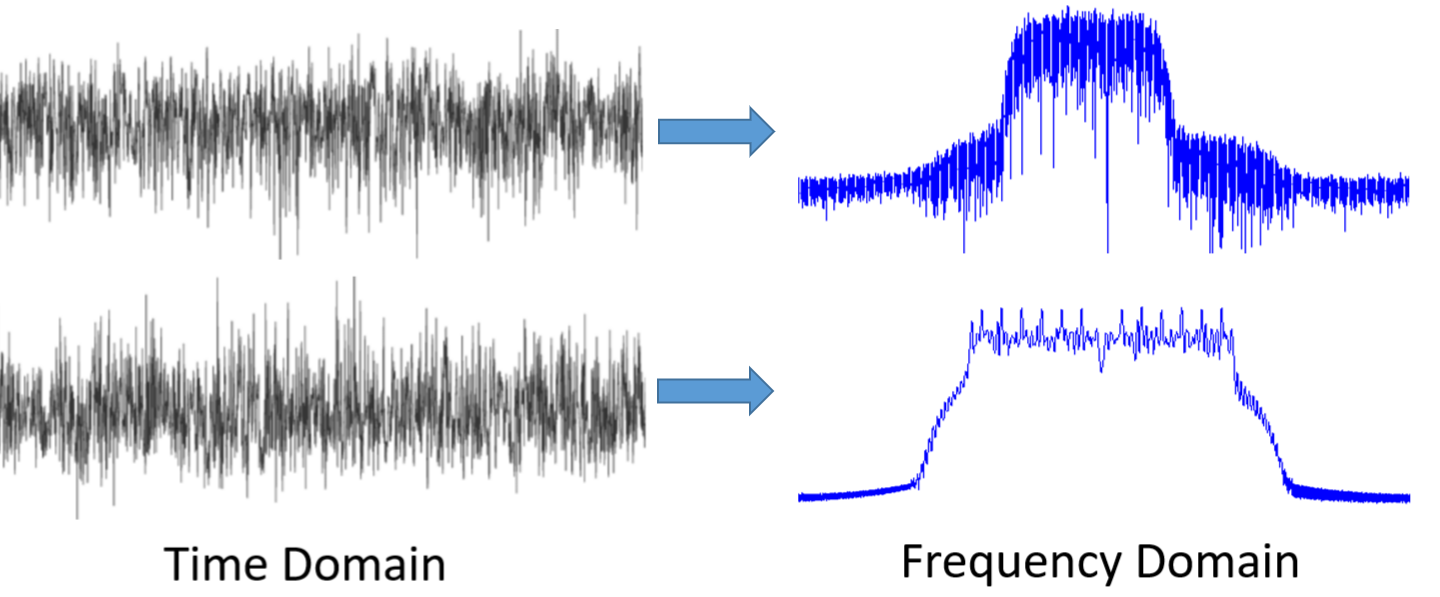
Як ви можете бачити, в часовій області обидва сигнали виглядають як шум, але в частотній області ми бачимо різні особливості. В природі все знаходиться в часовій області; коли ми робимо оцифровку сигналів, ми робимо їх в часовій області, тому що ми не можемо безпосередньо зробити оцифровку сигналу в частотній області. Але найцікавіші речі зазвичай відбуваються саме в частотній області.

Ряди Фур’є

Основи для розуміння частотної області починається з того, що будь-який сигнал може бути представлений, як сума синусоїдальних хвиль. Коли ми розкладаємо сигнал на складові синусоїди, ми називаємо це рядом Фур’є. Ось приклад сигналу, який складається лише з двох синусоїд:

Ось ще один приклад: червона крива нижче апроксимує пилкоподібну хвилю сумою 10 синусоїд. Ми бачимо, що це дає не ідеальне наближення - для відтворення цієї пилкоподібної хвилі знадобилася б нескінченна кількість синусоїд через те, що пилкоподібний сигнал має різкі стрибки:

Деякі сигнали вимагають більше синусоїд, ніж інші, а деякі вимагають нескінченної кількості, хоча і їх завжди можна апроксимувати скінченою кількістю синусоїд. Ось ще один приклад розбиття сигналу на серію синусоїд:

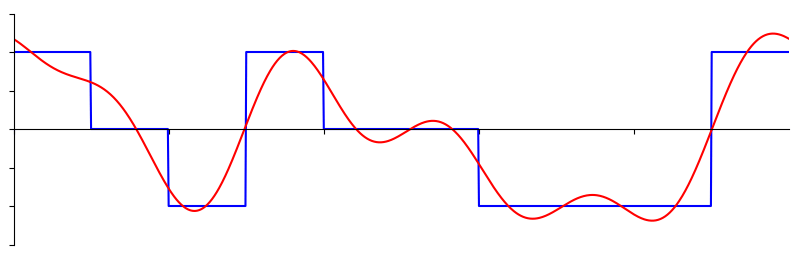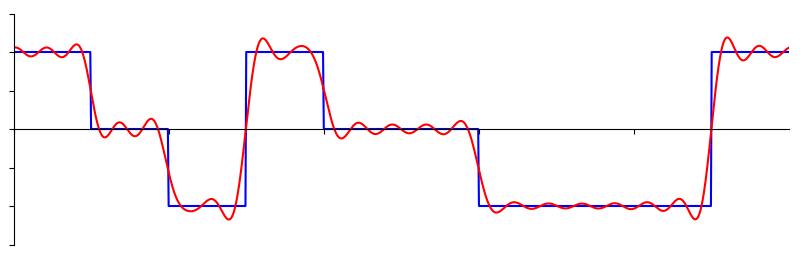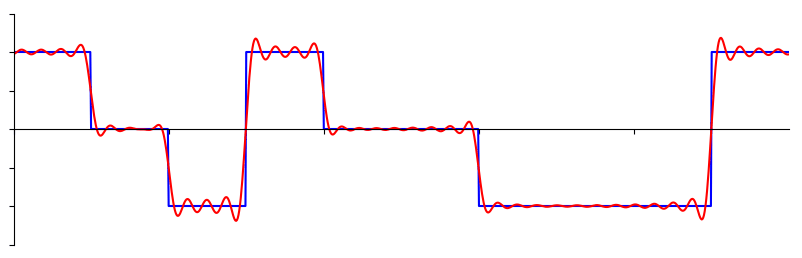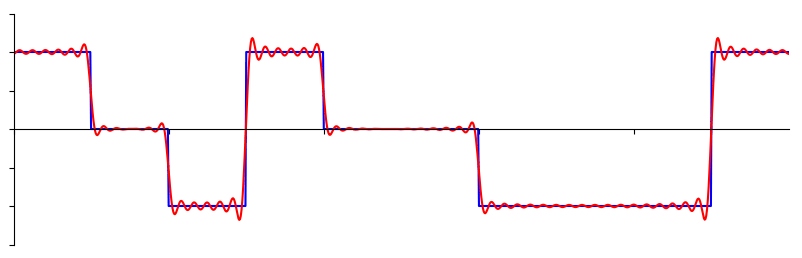
Щоб зрозуміти, як можна розкласти сигнал на синусоїдальні хвилі, або синусоїди, нам потрібно спочатку розглянути три властивості синусоїди:

1. Амплітуда
2. Частота
3. Фаза

Амплітуда вказує на “силу” хвилі, тоді як частота - це кількість хвиль в секунду. Фаза використовується для представлення того, як синусоїда зсунута у часі, в межах від 0 до 360 градусів (або від 0 до \(2\pi\)), але фаза відносне значення, тобто щоб мати якесь значення фаза повинна бути виміряна відносно чогось. Наприклад, два сигнали з однаковою частотою можуть бути зсунуті на 30 градусів відносно один одного.

Тепер ви зрозуміли, що “сигнал” - це, по суті, просто функція, зазвичай представлена “в часі” (тобто на осі х). Іншою її властивісттю, яку легко запам’ятати, є період, який є оберненою величиною до частоти. Період синусоїди - це кількість часу в секундах, за який хвиля завершує один цикл. Таким чином, одиницею частоти є 1/секунда, або Гц.

Коли ми розкладаємо сигнал на суму синусоїд, кожна з них матиме певну амплітуду, фазу і частоту. Амплітуда кожної синусоїди покаже нам, наскільки є сильною складова частоти у сигналі. Не хвилюйтеся надто про фазу поки що, окрім усвідомлення того, що єдина різниця між sin() і cos() - це фазовий зсув (часовий зсув).

Важливіше зрозуміти концепцію, що лежить в основі, ніж самі рівняння, які потрібно розв’язати для отримання ряду Фур’є, але для тих, хто цікавиться рівняннями, я відсилаю вас до стислого пояснення Вольфрама: https://mathworld.wolfram.com/FourierSeries.html.

Часово-частотні пари

Ми з’ясували, що сигнали можуть бути представлені у вигляді синусоїд, які мають декілька властивостей. Тепер давайте навчимося будувати графіки сигналів у частотній області. У той час як часова область демонструє, як сигнал змінюється з часом, частотна область показує, яка частина сигналу на яких частотах знаходиться. Замість того, щоб по осі абсцис відкладати час, ми будемо відкладати частоту. Ми можемо побудувати графік заданого сигналу як по часу, так і по частоті. Для початку розглянемо кілька простих прикладів.

Ось як виглядає синусоїда з частотою f в часовій і частотній області:

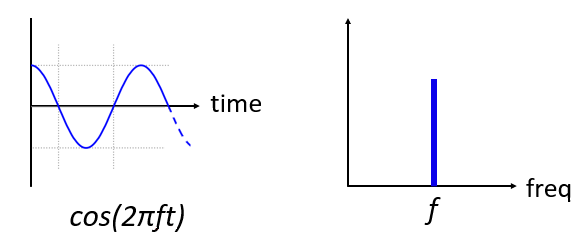
Часова область має виглядати дуже знайомо. Це коливальна функція. Не турбуйтеся про те, в якій точці періоду вона починається або як довго триває. Суть в тому, що сигнал має єдину частоту, тому в частотній області ми бачимо один пік. На якій би частоті не коливалася ця синусоїда, ми побачимо пік у частотній області. Математична назва такого піку називається “імпульс”.

А що, якби ми мали імпульс у часовій області? Уявіть собі звукозапис від хлопавки або удару молотка по цвяху. Ця пара перетвореня з час в частоту трохи менш інтуїтивно зрозуміла.

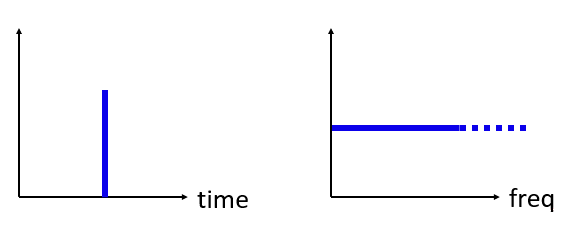
Як ми бачимо, пік/імпульс у часовій області є пласким у частотній області, і теоретично він містить кожну частоту. Теоретично ідеального імпульсу не існує, оскільки він мав би бути нескінченно коротким у часовій області. Як і у випадку з синусоїдою, не має значення, де в часовій області відбувається імпульс. Важливим висновком тут є те, що швидкі зміни в часовій області призводять до виникнення багатьох частот.

Далі давайте подивимося на часові та частотні діаграми прямокутної хвилі:

Цей графік також менш інтуїтивно зрозумілий, але ми бачимо, що в частотній області є сильний пік, який знаходиться на частоті прямокутної хвилі, але з підвищенням частоти піків стає більше. Це пов’язано зі швидкою зміною часової області, як і в попередньому прикладі. Але частота не рівномірна. Вона має піки через певні проміжки часу, і рівень повільно спадає (хоча ніколи теоритично не спадає до 0). Прямокутна хвиля в часовій області в частотній області буде мати вигляд sin(x)/x (так звана sinc-функція).

А що, якщо у нас є постійний сигнал у часовій області? Тоді постійний сигнал не має ніякої “частоти”. Тобто графік буде наступний:

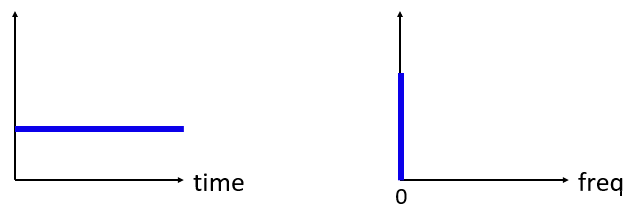
Оскільки частота відсутня, у частотній області ми маємо імпульс на частоті 0 Гц. Це має фізичний сенс, якщо добре подумати про це. Частотна область не може бути “порожньою”, тому що це відбувається лише тоді, коли немає зовсім сигналу (тобто, у часової області 0). Назавемо сигнал з частотою 0 Гц у частотній області “постійним струмом”, тому що він викликаний сигналом постійного струму в часі (тобто постійним сигналом, який не змінюється). Зауважте, що якщо ми збільшимо амплітуду нашого постійного сигналу в часовій області, імпульс на 0 Гц в частотній області також збільшиться.

Пізніше ми дізнаємося, які велечини відкладаються по вісі ординат графіку в частотній області, але поки що ви можете думати про ці велечини як про своєрідну амплітуду, частотних складових присутніх в сигналі в часовій області.

Перетворення Фур’є

Математично “перетворення”, яке ми використовуємо для переходу з часової області в частотну і навпаки, називається перетворенням Фур’є. Воно визначається наступним чином:

\[X(f) = \int x(t) e^{-j2\pi ft} dt\]

Для сигналу x(t) ми можемо отримати частотну версію X(f), використовуючи цю формулу. Ми будемо позначати часову версію функції через x(t) або y(t), а відповідну частотну версію через X(f) та Y(f). Зверніть увагу, що “t” означає час, а “f” - частоту. “j” - це просто уявна одиниця. Ви могли бачити її як “i” на уроках математики в середній школі. Ми використовуємо “j” в інженерії та комп’ютерних науках, тому що “i” часто позначає струм, а в програмуванні часто використовується як ітератор.

Зворотнє перетворенння з частотної в часову область відбувається майже так само, за винятком масштабного коефіцієнта та зміни знаку степені:

\[x(t) = \frac{1}{2 \pi} \int X(f) e^{j2\pi ft} df\]

Зверніть увагу, що у багатьох підручниках та інших джерелах замість \(w\) використовується \(2\pi f\). \(w\) - кутова частота у радіанах за секунду, тоді як \(f\) - у Гц. Все, що вам потрібно знати, це те, що

\[\omega = 2 \pi f\]

Хоча це додає член \(2 \pi\) до багатьох рівнянь, простіше дотримуватися частоти у Гц. Зрештою, ви будете працювати з Гц у вашіх SDR та RF програмних застосунках.

Наведене вище рівняння для перетворення Фур’є є у неперервній формі, яку ви побачите лише у математичних задачах. Дискретна форма цієї формули набагато ближча до того, що реалізується у коді:

\[X_k = \sum_{n=0}^{N-1} x_n e^{-\frac{j2\pi}{N}kn}\]

Зауважте, що основна відмінність полягає у тому, що ми замінили інтеграл на суму. Індекс \(k\) змінюється від 0 до N-1.

Нічого страшного, якщо жодне з цих рівнянь не має для вас особливого значення. Насправді нам не потрібно використовувати їх безпосередньо, щоб робити круті речі з DSP і SDR!

Часо-частотні властивості

Вище ми розглянули приклади того, як сигнали представляються в часовій і частотній областях. Зараз ми розглянемо п’ять важливих “властивостей Фур’є”. Це властивості вказують нам, що якщо ми зробимо ____ з нашим сигналом у часовій області, то ____ станеться з цим сигналом у частотній області. Це дасть нам важливе розуміння типів цифрової обробки сигналів (ЦОС), які ми будемо виконувати з сигналами у часовій області на практиці.

1. Властивість лінійності:

\[a x(t) + b y(t) \leftrightarrow a X(f) + b Y(f)\]

Ця властивість, мабуть, найпростіша для розуміння. Якщо ми додаємо два сигнали в часі, то частотна версія також буде двома частотними сигналами, доданими разом. Вона також говорить нам, що якщо ми помножимо будь-який з них на коефіцієнт масштабування, частотна область також масштабуватиметься на ту саму величину. Корисність цієї властивості стане більш очевидною, коли ми додамо разом кілька сигналів.

2. Властивість зсуву частоти:

\[e^{2 \pi j f_0 t}x(t) \leftrightarrow X(f-f_0)\]

Член зліва від x(t) - це те, що ми називаємо “комплексною синусоїдою” або “комплексною експонентою”. Наразі, все, що нам потрібно знати, це те, що по суті це просто синусоїда з частотою \(f_0\). Ця властивість говорить нам, що якщо ми візьмемо сигнал \(x(t)\) і помножимо його на синусоїду, то у частотній області ми отримаємо \(X(f)\), тільки зсунутий на певну частоту, \(f_0\). Цей зсув частоти може бути легше візуалізувати:

Зсув частоти є невід’ємною властивістю ЦОС, оскільки з багатьох причин нам може знадобитися зсув сигналів вгору або вниз по частоті. Ця властивість показує нам, як це зробити (помножити на синусоїду). Ось ще один спосіб візуалізувати цю властивість:

3. Масштабування у властивості Time:

\[x(at) \leftrightarrow X\left(\frac{f}{a}\right)\]

У лівій частині рівняння ми бачимо, що ми масштабуємо наш сигнал x(t) у часовій області. Ось приклад масштабування сигналу в часі, а потім те, що відбувається з частотними версіями кожного з них.

Масштабування в часі, по суті, стискає або розширює сигнал по осі x. Ця властивість говорить нам про те, що масштабування в часовій області спричиняє зворотне масштабування в частотній області. Наприклад, коли ми передаємо біти швидше, ми повинні використовувати більшу пропускну здатність. Ця властивість допомагає пояснити, чому сигнали з вищою швидкістю передачі даних займають більшу смугу пропускання/спектр. Якби масштабування час-частота було пропорційним, а не обернено пропорційним, оператори стільникового зв’язку могли б передавати стільки біт в секунду, скільки вони хочуть, не платячи мільярди за спектр! На жаль, це не так.

Ті, хто вже знайомий з цією властивістю, можуть помітити відсутність масштабного коефіцієнта; він не враховується заради простоти. Для практичних цілей це не має значення.

4. Згортка по часу:

\[\int x(\tau) y(t-\tau) d\tau \leftrightarrow X(f)Y(f)\]

Вона називається згорткою по часу, тому що у часовій області ми згортаємо x(t) та y(t). Можливо, ви ще не знаєте про операцію згортки, тому поки уявіть її як крос-кореляцію, адже ми зануримося у згортки глибше у цьому розділі. Коли ми згортаємо часові сигнали, це еквівалентно перемноженню частотних версій цих двох сигналів. Це дуже відрізняється від додавання двох сигналів. Коли ви додаєте два сигнали, як ми бачили, нічого насправді не відбувається, ви просто додаєте частотні версії. Але коли ви згортаєте два сигнали, ви ніби створюєте з них новий третій сигнал. Згортка - це найважливіша техніка в ЦОС, але для того, щоб повністю її зрозуміти, ми повинні спочатку зрозуміти, як працюють фільтри.

Перш ніж ми продовжимо, щоб коротко пояснити, чому ця властивість настільки важлива, розглянемо таку ситуацію: у вас є один сигнал, який ви хочете отримати, і поруч з ним є сигнал, що заважає.

Концепція маскування широко використовується у програмуванні, тому давайте використаємо її тут. Що, якби ми могли створити маску наведену на рисунку нижче і помножити її на сигнал наведений вище, щоб замаскувати той, який нам не потрібен?

Зазвичай ми виконуємо операції ЦОС у часовій області, тому давайте скористаємося властивістю згортки, щоб побачити, як ми можемо зробити це маскування у часовій області. Скажімо, що x(t) - це отриманий сигнал. Нехай Y(f) - це маска, яку ми хочемо застосувати у частотній області. Це означає, що y(t) є часовим представленням нашої маски, і якщо ми згорнемо її з x(t), ми зможемо “відфільтрувати” небажаний сигнал.

Коли ми будемо обговорювати фільтрацію, згортки матимуть більше сенсу.

5. Згортка по частоті:

Насамкінець, я хочу зазначити, що властивість згортки працює і у зворотному напрямку, хоча ми не будемо використовувати її так часто, як властивість згортки у часовій області:

\[x(t)y(t) \leftrightarrow \int X(g) Y(f-g) dg\]

Існують і інші властивості, але наведені вище п’ять, на мою думку, є найбільш важливими для розуміння. Навіть якщо ми не довели кожну з них, суть в тому, що ми використовуємо математичні властивості, щоб розуміти, що відбувається з реальними сигналами при аналізі та обробці. Не зациклюйтеся на рівняннях. Переконайтеся, що ви розумієте опис кожної властивості.

Швидке перетворення Фур’є (ШПФ)

Тепер повернемося до перетворення Фур’є. Я показав вам рівняння для дискретного перетворення Фур’є, але 99.9% часу ви будете використовувати під час кодування функцію ШПФ, fft(). Швидке перетворення Фур’є (ШПФ) - це просто алгоритм для обчислення дискретного перетворення Фур’є. Його було розроблено десятки років тому, і хоча існують різні варіанти реалізації, він все ще залишається лідером з обчислення дискретного перетворення Фур’є. Нам пощастило, що вони назвали його “швидким”.

ШПФ - це функція з одним входом і одним виходом. Вона перетворює сигнал з часу в частоту:

У цьому підручнику ми розглядатимемо лише одновимірні ШПФ (двовимірні використовуються для обробки зображень та інших застосувань). Для наших цілей вважатимемо, що функція ШПФ має один вхід: вектор відліків, і один вихід: частотну версію цього вектора відліків. Розмір виходу завжди дорівнює розміру входу. Якщо я подам на вхід ШПФ 1,024 відліки, я отримаю 1,024 на виході. Складність полягає в тому, що результат завжди буде в частотній області, а отже, “розмах” осі х, якщо ми побудуємо графік, не зміниться залежно від кількості відліків на вході в часовій області. Давайте візуалізуємо це, подивившись на вхідні та вихідні масиви разом з одиницями виміру їхніх індексів:

Оскільки вихідні дані знаходяться в частотній області, значення діапазону по осі х залежить від частоти дискретизації, яку ми розглянемо в наступній главі. Коли ми використовуємо більше відліків для вхідного вектора, ми отримуємо кращу роздільну здатність у частотній області (як додаток до обробки більшої кількості відліків за один раз). Насправді ми не “бачимо” більше частот, маючи довший вхідний сигнал. Єдиний спосіб збільшити кількість частот - збільшити частоту дискретизації (зменшити період дискретизації \(\Delta t\)).

Як нам насправді відобразити цей вихідний результат ШПФ? Для прикладу припустимо, що наша частота дискретизації становить 1 мільйон відліків за секунду (1 МГц). Як ми дізнаємося з наступного розділу, це означає, що ми можемо бачити тільки сигнали з частотою до 0,5 МГц, незалежно від того, скільки відліків ми подаємо на ШПФ. Вихідні дані ШПФ можна представити наступним чином:

Це завжди так; на виході ШПФ завжди будуть значення від \(\text{-} f_s/2\) до \(f_s/2\), де \(f_s\) - частота дискретизації. Тобто на виході завжди буде від’ємна частина і додатна частина. Якщо вхідний сигнал комплексний, то від’ємна і додатна частини будуть відрізнятися, але якщо він дійсний, то вони будуть ідентичні.

Щодо частотного інтервалу, то кожен відлік відповідає \(f_s/N\) Гц, тобто подача більшої кількості відліків на кожне ШПФ призведе до більш деталізованої роздільної здатності на виході. Дуже незначна деталь, яку можна проігнорувати, якщо ви новачок: математично останній індекс не відповідає точно \(f_s/2\), скоріше це \(f_s/2 - f_s/N\), що для великого \(N\) буде приблизно дорівнювати \(f_s/2\).

Від’ємні частоти

Що таке від’ємна частота? Наразі просто вважайте, що це пов’язано з використанням комплексних чисел (уявних чисел) - насправді не існує такого поняття, як “від’ємна частота”, коли мова йде про передачу/прийом радіосигналів, це просто представлення, яке ми використовуємо. Можно думати про це наступним чином. Уявімо, що ми говоримо нашому SDR налаштуватися на частоту 100 МГц (FM-діапазон) і робити оцифровку з частотою дискритизації 10 МГц. Іншими словами, ми будемо бачити спектр від 95 МГц до 105 МГц. Незхай в цьому діапазоні присутні три сигнали:

І, коли SDR зробить ШПФ ми отримаємо на виході:

Пам’ятайте, що ми налаштували SDR на 100 МГц. Отже, сигнал, який був на частоті близько 97,5 МГц, у цифровому вираженні виглядає як -2,5 МГц, що технічно є від’ємною частотою. Насправді це просто частота, нижча за центральну частоту. Це матиме більше сенсу, коли ми дізнаємося більше про дискретизацію і отримаємо досвід використання наших SDR.

З математичної точки зору, негативні частоти можна уявити наступним чином, розглянемо комплексну експоненціальну функцію \(e^{2j \pi f t}\). Якщо у нас від’ємна частота, то це еквівалентно тому, що в полярних координатах ця комплексна синусоїда обертається у протилежному напрямку.

\[e^{2j \pi f t} = \cos(2 \pi f t) + j \sin(2 \pi f t) \quad \mathrm{\textcolor{blue}{blue}}\]

\[e^{2j \pi (-f) t} = \cos(2 \pi f t) - j \sin(2 \pi f t) \quad \mathrm{\textcolor{red}{red}}\]

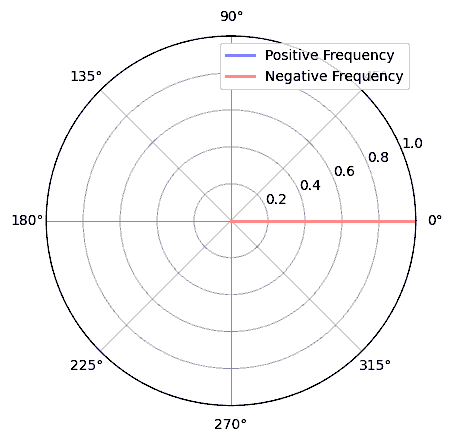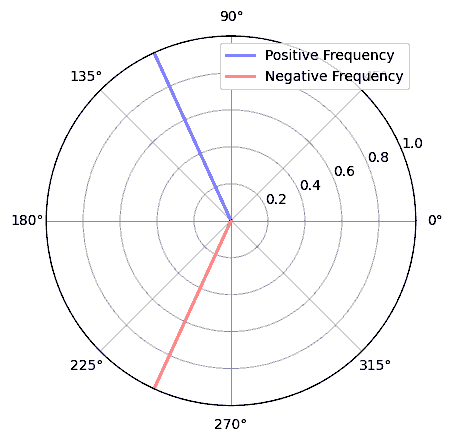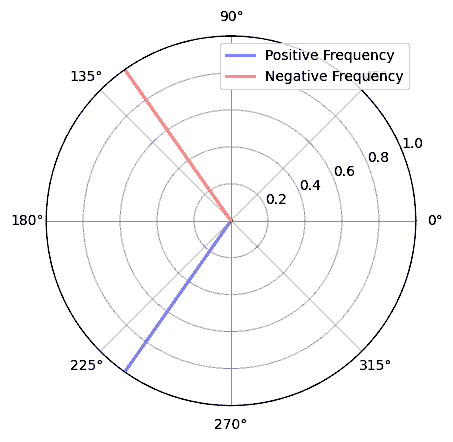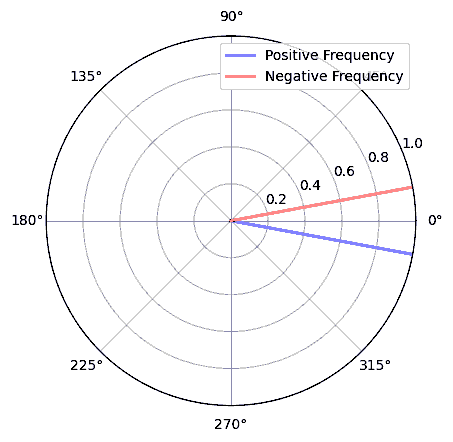
Ми використали комплексну експоненту вище тому, що \(cos()\) або \(sin()\) містить як додатні, так і від’ємні частоти, як видно з формули Ейлера, застосованої до синусоїди на частоті \(f\) з часом \(t\):

\[\cos(2 \pi f t) = \underbrace{\frac{1}{2} e^{2j \pi f t}}_\text{positive} + \underbrace{\frac{1}{2} e^{-2j \pi f t}}_\text{negative}\]

\[\sin(2 \pi f t) = \underbrace{\frac{1}{2j} e^{2j \pi f t}}_\text{positive} - \underbrace{\frac{1}{2j} e^{-2j \pi f t}}_\text{negative}\]

Отже, в обробці радіочастотних сигналів ми зазвичай використовуємо комплексні експоненти замість косинусів і синусів.

Порядок в часі не має значення

Остання властивість перед тим, як ми перейдемо до ШПФ. Функція ШПФ ніби “перемішує” вхідний сигнал так, щоб сформувати вихідний сигнал, який має інший масштаб і одиниці виміру. Після чого, ми більше не перебуваємо в часовій області. Гарний спосіб усвідомити цю різницю між областями - це усвідомити, що зміна порядку подій у часовій області не змінює частотні компоненти сигналу. Тобто, виконання одного ШПФ для приведених нижче на рисунку двох сигналів матиме однакові два піки, оскільки сигнал - це просто дві синусоїди на різних частотах. Зміна порядку виникнення синусоїд не змінює того факту, що це дві синусоїди на різних частотах. Це передбачає, що обидві синусоїди виникають в один і той самий проміжок часу, що подається на ШПФ; якщо скоротити розмір ШПФ та виконати кілька ШПФ (як ми зробимо в розділі “Спектрограма”), то можна розрізнити ці дві синусоїди.

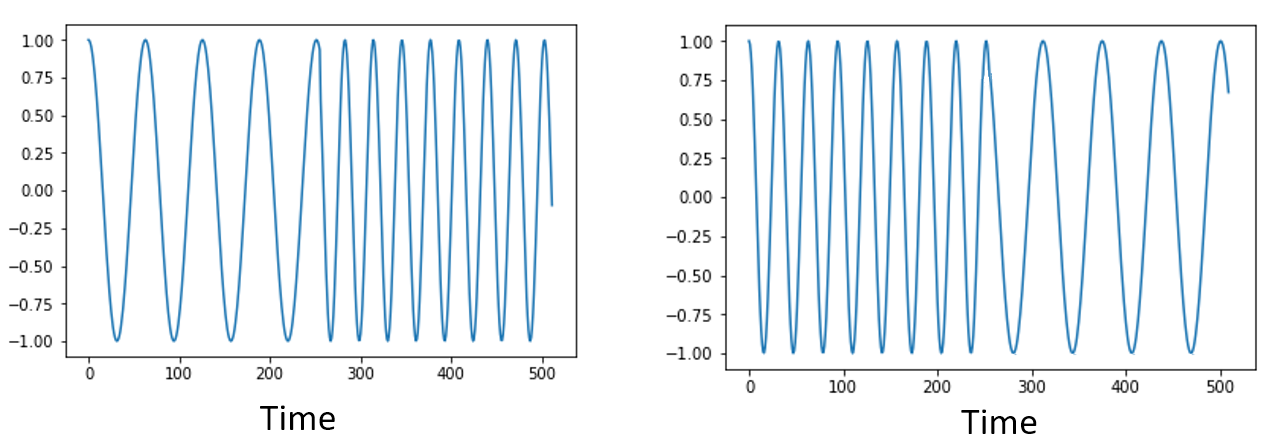
Технічно, фаза значень ШПФ зміниться через часовий зсув синусоїд. Однак у перших кількох розділах цього підручника нас цікавитиме здебільшого амплітудти ШПФ.

ШПФ у Python

Тепер, коли ми дізналися про те, що таке ШПФ і як представляється результат, давайте розглянемо код на Python і скористаємося функцією ШПФ Numpy, np.fft.fft(). Рекомендується використовувати повноцінну консоль/IDE Python на вашому комп’ютері, але в крайньому випадку ви можете скористатися веб-консоллю Python, посилання на яку знаходиться внизу навігаційної панелі зліва.

Спочатку нам потрібно створити сигнал у часовій області. Ви можете скористатися власною консоллю Python для відтворення прикладів. Для спрощення ми створимо просту синусоїду з частотою 0,15 Гц. Ми також будемо використовувати частоту дискретизації 1 Гц, тобто в часі ми будемо робити відліки через 0, 1, 2, 3 секунди і т.д.

import numpy as np
t = np.arange(100)
s = np.sin(0.15*2*np.pi*t)

Якщо ми побудуємо графік s, то він буде виглядати так:

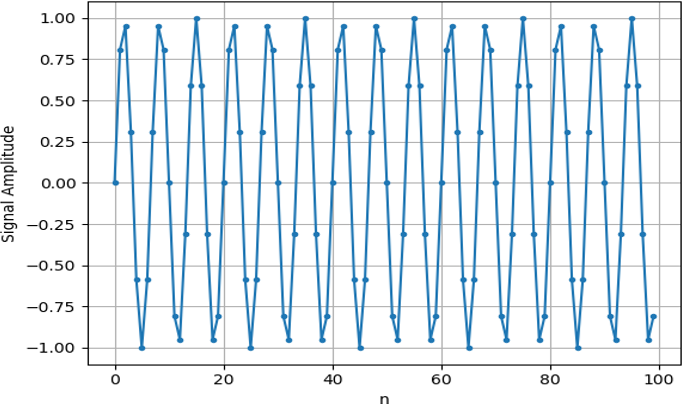
Далі скористаємося функцією ШПФ Numpy:

S = np.fft.fft(s)

Якщо ми подивимось на S, то побачимо, що це масив комплексних чисел:

S = array([-0.01865008 +0.00000000e+00j, -0.01171553 -2.79073782e-01j,0.02526446 -8.82681208e-01j, 3.50536075 -4.71354150e+01j, -0.15045671 +1.31884375e+00j, -0.10769903 +7.10452463e-01j, -0. 09435855 +5.01303240e-01j, -0.08808671 +3.92187956e-01j, -0.08454414 +3.23828386e-01j, -0.08231753 +2.76337148e-01j, -0.08081535 +2.41078885e-01j, -0.07974909 +2.13663710e-01j,.

Порада: незалежно від того, що ви робите, якщо ви зіткнулись з комплексними числами, спробуйте обчислити амплітуду і фазу і подивіться, може це додасть більше розуміння. Давайте так і зробимо, і побудуємо графік амплітуди і фази. У більшості мов для знаходження амплітуди комплексного числа є функція abs(). Функція для фази може бути різною, але у Python це np.angle().

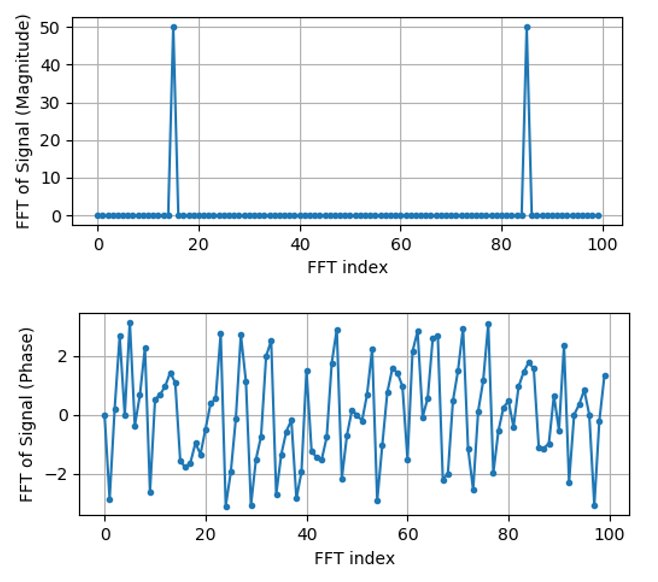
Наразі ми не додаємо розмірності до вісі x для графіків, це лише індекс масиву (що рахується від 0). З математичних міркувань, вихідні дані після ШПФ мають наступний формат:

Але ми хотіли б мати 0 Гц (постійний струм) в центрі і від’ємні частоти зліва (це те як зазвичай ми представляємо графіки). Отже, кожного разу, коли ми робимо ШПФ, нам потрібно виконати “зсув ШПФ”, який є простою операцією перегрупування масиву, на кшталт кільцевого зсуву, але більше схожого на “покладіть це сюди, а це туди”. На наведеній нижче схемі повністю описано, що робить операція зсуву ШПФ:

Для зручності у Numpy є функція зсуву ШПФ, np.fft.fftshift(). Замініть рядок np.fft.fft() на:

S = np.fft.fftshift(np.fft.fft(s))

Нам також потрібно розібратися зі значеннями/мітками по осі x. Пам’ятайте, що ми використовували частоту дискретизації 1 Гц для спрощення. Це означає, що лівий край графіка частотної області буде -0,5 Гц, а правий - 0,5 Гц. Якщо що це поки незрозуміло, то стане зрозуміло після того, як ви прочитаєте розділ Вибірка IQ. Давайте дотримуватися цього припущення, що наша частота дискретизації становить 1 Гц, і побудуємо графік амплітуди і фази вихідного сигналу ШПФ з відповідною міткою на осі абсцис. Ось остаточна версія цього прикладу на Python і результат:

import numpy as np
import matplotlib.pyplot as plt

Fs = 1 # Гц
N = 100 # кількість точок для моделювання та розмір нашого ШПФ

t = np.arange(N) # оскільки наша частота дискретизації 1 Гц
s = np.sin(0.15*2*np.pi*t)
S = np.fft.fftshift(np.fft.fft(s))
S_mag = np.abs(S)
S_phase = np.angle(S)
f = np.arange(Fs/-2, Fs/2, Fs/N)
plt.figure(0)
plt.plot(f, S_mag, '.-')
plt.figure(1)
plt.plot(f, S_phase, '.-')
plt.show()

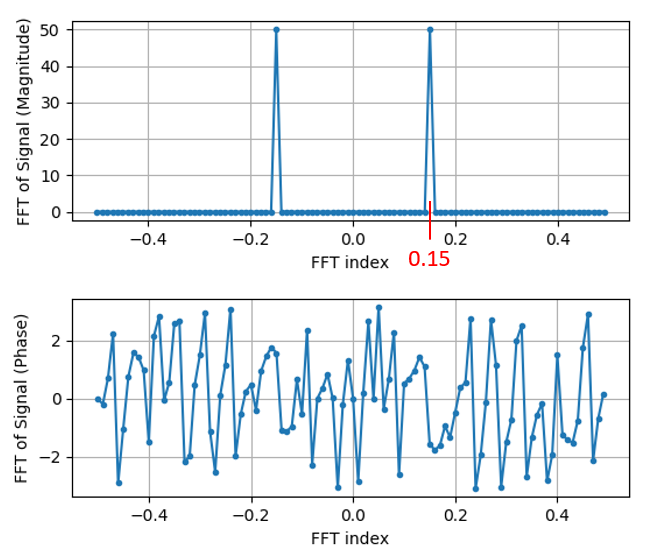
Зверніть увагу, що ми бачимо наш пік на частоті 0.15 Гц, тобто на частоті, яку ми використовували при створенні синусоїди. Це означає, що наше ШПФ спрацювало! Якби ми не знали коду, який використовувався для генерації синусоїди, а нам просто дали список зразків, ми могли б використати ШПФ для визначення частоти. Причина, чому ми бачимо пік на частоті -0,15 Гц, пов’язана з тим, що це був дійсний , а не комплексний сигнал, і цей випадок ми глибше розглянемо пізніше.

Віконна функція

Коли ми використовуємо ШПФ для вимірювання частотних складових нашого сигналу, ми припускаємо, що ШПФ обробляє тільки фрагмент періодичного сигналу. Тобто результат ШПФ на фрагментом такий, ніби поданий сигналу продовжується далі повторюватися до нескінченності. Тобто останній відлік фрагменту має з’єднуватися з першим відліком наступного фрагменту, але так як фрагмент циклічно повторюються - то це ж і є першим відліком нашого фрагменту. Це випливає з теорії, що лежить в основі перетворення Фур’є. Це для нас означає, що ми не хочемо різкіх перепадів амплітуди між цим останім і першим відліком, бо різкі перепади в часовій області приведуть в частотній області до виникнення багатьох додаткових частот, але насправді для довільного сигналу наш останній і перший відлік можуть не так плавно з’єднуватись. Простіше кажучи, якщо ми робимо ШПФ зі 100 відліків, використовуючи np.fft.fft(x), ми хочемо, щоб x[0] і x[99] були рівними або близькими за значенням.

Для того щоб зкомпенсувати цей перепад при циклічному повторенні фрагменту ми використовуємо “віконну функцію”. Безпосередньо перед операцією ШПФ ми множимо фрагмент сигналу на віконну функцію, яка дорівнює довжині фрагменту і може бути будь-якою функцією, що спадає до нуля на обох кінцях. Це гарантує, що фрагмент сигналу буде починатися і закінчуватися в нулі і таким чином плавно з’єднуватися. До поширених віконних функцій належать функції Геммінга, Ганнінга, Блекмана та Кайзера. Якщо ви не застосовуєте жодної віконної функції, це називається використанням “прямокутного” вікна, тому що це еквіввалентно множення фрагменту на масив одиниць. Ось як виглядають деякі віконні функції:

Простим підходом для початківців є використання вікна Гамінга, яке можна створити у Python за допомогою np.hamming(N), де N - це кількість елементів у масиві, що є розміром вашого фрагменту для ШПФ. У наведеній вище вправі ми застосуємо вікно безпосередньо перед ШПФ. Після 2-го рядка в коді ми б вставили

s = s * np.hamming(100)

Якщо ви боїтеся обрати неправильне вікно, не бійтеся. При викорстані різниця між Hamming, Hanning, Blackman і Kaiser вікнами дуже мінімальна у порівнянні з тем ефектом, що буде якщо взагалі їх не використати, оскільки всі вони знижують значання фамплітуд фрагментів до нуля з обох боків і вирішують основну проблему плавного з’єднання.

Визначення розміру ШПФ

Останнє, на що слід звернути увагу - це розмір ШПФ. Через спосіб реалізації алгоритму ШПФ - найкращий розмір фрагменту сигналу ШПФ завжди має дорівнювати числу, що є порядоком 2. Ви можете використовувати розмір, який не є порядком 2, але при цьому алгоритм буде працювати повільніше. Найпоширеніші розміри виборки сигналу - від 128 до 4096, хоча, звичайно, можно використовувати і вибіркі більшого розміру. На практиці нам, можливо, доведеться обробляти сигнали довжиною в мільйони або мільярди відліків, тому нам потрібно розбити сигнал на фрагменти і виконати над ними багато операцій ШПФ. Це означає, що ми отримаємо багато результатів ШПФ. Далі ми можемо або усереднити їх, або будувати графік частот що змінюється з часом (це особливо зручно якщо наш сигнал змінюється з часом). Вам не обов’язково пропускати через ШПФ кожний відлік сигналу, щоб отримати гарне представлення цього сигналу в частотній області. Наприклад, ви можете застосувати ШПФ лише до 1,024 з кожних 100 тис. відліків сигналу, і отримані частоти, ймовірно, будуть добре відповідати спектру, якщо ви маєте непреривний сигнал.

Спектрограма/Водоспад

Спектрограма - це графік, який показує зміну амлітуд частот з часом. Це просто набір результатів ШПФ, складений разом (по вертикалі, якщо вам потрібна частота на горизонтальній осі). Ми також можемо показати його в реальному часі, часто його називають водоспадом. Аналізатор спектру - це прилад, який показує цю спектрограму/водоспад. На схемі нижче показано, як розділяють масив відліків IQ на зрізи так, щоб сформувати спектрограму:

Оскільки спектрограма передбачає побудову двовимірних даних від часу то, вона фактично є тривимірним графіком, і щоб представити ці значення частот від часу на двовимірному графіку нам треба додатково використати кольорову карту. Нижче наведений приклад спектрограми, з частотою по горизонтальній осі Х і часом по вертикальній осі Y. Синій колір відповідає найнижчому рівню енергії, а червоний - найвищому. Ми бачимо, що в центрі графіку є сильний пік амплітуди постійного струму (0 Гц) навколо якого є змінні частоти. Синій колір представляє наш рівень шуму.

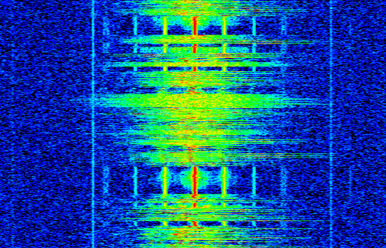
Пам’ятайте, що це просто ШПФ від зрізів з нашого сигналу, накладені один на одного, кожен ряд - це одна операція ШПФ над фрагментом (технічно, амплітуди частот отримані після ШПФ). Тому не забудьте розбити вхідний сигнал на зрізи, розмір яких дорівнює розміру вашого ШПФ (наприклад, 1024 відліків на зріз). Перш ніж перейти до коду для створення спектрограми, наведемо приклад сигналу, який ми будемо використовувати, це просто тон з накладеним на нього білим шумом:

import numpy as np
import matplotlib.pyplot as plt

sample_rate = 1e6

# Згенерувати тон плюс шум
t = np.arange(1024*1000)/sample_rate # вектор часу
f = 50e3 # частота тону
x = np.sin(2*np.pi*f*t) + 0.2*np.random.randn(len(t))

Ось як це виглядає в часовій області (перші 200 відліків):

Ось як з Python ми можемо згенерувати його спектрограму:

# імітуємо сигнал вище, або використовуємо свій власний сигнал

fft_size = 1024
num_rows = len(x) // fft_size # // цілочисельне ділення, яке округлюється вниз
spectrogram = np.zeros((num_rows, fft_size))
for i in range(num_rows):
    spectrogram[i,:] = 10*np.log10(np.abs(np.fft.fftshift(np.fft.fft(x[i*fft_size:(i+1)*fft_size])))**2)

plt.imshow(spectrogram, aspect='auto', extent = [sample_rate/-2/1e6, sample_rate/2/1e6, 0, len(x)/sample_rate])
plt.xlabel("Частота [МГц]")
plt.ylabel("Час [с]")
plt.show()

У результаті ми отримаємо наступну спектрограму, яка не дуже цікава, оскільки немає жодних змін частот у часі. Тут є два тон-сигнали, так як ми моделюємо дійсний сигнал, а дійсні сигнали завжди мають рівні але дзеркально відображені позитивну і негативну частину у своєму спектрі щільності потужності (PSD). Більше цікавих прикладів спектрограм можна знайти на сайті https://www.IQEngine.org!

Реалізація ШПФ

Незважаючи на те, що NumPy вже реалізує ШПФ, корисно знати основи того, як він працює під капотом. Найпопулярнішим алгоритмом ШПФ є алгоритм ШПФ Кулі-Тьюкі, вперше винайдений близько 1805 року Карлом Фрідріхом Гаусом, а потім перевідкритий і популяризований Джеймсом Кулі і Джоном Тьюкі в 1965 році.

Базова версія цього алгоритму працює на виборках розміру степені двійки і призначена для комплексних вхідних даних, але також може працювати і з дійсними вхідними даними. Будівельний блок цього алгоритму відомий як “метелик”, який по суті є ШПФ розміру N = 2, що складається з двох множень і двох підсумовувань:

або

\[ \begin{align}\begin{aligned}y_0 = x_0 + x_1 w^k_N\\y_1 = x_0 - x_1 w^k_N\end{aligned}\end{align} \]

де \(w^k_N = e^{j2\pi k/N}\) це комплексний коефіцієнт обертання (\(N\) - розмір під-шПФ, а \(k\) - індекс). Зауважте, що вхідні та вихідні дані мають бути комплексними, наприклад, \(x_0\) може бути 0.6123 - 0.5213j, і суми/множники є також комплексними.

Алгоритм є рекурсивним і розбивається навпіл, поки не залишиться лише серія метеликів, дивись нижче БПФ розміру 8:

Кожен стовпчик у цьому шаблоні є набором операцій, які можна виконувати паралельно, за \(log_2(N)\) кроків, тому обчислювальна складність ШПФ становить O(\(N\log N\)), тоді як ДПФ - O(\(N^2\)).

Для тих, хто краще розуміє код, ніж рівняння, нижче наведено просту реалізацію ШПФ на Python, а також приклад сигналу, що складається з тону і шуму, на якому можно спробувати цю реалізацію ШПФ.

import numpy as np
import matplotlib.pyplot as plt

def fft(x):
    N = len(x)
    if N == 1:
        return x
    twiddle_factors = np.exp(-2j * np.pi * np.arange(N/2) / N)
    x_even = fft(x[::2]) # ура рекурсії!
    x_odd = fft(x[1::2])
    return np.concatenate([x_even + twiddle_factors * x_odd,
                           x_even - twiddle_factors * x_odd])

# Імітуємо тон + шум
sample_rate = 1e6
f_offset = 0.2e6 # Зсув від несучої на 200 кГц
N = 1024
t = np.arange(N)/sample_rate
s = np.exp(2j*np.pi*f_offset*t)
n = (np.random.randn(N) + 1j*np.random.randn(N))/np.sqrt(2) # одиничний комплексний шум
r = s + n # 0 dB SNR

# Виконати fft, fftshift, перевести в дБ
X = fft(r)
X_shifted = np.roll(X, N/2) # еквівалентно np.fft.fftshift
X_mag = 10*np.log10(np.abs(X_shifted)**2)

# Виведення результатів на екран
f = np.linspace(sample_rate/-2, sample_rate/2, N)/1e6 # plt у МГц
plt.plot(f, X_mag)
plt.plot(f[np.argmax(X_mag)], np.max(X_mag), 'rx') # показати max
plt.grid()
plt.xlabel('Частота [МГц]')
plt.ylabel('Амплітуда [дБ]')
plt.show()

Для тих, хто цікавиться реалізаціями на JavaScript та/або WebAssembly, зверніть увагу на бібліотеку WebFFT для виконання ШПФ у веб- або NodeJS-додатках, вона містить кілька реалізацій, а також інструмент benchmarking tool для порівняння продуктивності кожної реалізації.