8. Шум і дБ¶

У цій главі ми обговоримо шум, включаючи те, як він моделюється і обробляється в системі бездротового зв’язку. Поняття включають AWGN, комплексний шум і SNR/SINR. Ми також познайомимося з децибелами (дБ), оскільки вони широко використовуються в бездротовому зв’язку та SDR.

Гауссівський шум¶

Більшість людей знайомі з поняттям шуму: небажані флуктуації, які можуть затьмарювати бажаний сигнал (сигнали). Шум виглядає приблизно так:

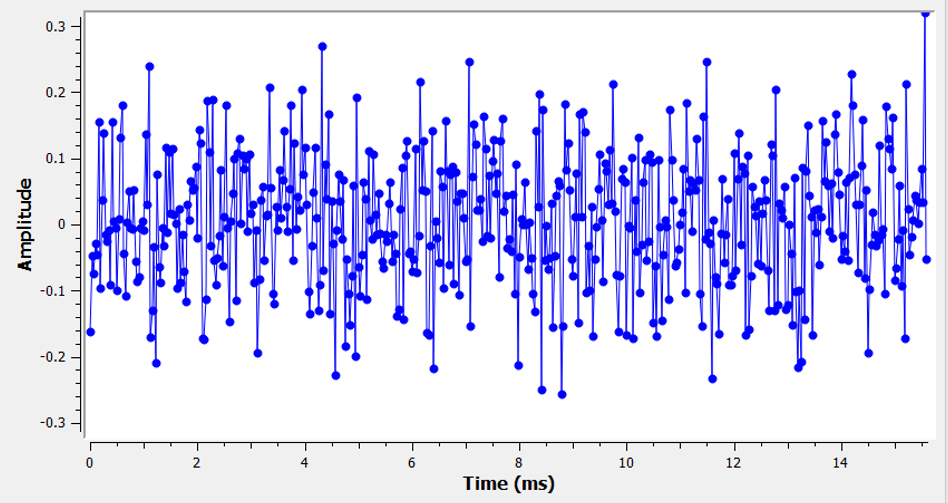
Зверніть увагу, що середнє значення дорівнює нулю на часовому графіку. Якби середнє значення не дорівнювало нулю, то ми могли б відняти середнє значення, назвати його зсувом, і у нас залишилося б середнє значення, що дорівнює нулю. Також зверніть увагу, що окремі точки на графіку не “рівномірно випадкові”, тобто більші значення зустрічаються рідше, більшість точок ближче до нуля.

Ми називаємо цей тип шуму “гаусівським шумом”. Це хороша модель для типу шуму, який походить від багатьох природних джерел, таких як теплові коливання атомів у кремнії радіочастотних компонентів нашого приймача. Теорема про центральну межу говорить нам, що сума багатьох випадкових процесів буде мати гаусівський розподіл, навіть якщо окремі процеси мають інші розподіли. Іншими словами, коли відбувається і накопичується багато випадкових подій, результат виглядає приблизно гауссівським, навіть якщо окремі події не розподілені за гауссівським законом.

Центральна гранична теорема, візуалізована як сума багатьох випадкових процесів, що приводять до нормального розподілу (так званого гауссового розподілу)

Розподіл Гауса також називають “нормальним” розподілом (згадайте криву дзвону).

Розподіл Гауса має два параметри: середнє значення і дисперсію. Ми вже обговорювали, як середнє значення можна вважати нульовим, тому що ви завжди можете вилучити середнє значення, або зміщення, якщо воно не дорівнює нулю. Дисперсія показує, наскільки “сильним” є шум. Вища дисперсія призводить до більших чисел. Саме з цієї причини дисперсія визначає потужність шуму.

Дисперсія дорівнює стандартному відхиленню в квадраті ( $\sigma^2$ ).

Децибели (дБ)¶

Ми зробимо невеликий екскурс, щоб формально ввести дБ. Можливо, ви вже чули про дБ, і якщо ви вже знайомі з ним, можете пропустити цей розділ.

Робота в дБ надзвичайно корисна, коли нам потрібно мати справу з малими і великими числами одночасно, або просто з купою дуже великих чисел. Розглянемо, наскільки громіздкою була б робота з числами шкали в Прикладі 1 і Прикладі 2.

Приклад 1: Сигнал 1 приймається потужністю 2 Вт, а рівень шуму становить 0,0000002 Вт.

Приклад 2: Сміттєпровід працює в 100 000 разів голосніше, ніж у тихій сільській місцевості, а ланцюгова пила в 10 000 разів голосніше, ніж сміттєпровід (з точки зору потужності звукових хвиль).

Без децибел, тобто працюючи в звичайних “лінійних” термінах, ми повинні використовувати багато 0 для представлення значень у прикладах 1 і 2. Чесно кажучи, якби ми побудували графік чогось подібного до сигналу 1 у часі, ми б навіть не побачили рівень шуму. Наприклад, якби шкала осі Y змінювалася від 0 до 3 Вт, шум був би надто малим, щоб його можна було побачити на графіку. Щоб представити ці шкали одночасно, ми працюємо в логарифмічній шкалі.

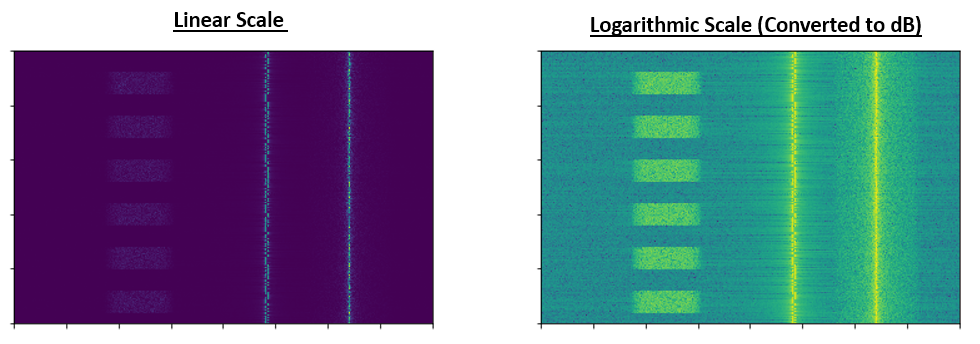
Щоб ще більше проілюструвати проблеми масштабу, з якими ми стикаємося при обробці сигналів, розглянемо наведені нижче водоспади трьох однакових сигналів. Ліворуч - вихідний сигнал у лінійному масштабі, а праворуч - сигнали, перетворені в логарифмічну шкалу (дБ). Обидва представлення використовують однакову кольорову карту, де синій колір означає найнижче значення, а жовтий - найвище. Ви ледве можете побачити сигнал зліва в лінійній шкалі.

Зображення того, чому важливо розуміти дБ або децибели, показуючи спектрограму з використанням лінійної та логарифмічної шкали

Для заданого значення x ми можемо представити x у дБ за допомогою наступної формули:

$x_{dB} = 10 \log_{10} x$

У мові Python

x_db = 10.0 * np.log10(x)

Ви могли бачити, що 10 * може бути 20 * в інших доменах. Щоразу, коли ви маєте справу з якоюсь потужністю, ви використовуєте 10, і ви використовуєте 20, якщо ви маєте справу з неенергетичними величинами, такими як напруга або струм. В DSP ми, як правило, маємо справу з потужністю. Насправді, в цьому підручнику немає жодного разу, коли нам потрібно було б використовувати 20 замість 10.

Ми перетворюємо з дБ назад в лінійні (звичайні числа) за допомогою:

$x = 10^{x_{dB}/10}$

У Python

x = 10.0 ** (x_db / 10.0)

Не зациклюйтеся на формулі, оскільки тут є ключова концепція, яку потрібно винести за дужки. В DSP ми маємо справу з дуже великими і дуже малими числами (наприклад, рівень сигналу в порівнянні з рівнем шуму). Логарифмічна шкала в дБ дозволяє нам мати більший динамічний діапазон, коли ми виражаємо числа або будуємо графіки. Вона також надає деякі зручності, наприклад, можливість додавання, коли ми зазвичай множимо (як ми побачимо у розділі Розрахунок бюджету лінії зв’язку).

Деякі типові помилки, з якими можуть зіткнутися новачки у dB, такі:

Використання натурального лога замість лога з основою 10, оскільки функція log() у більшості мов програмування насправді є натуральним логом.
Забути включити дБ при вираженні числа або позначенні осі. Якщо ми маємо справу з дБ, нам потрібно десь його позначити.
Коли ви використовуєте дБ, ви додаєте/віднімаєте значення замість того, щоб множити/ділити, наприклад:

Також важливо розуміти, що дБ технічно не є “одиницею”. Значення в дБ саме по собі не має одиниць виміру, наприклад, якщо щось в 2 рази більше, то одиниць виміру немає, поки я не скажу вам одиниці виміру. дБ - це відносна величина. В аудіо, коли говорять дБ, насправді мають на увазі дБА, що є одиницею вимірювання рівня звуку (A - це одиниці). У бездротовому зв’язку ми зазвичай використовуємо вати для позначення фактичного рівня потужності. Тому ви можете побачити dBW як одиницю, яка відноситься до 1 Вт. Ви також можете побачити dBmW (часто пишуть dBm для скорочення), яка відноситься до 1 мВт. Наприклад, хтось може сказати “наш передавач налаштований на 3 дБВт” (тобто 2 Вт). Іноді ми використовуємо дБ сам по собі, маючи на увазі, що він відносний і не має одиниць виміру. Можна сказати: “наш сигнал був прийнятий на 20 дБ вище рівня шуму”. Ось невелика підказка: 0 дБм = -30 дБВт.

Ось кілька поширених перетворень, які я рекомендую запам’ятати:

Лінійні	дБ
1x	0 дБ
2x	3 дБ
10x	10 дБ
0.5x	-3 дБ
0.1x	-10 дБ
100x	20 дБ
1000x	30 дБ
10000x	40 дБ

Нарешті, щоб розглянути ці цифри в перспективі, нижче наведені деякі приклади рівнів потужності в дБм:

80 дБм	Передавальна потужність сільської FM-радіостанції
62 дБм	Максимальна потужність радіоаматорського передавача
60 дБм	Потужність типової домашньої мікрохвильової печі
37 дБм	Максимальна потужність типової портативної радіостанції CB або радіоаматорської радіостанції
27 дБм	Типова потужність передавача мобільного телефону
15 дБм	Типова потужність передачі WiFi
10 дБм	Максимальна потужність передачі Bluetooth (версія 4)
-10 дБм	Максимальна потужність прийому для WiFi
-70 дБм	Приклад прийнятої потужності для радіосигналу
-100 дБм	Мінімальна потужність прийому для WiFi
-127 дБм	Типова потужність прийому від супутників GPS

Шум в частотній області¶

У розділі Частотний домен ми розглянули “пари Фур’є”, тобто те, як певний сигнал часової області виглядає у частотній області. Як же виглядає гаусівський шум у частотній області? На наступних графіках показано деякий змодельований шум у часовій області (вгорі) і графік спектральної щільності потужності (PSD) цього шуму (внизу). Ці графіки взято з GNU Radio.

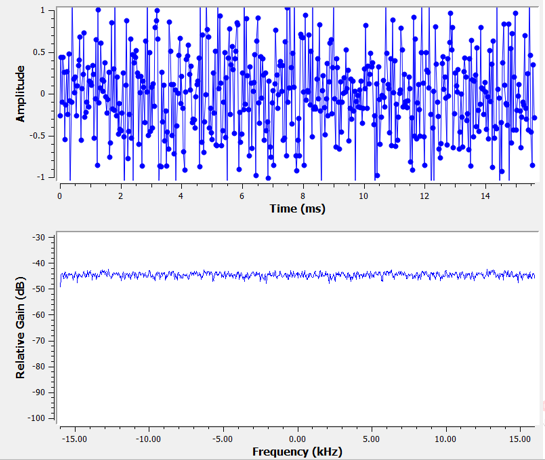
AWGN у часовій області - це також гаусівський шум у частотній області, хоча він виглядає як плоска лінія, якщо взяти амплітуду і виконати усереднення

Ми бачимо, що він виглядає приблизно однаково на всіх частотах і є досить плоским. Виходить, що гаусівський шум у часовій області є також гаусівським шумом у частотній області. Так чому ж два графіки вище не виглядають однаково? Це тому, що графік в частотній області показує величину ШПФ, тому там будуть тільки позитивні числа. Важливо, що він використовує логарифмічну шкалу, або показує величину в дБ. Інакше ці графіки виглядали б однаково. Ми можемо довести це собі, згенерувавши деякий шум (у часовій області) у Python, а потім отримавши ШПФ.

import numpy as np
import matplotlib.pyplot as plt

N = 1024 # кількість відліків для моделювання, виберіть будь-яке число
x = np.random.randn(N)
plt.plot(x, '.-')
plt.show()

X = np.fft.fftshift(np.fft.fft(x))
X = X[N/2:] # дивимось тільки додатні частоти. пам'ятайте, що // це просто цілочисельне ділення
plt.plot(np.real(X), '.-')
plt.show()

Зверніть увагу, що функція randn() за замовчуванням використовує mean = 0 і variance = 1. Обидва графіки будуть виглядати приблизно так:

Потім ви можете створити пласку PSD, яку ми мали у GNU Radio, взявши запис і усереднивши його разом. Сигнал, який ми згенерували і взяли ШПФ, був реальним сигналом (а не комплексним), і ШПФ будь-якого реального сигналу матиме відповідні від’ємні та додатні частини, тому ми зберегли лише додатну частину результату ШПФ (2-гу половину). Але чому ми згенерували лише “реальний” шум, і як комплексні сигнали пов’язані з цим?

Комплексний шум¶

“Комплексний гаусівський” шум - це те, що ми відчуваємо, коли маємо сигнал в основній смузі частот; потужність шуму ділиться між реальною та уявною частинами порівну. І найголовніше, що реальна та уявна частини не залежать одна від одної; знаючи значення однієї з них, ви не отримаєте значення іншої.

Ми можемо згенерувати складний гаусівський шум у Python за допомогою

n = np.random.randn() + 1j * np.random.randn()

Але зачекайте! Наведене вище рівняння не генерує таку ж “кількість” шуму, як np.random.randn(), з точки зору потужності (відомої як потужність шуму). Ми можемо знайти середню потужність сигналу (або шуму) з нульовим середнім значенням за допомогою:

power = np.var(x)

де np.var() - функція для дисперсії. Тут потужність нашого сигналу n дорівнює 2. Для того, щоб згенерувати складний шум з “одиничною потужністю”, тобто потужністю 1 (що робить речі зручними), ми повинні використовувати

n = (np.random.randn(N) + 1j*np.random.randn(N))/np.sqrt(2) # AWGN з одиничною потужністю

Для побудови графіка складного шуму в часовій області, як і будь-якого складного сигналу, нам знадобляться два рядки:

n = (np.random.randn(N) + 1j*np.random.randn(N))/np.sqrt(2)
plt.plot(np.real(n),'.-')
plt.plot(np.imag(n),'.-')
plt.legend(['real','imag'])
plt.show()

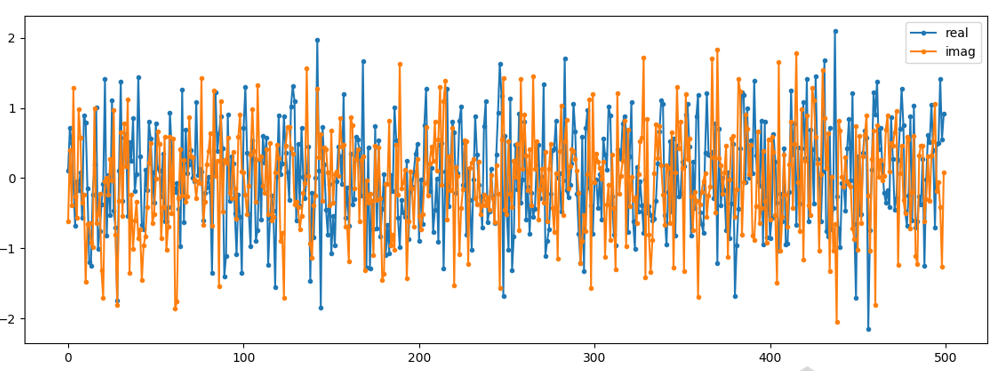
Ви можете бачити, що дійсна та уявна частини повністю незалежні.

Як виглядає складний гаусівський шум на IQ-діаграмі? Пам’ятайте, що графік IQ показує дійсну частину (горизонтальна вісь) і уявну частину (вертикальна вісь), обидві з яких є незалежними випадковими гаусівськими величинами.

plt.plot(np.real(n),np.imag(n),'.')
plt.grid(True, which='both')
plt.axis([-2, 2, -2, 2])
plt.show()

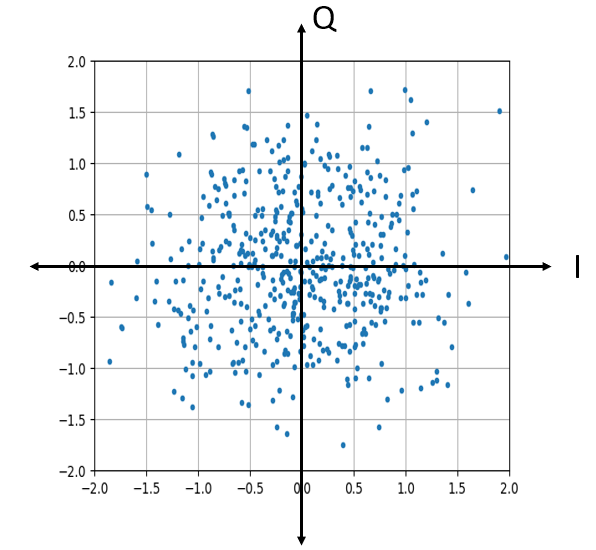
Складний шум на графіку IQ або сузір'їв, змодельований у Python

Це виглядає так, як ми і очікували: випадкова пляма з центром в 0 + 0j, або в початку координат. Заради інтересу спробуємо додати шум до QPSK-сигналу, щоб побачити, як виглядає IQ-діаграма:

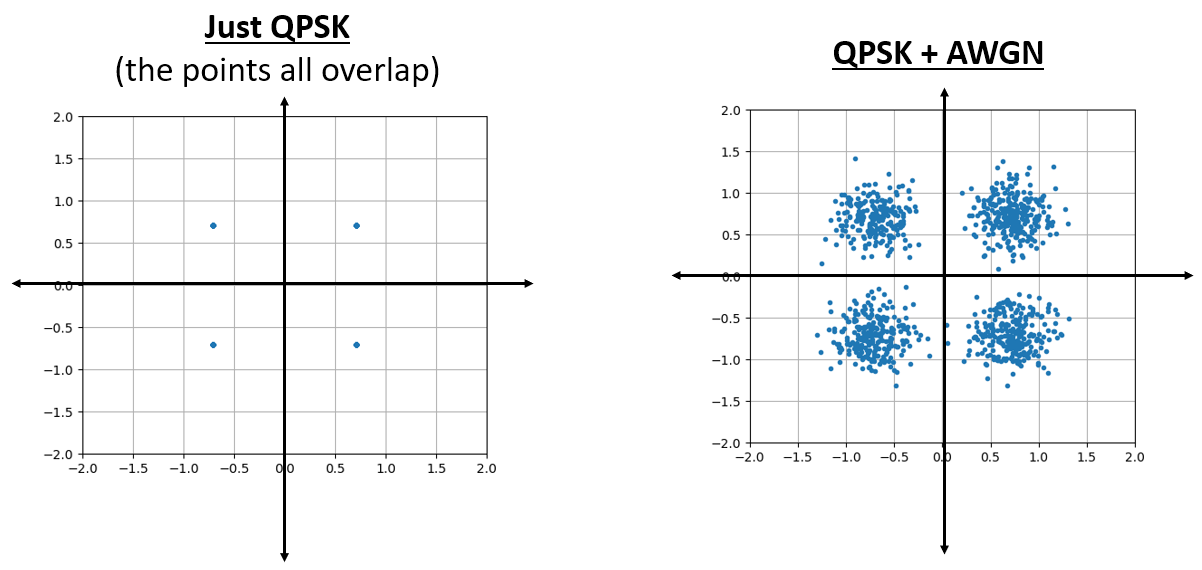
А що станеться, коли шум буде сильнішим?

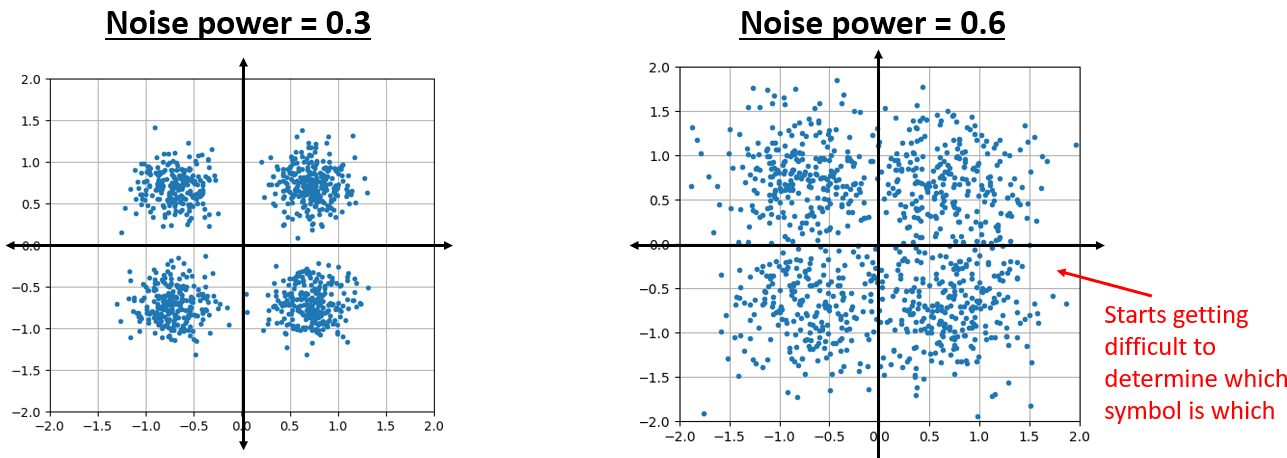
Ми починаємо розуміти, чому передача даних бездротовим способом не така проста. Ми хочемо відправити якомога більше бітів на символ, але якщо шум занадто високий, ми отримаємо помилкові біти на приймальному боці.

AWGN¶

Additive White Gaussian Noise (AWGN) - це абревіатура, яку ви часто чуєте в світі DSP і SDR. Про GN, гауссівський шум, ми вже говорили. Адитивний просто означає, що шум додається до прийнятого сигналу. Білий колір в частотній області означає, що спектр є плоским у всій смузі спостереження. На практиці він майже завжди буде білим, або приблизно білим. У цьому підручнику ми будемо використовувати AWGN як єдину форму шуму, коли маємо справу з лініями зв’язку, бюджетами ліній зв’язку тощо. Шум, який не є AWGN, як правило, є вузькоспеціалізованою темою.

SNR і SINR¶

Відношення сигнал/шум (SNR) - це те, як ми будемо вимірювати різницю в силі між сигналом і шумом. Це відношення не має одиниць виміру. На практиці SNR майже завжди вимірюється в дБ. Часто при моделюванні ми кодуємо сигнали таким чином, щоб вони мали одиничну потужність (потужність = 1). Таким чином, ми можемо створити SNR 10 дБ, генеруючи шум потужністю -10 дБ, регулюючи дисперсію під час генерації шуму.

$\mathrm{SNR} = \frac{P_{signal}}{P_{noise}}$

$\mathrm{SNR_{dB}} = P_{signal\_dB} - P_{noise\_dB}$

Якщо хтось каже “SNR = 0 дБ”, це означає, що потужність сигналу і шуму однакова. Позитивне значення SNR означає, що наш сигнал має більшу потужність, ніж шум, тоді як негативне значення SNR означає, що шум має більшу потужність. Виявлення сигналів з від’ємним SNR зазвичай досить складне.

Як ми вже згадували раніше, потужність сигналу дорівнює дисперсії сигналу. Отже, ми можемо представити SNR як відношення дисперсії сигналу до дисперсії шуму:

$\mathrm{SNR} = \frac{P_{signal}}{P_{noise}} = \frac{\sigma^2_{signal}}{\sigma^2_{noise}}$

Відношення сигнал/завада плюс шум (SINR) по суті те саме, що й SNR, за винятком того, що до знаменника ви додаєте заваду разом із шумом.

$\mathrm{SINR} = \frac{P_{signal}}{P_{interference} + P_{noise}}$

Що є завадою, залежить від застосування/ситуації, але зазвичай це інший сигнал, який заважає сигналу, що становить інтерес (SOI), і який або перекриває SOI по частоті, або не може бути відфільтрований з якихось причин.

PySDR: Посібник з SDR та DSP за допомогою Python