3. Вибірка IQ¶

У цій главі ми представляємо концепцію під назвою IQ вибірка, також відома як комплексна вибірка або квадратурна вибірка. Ми також розглядаємо дискретизацію Найквіста, комплексні числа, радіочастотні носії, понижувальне перетворення та спектральну щільність потужності. Вибірка IQ — це форма вибірки, яку виконує SDR, а також багато цифрових приймачів (і передавачів). Це дещо складніша версія звичайної цифрової вибірки (каламбур), тому ми будемо робити це повільно, і з деякою практикою ця концепція обов’язково спрацює!

Основи вибірки¶

Перш ніж перейти до вибірки IQ, давайте обговоримо, що насправді означає вибірка. Можливо, ви стикалися із семплюванням, не усвідомлюючи цього, записуючи звук за допомогою мікрофона. Мікрофон — це перетворювач, який перетворює звукові хвилі в електричний сигнал (рівень напруги). Цей електричний сигнал перетворюється аналого-цифровим перетворювачем (АЦП), створюючи цифрове представлення звукової хвилі. Щоб спростити, мікрофон вловлює звукові хвилі, які перетворюються на електрику, а ця електрика, у свою чергу, перетворюється на числа. АЦП діє як міст між аналоговою та цифровою областями. СПЗ напрочуд схожі. Однак замість мікрофона вони використовують антену, хоча вони також використовують АЦП. В обох випадках рівень напруги вимірюється за допомогою АЦП. Для СПЗ подумайте, що радіохвилі входять, а потім зменшуються.

Незалежно від того, чи ми маємо справу з аудіо чи радіочастотами, ми повинні взяти вибірку, якщо ми хочемо захопити, обробити або зберегти сигнал у цифровому вигляді. Вибірка може здатися простою, але в ній багато чого. Більш технічний спосіб дискретизації сигналу полягає в тому, щоб отримати значення в певний момент часу та зберегти їх у цифровому вигляді. Скажімо, у нас є якась випадкова функція $S(t)$ , яка може представляти будь-що, і це неперервна функція, яку ми хочемо взяти на вибірку:

Concept of sampling a signal, showing sample period T, the samples are the blue dots

Ми записуємо значення $S(t)$ через рівні проміжки в $T$ секунди, відомі як період вибірки. Частота, з якою ми беремо вибірку, тобто кількість вибірок, взятих за секунду, є просто $\frac{1}{T}$ . Ми називаємо це частотою дискретизації, і вона зворотна до періоду дискретизації. Наприклад, якщо ми маємо частоту дискретизації 10 Гц, то період дискретизації становить 0,1 секунди; між кожним зразком буде 0,1 секунди. На практиці наші частоти дискретизації будуть порядку сотень кГц до десятків МГц або навіть вище. Коли ми знімаємо сигнали, ми повинні пам’ятати про частоту дискретизації, це дуже важливий параметр.

Для тих, хто вважає за краще бачити математику; нехай $S_n$ представляє вибірку $n$ , зазвичай ціле число, починаючи з 0. Використовуючи цю угоду, процес вибірки може бути представлений математично як $S_n = S(nT)$ для цілих значень $n$ . Тобто ми оцінюємо аналоговий сигнал $S(t)$ на цих інтервалах $nT$ .

Вибірка Найквіста¶

Для даного сигналу головним питанням часто є те, як швидко ми повинні проводити вибірку? Давайте розглянемо сигнал, який є просто синусоїдальною хвилею частоти f, показаної зеленим кольором нижче. Скажімо, ми беремо вибірку зі швидкістю Fs (зразки показано синім кольором). Якщо ми відберемо цей сигнал зі швидкістю, що дорівнює f (тобто Fs = f), ми отримаємо щось таке:

:: ../_images/sampling_Fs_0.3.svg

align:	center

Червона пунктирна лінія на наведеному вище зображенні реконструює іншу (неправильну) функцію, яка могла призвести до запису тих самих семплів. Вона вказує на те, що наша частота дискретизації була занадто низькою, тому що ті самі відліки могли бути отримані від двох різних функцій, що призвело до неоднозначності. Якщо ми хочемо точно реконструювати оригінальний сигнал, ми не можемо допустити такої неоднозначності.

Спробуймо дискретизувати трохи швидше, з Fs = 1.2f:

Знову ж таки, існує інший сигнал, який може відповідати цим вибіркам. Ця неоднозначність означає, що якби хтось надав нам цей список зразків, ми не змогли б розрізнити, який сигнал є оригінальним, на основі нашої вибірки.

А як щодо дискретизації при Fs = 1.5f:

Приклад неоднозначності дискретизації, коли сигнал відбирається недостатньо швидко (нижче швидкості Найквіста)

Все ще недостатньо швидко! Згідно з теорією DSP, в яку ми не будемо занурюватися, вам потрібно робити вибірки з частотою, вдвічі більшою за частоту сигналу, щоб усунути неоднозначність, з якою ми стикаємося:

Цього разу немає неправильного сигналу, тому що ми робили вибірки досить швидко, щоб не існувало жодного сигналу, який би відповідав цим вибіркам, окрім того, який ви бачите (якщо тільки ви не підніметеся вище за частотою, але про це ми поговоримо пізніше).

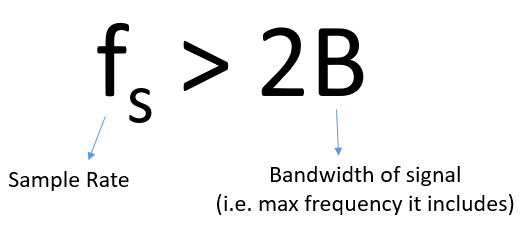
У наведеному вище прикладі наш сигнал був простою синусоїдою, більшість реальних сигналів матимуть багато частотних складових. Для точної дискретизації будь-якого сигналу частота дискретизації повинна бути “щонайменше вдвічі більшою за частоту максимальної частотної складової”. Ось візуалізація на прикладі графіку частотної області, зверніть увагу, що завжди буде існувати рівень шуму, тому найвища частота зазвичай є наближеним значенням:

Дискретизація Найквіста означає, що частота дискретизації вища за максимальну смугу пропускання сигналу

Ми повинні визначити найвищу частотну складову, потім подвоїти її, і переконатися, що ми робимо вибірку з такою частотою або швидше. Мінімальна частота, з якою ми можемо робити вибірку, називається частотою Найквіста. Іншими словами, частота Найквіста - це мінімальна частота, з якою сигнал (зі скінченною смугою пропускання) повинен бути дискретизований, щоб зберегти всю його інформацію. Це надзвичайно важлива частина теорії в DSP і SDR, яка служить мостом між безперервними і дискретними сигналами.

Якщо ми робимо вибірку недостатньо швидко, ми отримуємо те, що називається аліасинг, про який ми дізнаємось пізніше, але ми намагаємось уникати цього за будь-яку ціну. Наші SDR (і більшість приймачів взагалі) відфільтровують все, що перевищує Fs/2, безпосередньо перед тим, як виконується дискретизація. Якщо ми спробуємо прийняти сигнал із занадто низькою частотою дискретизації, цей фільтр відсіче частину сигналу. Наші SDR роблять все можливе, щоб забезпечити нас зразками, вільними від аліасингу та інших недосконалостей.

Квадратурна дискретизація¶

Термін “квадратура” має багато значень, але в контексті DSP і SDR він відноситься до двох хвиль, які знаходяться на 90 градусів у протифазі. Чому 90 градусів у протифазі? Подумайте про те, що дві хвилі, які знаходяться в протифазі на 180 градусів, по суті, є однією і тією ж хвилею, але помноженою на -1. При зсуві на 90 градусів вони стають ортогональними, а з ортогональними функціями можна робити багато цікавих речей. Для простоти ми використаємо синус і косинус як дві синусоїди, що зсунуті на 90 градусів у фазі.

Далі призначимо змінні для представлення амплітуди синуса і косинуса. Ми будемо використовувати $I$ для cos() і $Q$ для sin():

$I \cos(2\pi ft) Q \sin(2\pi ft)$

Ми можемо побачити це візуально, побудувавши графік I і Q, що дорівнює 1:

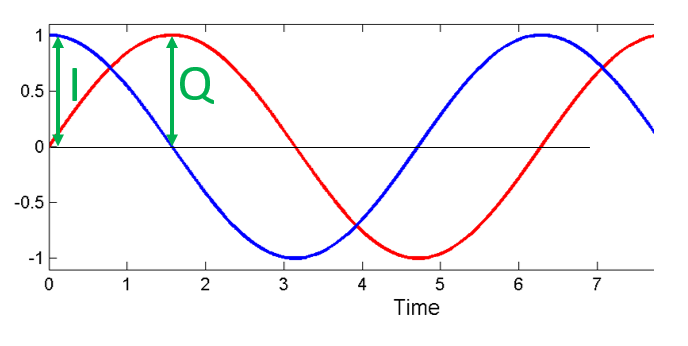
I і Q візуалізуються як амплітуди синусоїд, які підсумовуються разом

Ми називаємо cos() “синфазним” компонентом, звідси і назва I, а sin() - зсув на 90 градусів або “квадратурний” компонент, звідси і назва Q. Хоча якщо ви випадково переплутаєте їх і віднесете Q до cos(), а I до sin(), це не матиме значення для більшості ситуацій.

Дискретизацію IQ легше зрозуміти, використовуючи точку зору передавача, тобто розглядаючи задачу передачі радіосигналу через повітря. Ми хочемо передати одну синусоїду з певною фазою, що можна зробити, передавши суму sin() і cos() з фазою 0, завдяки тригонометричній тотожності: $a \cos(x) + b \sin(x) = A \cos(x-\phi)$ . Нехай x(t) - це наш сигнал для передачі:

$x(t) = I \cos(2\pi ft) + Q \sin(2\pi ft)$

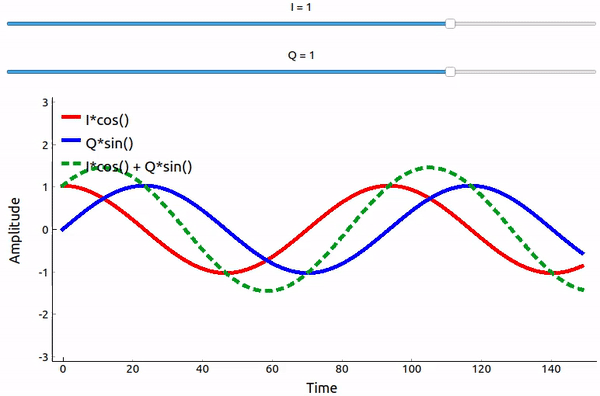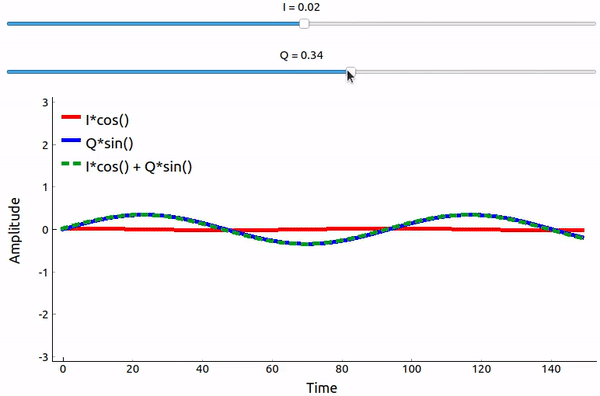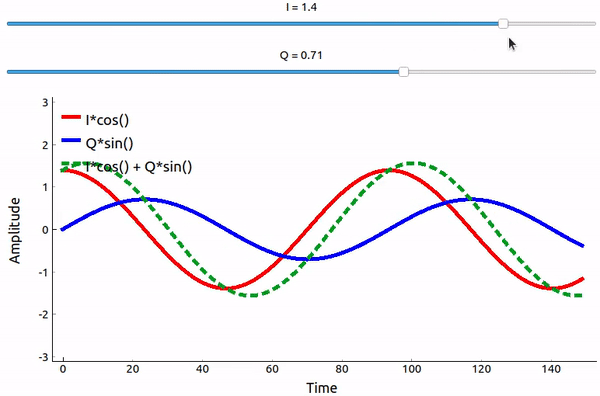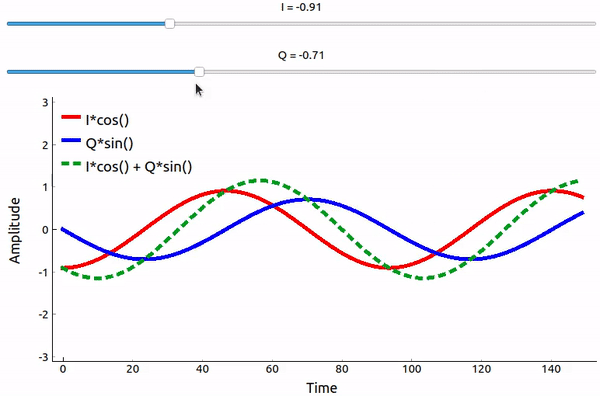
Що відбувається, коли ми додаємо синус і косинус? Або, точніше, що станеться, коли ми додамо дві синусоїди, які зсунуті на 90 градусів у фазі? У відео нижче є повзунок для регулювання I і повзунок для регулювання Q. На графіку зображені косинус, синус, а потім їхня сума.

Анімація GNU Radio, що показує I та Q як амплітуди синусоїд, які підсумовуються разом

(Код, використаний для цієї програми на основі pyqtgraph у Python, можна знайти тут)

Важливим висновком є те, що коли ми додаємо cos() і sin(), ми отримуємо ще одну чисту синусоїду з іншою фазою і амплітудою. Крім того, фаза зміщується, коли ми повільно видаляємо або додаємо одну з двох частин. Амплітуда також змінюється. Це все є результатом тригонометричної тотожності: $a \cos(x) + b \sin(x) = A \cos(x-\phi)$ , до якої ми повернемося трохи згодом. “Корисність” такої поведінки полягає в тому, що ми можемо керувати фазою і амплітудою результуючої синусоїди, змінюючи амплітуди I і Q (нам не потрібно змінювати фазу косинуса або синуса). Наприклад, ми можемо регулювати I і Q таким чином, щоб амплітуда залишалася постійною, а фаза була такою, якою ми хочемо. Для передавача ця здатність надзвичайно корисна, оскільки ми знаємо, що нам потрібно передавати синусоїдальний сигнал, щоб він пролетів у повітрі у вигляді електромагнітної хвилі. І набагато простіше відрегулювати дві амплітуди і виконати операцію додавання, ніж відрегулювати амплітуду і фазу. В результаті наш передавач буде виглядати приблизно так:

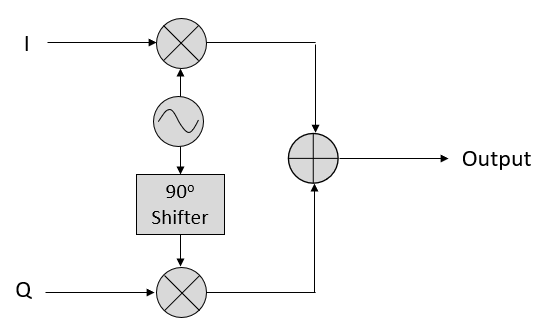
Діаграма, що показує, як I і Q модулюються на несучу

Нам потрібно згенерувати лише одну синусоїду і зсунути її на 90 градусів, щоб отримати Q-частину.

Комплексні числа¶

Зрештою, IQ - це альтернативний спосіб представлення амплітуди і фази, який приводить нас до комплексних чисел і можливості представляти їх на комплексній площині. Можливо, ви вже зустрічалися з комплексними числами в інших класах. Візьмемо для прикладу комплексне число 0.7-0.4j:

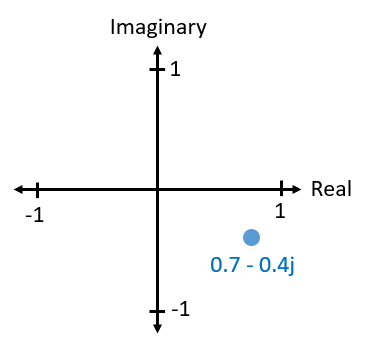
Комплексне число - це просто два числа разом, дійсна і уявна частина. Комплексне число також має амплітуду і фазу, що має більше сенсу, якщо думати про нього як про вектор, а не точку. Величина - це довжина лінії між початком координат і точкою (тобто довжина вектора), а фаза - це кут між вектором і 0 градусів, який ми визначаємо як додатну дійсну вісь:

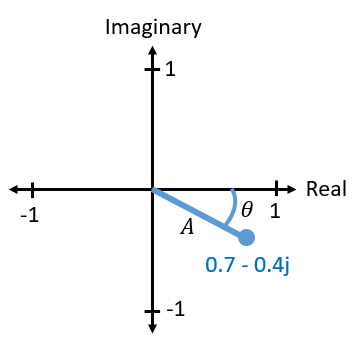
Таке представлення синусоїди відоме як “фазорна діаграма”. Це просто побудова комплексних чисел і поводження з ними як з векторами. Яка ж величина і фаза нашого прикладу комплексного числа 0.7-0.4j? Для даного комплексного числа, де $a$ - дійсна частина, а $b$ - уявна частина:

$\mathrm{magnitude} = \sqrt{a^2 + b^2} = 0.806 \mathrm{phase} = \tan^{-1} \left( \frac{b}{a} \right) = -29.7^{\circ} = -0.519 \quad \mathrm{radians}$

У Python ви можете використовувати функції np.abs(x) і np.angle(x) для амплітуди і фази. На вхід може подаватися комплексне число або масив комплексних чисел, а на виході буде дійсне число (з типом даних float).

Можливо, ви вже з’ясували, як ця векторна або фазова діаграма пов’язана з умовною позначкою IQ: I - це дійсне число, а Q - уявне. З цього моменту, коли ми будемо малювати комплексну площину, ми будемо позначати її не дійсними і уявними числами, а I і Q. Це все одно комплексні числа!

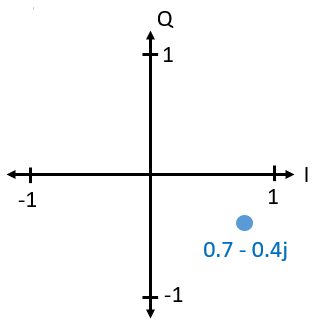
Тепер припустимо, що ми хочемо передати наш приклад точки 0.7-0.4j. Ми будемо передавати:

$x(t) = I \cos(2\pi ft) + Q \sin(2\pi ft) \quad \quad \quad = 0.7 \cos(2\pi ft) - 0.4 \sin(2\pi ft)$

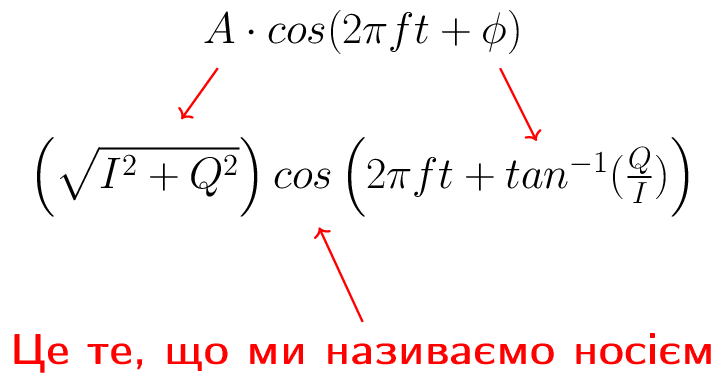
Ми можемо використати тригонометричну тотожність $a \cos(x) + b \sin(x) = A \cos(x-\phi)$ , де $A$ - наша величина, знайдена за допомогою $\sqrt{I^2 + Q^2}$ і $\phi$ - наша фаза, яка дорівнює $\tan^{-1} \left( Q/I \right)$ . Вищенаведене рівняння набуває вигляду:

$x(t) = 0.806 \cos(2\pi ft + 0.519)$

Незважаючи на те, що ми почали з комплексного числа, те, що ми передаємо, є реальним сигналом з певною амплітудою і фазою; насправді ви не можете передати щось уявне за допомогою електромагнітних хвиль. Ми просто використовуємо уявні/комплексні числа для представлення того, “що” ми передаємо. Незабаром ми поговоримо про $f$ .

Комплексні числа у ШПФ¶

Наведені вище комплексні числа розглядалися як приклади часової області, але ви також зіткнетеся з комплексними числами, коли будете застосовувати ШПФ. Коли ми розглядали ряди Фур’є і ШПФ в минулому розділі, ми ще не занурювалися в комплексні числа. Коли ви застосовуєте ШПФ до серії відліків, він знаходить представлення в частотній області. Ми говорили про те, як ШПФ з’ясовує, які частоти існують в цьому наборі відліків (величина ШПФ вказує на силу кожної частоти). Але ШПФ також обчислює затримку (часовий зсув), необхідну для застосування до кожної з цих частот, щоб набір синусоїд можна було скласти для відновлення сигналу в часовій області. Ця затримка є просто фазою ШПФ. Результатом ШПФ є масив комплексних чисел, і кожне комплексне число дає вам амплітуду і фазу, а індекс цього числа дає вам частоту. Якщо ви згенеруєте синусоїди на цих частотах/амплітудах/фазах і підсумуєте їх разом, ви отримаєте вихідний сигнал в часовій області (або щось дуже близьке до нього, і саме тут вступає в дію теорема дискретизації Найквіста).

Сторона приймача¶

Тепер давайте подивимось на радіоприймач, який намагається прийняти сигнал (наприклад, FM-радіосигнал). Використовуючи IQ-семплінг, діаграма тепер має такий вигляд:

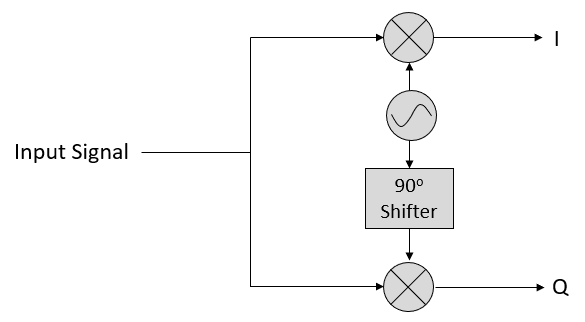
Отримання зразків IQ шляхом прямого множення вхідного сигналу на синусоїду і зсунуту на 90 градусів версію цієї синусоїди

На вхід надходить реальний сигнал, отриманий на нашу антену, і він перетворюється на значення IQ. Ми робимо вибірку гілок I і Q окремо, використовуючи два АЦП, а потім об’єднуємо пари і зберігаємо їх у вигляді комплексних чисел. Іншими словами, на кожному кроці ви будете відбирати одне значення I і одне значення Q і об’єднувати їх у вигляді $I + jQ$ (тобто, одне комплексне число на вибірку IQ). Завжди буде існувати “частота дискретизації”, тобто швидкість, з якою виконується вибірка. Хтось може сказати: “У мене є SDR з частотою дискретизації 2 МГц”. Вони мають на увазі, що SDR отримує два мільйони відліків IQ в секунду.

Якщо хтось дасть вам купу відліків IQ, це буде виглядати як одномірний масив/вектор комплексних чисел. Саме до цього моменту, комплексного чи ні, ми будували всю цю главу, і ми нарешті досягли його.

Протягом усього підручника ви будете дуже добре знайомі з тим, як працюють IQ-тести, як їх отримувати та передавати за допомогою SDR, як обробляти їх у Python і як зберігати у файл для подальшого аналізу.

Останнє важливе зауваження: на рисунку вище показано, що відбувається всередині SDR. Насправді нам не потрібно генерувати синусоїду, зсувати на 90, множити або додавати - SDR робить це за нас. Ми повідомляємо SDR, на якій частоті ми хочемо зробити вибірку, або на якій частоті ми хочемо передати наші вибірки. На стороні приймача SDR надасть нам зразки IQ. На стороні передавача ми повинні надати SDR зразки IQ. З точки зору типу даних, це будуть або складні числа, або числа з плаваючою точкою.

Перетворення носія і понижуючий коефіцієнт¶

До цього моменту ми не обговорювали частоту, але ми бачили, що в рівняннях, що включають cos() і sin() є $f$ . Ця частота є центральною частотою сигналу, який ми фактично посилаємо через повітря (частота електромагнітної хвилі). Ми називаємо її “несучою”, тому що вона переносить наш сигнал на певній радіочастоті. Коли ми налаштовуємося на частоту за допомогою SDR і отримуємо відліки, наша інформація зберігається в I і Q; ця несуча не відображається в I і Q, якщо припустити, що ми налаштувалися на несучу.

Figure made with TikZ

Для довідки: радіосигнали, такі як FM-радіо, WiFi, Bluetooth, LTE, GPS тощо, зазвичай використовують частоту (тобто несучу) між 100 МГц і 6 ГГц. Ці частоти дуже добре поширюються в повітрі, але вони не потребують наддовгих антен або великої потужності для передачі чи прийому. Ваша мікрохвильова піч готує їжу за допомогою електромагнітних хвиль на частоті 2,4 ГГц. Якщо дверцята мікрохвильової печі протікають, вона глушитиме сигнали WiFi і, можливо, також обпече вашу шкіру. Іншою формою електромагнітних хвиль є світло. Видиме світло має частоту близько 500 ТГц. Це настільки висока частота, що ми не використовуємо традиційні антени для передачі світла. Ми використовуємо такі методи, як світлодіоди, які є напівпровідниковими пристроями. Вони створюють світло, коли електрони перескакують між атомними орбітами напівпровідникового матеріалу, і колір залежить від того, як далеко вони перескакують. Технічно радіочастота (РЧ) визначається як діапазон від приблизно 20 кГц до 300 ГГц. Це частоти, на яких енергія електричного струму, що коливається, може випромінюватися з провідника (антени) і поширюватися в просторі. Діапазон від 100 МГц до 6 ГГц є найбільш корисними частотами, принаймні для більшості сучасних застосувань. Частоти вище 6 ГГц десятиліттями використовувалися для радарів і супутникового зв’язку, а зараз застосовуються в 5G “mmWave” (24 - 29 ГГц) для доповнення нижніх діапазонів і збільшення швидкості.

Коли ми швидко змінюємо значення IQ і передаємо нашу несучу, це називається “модуляцією” несучої (даними або чим завгодно). Коли ми змінюємо I і Q, ми змінюємо фазу і амплітуду несучої. Інший варіант - змінити частоту несучої, тобто зсунути її трохи вгору або вниз, як це робить FM-радіо.

Як простий приклад, скажімо, ми передаємо зразок IQ 1+0j, а потім переходимо на передачу 0+1j. Ми переходимо від передачі $\cos(2\pi ft)$ до $\sin(2\pi ft)$ , тобто наша несуча зсувається по фазі на 90 градусів, коли ми переходимо від однієї вибірки до іншої.

Легко заплутатися між сигналом, який ми хочемо передати (який зазвичай містить багато частотних компонентів), і частотою, на якій ми його передаємо (наша несуча частота). Сподіваємось, це стане зрозумілим, коли ми розглянемо базові та смугові сигнали.

А тепер повернемося на секунду до дискретизації. Замість того, щоб отримувати відліки шляхом множення сигналу з антени на cos() і sin(), а потім записувати I і Q, що, якби ми подавали сигнал з антени на один АЦП, як в архітектурі з прямою дискретизацією, яку ми щойно обговорювали? Скажімо, несуча частота 2,4 ГГц, як у WiFi або Bluetooth. Це означає, що нам доведеться робити вибірки на частоті 4,8 ГГц, як ми вже дізналися. Це надзвичайно швидко! АЦП, який робить такі швидкі вибірки, коштує тисячі доларів. Замість цього ми “понижуємо” сигнал так, щоб сигнал, який ми хочемо отримати, був зосереджений навколо постійного струму або 0 Гц. Це перетворення відбувається до того, як ми зробимо вибірку. Ми переходимо від

$I \cos(2\pi ft) Q \sin(2\pi ft)$

до просто I та Q.

Візуалізуємо даунконверсію у частотній області:

Процес понижувального перетворення, коли сигнал зміщується по частоті від ВЧ до 0 Гц або базової смуги

Коли ми відцентрували сигнал на 0 Гц, максимальна частота вже не становить 2,4 ГГц, а базується на характеристиках сигналу, оскільки ми видалили несучу. Більшість сигналів мають ширину смуги пропускання від 100 кГц до 40 МГц, тому за допомогою низхідного перетворення ми можемо робити вибірки на набагато нижчій частоті. І B2X0 USRP, і PlutoSDR містять радіочастотну інтегральну схему (RFIC), яка може робити вибірки на частоті до 56 МГц, що досить високо для більшості сигналів, з якими ми зустрінемося.

Нагадуємо, що процес пониження частоти виконується нашим SDR; як користувачеві SDR нам не потрібно нічого робити, окрім як вказати йому, на яку частоту налаштовуватися. Низькочастотне (і високочастотне) перетворення здійснюється за допомогою компонента, який називається мікшером, що зазвичай зображується на схемах у вигляді символу множення всередині кола. Мікшер приймає сигнал, виводить перетворений вниз/вгору сигнал і має третій порт, який використовується для підключення генератора. Частота генератора визначає зсув частоти, що застосовується до сигналу, а мікшер, по суті, є просто функцією множення (нагадаємо, що множення на синусоїду викликає зсув частоти).

Нарешті, вам може бути цікаво, як швидко сигнали поширюються в повітрі. Згадайте з шкільного курсу фізики, що радіохвилі - це просто електромагнітні хвилі на низьких частотах (приблизно від 3 кГц до 80 ГГц). Видиме світло - це також електромагнітні хвилі, але на значно вищих частотах (від 400 ТГц до 700 ТГц). Всі електромагнітні хвилі поширюються зі швидкістю світла, яка становить близько 3e8 м/с, принаймні, коли вони проходять через повітря або вакуум. Оскільки вони завжди рухаються з однаковою швидкістю, відстань, яку хвиля проходить за одне повне коливання (один повний цикл синусоїди), залежить від її частоти. Ми називаємо цю відстань довжиною хвилі і позначаємо її $\lambda$ . Ви, мабуть, бачили цю залежність раніше:

$f = \frac{c}{\lambda}$

де $c$ - швидкість світла, зазвичай дорівнює 3e8, коли $f$ - у Гц, а $\lambda$ - у метрах. У бездротовому зв’язку це співвідношення стає важливим, коли ми переходимо до антен, тому що для прийому сигналу на певній несучій частоті, $f$ , потрібна антена, яка відповідає його довжині хвилі, $\lambda$ , зазвичай антена має $\lambda/2$ або $\lambda/4$ довжину. Однак, незалежно від частоти/довжини хвилі, інформація, що міститься в цьому сигналі, завжди буде рухатися зі швидкістю світла від передавача до приймача. При обчисленні цієї затримки в повітрі можна скористатися емпіричним правилом, що світло проходить приблизно один фут за одну наносекунду. Ще одне емпіричне правило: сигнал, що проходить шлях до супутника на геостаціонарній орбіті і назад, займає приблизно 0,25 секунди на весь шлях.

Архітектура приймачів¶

На малюнку в розділі “Приймач” показано, як вхідний сигнал перетворюється і розділяється на I і Q. Така схема називається “пряме перетворення”, або “нульова ПЧ”, тому що радіочастоти безпосередньо перетворюються до базової смуги частот. Інший варіант - взагалі не перетворювати частоти вниз і робити вибірку так швидко, щоб захопити все від 0 Гц до 1/2 частоти дискретизації. Ця стратегія називається “пряма вибірка” або “пряма ВЧ”, і вона вимагає надзвичайно дорогого чіпа АЦП. Третя архітектура, популярна тому, що саме так працювали старі радіоприймачі, відома як “супергетеродин”. Вона передбачає перетворення вниз, але не до 0 Гц. Він поміщає сигнал, що нас цікавить, на проміжну частоту, відому як “ПЧ”. Підсилювач з низьким рівнем шуму (LNA) - це просто підсилювач, призначений для сигналів надзвичайно низької потужності на вході. Ось блок-схеми цих трьох архітектур, зверніть увагу, що існують також варіації та гібриди цих архітектур:

Три найпоширеніші архітектури приймачів: пряма дискретизація, пряме перетворення та супергетеродин

Сигнали основної та смугових частот¶

Ми називаємо сигнал з центром близько 0 Гц “основною смугою”. І навпаки, “смуговий” означає, що сигнал існує на певній радіочастоті, не близькій до 0 Гц, яка була зміщена вгору з метою бездротової передачі. Поняття “передача в основній смузі частот” не існує, тому що ви не можете передати щось уявне. Сигнал в основній смузі може бути ідеально відцентрований на 0 Гц, як на правій частині малюнка в попередньому розділі. Він може бути близько 0 Гц, як два сигнали, показані нижче. Ці два сигнали все ще вважаються основною смугою. Також показано приклад смугового сигналу з центром на дуже високій частоті, позначеній $f_c$ .

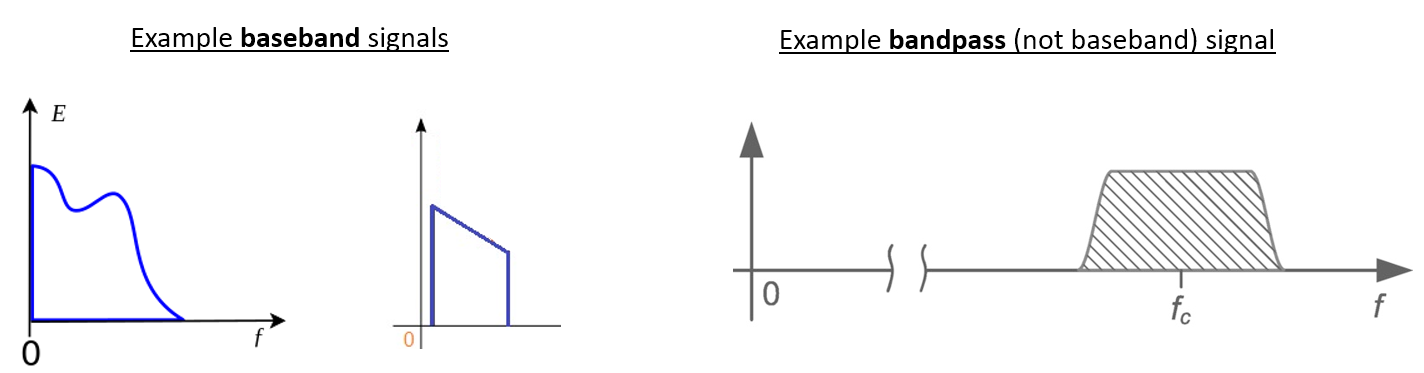
Ви також можете почути термін “проміжна частота” (скорочено ПЧ); поки що уявіть собі ПЧ як проміжний крок перетворення у радіоприймачі між базовою смугою та смугою пропускання/ВЧ.

Ми, як правило, створюємо, записуємо або аналізуємо сигнали в базовій смузі, оскільки можемо працювати з меншою частотою дискретизації (з причин, описаних у попередньому підрозділі). Важливо зазначити, що сигнали базової смуги часто є складними сигналами, в той час як сигнали в смузі пропускання (наприклад, сигнали, які ми фактично передаємо через радіочастоти) є реальними. Подумайте про це: оскільки сигнал, що подається через антену, повинен бути реальним, ви не можете безпосередньо передавати складний/уявний сигнал. Ви знатимете, що сигнал точно є комплексним, якщо від’ємна та додатна частоти сигналу не збігаються в точності. Зрештою, комплексні числа - це те, як ми представляємо від’ємні частоти. Насправді не існує від’ємних частот; це просто частина сигналу нижче несучої частоти.

У попередньому розділі, де ми гралися з комплексною точкою 0,7 - 0,4j, це був, по суті, один відлік у сигналі основної смуги. Більшість часу, коли ви бачите комплексні відліки (IQ-відліки), ви перебуваєте в основній смузі частот. Сигнали рідко представляються або зберігаються в цифровому вигляді в радіочастотному діапазоні через велику кількість даних, а також через те, що нас зазвичай цікавить лише невелика частина радіочастотного спектру.

Налаштування стрибкоподібного та зміщеного постійного струму¶

Як тільки ви починаєте працювати з SDR, ви часто бачите великий пік в центрі БПФ. Це називається “зміщенням постійного струму” або “стрибком постійного струму”, або іноді “витоком LO”, де LO означає локальний осцилятор.

Ось приклад стрибка постійного струму:

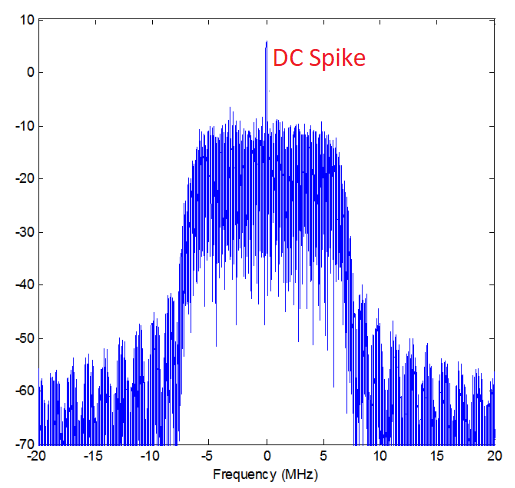
Пік постійного струму, показаний у спектральній щільності потужності (PSD)

Оскільки SDR налаштовується на центральну частоту, ділянка 0 Гц у БПФ відповідає центральній частоті. При цьому стрибок постійного струму не обов’язково означає, що на центральній частоті є енергія. Якщо є лише стрибок постійного струму, а решта БПФ виглядає як шум, то, швидше за все, там, де він вам показує, насправді немає сигналу.

Зміщення постійного струму є поширеним артефактом у приймачах прямого перетворення, які використовують архітектуру SDR, таких як PlutoSDR, RTL-SDR, LimeSDR і багатьох Ettus USRP. У приймачах прямого перетворення генератор, LO, перетворює сигнал з його фактичної частоти в базову смугу. В результаті, витоки від цього генератора з’являються в центрі смуги пропускання, що спостерігається. Витоки LO - це додаткова енергія, створена комбінацією частот. Видалити цей додатковий шум важко, оскільки він близький до бажаного вихідного сигналу. Багато радіочастотних інтегральних схем (RFIC) мають вбудовану функцію автоматичного видалення постійного зсуву, але для її роботи зазвичай потрібен сигнал. Ось чому стрибок постійного струму буде дуже помітним за відсутності сигналу.

Швидкий спосіб впоратися зі зміщенням постійного струму - передискретизувати сигнал і розстроїти його. Для прикладу, скажімо, ми хочемо переглянути 5 МГц спектра на частоті 100 МГц. Замість цього ми можемо зробити вибірку на 20 МГц з центральною частотою 95 МГц.

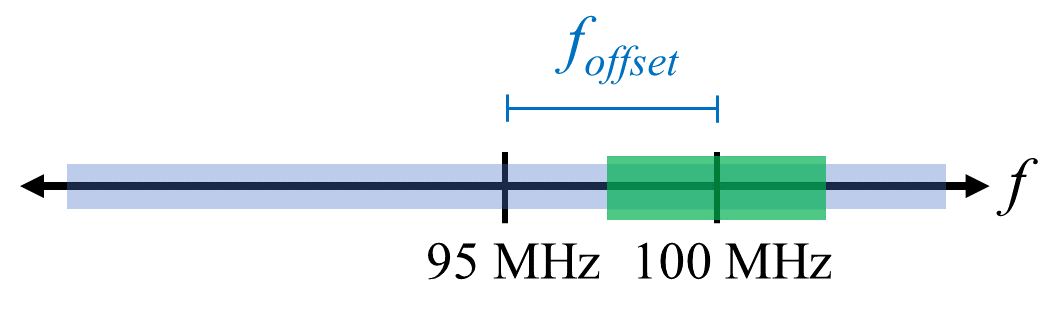
Процес налаштування зсуву для уникнення стрибка постійного струму

Синя рамка вище показує, що насправді виділяється SDR, а зелена рамка відображає частину спектру, яку ми хочемо отримати. Наш LO буде встановлено на 95 МГц, тому що це частота, на яку ми просимо SDR налаштуватися. Оскільки 95 МГц знаходиться за межами зеленого квадратика, ми не отримаємо жодного сплеску постійного струму.

Є одна проблема: якщо ми хочемо, щоб наш сигнал був центрований на 100 МГц і містив лише 5 МГц, нам доведеться самостійно виконати зсув частоти, фільтрацію і пониження дискретизації сигналу (про це ми дізнаємося пізніше). На щастя, цей процес розстроювання, так зване застосування LO-зсуву, часто вбудовано в SDR, де вони автоматично виконують розстроювання, а потім зміщують частоту до бажаної центральної частоти. Ми виграємо, коли SDR може робити це самостійно: нам не потрібно передавати вищу частоту дискретизації через USB- або Ethernet-з’єднання, які обмежують можливості використання високої частоти дискретизації.

Цей підрозділ, присвячений зміщенням постійного струму, є гарним прикладом того, чим цей підручник відрізняється від інших. У середньостатистичному підручнику з ЦОС обговорюється дискретизація, але в ньому, як правило, не розглядаються перешкоди при реалізації, такі як зміщення постійного струму, незважаючи на їхню поширеність на практиці.

Семплірування за допомогою нашого SDR¶

Для отримання специфічної для SDR інформації про виконання дискретизації див. одну з наступних глав:

PlutoSDR на Python Розділ
USRP на Python Глава

Обчислення середньої потужності¶

У радіочастотному DSP ми часто хочемо обчислити потужність сигналу, наприклад, щоб виявити наявність сигналу перед тим, як намагатися виконати подальшу обробку. Для дискретного складного сигналу, тобто сигналу, який ми дискретизували, ми можемо знайти середню потужність, взявши величину кожного відліку, піднісши її до квадрата і знайшовши середнє значення:

$P = \frac{1}{N} \sum_{n=1}^{N} |x[n]|^2$

Пам’ятайте, що абсолютне значення комплексного числа - це просто величина, тобто $\sqrt{I^2+Q^2}$

У мові Python обчислення середнього степеня буде мати вигляд:

avg_pwr = np.mean(np.abs(x)**2)

Це дуже корисний трюк для обчислення середньої потужності дискретизованого сигналу. Якщо ваш сигнал має приблизно нульове середнє значення - що зазвичай буває в SDR (пізніше ми побачимо чому) - то потужність сигналу можна знайти, взявши дисперсію відліків. За цих обставин ви можете обчислити потужність таким чином у Python:

avg_pwr = np.var(x) # (сигнал повинен мати приблизно нульове середнє)

Причина, чому дисперсія вибірок обчислює середню потужність, досить проста: рівняння для дисперсії має вигляд $\frac{1}{N}\sum^N_{n=1} |x[n]-\mu|^2$ де $\mu$ - середнє значення сигналу. Це рівняння виглядає знайомим! Якщо $\mu$ дорівнює нулю, то рівняння для визначення дисперсії відліків стає еквівалентним рівнянню для потужності. Ви також можете відняти середнє значення від вибірок у вашому вікні спостережень, а потім взяти дисперсію. Просто знайте, що якщо середнє значення не дорівнює нулю, то дисперсія і потужність не рівні.

Обчислення спектральної щільності потужності¶

У попередньому розділі ми дізналися, що можна перетворити сигнал у частотну область за допомогою ШПФ, а результат називається спектральною щільністю потужності (PSD). PSD є надзвичайно корисним інструментом для візуалізації сигналів у частотній області, і багато алгоритмів ЦОС виконуються в частотній області. Але для того, щоб дійсно знайти PSD пачки відліків і побудувати її графік, ми робимо більше, ніж просто беремо БПФ. Для обчислення PSD потрібно виконати наступні шість операцій:

Беремо БПФ наших відліків. Якщо у нас є x відліків, то за замовчуванням розмір БПФ буде дорівнювати довжині x. Давайте використаємо перші 1024 відліки як приклад для створення ШПФ розміром 1024. На виході ми отримаємо 1024 комплексних числа з плаваючою комою.
Візьмемо величину виходу ШПФ, яка дає нам 1024 дійсних числа.
Піднесіть отриману величину до квадрату, щоб отримати потужність.
Нормалізуємо: ділимо на розмір ШПФ ( $N$ ) і частоту дискретизації ( $Fs$ ).
Конвертуємо в дБ за допомогою $10 \log_{10}()$ ; ми завжди переглядаємо PSD в логарифмічній шкалі.
Виконайте зсув ШПФ, описаний у попередньому розділі, щоб перемістити “0 Гц” у центр, а від’ємні частоти - ліворуч від центру.

Ці шість кроків у Python виглядають так:

Fs = 1e6 # скажімо, ми зробили вибірку на частоті 1 МГц
# припустимо, що x містить ваш масив відліків IQ
N = 1024
x = x[0:N] # ми візьмемо ШПФ тільки перших 1024 відліків, див. текст нижче
PSD = np.abs(np.fft.fft(x))**2 / (N*Fs)
PSD_log = 10.0*np.log10(PSD)
PSD_shifted = np.fft.fftshift(PSD_log)

За бажанням ми можемо застосувати вікно, про яке ми дізналися у розділі Частотний домен. Вікно з’явиться безпосередньо перед рядком коду з fft().

# додати наступний рядок після виконання x = x[0:1024]
x = x * np.hamming(len(x)) # застосовуємо вікно Хеммінга

Для побудови цієї PSD нам потрібно знати значення осі x. Як ми дізналися з попереднього розділу, коли ми робимо вибірку сигналу, ми “бачимо” лише спектр між -Fs/2 і Fs/2, де Fs - це частота дискретизації. Роздільна здатність, якої ми досягаємо в частотній області, залежить від розміру нашого ШПФ, який за замовчуванням дорівнює кількості відліків, над якими ми виконуємо операцію ШПФ. У цьому випадку наша вісь х - це 1024 рівномірно розташовані точки між -0,5 МГц і 0,5 МГц. Якби ми налаштували наш SDR на 2,4 ГГц, наше вікно спостереження було б між 2,3995 ГГц і 2,4005 ГГц. У Python зміщення вікна спостереження буде виглядати так:

center_freq = 2.4e9 # частота, на яку ми налаштували наш SDR
f = np.arange(Fs/-2.0, Fs/2.0, Fs/N) # старт, стоп, крок. з центром навколо 0 Гц
f += center_freq # тепер додаємо центральну частоту
plt.plot(f, PSD_shifted)
plt.show()

У нас повинен залишитися гарний PSD!

Якщо ви хочете знайти PSD для мільйонів відліків, не робіть ШПФ з мільйонами точок, тому що це займе вічність. Зрештою, це дасть вам на виході мільйон “частотних бінів”, що занадто багато, щоб показати на графіку. Замість цього я пропоную зробити кілька менших PSD і усереднити їх разом або відобразити за допомогою графіка спектрограми. Крім того, якщо ви знаєте, що ваш сигнал не змінюється швидко, достатньо використати кілька тисяч відліків і знайти PSD з них; за цей часовий проміжок у кілька тисяч відліків ви, ймовірно, захопите достатньо сигналу, щоб отримати гарне представлення.

Ось повний приклад коду, який включає генерування сигналу (комплексна експонента з частотою 50 Гц) і шуму. Зверніть увагу, що N, кількість відліків для імітації, стає довжиною ШПФ, оскільки ми беремо ШПФ всього імітованого сигналу.

import numpy as np
import matplotlib.pyplot as plt

Fs = 300 # частота дискретизації
Ts = 1/Fs # період дискретизації
N = 2048 # кількість відліків для моделювання

t = Ts*np.arange(N)
x = np.exp(1j*2*np.pi*50*t) # імітує синусоїду 50 Гц

n = (np.random.randn(N) + 1j*np.random.randn(N))/np.sqrt(2) # комплексний шум з одиничною потужністю
noise_power = 2
r = x + n * np.sqrt(noise_power)

PSD = np.abs(np.fft.fft(r))**2 / (N*Fs)
PSD_log = 10.0*np.log10(PSD)
PSD_shifted = np.fft.fftshift(PSD_log)

f = np.arange(Fs/-2.0, Fs/2.0, Fs/N) # старт, стоп, крок

plt.plot(f, PSD_shifted)
plt.xlabel("Частота [Гц]")
plt.ylabel("Амплітуда [дБ]")
plt.grid(True)
plt.show()

Виведення на екран:

Подальше читання¶

http://rfic.eecs.berkeley.edu/~niknejad/ee242/pdf/eecs242_lect3_rxarch.pdf