12. Codificación de canal

En este capítulo presentamos los conceptos básicos de codificación de canales, también conocido como Forward Error Correction (FEC), el límite de Shannon, los códigos Hamming, los turbo códigos y los códigos LDPC. La codificación de canal es un área enorme dentro de las comunicaciones inalámbricas y es una rama de la “teoría de la información”, que es el estudio de la cuantificación, almacenamiento y comunicación de la información.

¿Por qué necesitamos codificación de canales?

Como aprendimos en el capitulo Ruido y dB, los canales inalámbricos son ruidosos y los símbolos transmitidos no llegan perfectamente al receptor. Si ha realizado un curso de redes, es posible que ya conozca las comprobaciones de redundancia cíclica (CRC), las cuales detectan errores en el receptor final. El propósito de la codificación de canales es detectar y corregir errores en el receptor. Si dejamos cierto margen de error, entonces podremos transmitir con un esquema de modulación de orden superior, por ejemplo, sin tener un enlace roto. Como ejemplo visual, considere las siguientes constelaciones que muestran QPSK (izquierda) y 16QAM (derecha) bajo la misma cantidad de ruido. QPSK proporciona 2 bits por símbolo, mientras que 16QAM es el doble de la velocidad de datos a 4 bits por símbolo. Pero observe cómo en la constelación QPSK los símbolos tienden a no pasar el límite de decisión del símbolo, o el eje x y el eje y, lo que significa que los símbolos se recibirán correctamente. Mientras tanto, en el gráfico 16QAM, hay superposición en los grupos y, como resultado, habrá muchos símbolos recibidos incorrectamente.

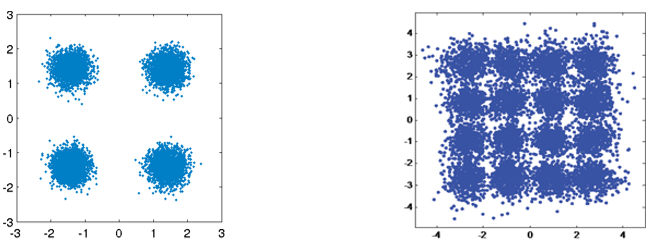
Un CRC fallido generalmente resulta en una retransmisión, al menos cuando se usa un protocolo como TCP. Si Alice le está enviando un mensaje a Bob, preferiríamos no tener que hacer que Bob le envíe un mensaje a Alice solicitando la información nuevamente. El propósito de la codificación de canales es transmitir redundancia de la información. La redundancia es un mecanismo de seguridad que reduce la cantidad de paquetes erróneos, retransmisiones o datos perdidos.

Discutimos por qué necesitamos codificación de canal, así que veamos dónde ocurre en la cadena de transmisión-recepción:

Observe que hay múltiples pasos de codificación en la cadena de transmisión-recepción. La codificación fuente, es nuestro primer paso, no es lo mismo que la codificación de canal; La codificación de fuente está destinada a comprimir los datos que se transmitirán tanto como sea posible, al igual que cuando se comprime un archivo para reducir el espacio ocupado. Es decir, la salida del bloque de codificación de origen debe ser más pequeña que la entrada de datos, pero la salida de la codificación del canal será mayor que su entrada porque se agrega redundancia.

Tipos de Códigos

Para realizar la codificación de canal utilizamos un “código de corrección de errores”. Este código nos dice, dados los bits que tenemos que transmitir, ¿qué bits transmitimos realmente? El código más básico se llama “codificación de repetición”, y es cuando simplemente repites un bit N veces seguidas. Para el código de repetición 3, se transmitiría cada bit tres veces:

• 0 → 000
• 1 → 111

El mensaje 10010110 se transmite como 111000000111000111111000 después de la codificación del canal.

Algunos códigos funcionan en “bloques” de bits de entrada, mientras que otros utilizan un enfoque de flujo. Los códigos que funcionan en bloques con datos de una longitud definida, se denominan “códigos de bloque”, mientras que los códigos que funcionan en un flujo de bits, donde la longitud de los datos es arbitraria, se denominan “códigos convolucionales”. Estos son los dos tipos principales de códigos. Nuestro código de repetición 3 es un código de bloque donde cada bloque tiene tres bits.

Además, estos códigos de corrección de errores no se utilizan únicamente en la codificación de canales para enlaces inalámbricos. ¿Alguna vez almacenó información en un disco duro o SSD y se preguntó cómo es posible que nunca haya errores de bits al volver a leer la información? Escribir y luego leer de memoria es similar a un sistema de comunicación. Los controladores de disco duro/SSD tienen corrección de errores incorporada. Es transparente para el sistema operativo y puede ser propietario ya que todo está integrado en el disco duro/SSD. Para medios portátiles como CD, la corrección de errores debe estar estandarizada. Los códigos Reed-Solomon eran comunes en los CD-ROM.

Code-Rate

Toda corrección de errores incluye alguna forma de redundancia. Eso significa que si queremos transmitir 100 bits de información, tendremos que enviar más de 100 bits. “code-rate” es la relación entre el número de bits de información y el número total de bits enviados (es decir, información más bits de redundancia). Volviendo al ejemplo de codificación de repetición 3, si tengo 100 bits de información, podemos determinar lo siguiente:

• 300 bits son enviados
• Únicamente 100 bits representan la información
• Code-rate = 100/300 = 1/3

El code-rate siempre será menor que 1, ya que existe un equilibrio entre redundancia y rendimiento. Un code-rate más baja significa más redundancia y menos rendimiento.

Modulación y codificación

En el capitulo Modulación Digital abordamos el ruido en esquemas de modulación. Con una SNR baja, necesita un esquema de modulación de orden bajo (por ejemplo, QPSK) para lidiar con el ruido, y con una SNR alta puede usar modulación como 256QAM para obtener más bits por segundo. La codificación de canales es la misma; desea velocidades de código más bajas con SNR bajas, y con SNR altas puede usar una velocidad de código de casi 1. Los sistemas de comunicaciones modernos tienen un conjunto de esquemas combinados de modulación y codificación, llamados MCS. Cada MCS especifica un esquema de modulación y un esquema de codificación que se utilizarán en niveles SNR específicos.

Las comunicaciones modernas cambian de forma adaptativa el MCS en tiempo real según las condiciones del canal inalámbrico. El receptor envía información sobre la calidad del canal al transmisor. Se deben compartir comentarios antes de que cambie la calidad del canal inalámbrico, lo que podría ser del orden de mili segundos (ms). Este proceso adaptativo conduce a comunicaciones con el mayor rendimiento posible y es utilizado por tecnologías modernas como LTE, 5G y WiFi. A continuación se muestra una visualización de una torre de telefonía móvil que cambia el MCS durante la transmisión a medida que cambia la distancia del usuario a la célula.

Cuando se utiliza MCS adaptativo, si se grafica el rendimiento sobre la SNR, se obtiene una curva en forma de escalera como la del siguiente gráfico. Los protocolos como LTE suelen tener una tabla que indica qué MCS debe usarse y en qué SNR.

Codigo Hamming

Veamos códigos de corrección de errores simples. El Código Hamming fue el primer código no trivial desarrollado. A finales de la década de 1940, Richard Hamming trabajaba en los Laboratorios Bell, utilizando una computadora electromecánica que utilizaba cinta de papel perforada. Cuando se detectaran errores en la máquina, ésta se detendría y los operadores tendrían que arreglarlos. Hamming se sintió frustrado por tener que reiniciar sus programas desde cero debido a errores detectados. Dijo: “Maldita sea, si la máquina puede detectar un error, ¿por qué no puede localizar la posición del error y corregirlo?”. Pasó los siguientes años desarrollando el Código Hamming para que la computadora pudiera hacer exactamente eso.

En los códigos Hamming, se agregan bits adicionales, llamados bits de paridad o bits de verificación, a la información para lograr redundancia. Todas las posiciones de bits que son potencias de dos son bits de paridad: 1, 2, 4, 8, etc. Las otras posiciones de bits son para información. La tabla debajo de este párrafo resalta los bits de paridad en verde. Cada bit de paridad “cubre” todos los bits donde el AND bit a bit de la paridad y la posición del bit no son cero, marcados con una X roja debajo. Si queremos utilizar un bit de datos, necesitamos los bits de paridad que lo cubren. Para poder subir al bit de datos d9, necesitamos el bit de paridad p8 y todos los bits de paridad que le preceden, por lo que esta tabla nos indica cuántos bits de paridad necesitamos para una determinada cantidad de bits. Este patrón continúa indefinidamente.

Los códigos Hamming son códigos de bloque, por lo que operan con N bits de datos a la vez. Entonces, con tres bits de paridad podemos operar en bloques de cuatro bits de datos a la vez. Representamos este esquema de codificación de errores como Hamming(7,4), donde el primer argumento son los bits totales transmitidos y el segundo argumento son los bits de datos.

Las siguientes son tres propiedades importantes de los códigos Hamming:

• El número mínimo de cambios de bits necesarios para pasar de cualquier palabra de código a cualquier otra palabra de código es tres
• Puede corregir errores de un bit.
• Puede detectar pero no corregir errores de dos bits.

Algorítmicamente, el proceso de codificación se puede realizar mediante una multiplicación matricial simple, utilizando lo que se denomina “matriz generadora”. En el siguiente ejemplo, el vector 1011 son los datos a codificar, es decir, la información que queremos enviar al receptor. La matriz 2D es la matriz generadora y define el esquema de código. El resultado de la multiplicación proporciona la palabra clave a transmitir.

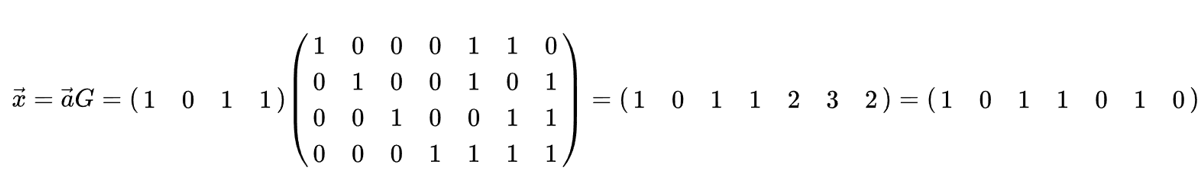
El objetivo de profundizar en los códigos Hamming era dar una idea de cómo funciona la codificación de errores. Los códigos de bloque tienden a seguir este tipo de patrón. Los códigos convolucionales funcionan de manera diferente, pero no entraremos en detalles aquí; a menudo utilizan decodificación estilo Trellis, que se puede mostrar en un diagrama similar a este:

Decodificación Soft vs Hard

Recuerde que en el receptor la demodulación se produce antes de la decodificación. El demodulador puede decirnos su mejor estimación sobre qué símbolo se envió, o puede generar el valor “soft”. Para BPSK, en lugar de decirnos 1 o 0, el demodulador puede decir 0,3423 o -1,1234, cualquiera que sea el valor “soft” del símbolo. Normalmente, la decodificación está diseñada para utilizar valores hard o soft.

• Soft decision decoding – usa los valores soft
• Hard decision decoding – usa únicamente el 1’s y el 0’s

El software es más robusto porque utiliza toda la información a su disposición, pero también es mucho más complicado de implementar. Los códigos Hamming de los que hablamos usaban decisiones hard, mientras que los códigos convolucionales tienden a usar decisiones soft.

Limite de Shannon

El límite de Shannon o capacidad de Shannon es una teoría increíble que nos dice cuántos bits por segundo de información libre de errores podemos enviar:

• C – Capacidad de Canal [bits/sec]
• B – Ancho de Banda del canal [Hz]
• S – Potencia promedio de la señal recivida [watts]
• N – Potencia promedio del ruido [watts]

Esta ecuación representa lo mejor que puede hacer cualquier MCS cuando opera a una SNR lo suficientemente alta como para estar libre de errores. Tiene más sentido trazar el límite en bits/seg/Hz, es decir, bits/seg por cantidad de espectro:

con SNR en términos lineales (no dB). Sin embargo, al trazarlo, generalmente representamos la SNR en dB por conveniencia:

Si ve los gráficos de los límites de Shannon en otros lugares que se ven un poco diferentes, probablemente estén usando un eje x de “energía por bit” o , que no es más que una alternativa al trabajo en SNR.

Podría ayudar a simplificar las cosas darse cuenta de que cuando la SNR es bastante alta (por ejemplo, 10 dB o más), el límite de Shannon se puede aproximar como , que es aproximadamente (explained here). Por ejemplo, a 24 dB SNR estás viendo 8 bits/seg/Hz, por lo que si tienes 1 MHz para usar, son 8 Mbps. Podrías estar pensando, “bueno, ese es sólo el límite teórico”, pero las comunicaciones modernas se acercan bastante a ese límite, por lo que, como mínimo, te da una aproximación aproximada. Siempre puede reducir ese número a la mitad para tener en cuenta la sobrecarga de paquetes/tramas y el MCS no ideal.

El rendimiento máximo de WiFi 802.11n que funciona en la banda de 2,4 GHz (que utiliza canales de 20 MHz de ancho), según las especificaciones, es de 300 Mbps. Obviamente, podría sentarse justo al lado de su enrutador y obtener una SNR extremadamente alta, tal vez 60 dB, pero para ser confiable/práctico, es poco probable que el MCS de rendimiento máximo (recuerde la curva de escalera desde arriba) requiera una SNR tan alta. Incluso puedes echarle un vistazo a MCS list for 802.11n. 802.11n llega hasta 64-QAM y, combinado con la codificación de canales, requiere una SNR de alrededor de 25 dB según this table. Eso significa que incluso a 60 dB SNR tu WiFi seguirá usando 64-QAM. Entonces, a 25 dB, el límite de Shannon es aproximadamente 8,3 bits/seg/Hz, lo que, dados 20 MHz de espectro, es 166 Mbps. Sin embargo, cuando se tiene en cuenta MIMO, que cubriremos en un capítulo futuro, se pueden ejecutar cuatro de esas transmisiones en paralelo, lo que da como resultado 664 Mbps. Si reduce ese número a la mitad, obtendrá algo muy cercano a la velocidad máxima anunciada de 300 Mbps para WiFi 802.11n en la banda de 2,4 GHz.

La prueba detrás del límite de Shannon es bastante loca; Se trata de matemáticas que se ven así:

Para más información, ver here.

Códigos de última generación

Actualmente, los mejores esquemas de codificación de canales son:

1. Turbo códigos, utilizados en 3G, 4G, la nave espacial de la NASA.
2. Códigos LDPC, utilizados en DVB-S2, WiMAX, IEEE 802.11n.

Ambos códigos se acercan al límite de Shannon (es decir, casi lo alcanzan bajo ciertas SNR). Los códigos Hamming y otros códigos más simples no se acercan al límite de Shannon. Desde el punto de vista de la investigación, no queda mucho margen de mejora en cuanto a los propios códigos. La investigación actual se centra más en hacer que la decodificación sea más eficiente desde el punto de vista computacional y adaptable a la retroalimentación del canal.

Low-density parity-check (LDPC) son una clase de códigos de bloques lineales altamente eficientes. Fueron presentados por primera vez por Robert G. Gallager en su tesis doctoral en 1960 en el MIT. Debido a la complejidad computacional en su implementación, ¡fueron ignorados hasta la década de 1990! Tiene 89 años al momento de escribir este artículo (2020), todavía está vivo y ha ganado muchos premios por su trabajo (décadas después de haberlo hecho). LDPC no está patentado y, por lo tanto, es de uso gratuito (a diferencia de los códigos turbo), por lo que se utilizó en muchos protocolos abiertos.

Los turbo códigos se basan en códigos convolucionales. Es una clase de código que combina dos o más códigos convolucionales más simples y un entrelazador. La solicitud de patente fundamental para turbo códigos se presentó el 23 de abril de 1991. Los inventores eran franceses, por lo que cuando Qualcomm quiso utilizar turbo códigos en CDMA para 3G, tuvo que crear un acuerdo de licencia de patente con France Telecom. La patente principal expiró el 29 de agosto de 2013.