10. Filtros¶

En este capítulo aprendemos sobre los filtros digitales usando Python. Cubrimos los tipos de filtros (FIR/IIR y paso bajo/paso alto/paso de banda/parada de banda), cómo se representan los filtros digitalmente y cómo se diseñan. Terminamos con una introducción al pulse shaping, que exploraremos más a fondo en el capitulo Formador de Pulso .

Filtros Básicos¶

Los filtros se utilizan en muchas disciplinas. Por ejemplo, el procesamiento de imágenes se hace uso intensivo de filtros 2D, donde la entrada y la salida son imágenes. Puedes usar un filtro todas las mañanas para preparar tu café, que filtra los sólidos del líquido. En DSP, los filtros se utilizan principalmente para:

Separación de señales que se han combinado (por ejemplo, extraer la señal que desea)
Eliminación del exceso de ruido después de recibir una señal.
Restauración de señales que han sido distorsionadas de alguna manera (por ejemplo, un ecualizador de audio es un filtro)

Ciertamente, existen otros usos para los filtros, pero este capítulo está destinado a presentar el concepto en lugar de explicar todas las formas en que se puede realizar el filtrado.

Quizás pienses que sólo nos importan los filtros digitales; después de todo, este libro de texto explora DSP. Sin embargo, es importante saber que muchos filtros serán analógicos, como los de nuestros SDR colocados antes del convertidor analógico a digital (ADC) en el lado de recepción. La siguiente imagen yuxtapone un esquema de un circuito de filtro analógico con una representación de diagrama de flujo de un algoritmo de filtrado digital.

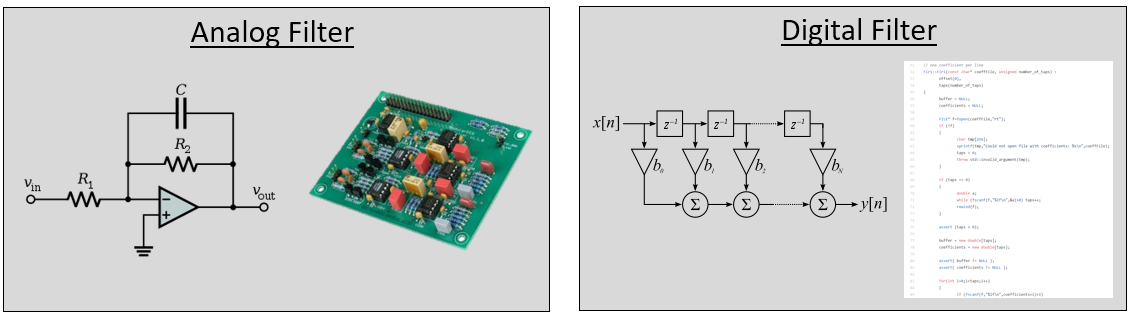
En DSP, donde la entrada y la salida son señales, un filtro tiene una señal de entrada y una señal de salida:

Figure made with TikZ

No se pueden introducir dos señales diferentes en un solo filtro sin sumarlas primero o realizar alguna otra operación. Del mismo modo, la salida siempre será una señal, es decir, una matriz 1D de números.

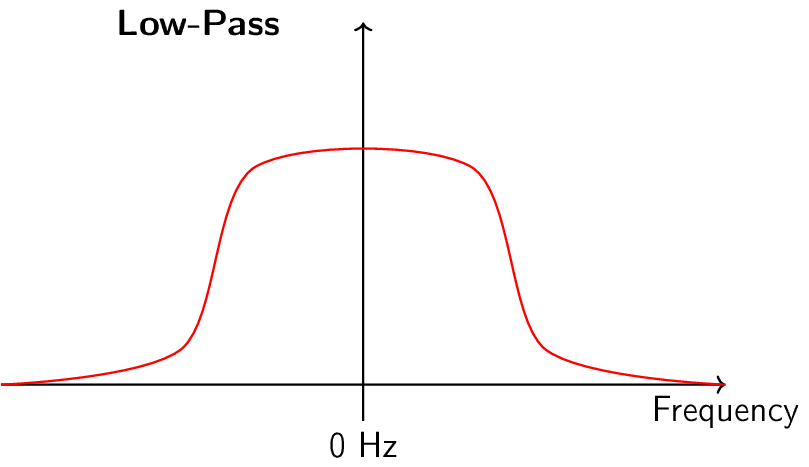
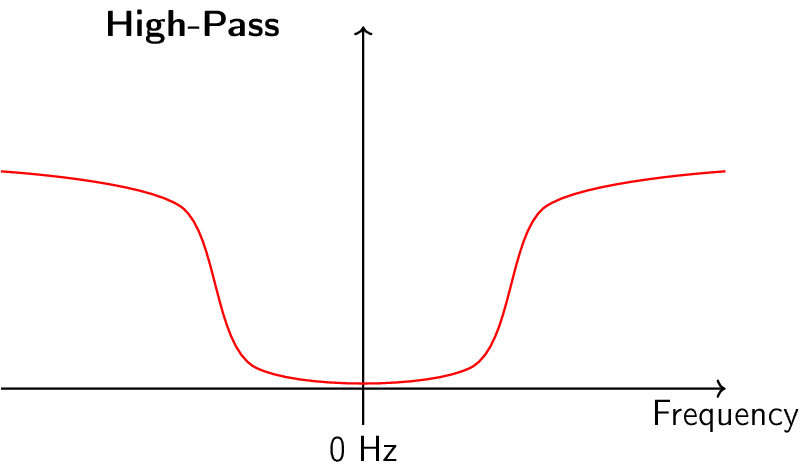
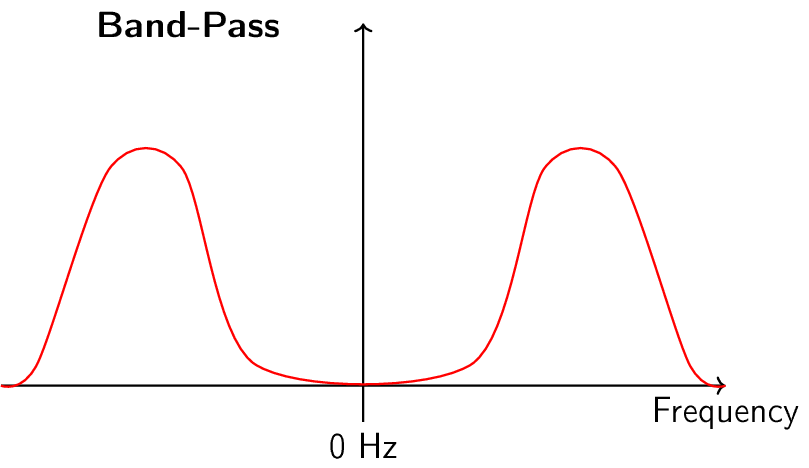
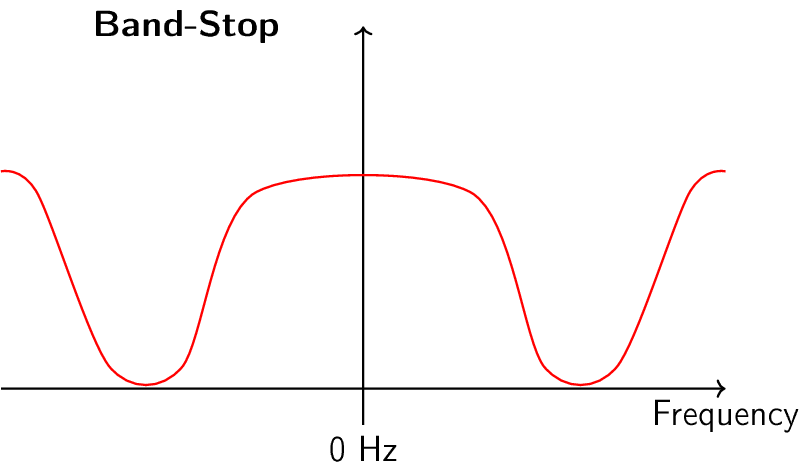
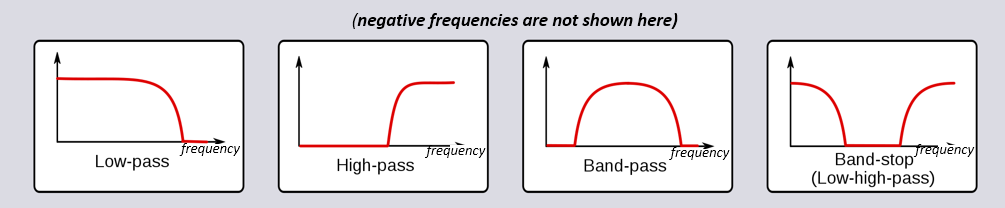
Hay cuatro tipos básicos de filtros: paso bajo, paso alto, paso banda y supresión de banda. Cada tipo modifica las señales para centrarse en diferentes rangos de frecuencias dentro de ellas. Los gráficos a continuación demuestran cómo se filtran las frecuencias en las señales para cada tipo, presentándose primero solo con frecuencias positivas (más fáciles de entender) y luego incluyendo también las negativas.

Filter types, including low-pass, high-pass, band-pass, and band-stop filtering in the frequency domain

Cada filtro permite que ciertas frecuencias permanezcan en una señal mientras bloquea otras frecuencias. El rango de frecuencias que deja pasar un filtro se conoce como “banda de paso” y “banda de parada” se refiere a lo que está bloqueado. En el caso del filtro de paso bajo, deja pasar las frecuencias bajas y detiene las altas, por lo que 0 Hz siempre estará en la banda de paso. Para un filtro de paso alto y de paso de banda, 0 Hz siempre estará en la banda de parada.

No confunda estos tipos de filtrado con la implementación algorítmica de filtrado (por ejemplo, IIR vs FIR). El tipo más común, con diferencia, es el filtro de paso bajo (LPF), porque a menudo representamos señales en banda base. LPF nos permite filtrar todo lo que está “alrededor” de nuestra señal, eliminando el exceso de ruido y otras señales.

Representación del Filtro¶

Para la mayoría de los filtros que veremos (conocidos como filtros de tipo FIR, o respuesta de impulso finito), podemos representar el filtro en sí con una única matriz con datos tipo float. Para filtros simétricos en el dominio de la frecuencia, estos datos float serán reales (en lugar de complejos) y tiende a haber un número impar de ellos. A este conjunto de float lo llamamos “Filter Taps”. A menudo utilizamos $h$ como símbolo para los filter taps. A continuación se muestra un ejemplo de un conjunto de filter taps, que definen un filtro:

h =  [ 9.92977939e-04  1.08410297e-03  8.51595307e-04  1.64604862e-04
 -1.01714338e-03 -2.46268845e-03 -3.58236429e-03 -3.55412543e-03
 -1.68583512e-03  2.10562324e-03  6.93100252e-03  1.09302641e-02
  1.17766532e-02  7.60955496e-03 -1.90555639e-03 -1.48306750e-02
 -2.69313236e-02 -3.25659606e-02 -2.63400086e-02 -5.04184562e-03
  3.08099470e-02  7.64264738e-02  1.23536693e-01  1.62377258e-01
  1.84320776e-01  1.84320776e-01  1.62377258e-01  1.23536693e-01
  7.64264738e-02  3.08099470e-02 -5.04184562e-03 -2.63400086e-02
 -3.25659606e-02 -2.69313236e-02 -1.48306750e-02 -1.90555639e-03
  7.60955496e-03  1.17766532e-02  1.09302641e-02  6.93100252e-03
  2.10562324e-03 -1.68583512e-03 -3.55412543e-03 -3.58236429e-03
 -2.46268845e-03 -1.01714338e-03  1.64604862e-04  8.51595307e-04
  1.08410297e-03  9.92977939e-04]

Ejemplo de caso de uso¶

Para aprender cómo se usan los filtros, veamos un ejemplo en el que sintonizamos nuestro SDR a la frecuencia de una señal existente que queremos aislarlo de otras señales. Recuerde que le decimos a nuestro SDR qué frecuencia sintonizar, pero las muestras que captura el SDR están en banda base, lo que significa que la señal se mostrará centrada alrededor de 0 Hz. Tendremos que realizar un seguimiento de qué frecuencia le indicamos al SDR que sintonice. Esto es lo que podríamos recibir:

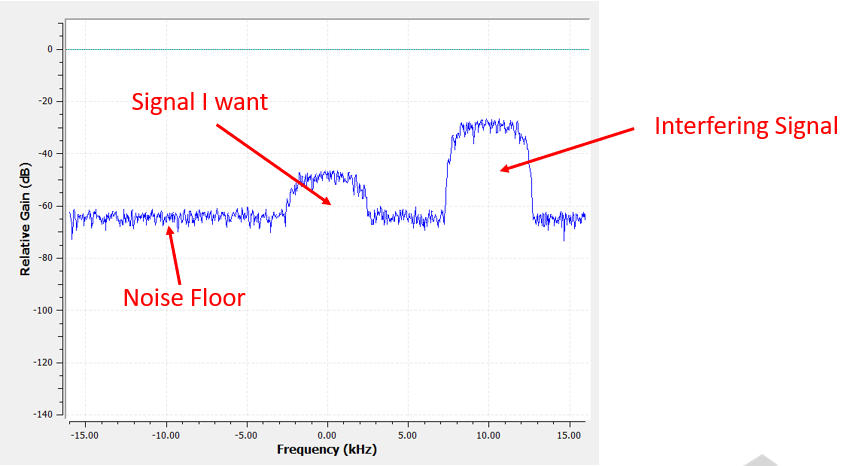
GNU Radio frequency domain plot of signal of interest and an interfering signal and noise floor

Como nuestra señal ya está centrada en DC (0 Hz), sabemos que queremos un filtro paso bajo. Debemos elegir una “frecuencia de corte” (también conocida como frecuencia de esquina), que determinará cuándo la banda de paso pasa a banda de parada. La frecuencia de corte siempre estará en unidades de Hz. En este ejemplo, 3 kHz parece un buen valor:

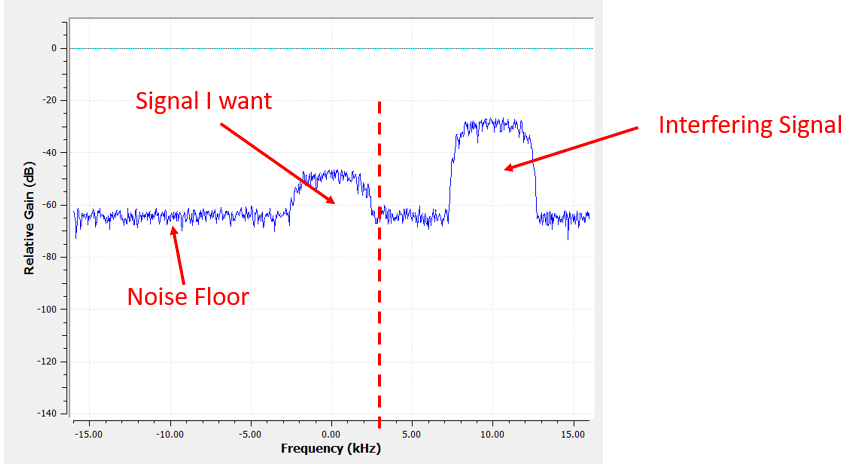
Sin embargo, tal como funcionan la mayoría de los filtros paso bajo, el límite de frecuencia negativo también será -3 kHz. Es decir, es simétrico alrededor de DC (más adelante verás por qué). Nuestras frecuencias de corte se verán así (la banda de paso es el área intermedia):

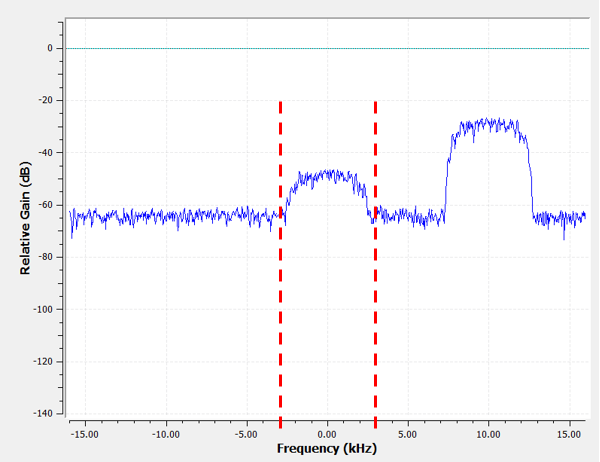
Después de crear y aplicar el filtro con una frecuencia de corte de 3 kHz, ahora tenemos:

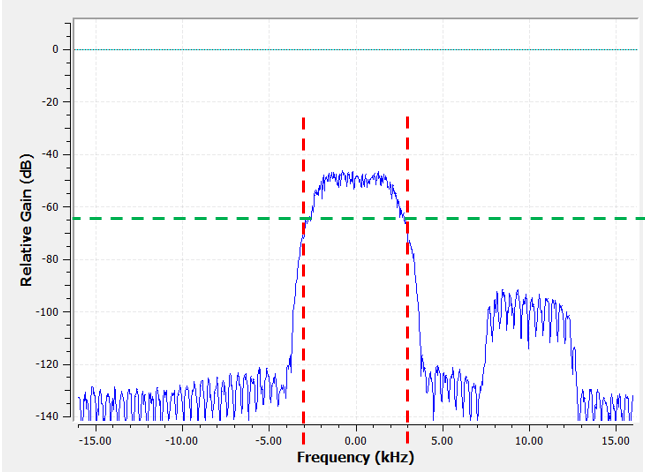
GNU Radio frequency domain plot of signal of interest and an interfering signal and noise floor, with interference filtered out

Esta señal filtrada parecerá confusa hasta que recuerdes que nuestro nivel de ruido estaba en la línea verde alrededor de -65 dB. Aunque todavía podemos ver la señal de interferencia centrada en 10 kHz, hemos disminuido severamente la potencia de esa señal. ¡Ahora está debajo de donde estaba el piso de ruido! También eliminamos la mayor parte del ruido que existía en la banda de parada.

Además de la frecuencia de corte, el otro parámetro principal de nuestro filtro de paso bajo se llama “ancho de transición”. El ancho de transición, también medido en Hz, indica al filtro qué tan rápido debe pasar entre la banda de paso y la banda de parada, ya que una transición instantánea es imposible.

Visualicemos el ancho de la transición. En el siguiente diagrama, la línea verde representa la respuesta ideal para la transición entre una banda de paso y una banda de parada, que esencialmente tiene un ancho de transición de cero. La línea Rojo muestra el resultado de un filtro realista, que tiene cierta ondulación y un cierto ancho de transición.

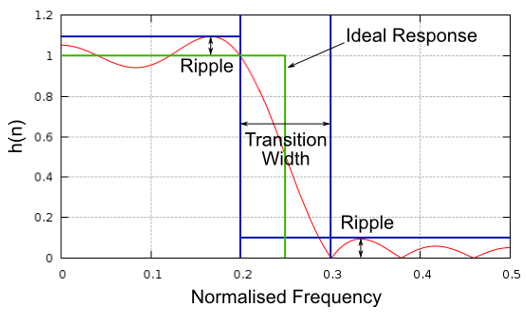
Frequency response of a low-pass filter, showing ripple and transition width

Quizás se pregunte por qué no establecemos el ancho de transición lo más pequeño posible. La razón es principalmente que un ancho de transición más pequeño da como resultado más taps, y más taps significa más cálculos; veremos por qué en breve. Un filtro de 50 taps puede funcionar durante todo el día utilizando el 1% de la CPU en una Raspberry Pi. Mientras tanto, ¡un filtro de 50.000 taps hará que tu CPU explote! Normalmente utilizamos una herramienta de diseño de filtros, luego vemos cuántas pulsaciones genera y, si son demasiadas (por ejemplo, más de 100), aumentamos el ancho de la transición. Por supuesto, todo depende de la aplicación y del hardware que ejecuta el filtro.

En el ejemplo de filtrado anterior, utilizamos un límite de 3 kHz y un ancho de transición de 1 kHz (es difícil ver el ancho de transición con solo mirar estas capturas de pantalla). El filtro resultante tenía 77 taps.

Volvamos a la representación del filtro. Aunque podemos mostrar la lista de taps para un filtro, normalmente representamos los filtros visualmente en el dominio de la frecuencia. A esto lo llamamos “respuesta de frecuencia” del filtro y nos muestra el comportamiento del filtro en frecuencia. Aquí está la respuesta de frecuencia del filtro que estábamos usando:

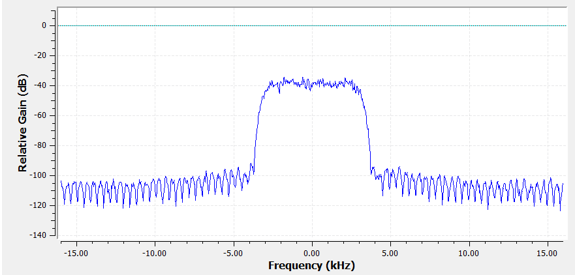
Tenga en cuenta que lo que estoy mostrando aquí no es una señal, es solo la representación del dominio de frecuencia del filtro. Esto puede ser un poco difícil de entender al principio, pero a medida que miramos los ejemplos y el código, encajará.

Un filtro determinado también tiene una representación en el dominio del tiempo; se llama “respuesta al impulso” del filtro porque es lo que ves en el dominio del tiempo si tomas un impulso y lo pasas por el filtro. (Google “Función delta de Dirac” para obtener más información sobre qué es un impulso). Para un filtro tipo FIR, la respuesta al impulso es simplemente los propios taps. Para ese filtro de 77 taps que usamos antes, los taps son:

h =  [-0.00025604525581002235, 0.00013669139298144728, 0.0005385575350373983,
0.0008378280326724052, 0.000906112720258534, 0.0006353431381285191,
-9.884083502996931e-19, -0.0008822851814329624, -0.0017323142383247614,
-0.0021665366366505623, -0.0018335371278226376, -0.0005912294145673513,
0.001349081052467227, 0.0033936649560928345, 0.004703888203948736,
0.004488115198910236, 0.0023609865456819534, -0.0013707970501855016,
-0.00564080523326993, -0.008859002031385899, -0.009428252466022968,
-0.006394983734935522, 4.76480351940553e-18, 0.008114570751786232,
0.015200719237327576, 0.018197273835539818, 0.01482443418353796,
0.004636279307305813, -0.010356673039495945, -0.025791890919208527,
-0.03587324544787407, -0.034922562539577484, -0.019146423786878586,
0.011919975280761719, 0.05478153005242348, 0.10243935883045197,
0.1458890736103058, 0.1762896478176117, 0.18720689415931702,
0.1762896478176117, 0.1458890736103058, 0.10243935883045197,
0.05478153005242348, 0.011919975280761719, -0.019146423786878586,
-0.034922562539577484, -0.03587324544787407, -0.025791890919208527,
-0.010356673039495945, 0.004636279307305813, 0.01482443418353796,
0.018197273835539818, 0.015200719237327576, 0.008114570751786232,
4.76480351940553e-18, -0.006394983734935522, -0.009428252466022968,
-0.008859002031385899, -0.00564080523326993, -0.0013707970501855016,
0.0023609865456819534, 0.004488115198910236, 0.004703888203948736,
0.0033936649560928345, 0.001349081052467227, -0.0005912294145673513,
-0.0018335371278226376, -0.0021665366366505623, -0.0017323142383247614,
-0.0008822851814329624, -9.884083502996931e-19, 0.0006353431381285191,
0.000906112720258534, 0.0008378280326724052, 0.0005385575350373983,
0.00013669139298144728, -0.00025604525581002235]

Y aunque todavía no hemos entrado en el diseño del filtro, aquí está el código Python que generó ese filtro:

import numpy as np
from scipy import signal
import matplotlib.pyplot as plt

num_taps = 51 # it helps to use an odd number of taps
cut_off = 3000 # Hz
sample_rate = 32000 # Hz

# create our low pass filter
h = signal.firwin(num_taps, cut_off, fs=sample_rate)

# plot the impulse response
plt.plot(h, '.-')
plt.show()

Simplemente trazar esta serie de floats nos da la respuesta al impulso del filtro:

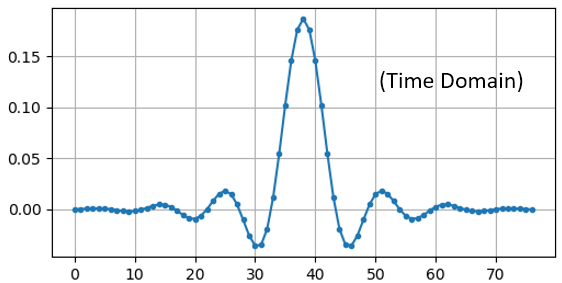
Example of impulse response of a filter, plotting the taps in the time domain

Y aquí está el código que se usó para producir la respuesta de frecuencia, mostrado anteriormente. Es un poco más complicado porque tenemos que crear el conjunto de frecuencias del eje x.

# plot the frequency response
H = np.abs(np.fft.fft(h, 1024)) # take the 1024-point FFT and magnitude
H = np.fft.fftshift(H) # make 0 Hz in the center
w = np.linspace(-sample_rate/2, sample_rate/2, len(H)) # x axis
plt.plot(w, H, '.-')
plt.show()

Filtros Reales vs. Complejos¶

El filtro que les mostré tenía taps reales, pero los taps también pueden ser complejos. Si los taps son reales o complejas, no tiene por qué coincidir con la señal de entrada, es decir, puede pasar una señal compleja a través de un filtro con taps reales y viceversa. Cuando los taps son reales, la respuesta de frecuencia del filtro será simétrica alrededor de DC (0 Hz). Normalmente utilizamos taps complejos cuando necesitamos asimetría, lo que no ocurre con demasiada frecuencia.

Figure made with TikZ

Como ejemplo de taps complejas, volvamos al caso de uso del filtrado, excepto que esta vez queremos recibir la otra señal de interferencia (sin tener que volver a sintonizar la radio). Eso significa que queremos un filtro de paso de banda, pero no simétrico. Solo queremos mantener (también conocidas como “pass”) frecuencias entre 7 kHz y 13 kHz (no queremos pasar también de -13 kHz a -7 kHz)

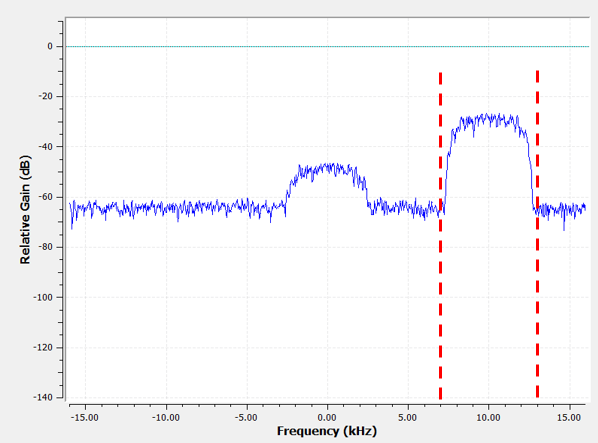
Una forma de diseñar este tipo de filtro es crear un filtro paso bajo con un corte de 3 kHz y luego cambiarlo de frecuencia. Recuerde que podemos desplazar la frecuencia x(t) (dominio del tiempo) multiplicándola por $e^{j2\pi f_0t}$ . En este caso $f_0$ debería ser 10 kHz, lo que eleva nuestro filtro 10 kHz. Recuerde que en nuestro código Python de arriba, $h$ eran los taps del filtro del filtro paso bajo. Para crear nuestro filtro paso banda solo tenemos que multiplicar esos taps por $e^{j2\pi f_0t}$ , aunque implicaría crear un vector para representar el tiempo en función de nuestro período de muestreo (inverso de la frecuencia de muestreo):

# (h was found using the first code snippet)

# Shift the filter in frequency by multiplying by exp(j*2*pi*f0*t)
f0 = 10e3 # amount we will shift
Ts = 1.0/sample_rate # sample period
t = np.arange(0.0, Ts*len(h), Ts) # time vector. args are (start, stop, step)
exponential = np.exp(2j*np.pi*f0*t) # this is essentially a complex sine wave

h_band_pass = h * exponential # do the shift

# plot impulse response
plt.figure('impulse')
plt.plot(np.real(h_band_pass), '.-')
plt.plot(np.imag(h_band_pass), '.-')
plt.legend(['real', 'imag'], loc=1)

# plot the frequency response
H = np.abs(np.fft.fft(h_band_pass, 1024)) # take the 1024-point FFT and magnitude
H = np.fft.fftshift(H) # make 0 Hz in the center
w = np.linspace(-sample_rate/2, sample_rate/2, len(H)) # x axis
plt.figure('freq')
plt.plot(w, H, '.-')
plt.xlabel('Frequency [Hz]')
plt.show()

Los gráficos de la respuesta al impulso y la respuesta en frecuencia se muestran a continuación:

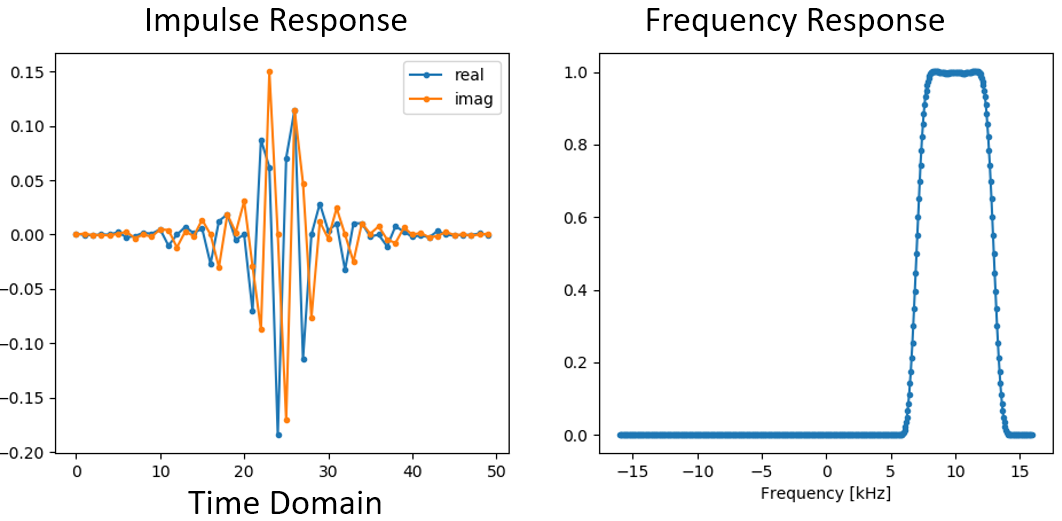
Debido a que nuestro filtro no es simétrico alrededor de 0 Hz, tiene que utilizar taps complejos. Por lo tanto, necesitamos dos líneas para trazar esos taps complejos. Lo que vemos en el gráfico de la izquierda de arriba sigue siendo la respuesta al impulso. Nuestro gráfico de respuesta de frecuencia es lo que realmente valida que creamos el tipo de filtro que esperábamos, donde filtrará todo excepto la señal centrada alrededor de 10 kHz. Una vez más, recuerde que el gráfico anterior no es una señal real: es solo una representación del filtro. Puede ser muy confuso de entender porque cuando aplicas el filtro a la señal y trazas la salida en el dominio de la frecuencia, en muchos casos se verá más o menos igual que la respuesta de frecuencia del filtro.

Si esta subsección aumentó la confusión, no se preocupe, el 99% de las veces tendrá que lidiar con filtros paso bajo simples con taps reales de todos modos.

Implementación de Filtros¶

No vamos a profundizar demasiado en la implementación de filtros. Más bien, me concentro en el diseño de filtros (de todos modos, puede encontrar implementaciones listas para usar en cualquier lenguaje de programación). Por ahora, aquí hay una conclusión: para filtrar una señal con un filtro FIR, simplemente convoluciona la respuesta al impulso (el conjunto de taps) con la señal de entrada. (No se preocupe, una sección posterior explica la convolución). En el mundo discreto usamos una convolución discreta (ejemplo a continuación). Los triángulos etiquetados como b son los taps. En el diagrama de flujo, los cuadrados etiquetados $z^{-1}$ encima de los triángulos significan un retraso de un paso de tiempo.

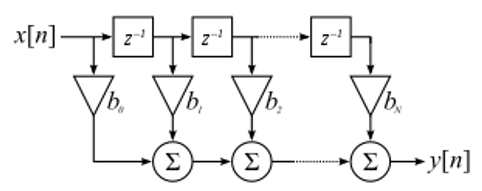
Implementation of a finite impulse response (FIR) filter with delays and taps and summations

Es posible que pueda ver por qué ahora los llamamos “taps” del filtro, según la forma en que se implementa el filtro.

FIR vs IIR¶

Hay dos clases principales de filtros digitales: FIR y IIR.

Finite impulse response (FIR)
Infinite impulse response (IIR)

No profundizaremos demasiado en la teoría, pero por ahora recuerde: los filtros FIR son más fáciles de diseñar y pueden hacer lo que quiera si usa suficientes taps. Los filtros IIR son más complicados y pueden ser inestables, pero son más eficientes (utilizan menos CPU y memoria para el filtro determinado). Si alguien simplemente le da una lista de taps, se supone que son taps para un filtro FIR. Si empiezan a hablar de “polos”, están hablando de filtros IIR. Nos quedaremos con los filtros FIR en este libro de texto.

A continuación se muestra un ejemplo de respuesta de frecuencia, comparando un filtro FIR e IIR que realizan casi exactamente el mismo filtrado; tienen un ancho de transición similar, que, como aprendimos, determinará cuántos taps se requieren. El filtro FIR tiene 50 taps y el filtro IIR tiene 12 polos, lo que es como tener 12 taps en términos de cálculos necesarios.

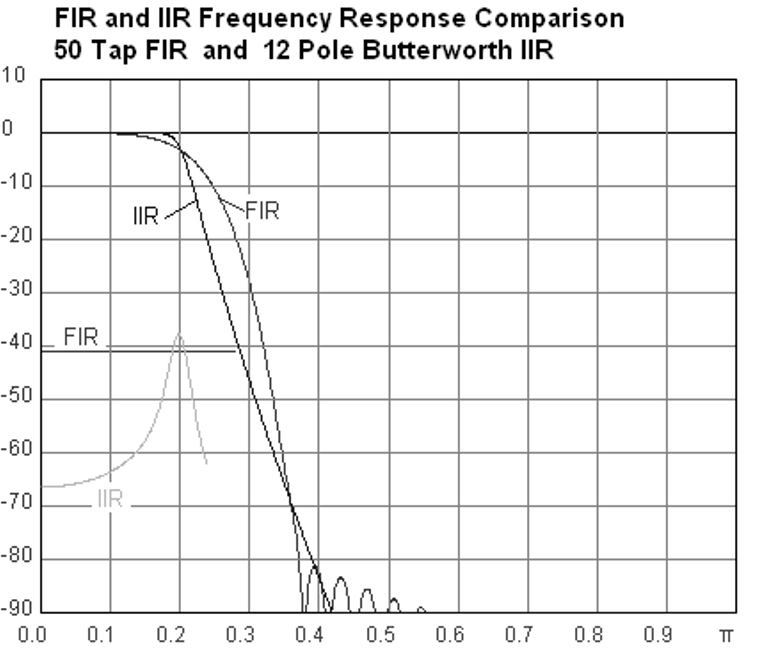
Comparing finite impulse response (FIR) and infinite impulse response (IIR) filters by observing frequency response

La lección es que el filtro FIR requiere muchos más recursos computacionales que el IIR para realizar aproximadamente la misma operación de filtrado.

A continuación se muestran algunos ejemplos del mundo real de filtros FIR e IIR que quizás haya utilizado antes.

Si realiza una “media móvil” en una lista de números, eso es solo un filtro FIR con taps de unos: - h = [1 1 1 1 1 1 1 1 1 1] para un filtro de media móvil con un tamaño de ventana de 10. También resulta ser un filtro de tipo paso bajo; ¿porqué es eso? ¿Cuál es la diferencia entre usar 1 y usar grifos que decaen a cero?

Answers

Un filtro de media móvil es un filtro paso bajo porque suaviza los cambios de “alta frecuencia”, razón por la cual la gente lo suele utilizar. La razón para usar taps que decaen a cero en ambos extremos es para evitar un cambio repentino en la salida, como si la señal que se filtra fuera cero por un tiempo y luego de repente saltara.

Ahora veamos un ejemplo de IIR. ¿Alguno de ustedes ha hecho esto alguna vez?

x = x*0.99 + new_value*0.01

donde 0,99 y 0,01 representan la velocidad con la que se actualiza el valor (o la tasa de caída, lo mismo). Es una forma conveniente de actualizar lentamente alguna variable sin tener que recordar los últimos valores. En realidad, se trata de una forma de filtro IIR de paso bajo. Con suerte, podrá ver por qué los filtros IIR tienen menos estabilidad que los FIR. ¡Los valores nunca desaparecen por completo!

Herramientas de diseño de filtros¶

En la práctica, la mayoría de la gente utilizará una herramienta de diseño de filtros o una función en el código que diseñe el filtro. Hay muchas herramientas diferentes, pero a los estudiantes les recomiendo esta aplicación web fácil de usar de Peter Isza que les mostrará la respuesta de impulso y frecuencia: http://t-filter.engineerjs.com. Usando los valores predeterminados, al menos al momento de escribir esto, está configurado para diseñar un filtro paso bajo con una banda de paso de 0 a 400 Hz y una banda de parada de 500 Hz en adelante. La frecuencia de muestreo es de 2 kHz, por lo que la frecuencia máxima que podemos “ver” es 1 kHz.

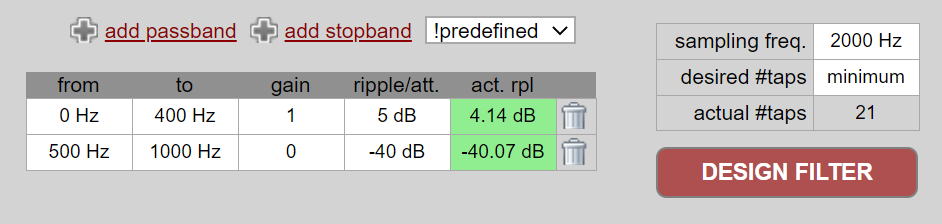
Haga clic en el botón “Filtro de diseño” para crear los taps y trazar la respuesta de frecuencia.

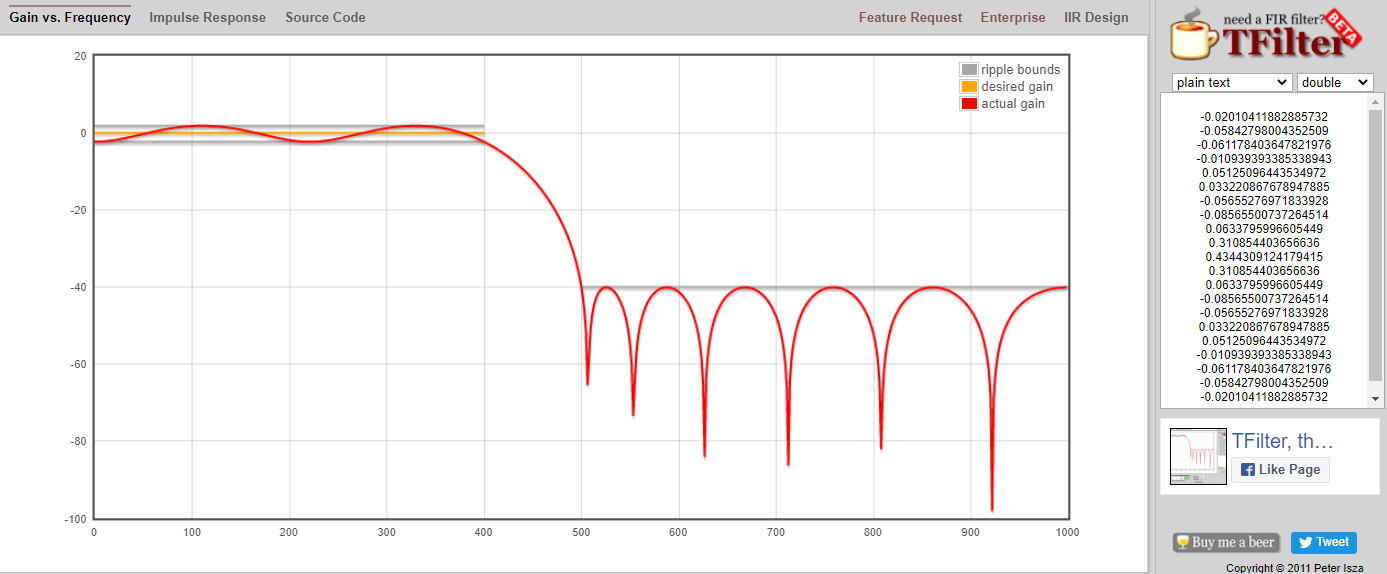
Haga clic en el texto “Respuesta al impulso” encima del gráfico para ver la respuesta al impulso, que es un gráfico de los taps, ya que se trata de un filtro FIR.

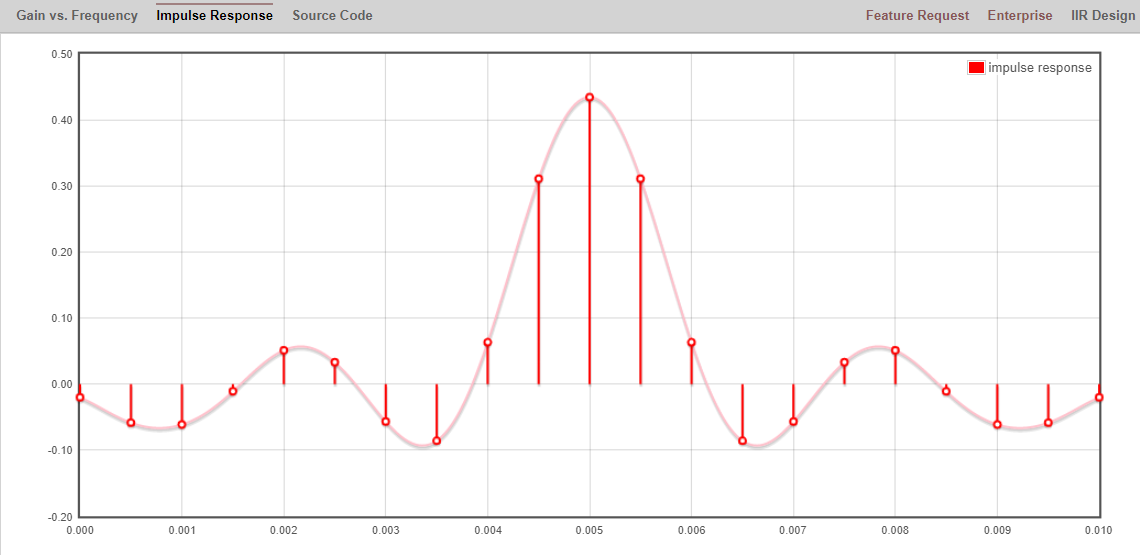
Esta aplicación incluso incluye el código fuente C++ para implementar y utilizar este filtro. La aplicación web no incluye ninguna forma de diseñar filtros IIR, que en general son mucho más difíciles de diseñar.

Convolución¶

Nos desviaremos brevemente para presentar el operador de convolución. No dudes en saltarte esta sección si ya estás familiarizado con ella.

Sumar dos señales es una forma de combinar dos señales en una. En el capitulo Dominio de la Frecuencia exploramos cómo se aplica la propiedad de linealidad al sumar dos señales. La convolución es otra forma de combinar dos señales en una, pero es muy diferente a simplemente sumarlas. La convolución de dos señales es como deslizar una sobre la otra e integrarla. Es muy similar a una correlación cruzada, si está familiarizado con esa operación. De hecho, en muchos casos equivale a una correlación cruzada. Normalmente utilizamos el símbolo ::code::* para referirse a una convolución, especialmente en ecuaciones matemáticas.

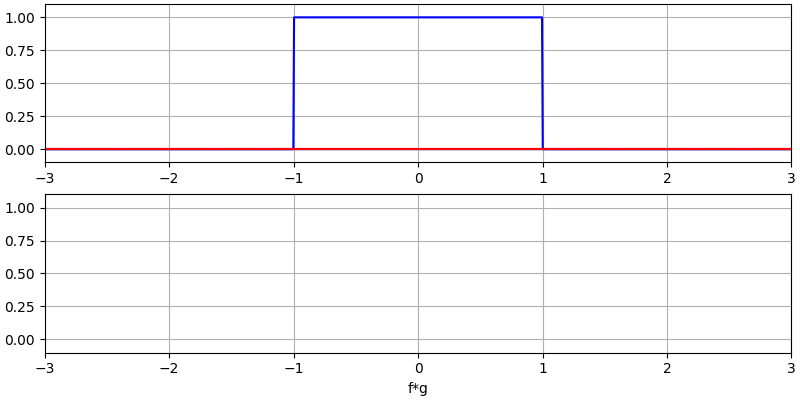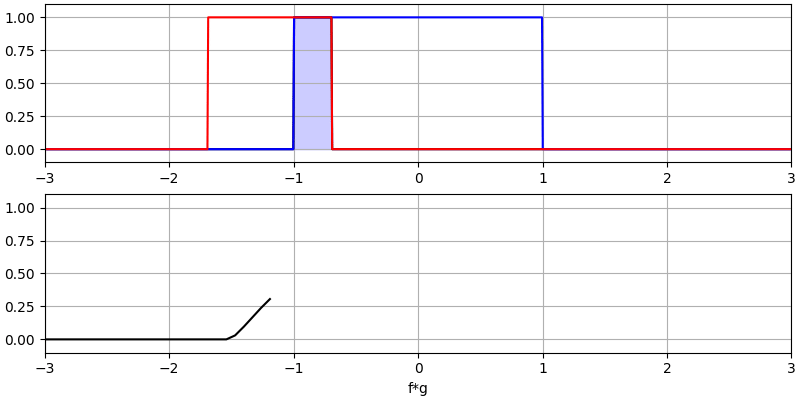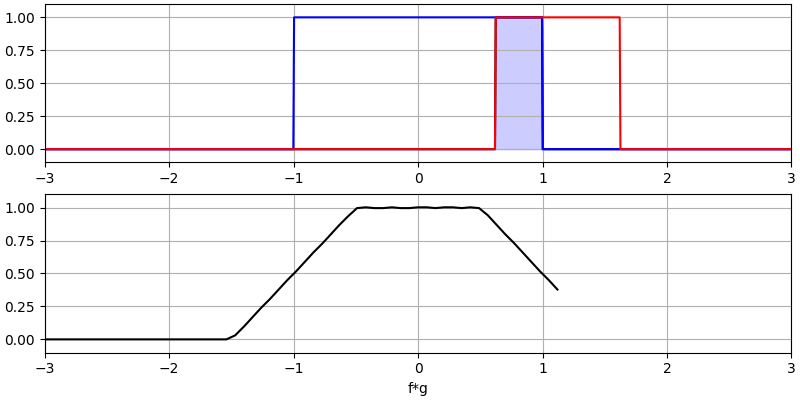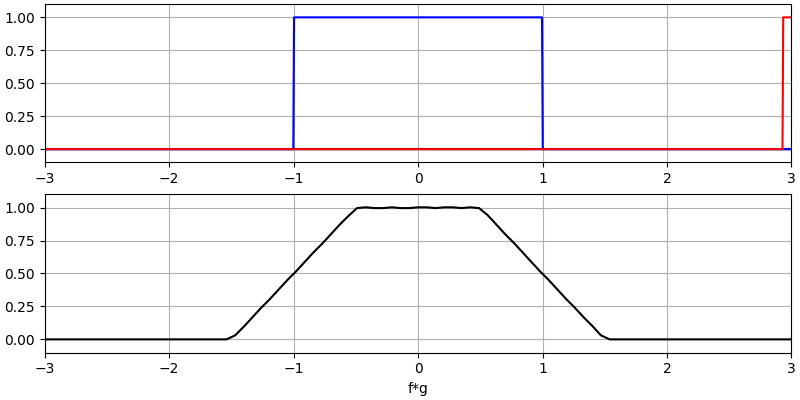
Creo que la operación de convolución se aprende mejor a través de ejemplos. En este primer ejemplo, convolucionamos dos pulsos cuadrados juntos:

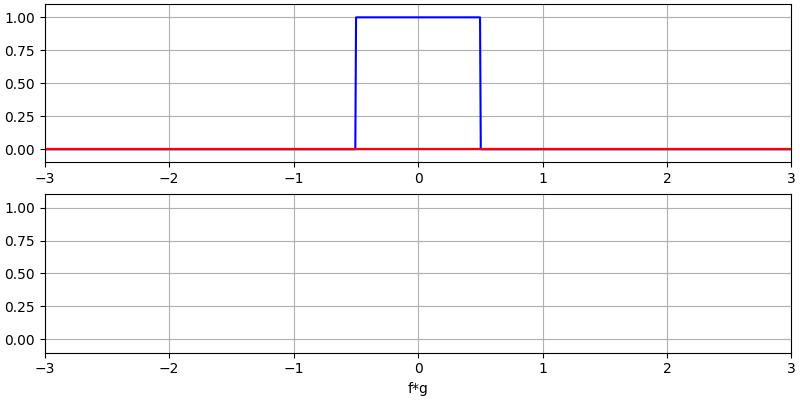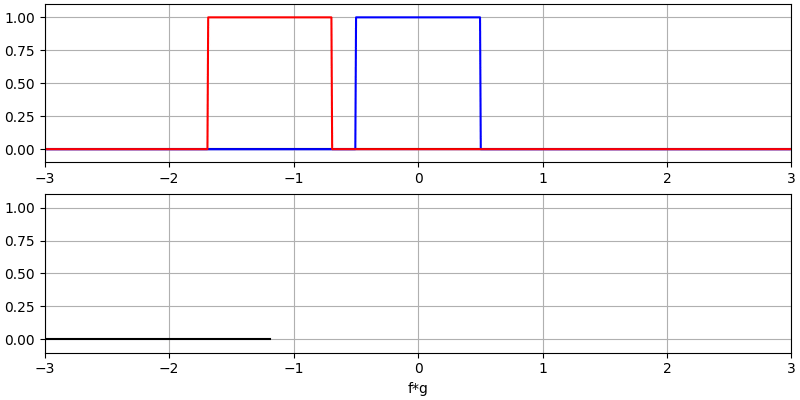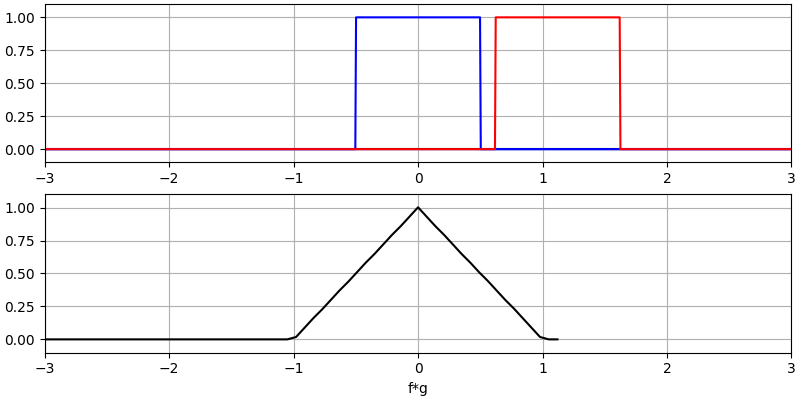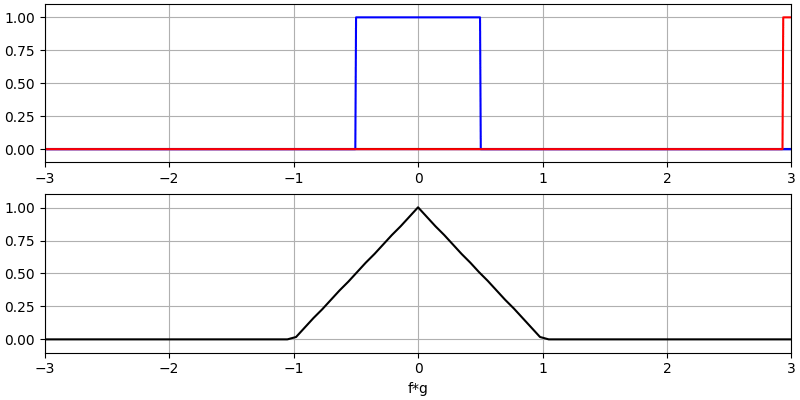
Tenemos dos señales de entrada (una roja y otra azul) y luego la salida de la convolución se muestra en negro. Puede ver que la salida es la integración de las dos señales cuando una se desliza sobre la otra. Debido a que es solo una integración deslizante, el resultado es un triángulo con un máximo en el punto donde ambos pulsos cuadrados se alinearon perfectamente.

Veamos algunas convoluciones más:

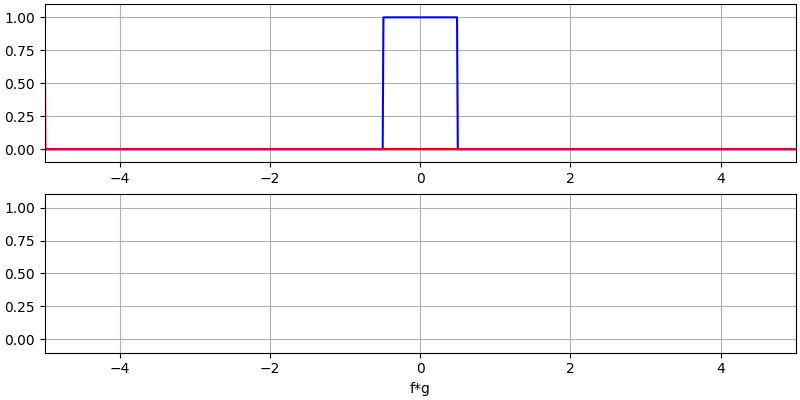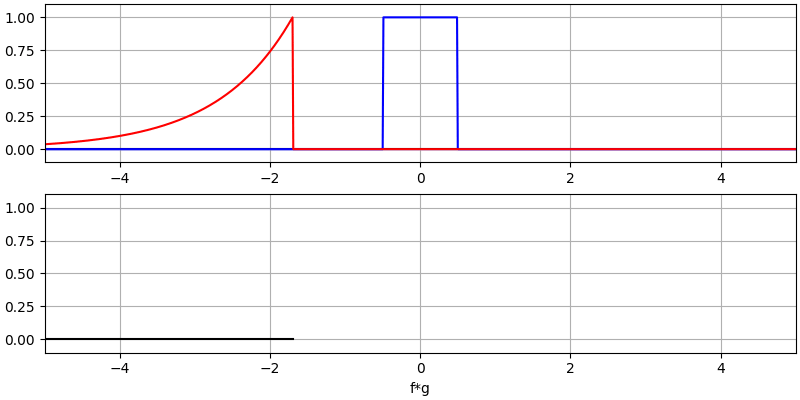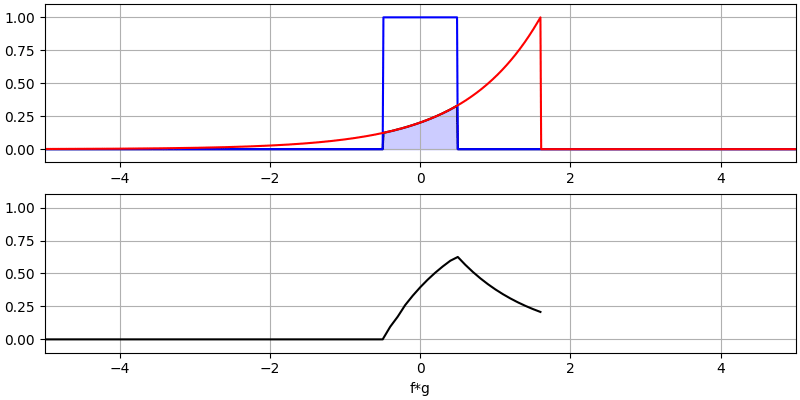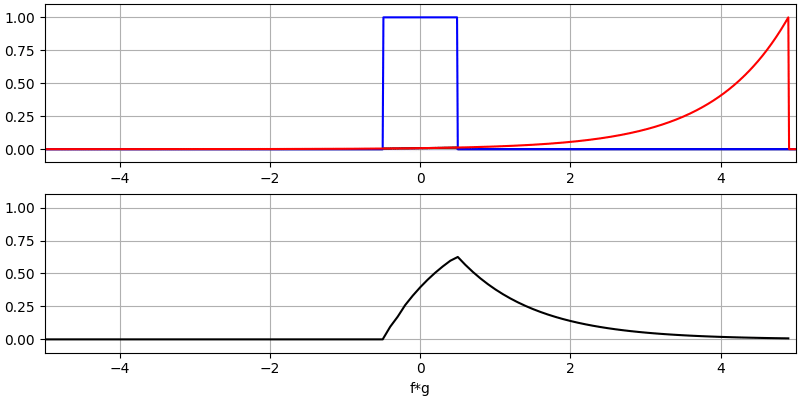
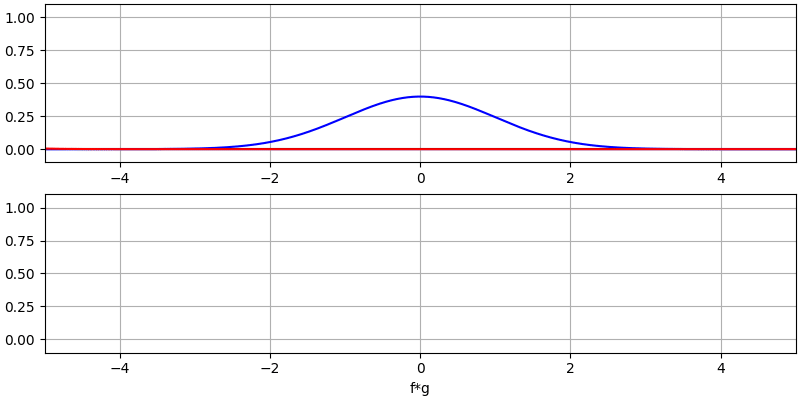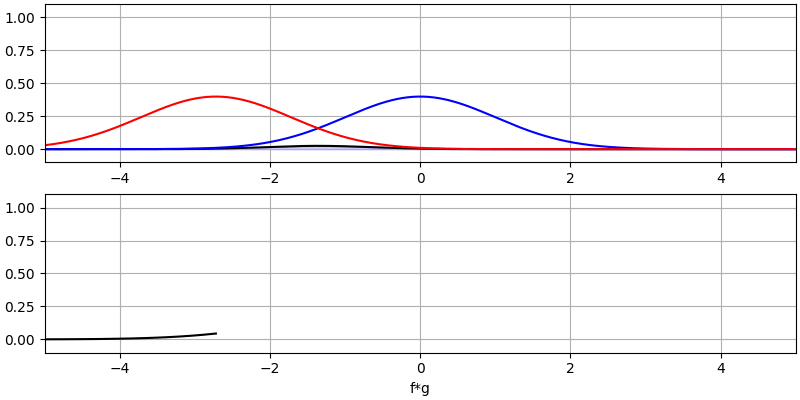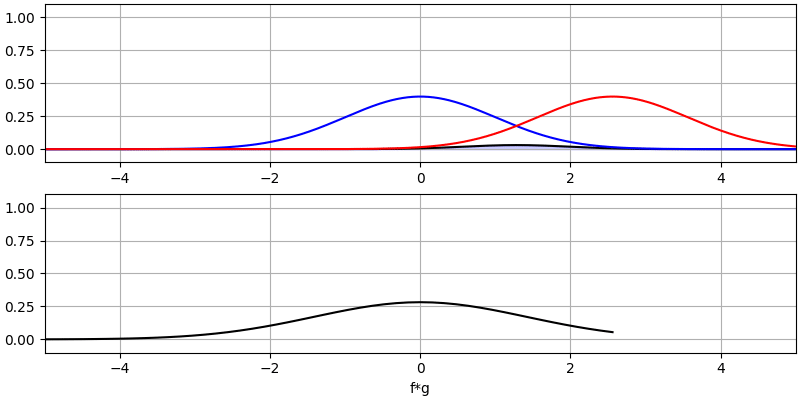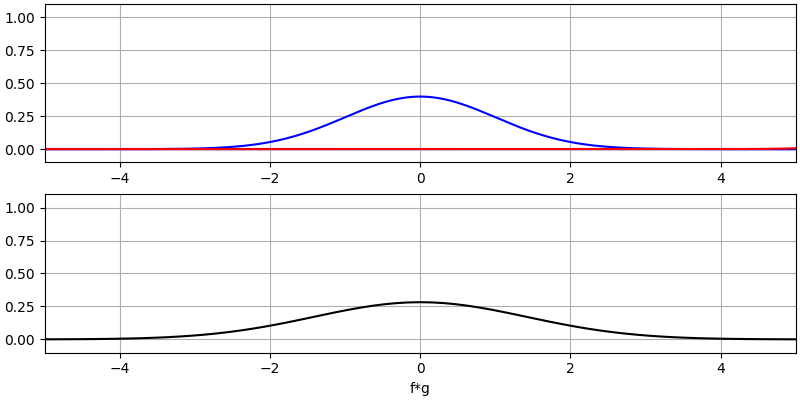
Observe cómo una gaussiana convolucionada con otra gaussiana es otra gaussiana, pero con un pulso más amplio y una amplitud menor.

Debido a esta naturaleza “deslizante”, la longitud de la salida es en realidad más larga que la de la entrada. Si una señal tiene M muestras y la otra señal es N muestras, La convolución de los dos puede producir N+M-1 muestras. Sin embargo, funciones como numpy.convolve() tiene una manera de especificar si desea la salida completa (max(M, N) muestras) o simplemente las muestras donde las señales se superpusieron completamente (max(M, N) - min(M, N) + 1 si eres curioso). No hay necesidad de quedar atrapado en este detalle. Solo sepa que la longitud de la salida de una convolución no es solo la longitud de las entradas.

Entonces, ¿por qué es importante la convolución en DSP? Bueno, para empezar, para filtrar una señal, simplemente podemos tomar la respuesta al impulso de ese filtro y convolucionarla con la señal. El filtrado FIR es simplemente una operación de convolución.

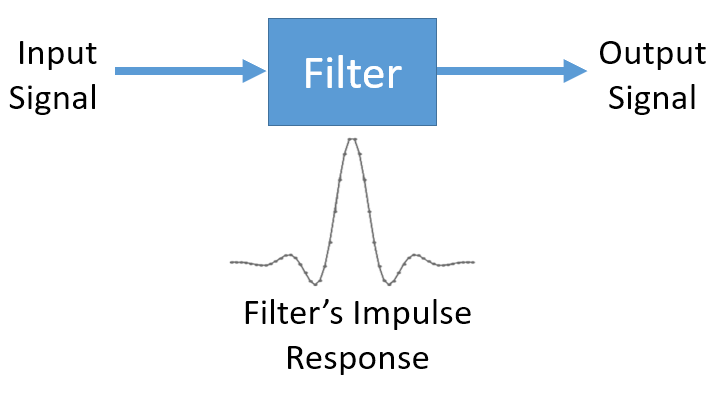
Puede resultar confuso porque antes mencionamos que la convolución recibe dos señales y genera una. Podemos tratar la respuesta al impulso como una señal y, después de todo, la convolución es un operador matemático que opera en dos matrices 1D. Si una de esas matrices 1D es la respuesta de impulso del filtro, la otra matriz 1D puede ser una parte de la señal de entrada y la salida será una versión filtrada de la entrada.

Veamos otro ejemplo para ayudar a este clic. En el siguiente ejemplo, el triángulo representará la respuesta al impulso de nuestro filtro, y la señal en verde es nuestra señal que está siendo filtrada.

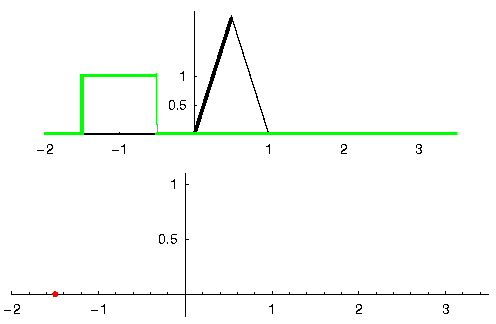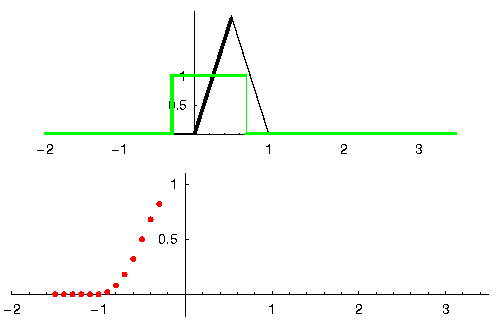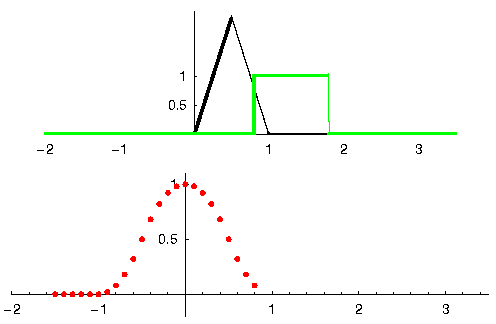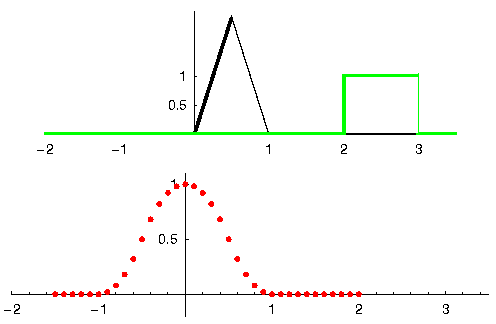
La salida en rojo es la señal filtrada.

Pregunta: ¿Qué tipo de filtro era el triángulo?

Answers

Suavizó los componentes de alta frecuencia de la señal verde (es decir, las transiciones bruscas del cuadrado) para que actúe como un filtro de paso bajo.

Ahora que estamos empezando a comprender la convolución, presentaré la ecuación matemática. El asterisco (*) se utiliza normalmente como símbolo de convolución:

$(f * g)(t) = \int f(\tau) g(t - \tau) d\tau$

En la siguiente expresión, $g(t)$ es la señal o la entrada que se refleja sobre y y se desliza a lo largo de x $f(t)$ , pero $g(t)$ y $f(t)$ se puede intercambiar y sigue siendo la misma expresión. Normalmente, la matriz más corta se utilizará como $g(t)$ . La convolución es igual a una correlación cruzada, definida como $\int f(\tau) g(t+\tau)$ , cuando $g(t)$ es simétrica, es decir, no cambia cuando se le da la vuelta sobre el origen.

Diseño de filtros en Python¶

Ahora consideraremos una forma de diseñar nosotros mismos un filtro FIR en Python. Si bien existen muchos enfoques para diseñar filtros, usaremos el método de comenzar en el dominio de la frecuencia y trabajar hacia atrás para encontrar la respuesta al impulso. En última instancia, así es como se representa nuestro filtro (por sus taps).

Empiece por crear un vector de la respuesta de frecuencia deseada. Diseñemos un filtro de paso bajo de forma arbitraria que se muestra a continuación:

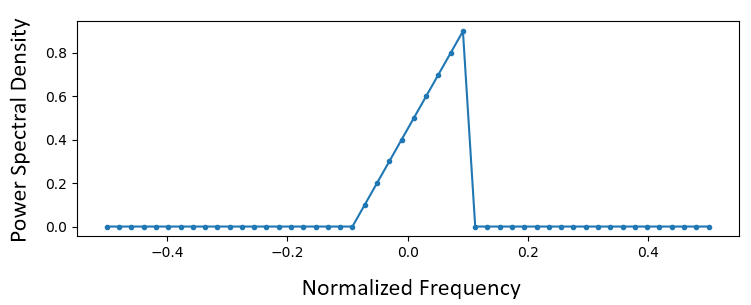
El código utilizado para crear este filtro es bastante simple:

import numpy as np
import matplotlib.pyplot as plt
H = np.hstack((np.zeros(20), np.arange(10)/10, np.zeros(20)))
w = np.linspace(-0.5, 0.5, 50)
plt.plot(w, H, '.-')
plt.show()

hstack() es una forma de concatenar matrices en numpy. Sabemos que conducirá a un filtro con taps complejos. ¿Por qué?

Answer

No es simétrico alrededor de 0 Hz.

Nuestro objetivo final es encontrar los taps de este filtro para que podamos usarlo. ¿Cómo obtenemos los taps, dada la respuesta de frecuencia? Bueno, ¿cómo convertimos del dominio de la frecuencia al dominio del tiempo? ¡FFT inversa (IFFT)! Recuerde que la función IFFT es casi exactamente igual que la función FFT. También necesitamos cambiar IFFT nuestra respuesta de frecuencia deseada antes de IFFT, y luego necesitamos otro cambio IFF después de IFFT (no, no se cancelan solos, puedes intentarlo). Este proceso puede parecer confuso. Sólo recuerda que siempre debes tener la FFTshift después de una FFT y IFFshift después de una IFFT.

h = np.fft.ifftshift(np.fft.ifft(np.fft.ifftshift(H)))
plt.plot(np.real(h))
plt.plot(np.imag(h))
plt.legend(['real','imag'], loc=1)
plt.show()

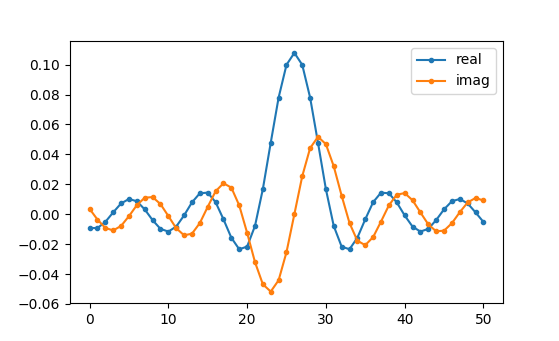
Usaremos estos taps que se muestran arriba como nuestro filtro. Sabemos que la respuesta al impulso está trazando los taps, por lo que lo que vemos arriba es nuestra respuesta al impulso. Tomemos la FFT de nuestros taps para ver cómo se ve realmente el dominio de la frecuencia. Haremos una FFT de 1.024 puntos para conseguir una alta resolución:

H_fft = np.fft.fftshift(np.abs(np.fft.fft(h, 1024)))
plt.plot(H_fft)
plt.show()

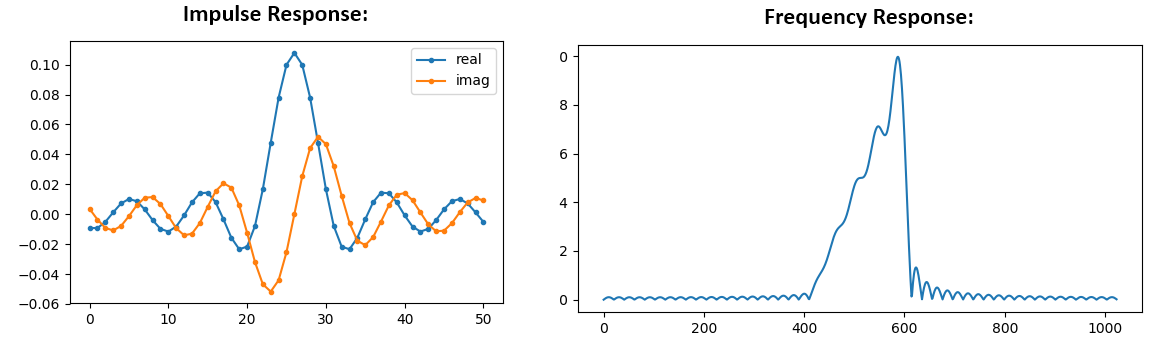
Vea cómo la respuesta de frecuencia no es muy recta… no coincide muy bien con nuestro original, si recuerda la forma para la que inicialmente queríamos hacer un filtro. Una razón importante es que nuestra respuesta al impulso no ha terminado de decaer, es decir, los lados izquierdo y derecho no llegan a cero. Tenemos dos opciones que le permitirán decaer a cero:

Opción 1: Creamos una ventana en nuestra respuesta de impulso actual para que descienda a 0 en ambos lados. Implica multiplicar nuestra respuesta al impulso con una “función de ventana” que comienza y termina en cero.

# After creating h using the previous code, create and apply the window
window = np.hamming(len(h))
h = h * window

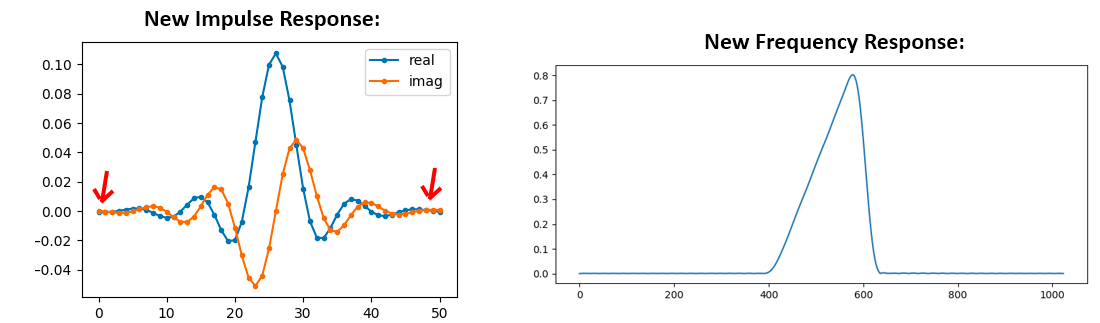
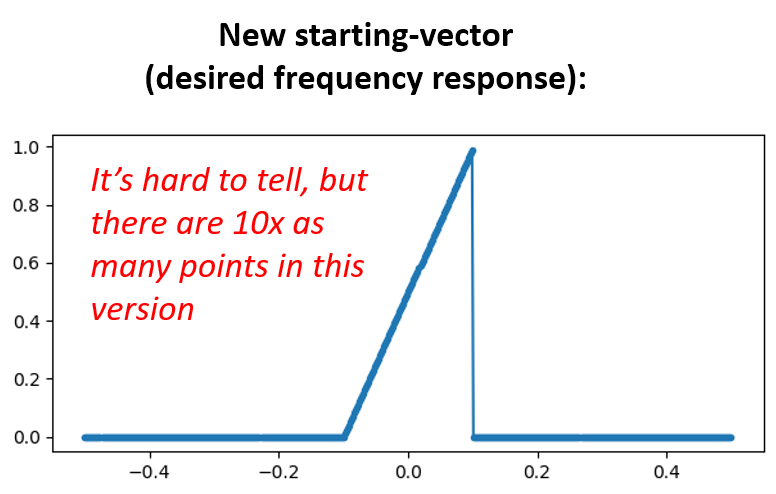
Opción 2: Regeneramos nuestra respuesta impulso usando más puntos para que tenga tiempo de decaer. Necesitamos agregar resolución a nuestra matriz de dominio de frecuencia original (lo que se llama interpolación).

H = np.hstack((np.zeros(200), np.arange(100)/100, np.zeros(200)))
w = np.linspace(-0.5, 0.5, 500)
plt.plot(w, H, '.-')
plt.show()
# (the rest of the code is the same)

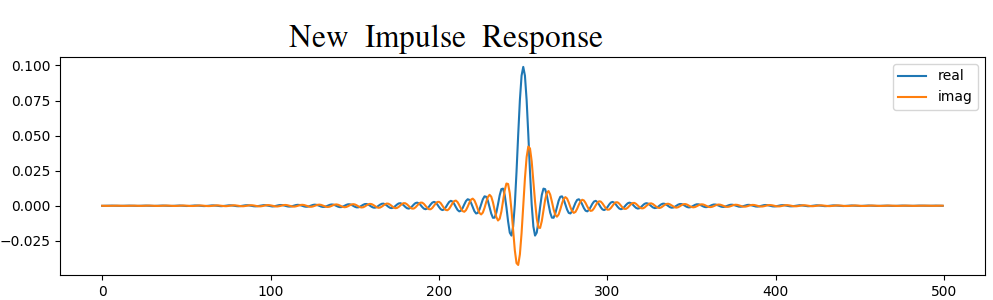
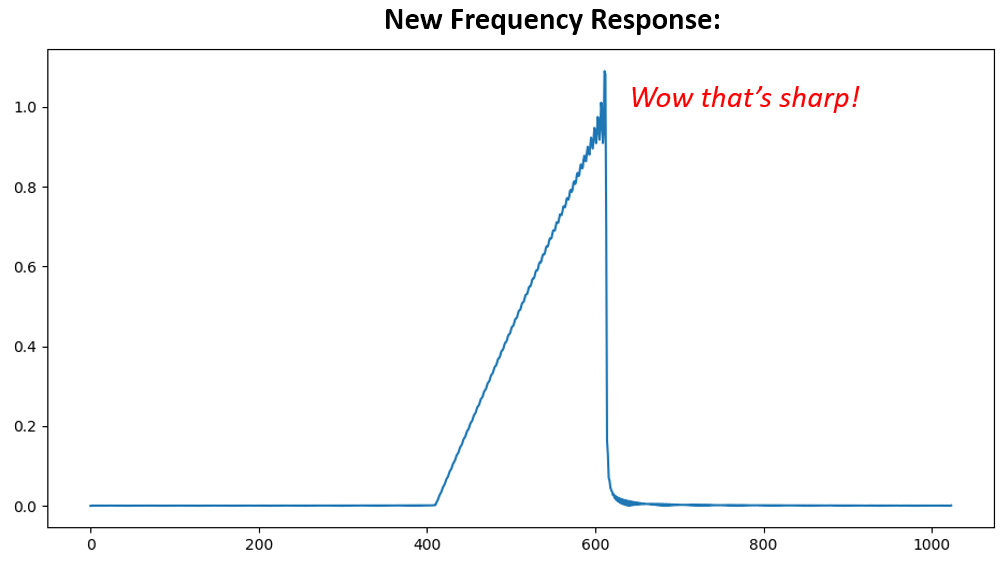
Ambas opciones funcionaron. ¿Cuál elegirías? El segundo método resultó en más pulsaciones, pero el primer método resultó en una respuesta de frecuencia que no era muy nítida y tenía un flanco descendente que no era muy pronunciado. Existen numerosas formas de diseñar un filtro, cada una con sus propias compensaciones a lo largo del camino. Muchos consideran que el diseño de filtros es un arte.

Introducción al formador de pulsos¶

Introduciremos brevemente un tema muy interesante dentro del DSP, el modelado de pulsos. Consideraremos el tema en profundidad en su propio capítulo más adelante, ver Formador de Pulso. Vale la pena mencionarlo junto con el filtrado porque la conformación de pulsos es, en última instancia, un tipo de filtro, utilizado para un propósito específico, con propiedades especiales.

Como aprendimos, las señales digitales utilizan símbolos para representar uno o más bits de información. Utilizamos un esquema de modulación digital como ASK, PSK, QAM, FSK, etc., para modular una portadora de modo que la información pueda enviarse de forma inalámbrica. Cuando simulamos QPSK en el capítulo Modulación Digital, solo simulamos una muestra por símbolo, es decir, cada número complejo que creamos era uno de los puntos de la constelación: era un símbolo. En la práctica, normalmente generamos varias muestras por símbolo y el motivo tiene que ver con el filtrado.

Usamos filtros para crear la “forma” de nuestros símbolos porque la forma en el dominio del tiempo cambia la forma en el dominio de la frecuencia. El dominio de la frecuencia nos informa cuánto espectro/ancho de banda utilizará nuestra señal y, por lo general, queremos minimizarlo. Lo que es importante entender es que las características espectrales (dominio de frecuencia) de los símbolos de banda base no cambian cuando modulamos una portadora; simplemente aumenta la frecuencia de la banda base mientras la forma permanece igual, lo que significa que la cantidad de ancho de banda que utiliza permanece igual. Cuando usamos 1 muestra por símbolo, es como transmitir pulsos cuadrados. De hecho, BPSK que usa 1 muestra por símbolo es solo una onda cuadrada de 1’s y -1’s aleatorios:

Y como hemos aprendido, los pulsos cuadrados no son eficientes porque utilizan una cantidad excesiva de espectro:

Entonces, lo que hacemos es “dar forma a pulsos” a estos símbolos que parecen bloques para que ocupen menos ancho de banda en el dominio de la frecuencia. La “forma del pulso” se logra mediante el uso de un filtro de paso bajo porque descarta los componentes de frecuencia más alta de nuestros símbolos. A continuación se muestra un ejemplo de símbolos en el dominio del tiempo (arriba) y de la frecuencia (abajo), antes y después de que se haya aplicado un filtro de conformación de pulsos:

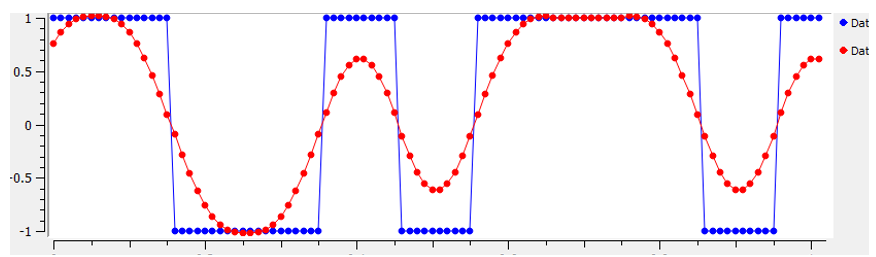
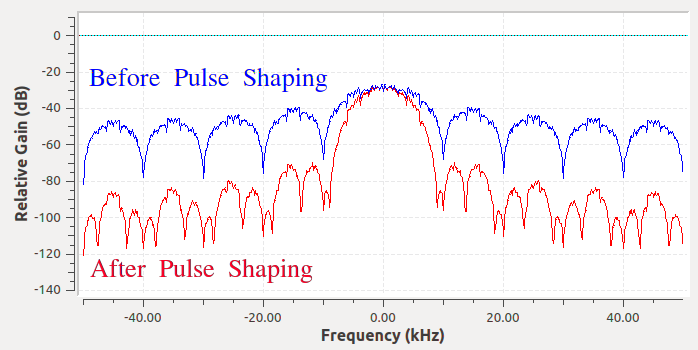
Demonstration of pulse shaping of an RF signal to reduce occupied bandwidth

Observe cuánto más rápido cae la frecuencia de la señal. Los lóbulos laterales son ~30 dB más bajos después de la configuración del pulso; ¡Eso es 1000 veces menos! Y lo que es más importante, el lóbulo principal es más estrecho, por lo que se utiliza menos espectro para la misma cantidad de bits por segundo.

Por ahora, tenga en cuenta que los filtros de formación de pulso más comunes incluyen:

Raised-cosine filter
Root raised-cosine filter
Sinc filter
Gaussian filter

Estos filtros generalmente tienen un parámetro que puede ajustar para disminuir el ancho de banda utilizado. A continuación se muestra el dominio de tiempo y frecuencia de un filtro de coseno elevado con diferentes valores de $\beta$ , el parámetro que define qué tan pronunciada es la caída.

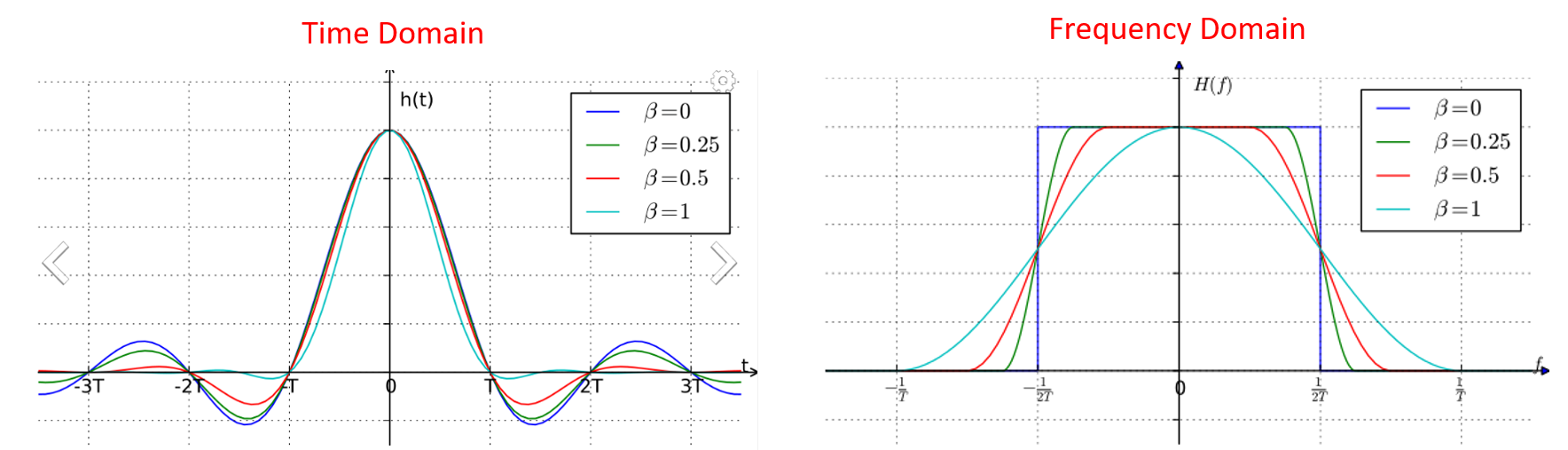
Puede ver que un valor más bajo de $\beta$ reduce el espectro utilizado (para la misma cantidad de datos). Sin embargo, si el valor es demasiado bajo, los símbolos en el dominio del tiempo tardarán más en decaer hasta cero. En realidad, cuando $\beta=0$ los símbolos nunca decaen completamente a cero, lo que significa que no podemos transmitir dichos símbolos en la práctica. Un valor $\beta$ de alrededor de 0,35 es común.

Aprenderá mucho más sobre la formación de pulsos, incluidas algunas propiedades especiales que deben satisfacer los filtros formadores de pulsos, en el capitulo Formador de Pulso .