3. Muestreo IQ¶

En este capítulo presentamos un concepto llamado muestreo IQ, también conocido como muestreo complejo o muestreo en cuadratura. También cubrimos muestreo de Nyquist, números complejos, portadoras de RF, conversión descendente y densidad espectral de potencia. El muestreo IQ es la forma de muestreo que realiza un SDR, así como muchos receptores (y transmisores) digitales. Es una versión un poco más compleja del muestreo digital normal (juego de palabras), así que lo tomaremos con calma y con un poco de práctica, ¡el concepto seguramente encajará!

Muestreo Basico¶

Antes de pasar al muestreo de IQ, analicemos qué significa realmente el muestreo. Es posible que te hayas encontrado con el muestreo sin darte cuenta al grabar audio con un micrófono. El micrófono es un transductor que convierte ondas sonoras en una señal eléctrica (un nivel de voltaje). Esa señal eléctrica es transformada por un convertidor analógico a digital (ADC), produciendo una representación digital de la onda sonora. Para simplificar, el micrófono captura ondas sonoras que se convierten en electricidad, y esa electricidad a su vez se convierte en números. El ADC actúa como puente entre los dominios analógico y digital. Los SDR son sorprendentemente similares. Sin embargo, en lugar de un micrófono utilizan una antena, aunque también utilizan ADC. En ambos casos, el nivel de voltaje se muestrea con un ADC. Para los SDR, piense en las ondas de radio y luego en los números.

Ya sea que estemos tratando con frecuencias de audio o radio, debemos muestrear si queremos capturar, procesar o guardar una señal digitalmente. El muestreo puede parecer sencillo, pero implica mucho. Una forma más técnica de pensar en el muestreo de una señal es tomar valores en momentos determinados y guardarlos digitalmente. Digamos que tenemos alguna función aleatoria, $S(t)$ , que podría representar cualquier cosa, y es una función continua que queremos muestrear:

Concept of sampling a signal, showing sample period T, the samples are the blue dots

Registramos el valor de $S(t)$ a intervalos regulares de $T$ segundos, conocido como período de muestreo. La frecuencia con la que tomamos muestras, es decir, el número de muestras tomadas por segundo, es simplemente $\frac{1}{T}$ . A esto lo llamamos tasa de muestreo y es la inversa del período de muestreo. Por ejemplo, si tenemos una frecuencia de muestreo de 10 Hz, entonces el período de muestreo es de 0,1 segundos; habrá 0,1 segundos entre cada muestra. En la práctica, nuestras frecuencias de muestreo serán del orden de cientos de kHz a decenas de MHz o incluso más. Cuando muestreamos señales, debemos tener en cuenta la frecuencia de muestreo, es un parámetro muy importante.

Para aquellos que prefieren ver las matemáticas; deje que $S_n$ represente la muestra $n$ , generalmente un número entero que comienza en 0. Usando esta convención, el proceso de muestreo se puede representar matemáticamente como $S_n = S(nT)$ para valores enteros de $n$ . Es decir, evaluamos la señal analógica $S(t)$ en estos intervalos de $nT$ .

Muestreo de Nyquist¶

Para una señal determinada, la gran pregunta a menudo es ¿a qué velocidad debemos muestrear? Examinemos una señal que es simplemente una onda sinusoidal, de frecuencia f, que se muestra en verde a continuación. Digamos que tomamos muestras a una tasa Fs (las muestras se muestran en azul). Si muestreamos esa señal a una velocidad igual a f (es decir, Fs = f), obtendremos algo parecido a:

La línea discontinua roja en la imagen de arriba reconstruye una función diferente (incorrecta) que podría haber llevado a que se registraran las mismas muestras. Indica que nuestra frecuencia de muestreo era demasiado baja porque las mismas muestras podrían haber provenido de dos funciones diferentes, lo que genera ambigüedad. Si queremos reconstruir con precisión la señal original, no podemos tener esta ambigüedad.

Intentemos muestrear un poco más rápido, en Fs = 1,2f:

Una vez más, hay una señal diferente que podría encajar en estas muestras. Esta ambigüedad significa que si alguien nos diera esta lista de muestras, no podríamos distinguir qué señal era la original según nuestro muestreo.

¿Qué tal el muestreo a Fs = 1,5f?

Example of sampling ambiguity when a signal is not sampled fast enough (below the Nyquist rate)

¡Todavía no es lo suficientemente rápido! Según una parte de la teoría DSP en la que no profundizaremos, hay que muestrear al dos veces la frecuencia de la señal para eliminar la ambigüedad que estamos experimentando:

Esta vez no hay ninguna señal incorrecta porque muestreamos lo suficientemente rápido como para que no exista ninguna señal que se ajuste a estas muestras aparte de la que ves (a menos que vayas más alto en frecuencia, pero eso lo discutiremos más adelante).

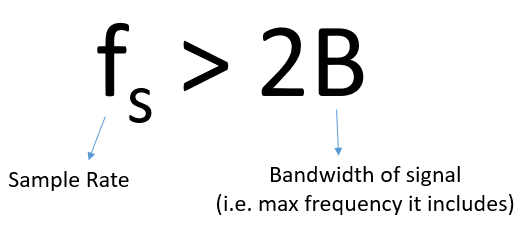
En el ejemplo anterior, nuestra señal era simplemente una onda sinusoidal, la mayoría de las señales reales tendrán muchos componentes de frecuencia. Para muestrear con precisión cualquier señal dada, la frecuencia de muestreo debe ser “al menos el doble de la frecuencia del componente de frecuencia máxima”. A continuación se muestra una visualización que utiliza un gráfico de ejemplo en el dominio de la frecuencia. Tenga en cuenta que siempre habrá un nivel de ruido mínimo, por lo que la frecuencia más alta suele ser una aproximación:

Nyquist sampling means that your sample rate is higher than the signal's maximum bandwidth

Debemos identificar el componente de frecuencia más alta, luego duplicarlo y asegurarnos de muestrear a esa velocidad o más rápido. La tasa mínima en la que podemos muestrear se conoce como Tasa Nyquist. En otras palabras, la tasa de Nyquist es la tasa mínima a la que se debe muestrear una señal (ancho de banda finito) para retener toda su información. Es una pieza teórica extremadamente importante dentro de DSP y SDR que sirve como puente entre señales continuas y discretas.

Si no tomamos muestras lo suficientemente rápido obtenemos algo llamado aliasing, que aprenderemos más adelante, pero tratamos de evitarlo a toda costa. Lo que hacen nuestros SDR (y la mayoría de los receptores en general) es filtrar todo lo que esté por encima de Fs/2 justo antes de realizar el muestreo. Si intentamos recibir una señal con una frecuencia de muestreo demasiado baja, ese filtro cortará parte de la señal. Nuestros SDR hacen todo lo posible para proporcionarnos muestras libres de aliasing y otras imperfecciones.

Muestreo en Cuadratura¶

El término “cuadratura” tiene muchos significados, pero en el contexto de DSP y SDR se refiere a dos ondas que están desfasadas 90 grados. ¿Por qué 90 grados desfasados? Considere cómo dos ondas que están desfasadas 180 grados son esencialmente la misma onda con uno multiplicado por -1. Al estar desfasadas 90 grados, se vuelven ortogonales, y hay muchas cosas interesantes que puedes hacer con funciones ortogonales. En aras de la simplicidad, utilizamos seno y coseno como nuestras dos ondas sinusoidales que están desfasadas 90 grados.

A continuación, asignemos variables para representar la amplitud del seno y el coseno. Usaremos $I$ para cos() y $Q$ para sin():

$I \cos(2\pi ft) Q \sin(2\pi ft)$

Podemos ver esto visualmente trazando I y Q iguales a 1:

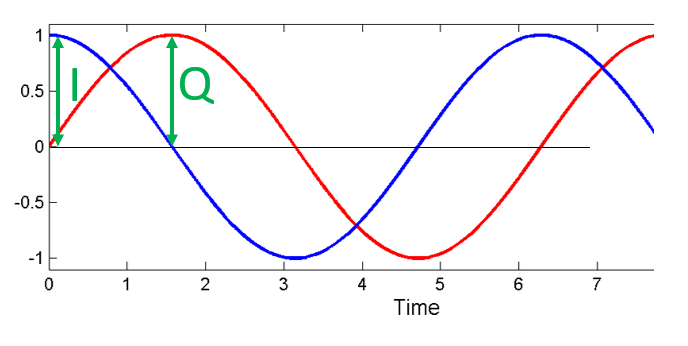
I and Q visualized as amplitudes of sinusoids that get summed together

Llamamos a cos() el componente “en fase”, de ahí el nombre I, y sin() es el componente fuera de fase o “cuadratura” de 90 grados, de ahí Q. Aunque si accidentalmente lo mezclas y asignas Q a el cos() y I al sin(), no hará ninguna diferencia en la mayoría de las situaciones.

El muestreo de IQ se entiende más fácilmente si se utiliza el punto de vista del transmisor, es decir, considerando la tarea de transmitir una señal de RF a través del aire. Queremos enviar una única onda sinusoidal en una determinada fase, lo que se puede hacer enviando la suma de sin() y cos() con una fase de 0, debido a la identidad trigonométrica: $a \cos( x) + b \sin(x) = A \cos(x-\phi)$ . Digamos que x(t) es nuestra señal a transmitir:

$x(t) = I \cos(2\pi ft) + Q \sin(2\pi ft)$

¿Qué pasa cuando sumamos un seno y un coseno? O mejor dicho, ¿qué sucede cuando sumamos dos sinusoides que están desfasadas 90 grados? En el vídeo a continuación, hay un control deslizante para ajustar I y otro para ajustar Q. Lo que se traza es el coseno, el seno y luego la suma de los dos.

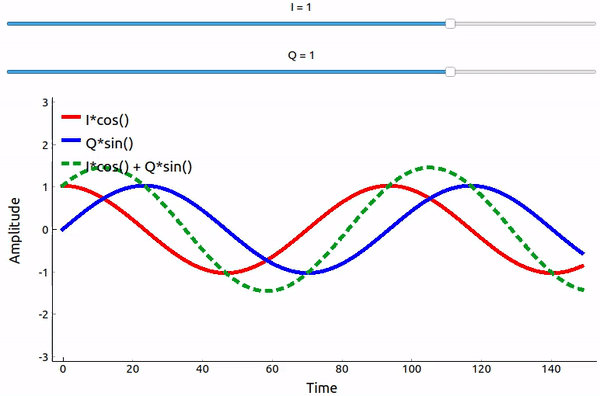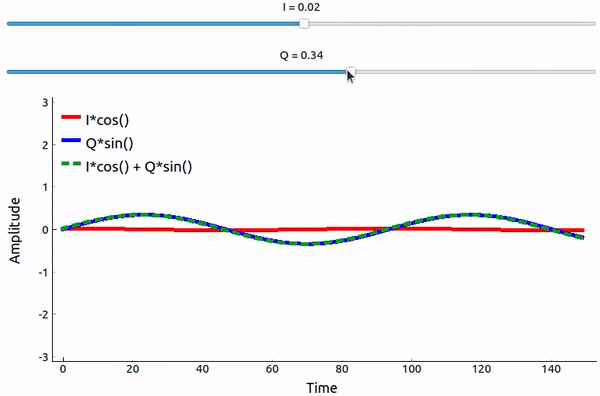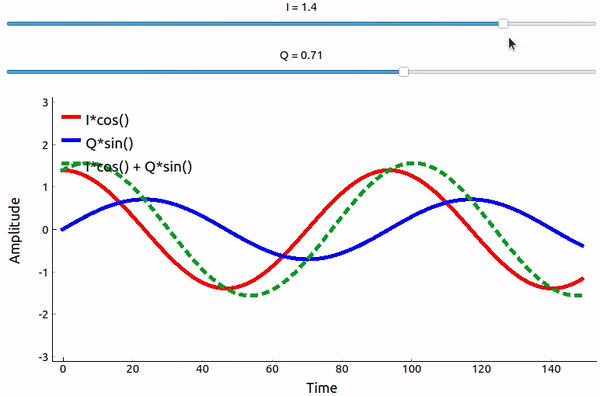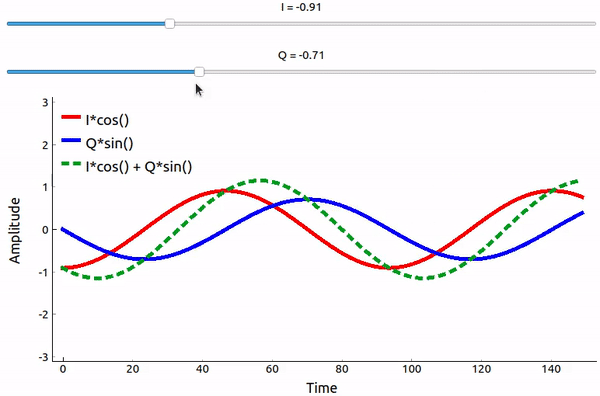
GNU Radio animation showing I and Q as amplitudes of sinusoids that get summed together

(El código utilizado para esta aplicación Python basada en pyqtgraph se puede encontrar aqui)

Lo importante es que cuando sumamos cos() y sin(), obtenemos otra onda sinusoidal pura con una fase y amplitud diferentes. Además, la fase cambia a medida que quitamos o añadimos lentamente una de las dos partes. La amplitud también cambia. Todo esto es el resultado de la identidad trigonométrica: $a \cos(x) + b \sin(x) = A \cos(x-\phi)$ , a la que volveremos en un momento. La “utilidad” de este comportamiento es que podemos controlar la fase y la amplitud de una onda sinusoidal resultante ajustando las amplitudes I y Q (no tenemos que ajustar la fase del coseno o del seno). Por ejemplo, podríamos ajustar I y Q de manera que mantengamos la amplitud constante y hagamos la fase como queramos. Como transmisor, esta capacidad es extremadamente útil porque sabemos que necesitamos transmitir una señal sinusoidal para que vuele por el aire como una onda electromagnética. Y es mucho más fácil ajustar dos amplitudes y realizar una operación de suma en comparación con ajustar una amplitud y una fase. El resultado es que nuestro transmisor se verá así:

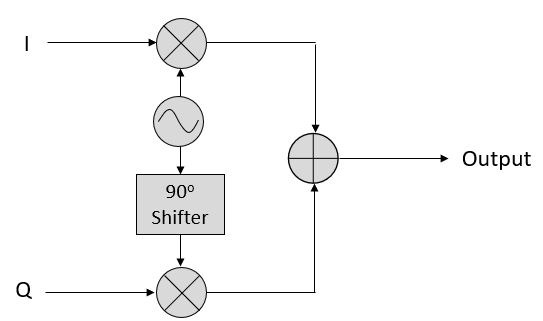
Diagram showing how I and Q are modulated onto a carrier

Sólo necesitamos generar una onda sinusoidal y desplazarla 90 grados para obtener la porción Q.

Numeros Complejos¶

En última instancia, la convención IQ es una forma alternativa de representar magnitud y fase, lo que nos lleva a números complejos y la capacidad de representarlos en un plano complejo. Es posible que hayas visto números complejos antes en otras clases. Tome el número complejo 0,7-0,4j como ejemplo:

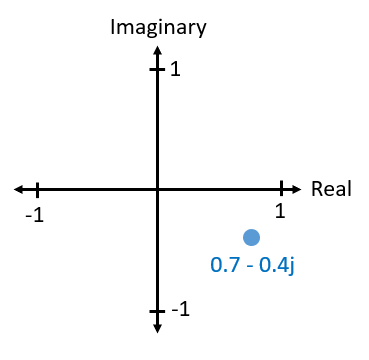
Un número complejo es en realidad sólo dos números juntos, una porción real y otra imaginaria. Un número complejo también tiene magnitud y fase, lo que tiene más sentido si lo consideramos como un vector en lugar de un punto. La magnitud es la longitud de la línea entre el origen y el punto (es decir, la longitud del vector), mientras que la fase es el ángulo entre el vector y 0 grados, que definimos como el eje real positivo:

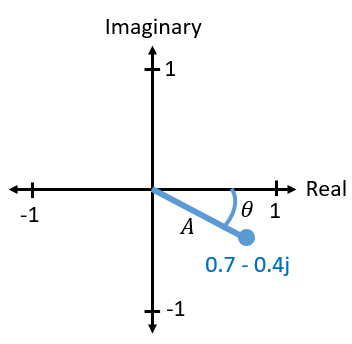
Esta representación de una sinusoide se conoce como “diagrama fasorial”. Se trata simplemente de trazar números complejos y tratarlos como vectores. Ahora, ¿cuál es la magnitud y la fase de nuestro número complejo de ejemplo 0,7-0,4j? Para un número complejo dado donde $a$ es la parte real y $b$ es la parte imaginaria:

$\mathrm{magnitude} = \sqrt{a^2 + b^2} = 0.806 \mathrm{phase} = \tan^{-1} \left( \frac{b}{a} \right) = -29.7^{\circ} = -0.519 \quad \mathrm{radians}$

En Python puedes usar np.abs(x) y np.angle(x) para la magnitud y la fase. La entrada puede ser un número complejo o una matriz de números complejos, y la salida será un número real (del tipo de datos flotante).

Quizás ya hayas descubierto cómo se relaciona este diagrama vectorial o fasorial con la convención IQ: I es real y Q es imaginario. A partir de este momento, cuando dibujemos el plano complejo, lo etiquetaremos con I y Q en lugar de real e imaginario. ¡Siguen siendo números complejos!

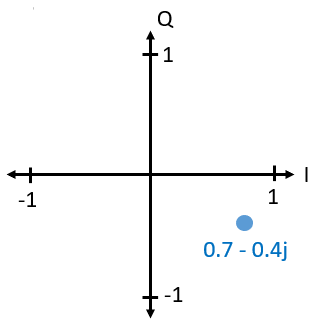
Ahora digamos que queremos transmitir nuestro punto de ejemplo 0.7-0.4j. Estaremos transmitiendo:

$x(t) = I \cos(2\pi ft) + Q \sin(2\pi ft) \quad \quad \quad = 0.7 \cos(2\pi ft) - 0.4 \sin(2\pi ft)$

Nosotros podemos usar la identidad trigonométrica $a \cos(x) + b \sin(x) = A \cos(x-\phi)$ donde $A$ ¿Se encuentra nuestra magnitud con $\sqrt{I^2 + Q^2}$ y $\phi$ es nuestra fase, igual a $\tan^{-1} \left( Q/I \right)$ . La ecuación anterior ahora se convierte en:

$x(t) = 0.806 \cos(2\pi ft + 0.519)$

Aunque empezamos con un número complejo, lo que estamos transmitiendo es una señal real con cierta magnitud y fase; En realidad, no se puede transmitir algo imaginario con ondas electromagnéticas. Simplemente usamos números imaginarios/complejos para representar lo que se esta transmitiendo. Hablaremos sobre la $f$ pronto.

Numeros complejos en FFTs¶

Se supuso que los números complejos anteriores eran muestras en el dominio del tiempo, pero también se encontrará con números complejos cuando realice una FFT. Cuando cubrimos el último capítulo de las series de Fourier y las FFT, aún no nos habíamos sumergido en números complejos. Cuando toma la FFT de una serie de muestras, encuentra la representación en el dominio de la frecuencia. Hablamos de cómo la FFT determina qué frecuencias existen en ese conjunto de muestras (la magnitud de la FFT indica la fuerza de cada frecuencia). Pero lo que también hace la FFT es calcular el retraso (desplazamiento de tiempo) necesario para aplicar a cada una de esas frecuencias, de modo que el conjunto de sinusoides pueda sumarse para reconstruir la señal en el dominio del tiempo. Ese retraso es simplemente la fase de la FFT. La salida de una FFT es una matriz de números complejos, y cada número complejo le da la magnitud y la fase, y el índice de ese número le da la frecuencia. Si genera sinusoides en esas frecuencias/magnitudes/fases y las suma, obtendrá su señal original en el dominio del tiempo (o algo muy cercano a ella, y ahí es donde entra en juego el teorema de muestreo de Nyquist).

Lado del Receptor¶

Ahora tomemos la perspectiva de un receptor de radio que intenta recibir una señal (por ejemplo, una señal de radio FM). Usando el muestreo de IQ, el diagrama ahora se ve así:

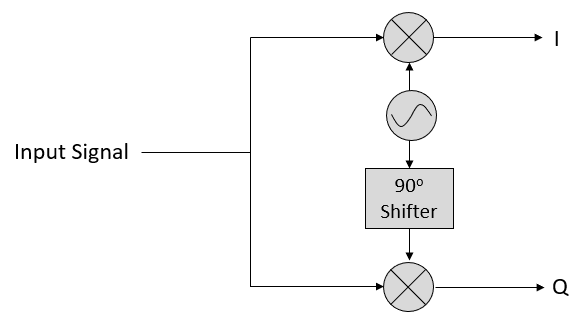
Receiving IQ samples by directly multiplying the input signal by a sine wave and a 90 degree shifted version of that sine wave

Lo que entra es una señal real recibida por nuestra antena, y esas se transforman en valores de IQ. Lo que hacemos es muestrear las ramas I y Q individualmente, usando dos ADC, y luego combinamos los pares y los almacenamos como números complejos. En otras palabras, en cada paso de tiempo, tomará una muestra de un valor I y un valor Q y los combinará en la forma $I + jQ$ (es decir, un número complejo por muestra de coeficiente intelectual). Siempre habrá una “frecuencia de muestreo”, la velocidad a la que se realiza el muestreo. Alguien podría decir: “Tengo un SDR funcionando a una frecuencia de muestreo de 2 MHz”. Lo que quieren decir es que el SDR recibe dos millones de muestras de coeficiente intelectual por segundo.

Si alguien te da un montón de muestras de coeficiente intelectual, se verá como una matriz/vector 1D de números complejos. Este punto, complejo o no, es el objetivo de todo este capítulo, y finalmente lo logramos.

A lo largo de este libro de texto, se familiarizará mucho con cómo funcionan las muestras de IQ, cómo recibirlas y transmitirlas con un SDR, cómo procesarlas en Python y cómo guardarlas en un archivo para su posterior análisis.

Una última nota importante: la figura anterior muestra lo que sucede dentro del SDR. En realidad, no tenemos que generar una onda sinusoidal, desplazarla 90, multiplicarla o sumarla: el SDR lo hace por nosotros. Le decimos al SDR a qué frecuencia queremos muestrear o a qué frecuencia queremos transmitir nuestras muestras. Del lado del receptor, el SDR nos proporcionará las muestras de IQ. Para el lado de transmisión, tenemos que proporcionar al SDR las muestras de IQ. En términos de tipo de datos, serán enteros complejos o flotantes.

Portadora y Downconversion¶

Hasta este punto no hemos discutido la frecuencia, pero vimos que había una $f$ en las ecuaciones que involucran cos() y sin(). Esta frecuencia es la frecuencia central de la señal que enviamos a través del aire (la frecuencia de la onda electromagnética). Nos referimos a él como “portadora” porque transporta nuestra señal en una determinada frecuencia de RF. Cuando sintonizamos una frecuencia con nuestro SDR y las muestras recibidas, nuestra información se almacena en I y Q; este operador no aparece en I y Q, suponiendo que sintonicemos el operador.

Figure made with TikZ

Como referencia, las señales de radio como radio FM, WiFi, Bluetooth, LTE, GPS, etc., suelen utilizar una frecuencia (es decir, una portadora) entre 100 MHz y 6 GHz. Estas frecuencias viajan muy bien por el aire, pero no requieren antenas muy largas ni mucha potencia para transmitir o recibir. Tu microondas cocina alimentos con ondas electromagnéticas a 2,4 GHz. Si hay una fuga en la puerta, su microondas bloqueará las señales WiFi y posiblemente también le queme la piel. Otra forma de ondas electromagnéticas es la luz. La luz visible tiene una frecuencia de alrededor de 500 THz. Es tan alto que no utilizamos antenas tradicionales para transmitir luz. Utilizamos métodos como los LED, que son dispositivos semiconductores. Crean luz cuando los electrones saltan entre las órbitas atómicas del material semiconductor, y el color depende de qué tan lejos saltan. Técnicamente, la radiofrecuencia (RF) se define como el rango de aproximadamente 20 kHz a 300 GHz. Estas son las frecuencias a las que la energía de una corriente eléctrica oscilante puede irradiarse desde un conductor (una antena) y viajar a través del espacio. El rango de 100 MHz a 6 GHz son las frecuencias más útiles, al menos para la mayoría de las aplicaciones modernas. Las frecuencias superiores a 6 GHz se han utilizado para comunicaciones por radar y por satélite durante décadas, y ahora se utilizan en 5G “mmWave” (24 - 29 GHz) para complementar las bandas inferiores y aumentar las velocidades.

Cuando cambiamos los valores de IQ rápidamente y transmitimos nuestra portadora, se llama “modular” la portadora (con datos o lo que queramos). Cuando cambiamos I y Q, cambiamos la fase y amplitud de la portadora. Otra opción es cambiar la frecuencia de la portadora, es decir, subirla o bajarla ligeramente, que es lo que hace la radio FM.

Como ejemplo simple, digamos que transmitimos la muestra de IQ 1+0j y luego cambiamos a transmitir 0+1j. pasamos de enviar $\cos(2\pi ft)$ to $\sin(2\pi ft)$ , lo que significa que nuestro portador cambia de fase 90 grados cuando cambiamos de una muestra a otra.

Es fácil confundirse entre la señal que queremos transmitir (que normalmente contiene muchos componentes de frecuencia) y la frecuencia en la que la transmitimos (nuestra frecuencia portadora). Es de esperar que esto se aclare cuando cubramos las señales de banda base versus señales de paso de banda.

Ahora volvamos al muestreo por un segundo. En lugar de recibir muestras multiplicando lo que sale de la antena por cos() y sin() y luego registrar I y Q, ¿qué pasaría si introdujéramos la señal de la antena en un solo ADC, como en la arquitectura de muestreo directo que acabamos de discutir? Digamos que la frecuencia del operador es de 2,4 GHz, como WiFi o Bluetooth. Eso significa que tendríamos que tomar muestras a 4,8 GHz, como aprendimos. ¡Eso es extremadamente rápido! Un ADC que toma muestras tan rápido cuesta miles de dólares. En lugar de eso, “convertimos hacia abajo” la señal para que la señal que queremos muestrear esté centrada alrededor de CC o 0 Hz. Esta conversión descendente ocurre antes de que tomemos la muestra. Partimos de:

$I \cos(2\pi ft) Q \sin(2\pi ft)$

a solo I y Q.

Visualicemos la downconversion en el dominio de la frecuencia:

The downconversion process where a signal is frequency shifted from RF to 0 Hz or baseband

Cuando nos centramos en 0 Hz, la frecuencia máxima ya no es 2,4 GHz sino que se basa en las características de la señal desde que eliminamos la portadora. La mayoría de las señales tienen un ancho de banda de entre 100 kHz y 40 MHz, por lo que mediante el downconversion podemos muestrear a una velocidad mucho más baja. Tanto el B2X0 USRP como el PlutoSDR contienen un circuito integrado de RF (RFIC) que puede muestrear hasta 56 MHz, que es lo suficientemente alto para la mayoría de las señales que encontraremos.

Sólo para reiterar, el proceso de downconversion lo realiza nuestro SDR; Como usuario del SDR no tenemos que hacer nada más que decirle qué frecuencia sintonizar. La downconversion (y upconversion) se realiza mediante un componente llamado mezclador, generalmente representado en diagramas como un símbolo de multiplicación dentro de un círculo. El mezclador recibe una señal, emite la señal convertida hacia abajo o hacia arriba y tiene un tercer puerto que se utiliza para alimentar un oscilador. La frecuencia del oscilador determina el cambio de frecuencia aplicado a la señal, y el mezclador es esencialmente solo una función de multiplicación (recuerde que multiplicar por una sinusoide provoca un cambio de frecuencia).

Por último, es posible que sienta curiosidad por saber qué tan rápido viajan las señales por el aire. Recuerde la clase de física del colegio donde las ondas de radio son más que ondas electromagnéticas de bajas frecuencias (entre aproximadamente 3 kHz y 80 GHz). La luz visible también son ondas electromagnéticas, en frecuencias mucho más altas (400 THz a 700 THz). Todas las ondas electromagnéticas viajan a la velocidad de la luz, que es de aproximadamente 3,8 m/s, al menos cuando viajan a través del aire o el vacío. Ahora bien, como siempre viajan a la misma velocidad, la distancia que recorre la onda en una oscilación completa (un ciclo completo de la onda sinusoidal) depende de su frecuencia. A esta distancia la llamamos longitud de onda, denotada como $\lambda$ . Probablemente hayas visto esta relación antes:

$f = \frac{c}{\lambda}$

donde $c$ es la velocidad de la luz, normalmente establecida en 3e8 cuando $f$ es en Hz y $\lambda$ es en metros. En las comunicaciones inalámbricas esta relación cobra importancia cuando llegamos a las antenas, porque para recibir una señal en una determinada frecuencia portadora, $f$ , necesitas una antena que coincida con su longitud de onda, $\lambda$ , comunmente la antena es $\lambda/2$ o $\lambda/4$ en longitud. Sin embargo, independientemente de la frecuencia/longitud de onda, la información transportada en esa señal siempre viajará a la velocidad de la luz, desde el transmisor hasta el receptor. Al calcular este retraso a través del aire, una regla general es que la luz viaja aproximadamente un pie en un nanosegundo. Otra regla general: una señal que viaja hacia un satélite en órbita geoestacionaria y regresa tardará aproximadamente 0,25 segundos en todo el viaje.

Arquitectura del Receptor¶

La figura de la sección del “lado del receptor” muestra cómo la señal de entrada se convierte y se divide en I y Q. Esta disposición se denomina “conversión directa” o “IF cero”, porque las frecuencias de RF se convierten directamente a banda base. Otra opción es no realizar ninguna conversión descendente y muestrear tan rápido para capturar todo, desde 0 Hz hasta la mitad de la frecuencia de muestreo. Esta estrategia se denomina “muestreo directo” o “RF directa” y requiere un chip ADC extremadamente costoso. Una tercera arquitectura, que es popular porque así funcionaban las radios antiguas, que se conoce como “superheterodina”. Implica una conversión descendente, pero no hasta 0 Hz. Coloca la señal de interés en una frecuencia intermedia, conocida como “IF”. Un amplificador de bajo ruido (LNA) es simplemente un amplificador diseñado para señales de potencia extremadamente baja en la entrada. Aquí están los diagramas de bloques de estas tres arquitecturas, tenga en cuenta que también existen variaciones e híbridos de estas arquitecturas:

Three common receiver architectures: direct sampling, direct conversion, and superheterodyne

Señales Banda Base y Paso de Banda¶

Nos referimos a una señal centrada alrededor de 0 Hz como “banda base”. Por el contrario, “paso de banda” se refiere a cuando existe una señal en alguna frecuencia de RF que no se acerca a 0 Hz, y que se ha elevado con el propósito de transmisión inalámbrica. No existe la noción de “transmisión en banda base”, porque no se puede transmitir algo imaginario. Una señal en banda base puede estar perfectamente centrada a 0 Hz como en la parte derecha de la figura de la sección anterior. Podría estar cerca de 0 Hz, como las dos señales que se muestran a continuación. Esas dos señales todavía se consideran banda base. También se muestra un ejemplo de señal de paso de banda, centrada en una frecuencia muy alta denominada $f_c$ .

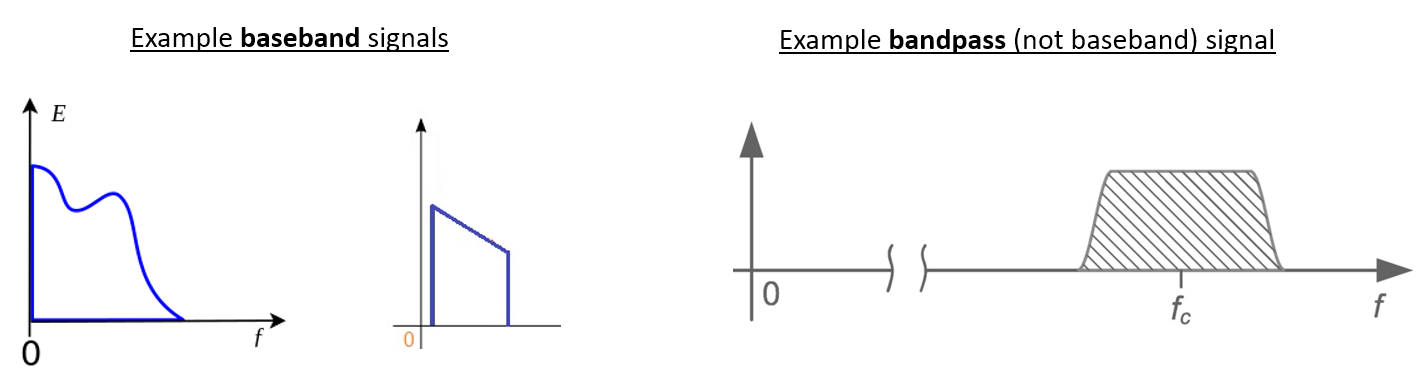
Es posible que también escuche el término frecuencia intermedia (abreviado como IF); Por ahora, piense en IF como un paso de conversión intermedio dentro de una radio entre banda base y paso de banda/RF.

Tendemos a crear, grabar o analizar señales en banda base porque podemos trabajar con una frecuencia de muestreo más baja (por las razones analizadas en la subsección anterior). Es importante tener en cuenta que las señales de banda base suelen ser señales complejas, mientras que las señales de paso de banda (por ejemplo, las señales que realmente transmitimos por RF) son reales. Piénselo: debido a que la señal transmitida a través de una antena debe ser real, no se puede transmitir directamente una señal compleja/imaginaria. Sabrá que una señal es definitivamente una señal compleja si las porciones de frecuencia negativa y positiva de la señal no son exactamente iguales. Después de todo, los números complejos son la forma en que representamos frecuencias negativas. En realidad no existen frecuencias negativas; es solo la porción de la señal debajo de la frecuencia portadora.

En la sección anterior, donde jugamos con el punto complejo 0,7 - 0,4j, era esencialmente una muestra en una señal de banda base. La mayoría de las veces ves muestras complejas (muestras de IQ), estás en banda base. Las señales rara vez se representan o almacenan digitalmente en RF, debido a la cantidad de datos que se necesitarían y al hecho de que normalmente solo nos interesa una pequeña porción del espectro de RF.

DC Spike and Offset Tuning¶

Una vez que comience a trabajar con SDR, a menudo encontrará un gran pico en el centro de la FFT. Se denomina “DC offset” o “DC spike” o, a veces, “fuga de LO”, donde LO significa oscilador local.

A continuación se muestra un ejemplo de DC spike:

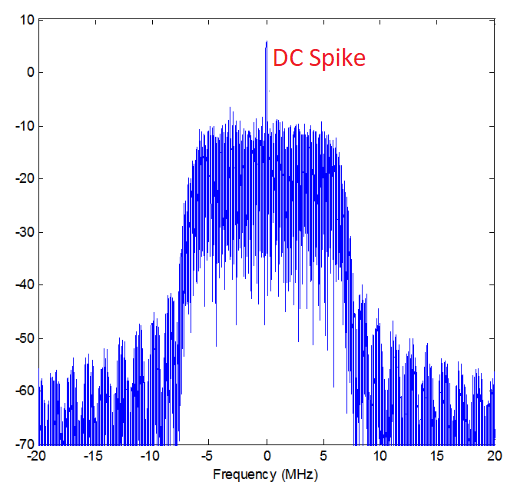
DC spike shown in a power spectral density (PSD)

Debido a que el SDR sintoniza una frecuencia central, la porción de 0 Hz de la FFT corresponde a la frecuencia central. Dicho esto, un pico DC no significa necesariamente que haya energía en la frecuencia central. Si solo hay un pico DC y el resto de la FFT parece ruido, lo más probable es que en realidad no haya una señal presente para mostrar.

Un desfase DC es un artefacto común en los receptores de conversión directa, que es la arquitectura utilizada para SDR como PlutoSDR, RTL-SDR, LimeSDR y muchos Ettus USRP. En los receptores de conversión directa, un oscilador, el LO, convierte la señal de su frecuencia real a banda base. Como resultado, la fuga de este LO aparece en el centro del ancho de banda observado. La fuga de LO es energía adicional creada mediante la combinación de frecuencias. Eliminar este ruido adicional es difícil porque está cerca de la señal de salida deseada. Muchos circuitos integrados de RF (RFIC) tienen una eliminación automática del desfase DC, pero generalmente requieren que haya una señal presente para funcionar. Es por eso que el pico DC será muy evidente cuando no haya señales presentes.

Una forma rápida de manejar el desfase DC es sobremuestrear la señal y desafinarla. Como ejemplo, digamos que queremos ver 5 MHz de espectro a 100 MHz. En cambio, lo que podemos hacer es muestrear a 20 MHz con una frecuencia central de 95 MHz.

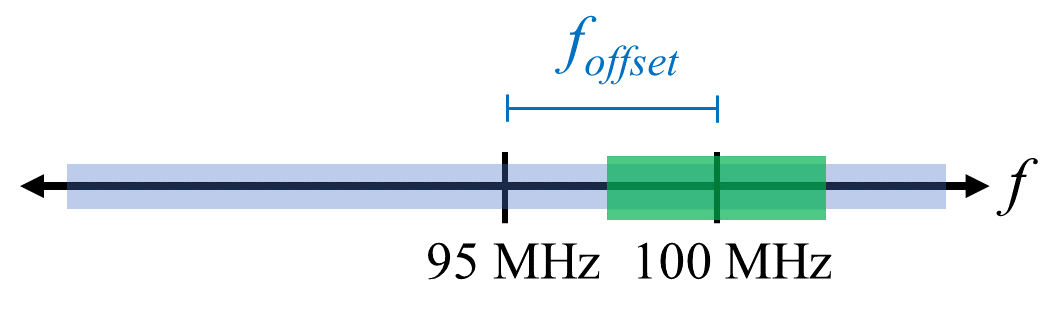
The offset tuning process to avoid the DC spike

El cuadro azul de arriba muestra lo que realmente muestra el SDR, y el cuadro verde muestra la porción del espectro que queremos. Nuestro LO se configurará en 95 MHz porque esa es la frecuencia a la que le pedimos que sintonice el SDR. Dado que 95 MHz está fuera del cuadro verde, no obtendremos ningún pico DC.

Hay un problema: si queremos que nuestra señal esté centrada en 100 MHz y solo contenga 5 MHz, tendremos que realizar un cambio de frecuencia, filtrar y reducir la resolución de la señal nosotros mismos (algo que aprenderemos a hacer más adelante). Afortunadamente, este proceso de desafinación, también conocido como aplicación de un desplazamiento LO, a menudo está integrado en los SDR, donde automáticamente realizarán una desafinación y luego cambiarán la frecuencia a la frecuencia central deseada. Nos beneficiamos cuando el SDR puede hacerlo internamente: no tenemos que enviar una frecuencia de muestreo más alta a través de nuestra conexión USB o Ethernet, lo que obstaculiza la frecuencia de muestreo que podemos usar.

Esta subsección sobre compensación DC es un buen ejemplo de en qué se diferencia este libro de texto de otros. Un libro de texto promedio sobre DSP analizará el muestreo, pero tiende a no incluir obstáculos de implementación como las compensaciones de DC a pesar de su prevalencia en la práctica.

Muestreo usando nuestro SDR¶

Para obtener información específica de SDR sobre cómo realizar el muestreo, consulte uno de los siguientes capítulos:

Capitulo PlutoSDR en Python
Capitulo USRP en Python

Calcular la potencia promedio¶

En RF DSP, a menudo nos gusta calcular la potencia de una señal, como detectar la presencia de la señal antes de intentar realizar más DSP. Para una señal compleja discreta, es decir, una que hemos muestreado, podemos encontrar la potencia promedio tomando la magnitud de cada muestra, elevándola al cuadrado y luego encontrando la media:

$P = \frac{1}{N} \sum_{n=1}^{N} |x[n]|^2$

Recuerde que el valor absoluto de un número complejo es solo la magnitud, es decir, $\sqrt{I^2+Q^2}$

En Python, calcular la potencia promedio será así:

avg_pwr = np.mean(np.abs(x)**2)

Aquí tienes un truco muy útil para calcular la potencia media de una señal muestreada. Si su señal tiene una media aproximadamente cero, lo que suele ser el caso en SDR (veremos por qué más adelante), entonces la potencia de la señal se puede encontrar tomando la varianza de las muestras. En estas circunstancias, puedes calcular la potencia de esta manera en Python:

avg_pwr = np.var(x) # (signal should have roughly zero mean)

La razón por la cual la varianza de las muestras calcula la potencia promedio es bastante simple: la ecuación para la varianza es $\frac{1}{N}\sum^N_{n=1} |x[n]-\mu|^2$ donde $\mu$ es la media de la señal. ¡Esa ecuación me resulta familiar! Si $\mu$ es cero, entonces la ecuación para determinar la varianza de las muestras se vuelve equivalente a la ecuación de potencia. También puedes restar la media de las muestras en tu ventana de observación y luego tomar la varianza. Solo debes saber que si el valor medio no es cero, la varianza y la potencia no son iguales.

Calcular la Densidad Espectral de Potencia¶

En el último capítulo aprendimos que podemos convertir una señal al dominio de la frecuencia usando una FFT, y el resultado se llama densidad espectral de potencia (PSD). El PSD es una herramienta extremadamente útil para visualizar señales en el dominio de la frecuencia, y muchos algoritmos DSP se realizan en el dominio de la frecuencia. Pero para encontrar realmente la PSD de un lote de muestras y trazarla, hacemos más que simplemente tomar una FFT. Debemos realizar las siguientes seis operaciones para calcular PSD:

Tome la FFT de nuestras muestras. Si tenemos x muestras, el tamaño de FFT será la longitud de x de forma predeterminada. Usemos las primeras 1024 muestras como ejemplo para crear una FFT de tamaño 1024. El resultado serán 1.024 complejos de punto decimal.
Tome la magnitud de la salida FFT, que nos proporciona 1024 valores reales con parte decimal.
Eleva al cuadrado la magnitud resultante para obtener potencia.
Normalizar: dividir por el tamaño de FFT ( $N$ ) y frecuencia de muestreo ( $Fs$ ).
Convertir a dB usando $10 \log_{10}()$ ; Siempre vemos los PSD en escala logarítmica.
Realice un cambio FFT, cubierto en el capítulo anterior, para mover “0 Hz” en el centro y las frecuencias negativas a la izquierda del centro.

Esos seis pasos en Python son:

Fs = 1e6 # lets say we sampled at 1 MHz
# assume x contains your array of IQ samples
N = 1024
x = x[0:N] # we will only take the FFT of the first 1024 samples, see text below
PSD = np.abs(np.fft.fft(x))**2 / (N*Fs)
PSD_log = 10.0*np.log10(PSD)
PSD_shifted = np.fft.fftshift(PSD_log)

Opcionalmente podemos aplicar una ventana, como aprendimos en el capitulo Dominio de la Frecuencia. La ventana se produciría justo antes de la línea de código con fft().

# add the following line after doing x = x[0:1024]
x = x * np.hamming(len(x)) # apply a Hamming window

Para trazar este PSD necesitamos conocer los valores del eje x. Como aprendimos en el capítulo anterior, cuando muestreamos una señal, sólo “vemos” el espectro entre -Fs/2 y Fs/2, donde Fs es nuestra frecuencia de muestreo. La resolución que logramos en el dominio de la frecuencia depende del tamaño de nuestra FFT, que por defecto es igual al número de muestras en las que realizamos la operación FFT. En este caso, nuestro eje x tiene 1024 puntos igualmente espaciados entre -0,5 MHz y 0,5 MHz. Si hubiéramos sintonizado nuestro SDR a 2,4 GHz, nuestra ventana de observación estaría entre 2,3995 GHz y 2,4005 GHz. En Python, cambiar la ventana de observación se verá así:

center_freq = 2.4e9 # frequency we tuned our SDR to
f = np.arange(Fs/-2.0, Fs/2.0, Fs/N) # start, stop, step.  centered around 0 Hz
f += center_freq # now add center frequency
plt.plot(f, PSD_shifted)
plt.show()

¡Deberíamos quedarnos con un hermoso PSD!

Si desea encontrar el PSD de millones de muestras, no haga una FFT de un millón de puntos porque probablemente llevará una eternidad. Después de todo, le dará una salida de un millón de “contenedores de frecuencia”, lo cual es demasiado para mostrarlo en un gráfico. En su lugar, sugiero hacer varios PSD más pequeños y promediarlos juntos o mostrarlos usando un gráfico de espectrograma. Alternativamente, si sabe que su señal no cambia rápidamente, es adecuado usar algunos miles de muestras y encontrar la PSD de ellas; dentro de ese período de tiempo de unos pocos miles de muestras, probablemente capturará suficiente señal para obtener una buena representación.

A continuación se muestra un ejemplo de código completo que incluye la generación de una señal (exponencial compleja a 50 Hz) y ruido. Tenga en cuenta que N, el número de muestras a simular, se convierte en la longitud de FFT porque tomamos la FFT de toda la señal simulada.

import numpy as np
import matplotlib.pyplot as plt

Fs = 300 # sample rate
Ts = 1/Fs # sample period
N = 2048 # number of samples to simulate

t = Ts*np.arange(N)
x = np.exp(1j*2*np.pi*50*t) # simulates sinusoid at 50 Hz

n = (np.random.randn(N) + 1j*np.random.randn(N))/np.sqrt(2) # complex noise with unity power
noise_power = 2
r = x + n * np.sqrt(noise_power)

PSD = np.abs(np.fft.fft(r))**2 / (N*Fs)
PSD_log = 10.0*np.log10(PSD)
PSD_shifted = np.fft.fftshift(PSD_log)

f = np.arange(Fs/-2.0, Fs/2.0, Fs/N) # start, stop, step

plt.plot(f, PSD_shifted)
plt.xlabel("Frequency [Hz]")
plt.ylabel("Magnitude [dB]")
plt.grid(True)
plt.show()

Output:

Otras lecturas de sampling¶

http://rfic.eecs.berkeley.edu/~niknejad/ee242/pdf/eecs242_lect3_rxarch.pdf