17. Ejemplo Punto a Punto¶
En este capítulo reunimos muchos de los conceptos que aprendimos anteriormente y analizamos un ejemplo completo de recepción y decodificación de una señal digital real. Analizaremos el Radio Data System (RDS), que es un protocolo de comunicaciones para incorporar pequeñas cantidades de información en transmisiones de radio FM, como la estación y el nombre de la canción. Tendremos que demodular FM, cambiar de frecuencia, filtrar, diezmar, remuestrear, sincronizar, decodificar y analizar los bytes. Se proporciona un archivo IQ de ejemplo para fines de prueba o si no tiene un SDR a mano.
Introducción a la radio FM y RDS¶
Para entender el RDS primero debemos repasar las emisiones de radio FM y cómo estan estructuradas estas señales. Probablemente esté familiarizado con la parte de audio de las señales de FM, que son simplemente señales de audio moduladas en frecuencia y transmitidas en frecuencias centrales correspondientes al nombre de la estación, por ejemplo, “WPGC 95.5 FM” está centrada exactamente en 95,5 MHz. Además de la parte de audio, cada transmisión de FM contiene otros componentes que se modulan en frecuencia junto con el audio. En lugar de simplemente buscar en Google la estructura de la señal, echemos un vistazo a la densidad espectral de potencia (PSD) de una señal de FM de ejemplo, después de la demodulación de FM. Solo vemos la parte positiva porque la salida de la demodulación de FM es una señal real, aunque la entrada sea compleja (veremos el código para realizar esta demodulación en breve).
Al observar la señal en el dominio de la frecuencia, notamos las siguientes señales individuales:
- Una señal de alta potencia entre 0 - 17 kHz
- Un tono a 19 kHz
- Centrada en 38 kHz y aproximadamente 30 kHz de ancho, vemos una señal simétrica de aspecto interesante.
- Señal en forma de doble lóbulo centrada en 57 kHz
- Señal en forma de un solo lóbulo centrada en 67 kHz
Esto es esencialmente todo lo que podemos determinar con solo mirar el PSD, y recuerde que esto es después de la demodulación de FM. El PSD antes de la demodulación de FM se parece a lo siguiente, lo que realmente no nos dice mucho.
Dicho esto, es importante entender que cuando modulas una señal en FM, una frecuencia más alta en la señal de datos conducirá a una frecuencia más alta en la señal de FM resultante. Por lo tanto, la presencia de una señal centrada en 67 kHz aumenta el ancho de banda total ocupado por la señal de FM transmitida, ya que el componente de frecuencia máxima ahora es de alrededor de 75 kHz, como se muestra en el primer PSD anterior. La reglas del ancho de banda de Carson aplicado a FM nos dice que las estaciones de FM ocupan aproximadamente 250 kHz de espectro, razón por la cual generalmente tomamos muestras a 250 kHz (recuerde que cuando usamos muestreo en cuadratura/IQ, el ancho de banda recibido es igual a su frecuencia de muestreo).
Como comentario breve, algunos lectores pueden estar familiarizados con observar la banda de FM usando un SDR o un analizador de espectro y ver su espectrograma, y pensar que las señales de bloque y adyacentes a algunas de las estaciones de FM son RDS.
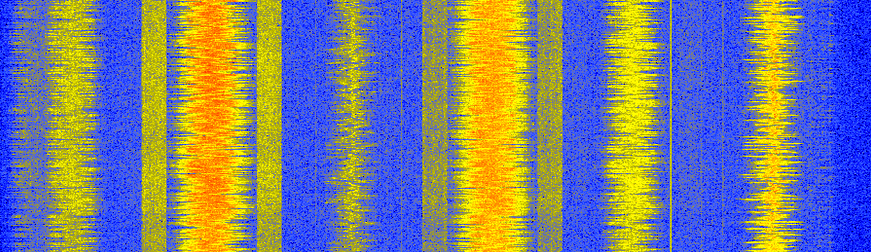
Resulta que esas señales en bloque son en realidad HD Radio, una versión digital de la misma señal de radio FM (mismo contenido de audio). Esta versión digital genera una señal de audio de mayor calidad en el receptor porque la FM analógica siempre incluirá algo de ruido después de la demodulación, ya que es un esquema analógico, pero la señal digital se puede demodular/decodificar con cero ruido, suponiendo que no haya errores de bits.
Volvamos a las cinco señales que descubrimos en nuestro PSD; el siguiente diagrama se etiqueta para qué se utiliza cada señal.
Repasando cada una de estas señales sin ningún orden en particular:
Las señales de audio mono y estéreo simplemente transportan la señal de audio, en un patrón en el que sumarlas y restarlas da como resultado los canales izquierdo y derecho.
El tono piloto de 19 kHz se utiliza para demodular el audio estéreo. Si duplicas el tono actúa como referencia de frecuencia y fase, ya que la señal de audio estéreo está centrada en 38 kHz. Se puede duplicar el tono simplemente elevando al cuadrado las muestras; recuerde la propiedad de Fourier de cambio de frecuencia que aprendimos en el capitulo Dominio de la Frecuencia .
DirectBand era una red de transmisión de datos inalámbrica de América del Norte propiedad de Microsoft y operada por ella, también llamada “MSN Direct” en los mercados de consumo. DirectBand transmitía información a dispositivos como receptores GPS portátiles, relojes de pulsera y estaciones meteorológicas domésticas. Incluso permitía a los usuarios recibir mensajes cortos desde Windows Live Messenger. Una de las aplicaciones más exitosas de DirectBand fueron los datos de tráfico local en tiempo real mostrados en los receptores GPS Garmin, que eran utilizados por millones de personas antes de que los teléfonos inteligentes se volvieran omnipresentes. El servicio DirectBand se cerró en enero de 2012, lo que plantea la pregunta: ¿por qué lo vemos en nuestra señal de FM grabada después de 2012? Mi única suposición es que la mayoría de los transmisores de FM fueron diseñados y construidos mucho antes de 2012, e incluso sin ninguna “suministro” activo por DirectBand, todavía transmite algo, tal vez símbolos piloto.
Por último, llegamos a RDS, que es el foco del resto de este capítulo. Como podemos ver en nuestro primer PSD, RDS tiene aproximadamente 4 kHz de ancho de banda (antes de ser modulado en FM) y se encuentra entre el audio estéreo y la señal DirectBand. Es un protocolo de comunicaciones digitales de baja velocidad de datos que permite a las estaciones de FM incluir identificación de la estación, información del programa, hora y otra información diversa junto con el audio. El estándar RDS se publica como estándar IEC 62106 y se puede encontrar aqui.
La señal RDS¶
En este capítulo usaremos Python para recibir RDS, pero para comprender mejor cómo recibirlo, primero debemos aprender cómo se forma y transmite la señal.
Lado de transmisión¶
La información RDS que transmitirá la estación de FM (por ejemplo, nombre de pista, etc.) está codificada en conjuntos de 8 bytes. Cada conjunto de 8 bytes, que corresponde a 64 bits, se combina con 40 “bits de verificación” para formar un único “grupo”. Estos 104 bits se transmiten juntos, aunque no hay un intervalo de tiempo entre los grupos, por lo que desde la perspectiva del receptor recibe estos bits sin parar y debe determinar el límite entre los grupos de 104 bits. Veremos más detalles sobre la codificación y la estructura del mensaje una vez que nos sumerjamos en el lado de la recepción.
Para transmitir estos bits de forma inalámbrica, RDS utiliza BPSK, que como aprendimos en el capitulo Modulación Digital es un esquema de modulación digital simple que se utiliza para asignar unos y ceros a la fase de una portadora. Como muchos protocolos basados en BPSK, RDS utiliza codificación diferencial, lo que simplemente significa que los 1 y 0 de los datos se codifican en cambios de 1 y 0, lo que le permite ya no preocuparse si está desfasado 180 grados (más sobre esto más adelante). Los símbolos BPSK se transmiten a 1187,5 símbolos por segundo y, debido a que BPSK transporta un bit por símbolo, eso significa que RDS tiene una velocidad de datos sin procesar de aproximadamente 1,2 kbps (incluida la sobrecarga). RDS no contiene ninguna codificación de canal (también conocida como corrección de errores directa), aunque los paquetes de datos contienen una verificación de redundancia cíclica (CRC) para saber cuándo ocurrió un error.
Luego, la señal BPSK final se cambia de frecuencia hasta 57 kHz y se agrega a todos los demás componentes de la señal de FM, antes de ser modulada en FM y transmitida por aire en la frecuencia de la estación. Las señales de radio FM se transmiten a una potencia extremadamente alta en comparación con la mayoría de las demás comunicaciones inalámbricas, ¡hasta 80 kW! Esta es la razón por la que muchos usuarios de SDR tienen un filtro de rechazo de FM (es decir, un filtro de eliminación de banda) en línea con su antena; por lo que FM no añade interferencias a lo que están intentando recibir.
Si bien esto fue solo una breve descripción general del lado de la transmisión, profundizaremos en más detalles cuando hablemos de la recepción de RDS.
La de recepción¶
Para demodular y decodificar RDS, realizaremos los siguientes pasos, muchos de los cuales son pasos del lado de transmisión a la inversa (no es necesario memorizar esta lista, recorreremos cada paso individualmente a continuación):
- Reciba una señal de radio FM centrada en la frecuencia de la estación (o lea en una grabación de IQ), generalmente a una frecuencia de muestreo de 250 kHz
- Demodular la FM usando lo que se llama “demodulación en cuadratura”
- Cambio de frecuencia de 57 kHz para que la señal RDS esté centrada en 0 Hz
- Filtro de paso bajo, para filtrar todo excepto RDS (también actúa como filtro combinado)
- Diezmar por 10 para que podamos trabajar con una frecuencia de muestreo más baja, ya que de todos modos filtramos las frecuencias más altas.
- Remuestrear a 19 kHz lo que nos dará un número entero de muestras por símbolo
- Sincronización de tiempo a nivel de símbolo, usando Mueller y Muller en este ejemplo
- Sincronización fina de frecuencia mediante un bucle Costas
- Demodular el BPSK a 1 y 0
- Decodificación diferencial, para deshacer la codificación diferencial que se aplicó
- Decodificación de los 1 y 0 en grupos de bytes
- Análisis de los grupos de bytes en nuestro resultado final.
Si bien esto puede parecer muchos pasos, RDS es en realidad uno de los protocolos de comunicaciones digitales inalámbricas más simples que existen. Un protocolo inalámbrico moderno como WiFi o 5G requiere un libro de texto completo para cubrir solo la información de la capa PHY/MAC de alto nivel.
Ahora profundizaremos en el código Python utilizado para recibir RDS. Este código ha sido probado para funcionar usando una Grabación de radio FM que puedes encontrar aquí., aunque debería poder transmitir su propia señal siempre que se reciba con una SNR lo suficientemente alta, simplemente sintonice la frecuencia central de la estación y muestree a una velocidad de 250 kHz. Para maximizar la potencia de la señal recibida (por ejemplo, si está en interiores), es útil utilizar una antena dipolo de media onda de la longitud correcta (~1,5 metros), no las antenas de 2,4 GHz que vienen con Pluto. Dicho esto, FM es una señal muy fuerte y, si estás cerca de una ventana o afuera, las antenas de 2,4 GHz probablemente serán suficientes para captar las estaciones de radio más potentes.
En esta sección presentaremos pequeñas porciones del código individualmente, con discusión, pero el mismo código se proporciona al final de este capítulo en un bloque grande. Cada sección presentará un bloque de código y luego explicará lo que está haciendo.
Adquirir una señal¶
import numpy as np
from scipy.signal import resample_poly, firwin, bilinear, lfilter
import matplotlib.pyplot as plt
# Read in signal
x = np.fromfile('/home/marc/Downloads/fm_rds_250k_1Msamples.iq', dtype=np.complex64)
sample_rate = 250e3
center_freq = 99.5e6
Leemos en nuestra grabación de prueba, que fue muestreada a 250 kHz y centrada en una estación de FM recibida con una SNR alta. Asegúrese de actualizar la ruta del archivo para reflejar su sistema y dónde guardó la grabación. Si ya tiene un SDR configurado y funcionando desde Python, no dude en recibir una señal en vivo, aunque es útil haber probado primero todo el código con un known-to-work IQ recording. A lo largo de este código usaremos x para almacenar la señal actual que se está manipulando.
Demodulación FM¶
# Quadrature Demod
x = 0.5 * np.angle(x[0:-1] * np.conj(x[1:])) # see https://wiki.gnuradio.org/index.php/Quadrature_Demod
Como se analizó al principio de este capítulo, varias señales individuales se combinan en frecuencia y se modulan en FM para crear lo que realmente se transmite a través del aire. Entonces el primer paso es deshacer esa modulación FM. Otra forma de pensarlo es que la información se almacena en la variación de frecuencia de la señal que recibimos, y queremos demodularla para que la información ahora esté en amplitud, no en frecuencia. Tenga en cuenta que la salida de esta demodulación es una señal real, aunque hayamos introducido una señal compleja.
Lo que hace esta única línea de Python es primero calcular el producto de nuestra señal con una versión retardada y conjugada de nuestra señal. A continuación, encuentra la fase de cada muestra en ese resultado, que es el momento en el que pasa de complejo a real. Para demostrarnos que esto nos da la información contenida en las variaciones de frecuencia, consideremos un tono en la frecuencia \(f\) con alguna fase arbitraria \(\phi\), que podemos representar como \(e^ {j2 \pi (ft + \phi)}\). Cuando se trata de tiempo discreto, que utiliza un número entero \(n\) en lugar de \(t\), esto se convierte en \(e^{j2 \pi (f n + \phi)}\). La versión conjugada y retrasada es \(e^{-j2 \pi (f (n-1) + \phi)}\). Multiplicar estos dos lleva a \(e^{j2 \pi f}\), lo cual es genial porque \(\phi\) desapareció, y cuando calculamos la fase de esa expresión nos queda solo \(f\).
Un efecto secundario conveniente de la modulación FM es que las variaciones de amplitud de la señal recibida en realidad no cambian el volumen del audio, a diferencia de la radio AM.
Dezplazamiento en frecuencia¶
# Freq shift
N = len(x)
f_o = -57e3 # amount we need to shift by
t = np.arange(N)/sample_rate # time vector
x = x * np.exp(2j*np.pi*f_o*t) # down shift
A continuación bajamos la frecuencia en 57 kHz, usando el truco \(e^{j2 \pi f_ot}\) que aprendimos en el capítulo Sincronización donde f_o es el cambio de frecuencia en Hz y t es solo un vector de tiempo, el hecho de que comience en 0 no es importante, lo que importa es que use el período de muestreo correcto (que es inverso a la frecuencia de muestreo). Además, debido a que se trata de una señal real, en realidad no importa si usas -57 o +57 kHz porque las frecuencias negativas coinciden con las positivas, por lo que de cualquier manera cambiaremos nuestro RDS a 0. Hz.
Filtrar para aislar RDS¶
# Low-Pass Filter
taps = firwin(numtaps=101, cutoff=7.5e3, fs=sample_rate)
x = np.convolve(x, taps, 'valid')
Ahora debemos filtrar todo excepto RDS. Como tenemos RDS centrado en 0 Hz, eso significa que lo que queremos es un filtro paso bajo. Usamos firwin() para diseñar un filtro FIR (es decir, encontrar los taps), que solo necesita saber cuántos taps queremos que tenga el filtro y la frecuencia de corte. También se debe proporcionar la frecuencia de muestreo o, de lo contrario, la frecuencia de corte no tiene sentido para firwin. El resultado es un filtro paso bajo simétrico, por lo que sabemos que las derivaciones serán números reales y podemos aplicar el filtro a nuestra señal mediante una convolución. Elegimos 'valid' para deshacernos de los efectos de borde de hacer convolución, aunque en este caso realmente no importa porque estamos alimentando una señal tan larga que algunas muestras extrañas en cada borde son innecesarias. No voy a desperdiciar nada.
Nota al margen: en algún momento actualizaré el filtro anterior para usar un filtro coincidente adecuado (creo que el coseno elevado de raíz es lo que usa RDS), por razones conceptuales, pero obtuve las mismas tasas de error usando el enfoque firwin() que un apropiado filtro de acoplamiento de GNU Radio, por lo que claramente no es un requisito estricto.
Decimate por 10¶
# Decimate by 10, now that we filtered and there wont be aliasing
x = x[::10]
sample_rate = 25e3
Cada vez que filtra hasta una pequeña fracción de su ancho de banda (por ejemplo, comenzamos con 125 kHz de ancho de banda real y ahorramos solo 7,5 kHz de eso), tiene sentido diezmar. Recuerde el comienzo del capítulo Muestreo IQ donde aprendimos sobre la frecuencia Nyquist y cómo almacenar completamente información de banda limitada siempre que muestreemos al doble de la frecuencia más alta. Bueno, ahora que usamos nuestro filtro paso bajo, nuestra frecuencia más alta es de aproximadamente 7,5 kHz, por lo que solo necesitamos una frecuencia de muestreo de 15 kHz. Sólo para estar seguros agregaremos algo de margen y usaremos una nueva frecuencia de muestreo de 25 kHz (esto terminará funcionando bien matemáticamente más adelante).
Realizamos la diezma simplemente descartando 9 de cada 10 muestras, ya que anteriormente teníamos una frecuencia de muestreo de 250 kHz y ahora queremos que sea de 25 kHz. Esto puede parecer confuso al principio, porque descartar el 90% de las muestras parece como si estuvieras descartando información, pero si revisas el capítulo Muestreo IQ verás por qué en realidad no estamos perdiendo nada, porque Se filtró correctamente (que actuó como nuestro filtro anti-aliasing) y redujo nuestra frecuencia máxima y, por lo tanto, el ancho de banda de la señal.
Desde la perspectiva del código, este es probablemente el paso más simple de todos, pero asegúrese de actualizar su variable sample_rate para reflejar la nueva frecuencia de muestreo.
Remuestreo a 19 kHz¶
# Resample to 19kHz
x = resample_poly(x, 19, 25) # up, down
sample_rate = 19e3
En el capítulo Formador de Pulso afianzamos el concepto de “muestras por símbolo” y aprendimos la conveniencia de tener un número entero de muestras por símbolo (un valor fraccionario es válido, pero no conveniente). Como se mencionó anteriormente, RDS utiliza BPSK y transmite 1187,5 símbolos por segundo. Si continuamos usando nuestra señal tal como está, muestreada a 25 kHz, tendremos 21.052631579 muestras por símbolo (haga una pausa y piense en los cálculos si eso no tiene sentido). Entonces, lo que realmente queremos es una frecuencia de muestreo que sea un múltiplo entero de 1187,5 Hz, pero no podemos bajarla demasiado o no podremos “almacenar” el ancho de banda completo de nuestra señal. En la subsección anterior hablamos de que necesitamos una frecuencia de muestreo de 15 kHz o superior, y elegimos 25 kHz sólo para darnos algo de margen.
Encontrar la mejor frecuencia de muestreo para remuestrear se reduce a cuántas muestras por símbolo queremos, y podemos trabajar hacia atrás. Hipotéticamente, consideremos apuntar a 10 muestras por símbolo. La velocidad de símbolo RDS de 1187,5 multiplicada por 10 nos daría una frecuencia de muestreo de 11,875 kHz, que lamentablemente no es lo suficientemente alta para Nyquist. ¿Qué tal 13 muestras por símbolo? 1187,5 multiplicado por 13 nos da 15437,5 Hz, que está por encima de 15 kHz, pero es un número bastante impar. ¿Qué tal la siguiente potencia de 2, es decir, 16 muestras por símbolo? ¡1187,5 multiplicado por 16 es exactamente 19 kHz! El número par es menos una coincidencia y más una elección de diseño de protocolo.
Para remuestrear de 25 kHz a 19 kHz, usamos resample_poly() que aumenta la muestra con un valor entero, filtra y luego reduce la muestra con un valor entero. Esto es conveniente porque en lugar de ingresar 25000 y 19000 podemos usar 25 y 19. Si hubiéramos usado 13 muestras por símbolo usando una frecuencia de muestreo de 15437,5 Hz, no podríamos usar resample_poly() y el proceso de remuestreo sería mucho más complicado.
Una vez más, recuerde siempre actualizar su variable sample_rate cuando realice una operación que la cambie.
Sincronización en Tiempo (Símbolo-Nivel)¶
# Symbol sync, using what we did in sync chapter
samples = x # for the sake of matching the sync chapter
samples_interpolated = resample_poly(samples, 32, 1) # we'll use 32 as the interpolation factor, arbitrarily chosen, seems to work better than 16
sps = 16
mu = 0.01 # initial estimate of phase of sample
out = np.zeros(len(samples) + 10, dtype=np.complex64)
out_rail = np.zeros(len(samples) + 10, dtype=np.complex64) # stores values, each iteration we need the previous 2 values plus current value
i_in = 0 # input samples index
i_out = 2 # output index (let first two outputs be 0)
while i_out < len(samples) and i_in+32 < len(samples):
out[i_out] = samples_interpolated[i_in*32 + int(mu*32)] # grab what we think is the "best" sample
out_rail[i_out] = int(np.real(out[i_out]) > 0) + 1j*int(np.imag(out[i_out]) > 0)
x = (out_rail[i_out] - out_rail[i_out-2]) * np.conj(out[i_out-1])
y = (out[i_out] - out[i_out-2]) * np.conj(out_rail[i_out-1])
mm_val = np.real(y - x)
mu += sps + 0.01*mm_val
i_in += int(np.floor(mu)) # round down to nearest int since we are using it as an index
mu = mu - np.floor(mu) # remove the integer part of mu
i_out += 1 # increment output index
x = out[2:i_out] # remove the first two, and anything after i_out (that was never filled out)
Finalmente estamos listos para nuestra sincronización de símbolo/tiempo, aquí usaremos exactamente el mismo código de sincronización de reloj de Mueller y Muller del capítulo Sincronización, consúltelo si desea obtener más información sobre cómo funciona. Establecemos la muestra por símbolo (sps) en 16 como se analizó anteriormente. Mediante experimentación se descubrió que un valor de ganancia de mu de 0,01 funciona bien. La salida ahora debería ser una muestra por símbolo, es decir, nuestra salida son nuestros “símbolos suaves”, con posible compensación de frecuencia incluida. La siguiente animación del gráfico de constelación se utiliza para verificar que estamos obteniendo símbolos BPSK (con un desplazamiento de frecuencia que causa rotación):
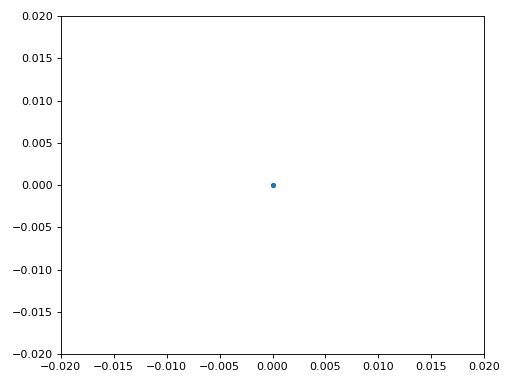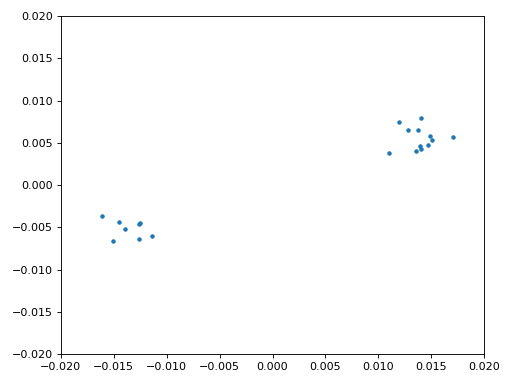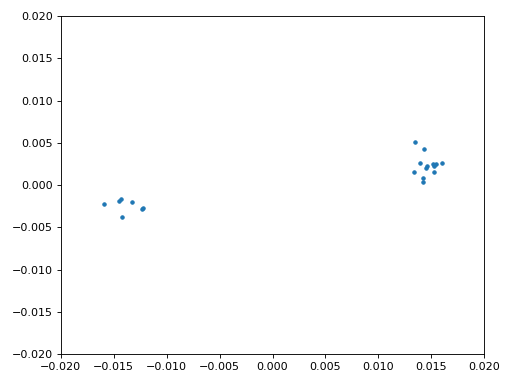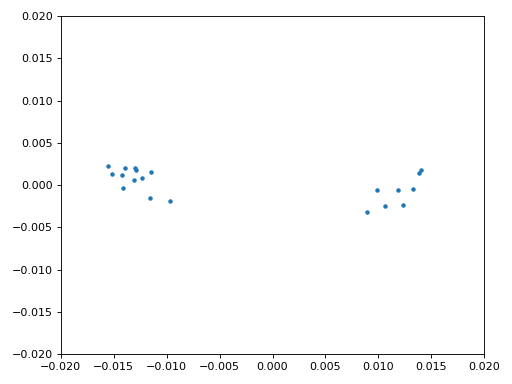
Si está utilizando su propia señal de FM y no obtiene dos grupos distintos de muestras complejas en este punto, significa que la sincronización del símbolo anterior no logró sincronizarse o que hay algún problema con uno de los pasos anteriores. No es necesario animar la constelación, pero si graficarlas, asegúrate de evitar graficar todas las muestras, porque simplemente se verá como un círculo. Si traza sólo 100 o 200 muestras a la vez, tendrá una mejor idea de si están en dos grupos o no, incluso si están girando.
Sincronización en Frecuencia Fina¶
# Fine freq sync
samples = x # for the sake of matching the sync chapter
N = len(samples)
phase = 0
freq = 0
# These next two params is what to adjust, to make the feedback loop faster or slower (which impacts stability)
alpha = 8.0
beta = 0.002
out = np.zeros(N, dtype=np.complex64)
freq_log = []
for i in range(N):
out[i] = samples[i] * np.exp(-1j*phase) # adjust the input sample by the inverse of the estimated phase offset
error = np.real(out[i]) * np.imag(out[i]) # This is the error formula for 2nd order Costas Loop (e.g. for BPSK)
# Advance the loop (recalc phase and freq offset)
freq += (beta * error)
freq_log.append(freq * sample_rate / (2*np.pi)) # convert from angular velocity to Hz for logging
phase += freq + (alpha * error)
# Optional: Adjust phase so its always between 0 and 2pi, recall that phase wraps around every 2pi
while phase >= 2*np.pi:
phase -= 2*np.pi
while phase < 0:
phase += 2*np.pi
x = out
También copiaremos el código Python de sincronización fina en frecuencia del capítulo Sincronización, que utiliza Costas Loop para eliminar cualquier desplazamiento de frecuencia residual, así como alinear nuestro BPSK con el eje real (I), forzando Q sea lo más cercano posible a cero. Cualquier cosa que quede en Q probablemente se deba al ruido en la señal, suponiendo que el bucle de Costas esté sintonizado correctamente. Solo por diversión, veamos la misma animación que arriba excepto después de que se haya realizado la sincronización de frecuencia (¡no más giros!):
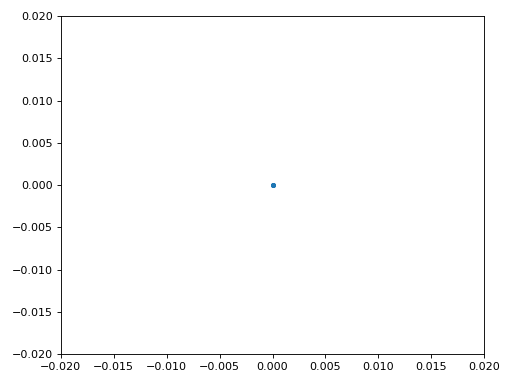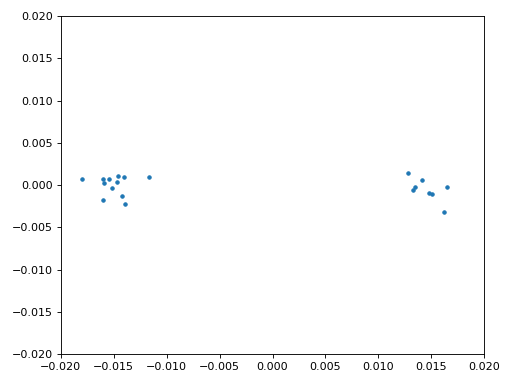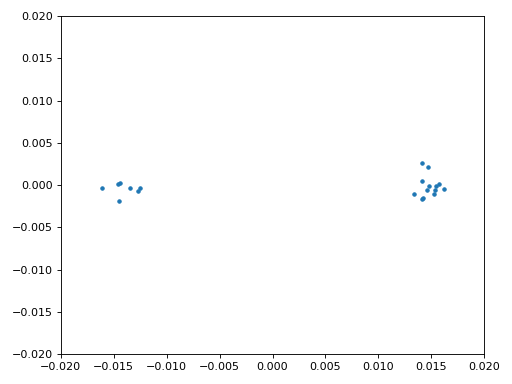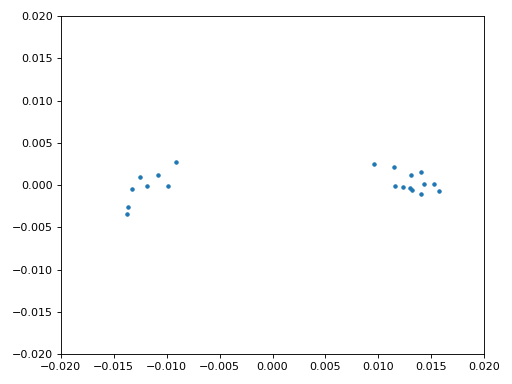
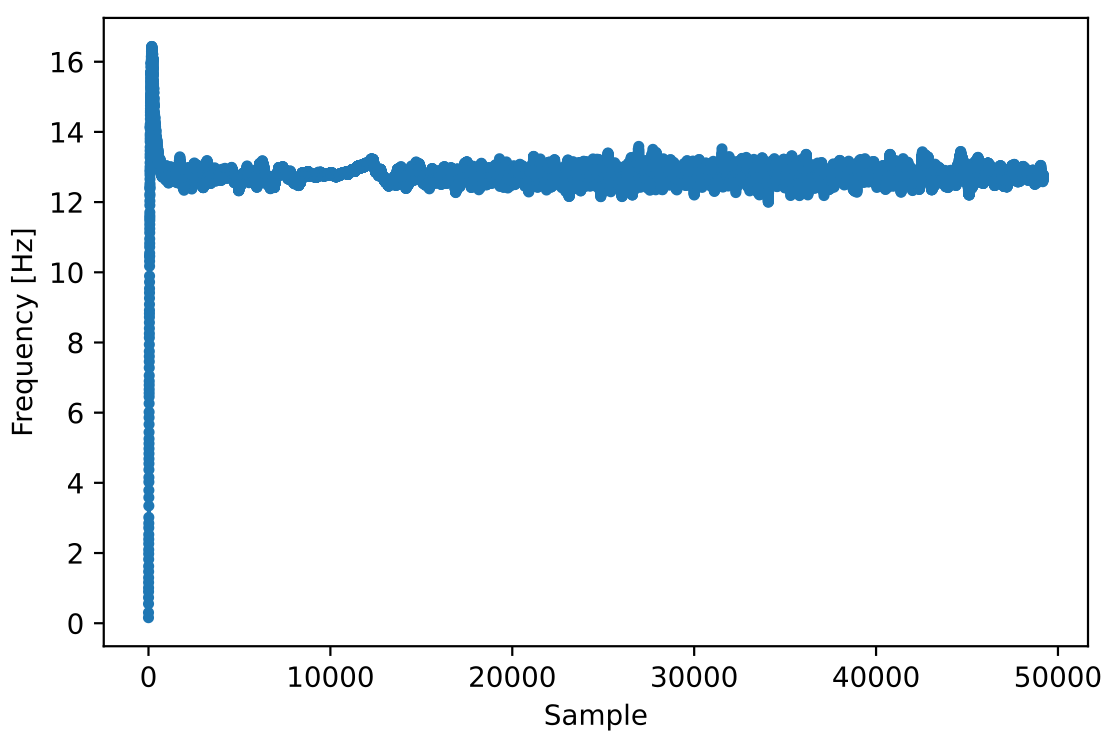
Además, podemos observar el error de frecuencia estimado a lo largo del tiempo para ver cómo funcionamiento de Costas Loop; observe cómo lo registramos en el código anterior. Parece que hubo alrededor de 13 Hz de compensación de frecuencia, ya sea debido a que el oscilador/LO del transmisor estaba apagado o al LO del receptor (muy probablemente el receptor). Si está utilizando su propia señal de FM, es posible que necesite modificar alpha y beta hasta que la curva se vea similar; debería lograr la sincronización con bastante rapidez (por ejemplo, unos cientos de símbolos) y mantenerla con mínima oscilación. El patrón que ve a continuación después de encontrar su estado estable es fluctuación de frecuencia, no oscilación.
Demodulación BPSK¶
# Demod BPSK
bits = (np.real(x) > 0).astype(int) # 1's and 0's
Demodular el BPSK en este punto es muy fácil, recuerde que cada muestra representa un símbolo suave, por lo que todo lo que tenemos que hacer es verificar si cada muestra está por encima o por debajo de 0. El .astype(int) es así podemos trabajar con una serie de enteros en lugar de una serie de booleanos. Quizás te preguntes si por encima o por debajo de cero representa un 1 o un 0. Como verás en el siguiente paso, ¡no importa!
Decodificación diferencial¶
# Differential decoding, so that it doesn't matter whether our BPSK was 180 degrees rotated without us realizing it
bits = (bits[1:] - bits[0:-1]) % 2
bits = bits.astype(np.uint8) # for decoder
La señal BPSK utilizó codificación diferencial cuando se creó, lo que significa que cada 1 y 0 de los datos originales se transformó de manera que un cambio de 1 a 0 o de 0 a 1 se asignó a un 1, y ningún cambio se asignó a un 0. El gran beneficio de usar codificación diferencial es que no tienes que preocuparte por las rotaciones de 180 grados al recibir el BPSK, porque si consideramos que un 1 es mayor que cero o menor que cero ya no es un impacto, lo que importa es cambiando entre 1 y 0. Este concepto podría ser más fácil de entender si observa datos de ejemplo; a continuación se muestran los primeros 10 símbolos antes y después de la decodificación diferencial:
[1 1 1 1 0 1 0 0 1 1] # before differential decoding
[- 0 0 0 1 1 1 0 1 0] # after differential decoding
Decodificación RDS¶
¡Finalmente tenemos nuestros fragmentos de información y estamos listos para decodificar lo que significan! El enorme bloque de código que se proporciona a continuación es lo que usaremos para decodificar los 1 y 0 en grupos de bytes. Esta parte tendría mucho más sentido si primero creáramos la parte del transmisor de RDS, pero por ahora solo sepa que en RDS, los bytes se agrupan en grupos de 12 bytes, donde los primeros 8 representan los datos y los últimos 4 actúan como un palabra de sincronización (llamadas “palabras desplazadas”). Los últimos 4 bytes no son necesarios para el siguiente paso (el analizador), por lo que no los incluimos en la salida. Este bloque de código toma los 1 y 0 creados anteriormente (en forma de una matriz 1D de uint8) y genera una lista de listas de bytes (una lista de 8 bytes donde esos 8 bytes están en una lista). Esto lo hace conveniente para el siguiente paso, que recorrerá la lista de 8 bytes, un grupo de 8 a la vez.
La mayor parte del código de decodificación real a continuación gira en torno a la sincronización (a nivel de bytes, no de símbolos) y la verificación de errores. Funciona en bloques de 104 bits, cada bloque se recibe correctamente o con error (usando CRC para verificar), y cada 50 bloques verifica si más de 35 de ellos se recibieron con error, en cuyo caso reinicia todo e intenta sincronizar nuevamente. El CRC se realiza mediante una verificación de 10 bits, con polinomio \(x^{10}+x^8+x^7+x^5+x^4+x^3+1\); esto ocurre cuando reg se aplica xor con 0x5B9, que es el equivalente binario de ese polinomio. En Python, los operadores bit a bit para [y, o, no, xor] son & | ~ ^ respectivamente, exactamente igual que C++. Un desplazamiento de bit a la izquierda es x << y (igual que multiplicar x por 2**y), y un desplazamiento de bit a la derecha es x >> y (igual que dividir x por 2** y), también como en C++.
Tenga en cuenta que no necesita revisar todo este código, ni nada de él, especialmente si se está concentrando en aprender el lado de la capa física (PHY) de DSP y SDR, ya que esto no representa la señal. Procesando. Este código es simplemente una implementación de un decodificador RDS y, esencialmente, nada de él puede reutilizarse para otros protocolos, porque es muy específico de la forma en que funciona RDS. Si ya está algo agotado con este capítulo, siéntase libre de saltarse este enorme bloque de código que tiene un trabajo bastante simple pero lo hace de una manera compleja.
# Constants
syndrome = [383, 14, 303, 663, 748]
offset_pos = [0, 1, 2, 3, 2]
offset_word = [252, 408, 360, 436, 848]
# see Annex B, page 64 of the standard
def calc_syndrome(x, mlen):
reg = 0
plen = 10
for ii in range(mlen, 0, -1):
reg = (reg << 1) | ((x >> (ii-1)) & 0x01)
if (reg & (1 << plen)):
reg = reg ^ 0x5B9
for ii in range(plen, 0, -1):
reg = reg << 1
if (reg & (1 << plen)):
reg = reg ^ 0x5B9
return reg & ((1 << plen) - 1) # select the bottom plen bits of reg
# Initialize all the working vars we'll need during the loop
synced = False
presync = False
wrong_blocks_counter = 0
blocks_counter = 0
group_good_blocks_counter = 0
reg = np.uint32(0) # was unsigned long in C++ (64 bits) but numpy doesn't support bitwise ops of uint64, I don't think it gets that high anyway
lastseen_offset_counter = 0
lastseen_offset = 0
# the synchronization process is described in Annex C, page 66 of the standard */
bytes_out = []
for i in range(len(bits)):
# in C++ reg doesn't get init so it will be random at first, for ours its 0s
# It was also an unsigned long but never seemed to get anywhere near the max value
# bits are either 0 or 1
reg = np.bitwise_or(np.left_shift(reg, 1), bits[i]) # reg contains the last 26 rds bits. these are both bitwise ops
if not synced:
reg_syndrome = calc_syndrome(reg, 26)
for j in range(5):
if reg_syndrome == syndrome[j]:
if not presync:
lastseen_offset = j
lastseen_offset_counter = i
presync = True
else:
if offset_pos[lastseen_offset] >= offset_pos[j]:
block_distance = offset_pos[j] + 4 - offset_pos[lastseen_offset]
else:
block_distance = offset_pos[j] - offset_pos[lastseen_offset]
if (block_distance*26) != (i - lastseen_offset_counter):
presync = False
else:
print('Sync State Detected')
wrong_blocks_counter = 0
blocks_counter = 0
block_bit_counter = 0
block_number = (j + 1) % 4
group_assembly_started = False
synced = True
break # syndrome found, no more cycles
else: # SYNCED
# wait until 26 bits enter the buffer */
if block_bit_counter < 25:
block_bit_counter += 1
else:
good_block = False
dataword = (reg >> 10) & 0xffff
block_calculated_crc = calc_syndrome(dataword, 16)
checkword = reg & 0x3ff
if block_number == 2: # manage special case of C or C' offset word
block_received_crc = checkword ^ offset_word[block_number]
if (block_received_crc == block_calculated_crc):
good_block = True
else:
block_received_crc = checkword ^ offset_word[4]
if (block_received_crc == block_calculated_crc):
good_block = True
else:
wrong_blocks_counter += 1
good_block = False
else:
block_received_crc = checkword ^ offset_word[block_number] # bitwise xor
if block_received_crc == block_calculated_crc:
good_block = True
else:
wrong_blocks_counter += 1
good_block = False
# Done checking CRC
if block_number == 0 and good_block:
group_assembly_started = True
group_good_blocks_counter = 1
group = bytearray(8) # 8 bytes filled with 0s
if group_assembly_started:
if not good_block:
group_assembly_started = False
else:
# raw data bytes, as received from RDS. 8 info bytes, followed by 4 RDS offset chars: ABCD/ABcD/EEEE (in US) which we leave out here
# RDS information words
# block_number is either 0,1,2,3 so this is how we fill out the 8 bytes
group[block_number*2] = (dataword >> 8) & 255
group[block_number*2+1] = dataword & 255
group_good_blocks_counter += 1
#print('group_good_blocks_counter:', group_good_blocks_counter)
if group_good_blocks_counter == 5:
#print(group)
bytes_out.append(group) # list of len-8 lists of bytes
block_bit_counter = 0
block_number = (block_number + 1) % 4
blocks_counter += 1
if blocks_counter == 50:
if wrong_blocks_counter > 35: # This many wrong blocks must mean we lost sync
print("Lost Sync (Got ", wrong_blocks_counter, " bad blocks on ", blocks_counter, " total)")
synced = False
presync = False
else:
print("Still Sync-ed (Got ", wrong_blocks_counter, " bad blocks on ", blocks_counter, " total)")
blocks_counter = 0
wrong_blocks_counter = 0
A continuación se muestra un ejemplo de resultado de este paso de decodificación. Observe cómo en este ejemplo se sincronizó con bastante rapidez pero luego pierde la sincronización un par de veces por algún motivo, aunque aún puede analizar todos los datos, como veremos. Si está utilizando el archivo de muestra descargable de 1M, solo verá las primeras líneas a continuación. El contenido real de estos bytes simplemente parece números/caracteres aleatorios dependiendo de cómo los muestre, pero en el siguiente paso los analizaremos para convertirlos en información legible por humanos.
Sync State Detected
Still Sync-ed (Got 0 bad blocks on 50 total)
Still Sync-ed (Got 0 bad blocks on 50 total)
Still Sync-ed (Got 0 bad blocks on 50 total)
Still Sync-ed (Got 0 bad blocks on 50 total)
Still Sync-ed (Got 1 bad blocks on 50 total)
Still Sync-ed (Got 5 bad blocks on 50 total)
Still Sync-ed (Got 26 bad blocks on 50 total)
Lost Sync (Got 50 bad blocks on 50 total)
Sync State Detected
Still Sync-ed (Got 3 bad blocks on 50 total)
Still Sync-ed (Got 0 bad blocks on 50 total)
Still Sync-ed (Got 0 bad blocks on 50 total)
Still Sync-ed (Got 0 bad blocks on 50 total)
Still Sync-ed (Got 0 bad blocks on 50 total)
Still Sync-ed (Got 0 bad blocks on 50 total)
Still Sync-ed (Got 0 bad blocks on 50 total)
Still Sync-ed (Got 0 bad blocks on 50 total)
Still Sync-ed (Got 0 bad blocks on 50 total)
Still Sync-ed (Got 0 bad blocks on 50 total)
Still Sync-ed (Got 0 bad blocks on 50 total)
Still Sync-ed (Got 0 bad blocks on 50 total)
Still Sync-ed (Got 0 bad blocks on 50 total)
Still Sync-ed (Got 0 bad blocks on 50 total)
Still Sync-ed (Got 0 bad blocks on 50 total)
Still Sync-ed (Got 0 bad blocks on 50 total)
Still Sync-ed (Got 0 bad blocks on 50 total)
Still Sync-ed (Got 0 bad blocks on 50 total)
Still Sync-ed (Got 0 bad blocks on 50 total)
Still Sync-ed (Got 0 bad blocks on 50 total)
Still Sync-ed (Got 0 bad blocks on 50 total)
Still Sync-ed (Got 0 bad blocks on 50 total)
Still Sync-ed (Got 2 bad blocks on 50 total)
Still Sync-ed (Got 1 bad blocks on 50 total)
Still Sync-ed (Got 20 bad blocks on 50 total)
Lost Sync (Got 47 bad blocks on 50 total)
Sync State Detected
Still Sync-ed (Got 32 bad blocks on 50 total)
Análisis RDS¶
Ahora que tenemos bytes, en grupos de 8, podemos extraer los datos finales, es decir, el resultado final que sea comprensible para los humanos. Esto se conoce como análisis de bytes y, al igual que el decodificador de la sección anterior, es simplemente una implementación del protocolo RDS y en realidad no es tan importante entenderlo. Por suerte no es un montón de código, si no incluyes las dos tablas definidas al principio, que son simplemente las tablas de búsqueda para el tipo de canal FM y el área de cobertura.
Para aquellos que quieran aprender cómo funciona este código, les proporcionaré información adicional. El protocolo utiliza este concepto de indicador A/B, lo que significa que algunos mensajes están marcados como A y otros como B, y el análisis cambia según cuál (si es A o B se almacena en el tercer bit del segundo byte). También utiliza diferentes tipos de “grupo” que son análogos al tipo de mensaje, y en este código solo estamos analizando el tipo de mensaje 2, que es el tipo de mensaje que tiene el texto de radio, que es la parte interesante, es el texto que se desplaza por la pantalla de su automóvil. Aún podremos analizar el tipo de canal y la región, ya que están almacenados en cada mensaje. Por último, tenga en cuenta que radiotext es una cadena que se inicializa en todos los espacios, se completa lentamente a medida que se analizan los bytes y luego se restablece en todos los espacios si se recibe un conjunto específico de bytes. Si tiene curiosidad sobre qué otros tipos de mensajes existen, la lista es: [“BASIC”, “PIN/SL”, “RT”, “AID”, “CT”, “TDC”, “IH”, “RP”, ” TMC”, “EWS”, “EON”]. El mensaje “RT” es radiotexto que es el único que decodificamos. El bloque RDS GNU Radio también decodifica “BASIC”, pero para las estaciones que utilicé para probar no contenía mucha información interesante y habría agregado muchas líneas al código siguiente.
# Annex F of RBDS Standard Table F.1 (North America) and Table F.2 (Europe)
# Europe North America
pty_table = [["Undefined", "Undefined"],
["News", "News"],
["Current Affairs", "Information"],
["Information", "Sports"],
["Sport", "Talk"],
["Education", "Rock"],
["Drama", "Classic Rock"],
["Culture", "Adult Hits"],
["Science", "Soft Rock"],
["Varied", "Top 40"],
["Pop Music", "Country"],
["Rock Music", "Oldies"],
["Easy Listening", "Soft"],
["Light Classical", "Nostalgia"],
["Serious Classical", "Jazz"],
["Other Music", "Classical"],
["Weather", "Rhythm & Blues"],
["Finance", "Soft Rhythm & Blues"],
["Children’s Programmes", "Language"],
["Social Affairs", "Religious Music"],
["Religion", "Religious Talk"],
["Phone-In", "Personality"],
["Travel", "Public"],
["Leisure", "College"],
["Jazz Music", "Spanish Talk"],
["Country Music", "Spanish Music"],
["National Music", "Hip Hop"],
["Oldies Music", "Unassigned"],
["Folk Music", "Unassigned"],
["Documentary", "Weather"],
["Alarm Test", "Emergency Test"],
["Alarm", "Emergency"]]
pty_locale = 1 # set to 0 for Europe which will use first column instead
# page 72, Annex D, table D.2 in the standard
coverage_area_codes = ["Local",
"International",
"National",
"Supra-regional",
"Regional 1",
"Regional 2",
"Regional 3",
"Regional 4",
"Regional 5",
"Regional 6",
"Regional 7",
"Regional 8",
"Regional 9",
"Regional 10",
"Regional 11",
"Regional 12"]
radiotext_AB_flag = 0
radiotext = [' ']*65
first_time = True
for group in bytes_out:
group_0 = group[1] | (group[0] << 8)
group_1 = group[3] | (group[2] << 8)
group_2 = group[5] | (group[4] << 8)
group_3 = group[7] | (group[6] << 8)
group_type = (group_1 >> 12) & 0xf # here is what each one means, e.g. RT is radiotext which is the only one we decode here: ["BASIC", "PIN/SL", "RT", "AID", "CT", "TDC", "IH", "RP", "TMC", "EWS", "___", "___", "___", "___", "EON", "___"]
AB = (group_1 >> 11 ) & 0x1 # b if 1, a if 0
#print("group_type:", group_type) # this is essentially message type, i only see type 0 and 2 in my recording
#print("AB:", AB)
program_identification = group_0 # "PI"
program_type = (group_1 >> 5) & 0x1f # "PTY"
pty = pty_table[program_type][pty_locale]
pi_area_coverage = (program_identification >> 8) & 0xf
coverage_area = coverage_area_codes[pi_area_coverage]
pi_program_reference_number = program_identification & 0xff # just an int
if first_time:
print("PTY:", pty)
print("program:", pi_program_reference_number)
print("coverage_area:", coverage_area)
first_time = False
if group_type == 2:
# when the A/B flag is toggled, flush your current radiotext
if radiotext_AB_flag != ((group_1 >> 4) & 0x01):
radiotext = [' ']*65
radiotext_AB_flag = (group_1 >> 4) & 0x01
text_segment_address_code = group_1 & 0x0f
if AB:
radiotext[text_segment_address_code * 2 ] = chr((group_3 >> 8) & 0xff)
radiotext[text_segment_address_code * 2 + 1] = chr(group_3 & 0xff)
else:
radiotext[text_segment_address_code *4 ] = chr((group_2 >> 8) & 0xff)
radiotext[text_segment_address_code * 4 + 1] = chr(group_2 & 0xff)
radiotext[text_segment_address_code * 4 + 2] = chr((group_3 >> 8) & 0xff)
radiotext[text_segment_address_code * 4 + 3] = chr(group_3 & 0xff)
print(''.join(radiotext))
else:
pass
#print("unsupported group_type:", group_type)
A continuación se muestra el resultado del paso de análisis para una estación de FM de ejemplo. Observe cómo tiene que construir la cadena de radiotexto sobre múltiples mensajes, y luego periódicamente borra la cadena y comienza de nuevo. Si está utilizando el archivo descargado de 1 millon de muestras, solo verá las primeras líneas a continuación.
PTY: Top 40
program: 29
coverage_area: Regional 4
ing.
ing. Upb
ing. Upbeat.
ing. Upbeat. Rea
WAY-
WAY-FM U
WAY-FM Uplif
WAY-FM Uplifting
WAY-FM Uplifting. Up
WAY-FM Uplifting. Upbeat
WAY-FM Uplifting. Upbeat. Re
WayF
WayFM Up
WayFM Uplift
WayFM Uplifting.
WayFM Uplifting. Upb
WayFM Uplifting. Upbeat.
WayFM Uplifting. Upbeat. Rea
Resumen y código final¶
¡Lo hiciste! A continuación se muestra todo el código anterior, concatenado, debería funcionar con la prueba de grabación de radio FM que puedes encontrar aquí, aunque debería poder transmitir su propia señal siempre que se reciba con una SNR lo suficientemente alta, simplemente sintonice la frecuencia central de la estación y muestree a una velocidad de 250 kHz. Si descubre que tuvo que hacer ajustes para que funcione con su propia grabación o SDR en vivo, hágame saber lo que tuvo que hacer; puede enviarlo como Pull Request (PR) de GitHub en la página de GitHub del libro de texto. También puede encontrar una versión de este código con docenas de graficas/impresión de depuración incluidos, que utilicé originalmente para hacer este capítulo. aqui.
Final Code
import numpy as np
from scipy.signal import resample_poly, firwin, bilinear, lfilter
import matplotlib.pyplot as plt
# Read in signal
x = np.fromfile('/home/marc/Downloads/fm_rds_250k_from_sdrplay.iq', dtype=np.complex64)
sample_rate = 250e3
center_freq = 99.5e6
# Quadrature Demod
x = 0.5 * np.angle(x[0:-1] * np.conj(x[1:])) # see https://wiki.gnuradio.org/index.php/Quadrature_Demod
# Freq shift
N = len(x)
f_o = -57e3 # amount we need to shift by
t = np.arange(N)/sample_rate # time vector
x = x * np.exp(2j*np.pi*f_o*t) # down shift
# Low-Pass Filter
taps = firwin(numtaps=101, cutoff=7.5e3, fs=sample_rate)
x = np.convolve(x, taps, 'valid')
# Decimate by 10, now that we filtered and there wont be aliasing
x = x[::10]
sample_rate = 25e3
# Resample to 19kHz
x = resample_poly(x, 19, 25) # up, down
sample_rate = 19e3
# Symbol sync, using what we did in sync chapter
samples = x # for the sake of matching the sync chapter
samples_interpolated = resample_poly(samples, 32, 1) # we'll use 32 as the interpolation factor, arbitrarily chosen
sps = 16
mu = 0.01 # initial estimate of phase of sample
out = np.zeros(len(samples) + 10, dtype=np.complex64)
out_rail = np.zeros(len(samples) + 10, dtype=np.complex64) # stores values, each iteration we need the previous 2 values plus current value
i_in = 0 # input samples index
i_out = 2 # output index (let first two outputs be 0)
while i_out < len(samples) and i_in+32 < len(samples):
out[i_out] = samples_interpolated[i_in*32 + int(mu*32)] # grab what we think is the "best" sample
out_rail[i_out] = int(np.real(out[i_out]) > 0) + 1j*int(np.imag(out[i_out]) > 0)
x = (out_rail[i_out] - out_rail[i_out-2]) * np.conj(out[i_out-1])
y = (out[i_out] - out[i_out-2]) * np.conj(out_rail[i_out-1])
mm_val = np.real(y - x)
mu += sps + 0.01*mm_val
i_in += int(np.floor(mu)) # round down to nearest int since we are using it as an index
mu = mu - np.floor(mu) # remove the integer part of mu
i_out += 1 # increment output index
x = out[2:i_out] # remove the first two, and anything after i_out (that was never filled out)
#new sample_rate should be 1187.5
sample_rate /= 16
# Fine freq sync
samples = x # for the sake of matching the sync chapter
N = len(samples)
phase = 0
freq = 0
# These next two params is what to adjust, to make the feedback loop faster or slower (which impacts stability)
alpha = 8.0
beta = 0.002
out = np.zeros(N, dtype=np.complex64)
freq_log = []
for i in range(N):
out[i] = samples[i] * np.exp(-1j*phase) # adjust the input sample by the inverse of the estimated phase offset
error = np.real(out[i]) * np.imag(out[i]) # This is the error formula for 2nd order Costas Loop (e.g. for BPSK)
# Advance the loop (recalc phase and freq offset)
freq += (beta * error)
freq_log.append(freq * sample_rate / (2*np.pi)) # convert from angular velocity to Hz for logging
phase += freq + (alpha * error)
# Optional: Adjust phase so its always between 0 and 2pi, recall that phase wraps around every 2pi
while phase >= 2*np.pi:
phase -= 2*np.pi
while phase < 0:
phase += 2*np.pi
x = out
# Demod BPSK
bits = (np.real(x) > 0).astype(int) # 1's and 0's
# Differential decoding, so that it doesn't matter whether our BPSK was 180 degrees rotated without us realizing it
bits = (bits[1:] - bits[0:-1]) % 2
bits = bits.astype(np.uint8) # for decoder
###########
# DECODER #
###########
# Constants
syndrome = [383, 14, 303, 663, 748]
offset_pos = [0, 1, 2, 3, 2]
offset_word = [252, 408, 360, 436, 848]
# see Annex B, page 64 of the standard
def calc_syndrome(x, mlen):
reg = 0
plen = 10
for ii in range(mlen, 0, -1):
reg = (reg << 1) | ((x >> (ii-1)) & 0x01)
if (reg & (1 << plen)):
reg = reg ^ 0x5B9
for ii in range(plen, 0, -1):
reg = reg << 1
if (reg & (1 << plen)):
reg = reg ^ 0x5B9
return reg & ((1 << plen) - 1) # select the bottom plen bits of reg
# Initialize all the working vars we'll need during the loop
synced = False
presync = False
wrong_blocks_counter = 0
blocks_counter = 0
group_good_blocks_counter = 0
reg = np.uint32(0) # was unsigned long in C++ (64 bits) but numpy doesn't support bitwise ops of uint64, I don't think it gets that high anyway
lastseen_offset_counter = 0
lastseen_offset = 0
# the synchronization process is described in Annex C, page 66 of the standard */
bytes_out = []
for i in range(len(bits)):
# in C++ reg doesn't get init so it will be random at first, for ours its 0s
# It was also an unsigned long but never seemed to get anywhere near the max value
# bits are either 0 or 1
reg = np.bitwise_or(np.left_shift(reg, 1), bits[i]) # reg contains the last 26 rds bits. these are both bitwise ops
if not synced:
reg_syndrome = calc_syndrome(reg, 26)
for j in range(5):
if reg_syndrome == syndrome[j]:
if not presync:
lastseen_offset = j
lastseen_offset_counter = i
presync = True
else:
if offset_pos[lastseen_offset] >= offset_pos[j]:
block_distance = offset_pos[j] + 4 - offset_pos[lastseen_offset]
else:
block_distance = offset_pos[j] - offset_pos[lastseen_offset]
if (block_distance*26) != (i - lastseen_offset_counter):
presync = False
else:
print('Sync State Detected')
wrong_blocks_counter = 0
blocks_counter = 0
block_bit_counter = 0
block_number = (j + 1) % 4
group_assembly_started = False
synced = True
break # syndrome found, no more cycles
else: # SYNCED
# wait until 26 bits enter the buffer */
if block_bit_counter < 25:
block_bit_counter += 1
else:
good_block = False
dataword = (reg >> 10) & 0xffff
block_calculated_crc = calc_syndrome(dataword, 16)
checkword = reg & 0x3ff
if block_number == 2: # manage special case of C or C' offset word
block_received_crc = checkword ^ offset_word[block_number]
if (block_received_crc == block_calculated_crc):
good_block = True
else:
block_received_crc = checkword ^ offset_word[4]
if (block_received_crc == block_calculated_crc):
good_block = True
else:
wrong_blocks_counter += 1
good_block = False
else:
block_received_crc = checkword ^ offset_word[block_number] # bitwise xor
if block_received_crc == block_calculated_crc:
good_block = True
else:
wrong_blocks_counter += 1
good_block = False
# Done checking CRC
if block_number == 0 and good_block:
group_assembly_started = True
group_good_blocks_counter = 1
group = bytearray(8) # 8 bytes filled with 0s
if group_assembly_started:
if not good_block:
group_assembly_started = False
else:
# raw data bytes, as received from RDS. 8 info bytes, followed by 4 RDS offset chars: ABCD/ABcD/EEEE (in US) which we leave out here
# RDS information words
# block_number is either 0,1,2,3 so this is how we fill out the 8 bytes
group[block_number*2] = (dataword >> 8) & 255
group[block_number*2+1] = dataword & 255
group_good_blocks_counter += 1
#print('group_good_blocks_counter:', group_good_blocks_counter)
if group_good_blocks_counter == 5:
#print(group)
bytes_out.append(group) # list of len-8 lists of bytes
block_bit_counter = 0
block_number = (block_number + 1) % 4
blocks_counter += 1
if blocks_counter == 50:
if wrong_blocks_counter > 35: # This many wrong blocks must mean we lost sync
print("Lost Sync (Got ", wrong_blocks_counter, " bad blocks on ", blocks_counter, " total)")
synced = False
presync = False
else:
print("Still Sync-ed (Got ", wrong_blocks_counter, " bad blocks on ", blocks_counter, " total)")
blocks_counter = 0
wrong_blocks_counter = 0
###########
# PARSER #
###########
# Annex F of RBDS Standard Table F.1 (North America) and Table F.2 (Europe)
# Europe North America
pty_table = [["Undefined", "Undefined"],
["News", "News"],
["Current Affairs", "Information"],
["Information", "Sports"],
["Sport", "Talk"],
["Education", "Rock"],
["Drama", "Classic Rock"],
["Culture", "Adult Hits"],
["Science", "Soft Rock"],
["Varied", "Top 40"],
["Pop Music", "Country"],
["Rock Music", "Oldies"],
["Easy Listening", "Soft"],
["Light Classical", "Nostalgia"],
["Serious Classical", "Jazz"],
["Other Music", "Classical"],
["Weather", "Rhythm & Blues"],
["Finance", "Soft Rhythm & Blues"],
["Children’s Programmes", "Language"],
["Social Affairs", "Religious Music"],
["Religion", "Religious Talk"],
["Phone-In", "Personality"],
["Travel", "Public"],
["Leisure", "College"],
["Jazz Music", "Spanish Talk"],
["Country Music", "Spanish Music"],
["National Music", "Hip Hop"],
["Oldies Music", "Unassigned"],
["Folk Music", "Unassigned"],
["Documentary", "Weather"],
["Alarm Test", "Emergency Test"],
["Alarm", "Emergency"]]
pty_locale = 1 # set to 0 for Europe which will use first column instead
# page 72, Annex D, table D.2 in the standard
coverage_area_codes = ["Local",
"International",
"National",
"Supra-regional",
"Regional 1",
"Regional 2",
"Regional 3",
"Regional 4",
"Regional 5",
"Regional 6",
"Regional 7",
"Regional 8",
"Regional 9",
"Regional 10",
"Regional 11",
"Regional 12"]
radiotext_AB_flag = 0
radiotext = [' ']*65
first_time = True
for group in bytes_out:
group_0 = group[1] | (group[0] << 8)
group_1 = group[3] | (group[2] << 8)
group_2 = group[5] | (group[4] << 8)
group_3 = group[7] | (group[6] << 8)
group_type = (group_1 >> 12) & 0xf # here is what each one means, e.g. RT is radiotext which is the only one we decode here: ["BASIC", "PIN/SL", "RT", "AID", "CT", "TDC", "IH", "RP", "TMC", "EWS", "___", "___", "___", "___", "EON", "___"]
AB = (group_1 >> 11 ) & 0x1 # b if 1, a if 0
#print("group_type:", group_type) # this is essentially message type, i only see type 0 and 2 in my recording
#print("AB:", AB)
program_identification = group_0 # "PI"
program_type = (group_1 >> 5) & 0x1f # "PTY"
pty = pty_table[program_type][pty_locale]
pi_area_coverage = (program_identification >> 8) & 0xf
coverage_area = coverage_area_codes[pi_area_coverage]
pi_program_reference_number = program_identification & 0xff # just an int
if first_time:
print("PTY:", pty)
print("program:", pi_program_reference_number)
print("coverage_area:", coverage_area)
first_time = False
if group_type == 2:
# when the A/B flag is toggled, flush your current radiotext
if radiotext_AB_flag != ((group_1 >> 4) & 0x01):
radiotext = [' ']*65
radiotext_AB_flag = (group_1 >> 4) & 0x01
text_segment_address_code = group_1 & 0x0f
if AB:
radiotext[text_segment_address_code * 2 ] = chr((group_3 >> 8) & 0xff)
radiotext[text_segment_address_code * 2 + 1] = chr(group_3 & 0xff)
else:
radiotext[text_segment_address_code *4 ] = chr((group_2 >> 8) & 0xff)
radiotext[text_segment_address_code * 4 + 1] = chr(group_2 & 0xff)
radiotext[text_segment_address_code * 4 + 2] = chr((group_3 >> 8) & 0xff)
radiotext[text_segment_address_code * 4 + 3] = chr(group_3 & 0xff)
print(''.join(radiotext))
else:
pass
#print("unsupported group_type:", group_type)
Una vez más, el ejemplo de grabación de FM que funciona con este código lo puede encontra aqui.
Para aquellos interesados en demodular la señal de audio real, simplemente agregue las siguientes líneas justo después de la sección “Adquirir una señal” (agradecimiento especial a Joel Cordeiro por el código):
# Add the following code right after the "Acquiring a Signal" section
from scipy.io import wavfile
# Demodulation
x = np.diff(np.unwrap(np.angle(x)))
# De-emphasis filter, H(s) = 1/(RC*s + 1), implemented as IIR via bilinear transform
bz, az = bilinear(1, [75e-6, 1], fs=sample_rate)
x = lfilter(bz, az, x)
# decimate by 6 to get mono audio
x = x[::6]
sample_rate_audio = sample_rate/6
# normalize volume so its between -1 and +1
x /= np.max(np.abs(x))
# some machines want int16s
x *= 32767
x = x.astype(np.int16)
# Save to wav file, you can open this in Audacity for example
wavfile.write('fm.wav', int(sample_rate_audio), x)
La parte más complicada es el filtro de de-emphasis, sobre el cual puedes aprender aquí, aunque en realidad es un paso opcional si estás de acuerdo con el audio que tiene un equilibrio deficiente de graves y agudos. Para aquellos curiosos, aquí está cuál es la respuesta de frecuencia del IIR parece que el filtro de de-emphasis no filtra completamente ninguna frecuencia, es más bien un filtro “formador”.
Agradecimientos GNU Radio¶
La mayoría de los pasos anteriores utilizados para recibir RDS se adaptaron de la implementación de RDS de GNU Radio, que se encuentra en el módulo fuera del árbol de GNU Radio llamado gr-rds, creado originalmente por Dimitrios Symeonidis y mantenido por Bastian Bloessl, y me gustaría reconocer el trabajo de estos autores. Para crear este capítulo, comencé a usar gr-rds en GNU Radio, con una grabación de FM funcional, y poco a poco convertí cada uno de los bloques (incluidos muchos bloques integrados) a Python. Tomó bastante tiempo, hay algunos matices en los bloques integrados que son fáciles de pasar por alto, y pasar del procesamiento del formato de la señal (es decir, usar una función de trabajo que procesa unos pocos miles de muestras a la vez en un manera estable) a un bloque de Python no siempre es sencillo. GNU Radio es una herramienta increíble para este tipo de creación de prototipos y nunca habría podido crear todo este código Python funcional sin ella.
