15. Formador de Pulso¶

Este capítulo cubre la conformación de pulsos, la interferencia entre símbolos, el filtrado coincidente y los filtros de coseno elevado. Al final usamos Python para agregar configuración de pulso a los símbolos BPSK. Puede considerar esta sección, Parte II del capítulo Filtros, donde profundizamos en la configuración del pulso.

Interferencia entre simbolos (ISI)¶

En el capitulo Filtros aprendimos que los símbolos/pulsos en forma de bloques utilizan una cantidad excesiva de espectro, y podemos reducir en gran medida la cantidad de espectro utilizado “dando forma” a nuestros pulsos. Sin embargo, no puedes usar cualquier filtro de paso bajo o podrías obtener interferencia entre símbolos (ISI), donde los símbolos se fusionan e interfieren entre sí.

Cuando transmitimos símbolos digitales, los transmitimos uno tras otro (en lugar de esperar un tiempo entre ellos). Cuando se aplica un filtro de configuración de pulso, se alarga el pulso en el dominio del tiempo (para condensarlo en frecuencia), lo que hace que los símbolos adyacentes se superpongan entre sí. La superposición está bien, siempre y cuando su filtro de configuración de pulsos cumpla con este criterio: todos los pulsos deben sumar cero en cada múltiplo de nuestro período de símbolo. $T$ , excepto uno de los pulsos. La idea se comprende mejor a través de la siguiente visualización:

Como puedes ver en cada intervalo de $T$ , hay un pico de pulso mientras que el resto de los pulsos están en 0 (cruzan el eje x). Cuando el receptor muestrea la señal, lo hace en el momento perfecto (en el pico de los pulsos), lo que significa que ese es el único momento que importa. Generalmente hay un bloque de sincronización de símbolos en el receptor que garantiza que los símbolos se muestreen en los picos.

Filtro acoplado¶

Un truco que utilizamos en las comunicaciones inalámbricas se llama filtrado coincidente. Para comprender el filtrado coincidente, primero debe comprender estos dos puntos:

Los pulsos que comentamos anteriormente sólo tienen que estar perfectamente alineados en el receptor antes del muestreo. Hasta ese momento, realmente no importa si hay ISI, es decir, las señales pueden volar por el aire con ISI y está bien.
Queremos un filtro paso bajo en nuestro transmisor para reducir la cantidad de espectro que utiliza nuestra señal. Pero el receptor también necesita un filtro de paso bajo para eliminar la mayor cantidad posible de ruido/interferencia junto a la señal. Como resultado, tenemos un filtro paso bajo en el transmisor (Tx) y otro en el receptor (Rx), luego el muestreo ocurre después de ambos filtros (y los efectos del canal inalámbrico).

Lo que hacemos en las comunicaciones modernas es dividir el filtro formador de pulsos en partes iguales entre Tx y Rx. No tienen que ser filtros idénticos, pero, teóricamente, el filtro lineal óptimo para maximizar la SNR en presencia de AWGN es usar el mismo filtro tanto en Tx como en Rx. Esta estrategia se denomina como el concepto del “filtro acoplado”.

Otra forma de pensar en los filtros acoplados es que el receptor correlaciona la señal recibida con la señal plantilla conocida. La señal de plantilla son esencialmente los pulsos que envía el transmisor, independientemente de los cambios de fase/amplitud que se les apliquen. Recuerde que el filtrado se realiza mediante convolución, que es básicamente correlación (de hecho, son matemáticamente iguales cuando la plantilla es simétrica). Este proceso de correlacionar la señal recibida con la plantilla nos brinda la mejor oportunidad de recuperar lo que se envió y es por eso que es teóricamente óptimo. Como analogía, piense en un sistema de reconocimiento de imágenes que busca caras utilizando una plantilla de cara y una correlación 2D:

Dividir un filtro por la mitad¶

¿Cómo dividimos realmente un filtro por la mitad? La convolución es asociativa, lo que significa:

$(f * g) * h = f * (g * h)$

Imaginemos $f$ como nuestra señal de entrada, y $g$ y $h$ son filtros. Filtrar $f$ con $g$ , y luego $h$ es lo mismo que filtrar con un filtro igual a $g * h$ .

Además, recuerde que la convolución en el dominio del tiempo es una multiplicación en el dominio de la frecuencia:

$g(t) * h(t) \leftrightarrow G(f)H(f)$

Para dividir un filtro por la mitad, puedes tomar la raíz cuadrada de la respuesta de frecuencia.

$X(f) = X_H(f) X_H(f) \quad \mathrm{where} \quad X_H(f) = \sqrt{X(f)}$

A continuación se muestra un diagrama simplificado de una cadena de transmisión y recepción, con un filtro de coseno elevado (RC) dividido en dos filtros de coseno elevado (RRC); el del lado de transmisión es el filtro formador de pulsos y el del lado de recepción es el filtro acoplado. Juntos, hacen que los pulsos en el demodulador parezcan como si hubieran sido moldeados con un solo filtro RRC.

A diagram of a transmit and receive chain, with a Raised Cosine (RC) filter being split into two Root Raised Cosine (RRC) filters

Filtros Formadores de Pulso Específicos¶

Sabemos que queremos:

Diseñe un filtro que reduzca el ancho de banda de nuestra señal (para usar menos espectro) y todos los pulsos excepto uno deben sumar cero en cada intervalo de símbolo.
Divida el filtro por la mitad, poniendo una mitad en el Tx y la otra en el Rx.

Veamos algunos filtros específicos que se usan comúnmente para dar forma al pulso.

Filtro de Coseno-Elevado¶

El filtro formador de pulsos más popular parece ser el filtro de “coseno elevado”. Es un buen filtro paso bajo para limitar el ancho de banda que ocupará nuestra señal, y además tiene la propiedad de sumar cero en intervalos de $T$ :

The raised cosine filter in the time domain with a variety of roll-off values

Tenga en cuenta que el gráfico anterior está en el dominio del tiempo. Representa la respuesta al impulso del filtro. El parámetro $\beta$ es el único parámetro para el filtro de coseno elevado y determina qué tan rápido el filtro disminuye en el dominio del tiempo, que será inversamente proporcional a la rapidez con la que disminuye en frecuencia:

The raised cosine filter in the frequency domain with a variety of roll-off values

La razón por la que se llama filtro de coseno elevado es porque el dominio de la frecuencia cuando $\beta = 1$ es medio ciclo de la onda coseno, elevada para sentarse en el eje x.

La ecuación que define la respuesta impulsiva del filtro de coseno elevado es:

$h(t) = \frac{1}{T} \mathrm{sinc}\left( \frac{t}{T} \right) \frac{\cos\left(\frac{\pi\beta t}{T}\right)}{1 - \left( \frac{2 \beta t}{T} \right)^2}$

Más información sobre la función $\mathrm{sinc}()$ puedes encontrarla aqui.

Recuerde: dividimos este filtro entre Tx y Rx por igual. ¡Iniciemos con el filtro raíz de coseno elevado (RRC)!

Filtro de la raíz del coseno elevado¶

El filtro raíz de coseno elevado (RRC) es lo que realmente implementamos en nuestros Tx y Rx. Combinados forman un filtro de coseno elevado normal, como comentamos. Debido a que dividir un filtro por la mitad implica una raíz cuadrada en el dominio de la frecuencia, la respuesta al impulso se vuelve un poco confusa:

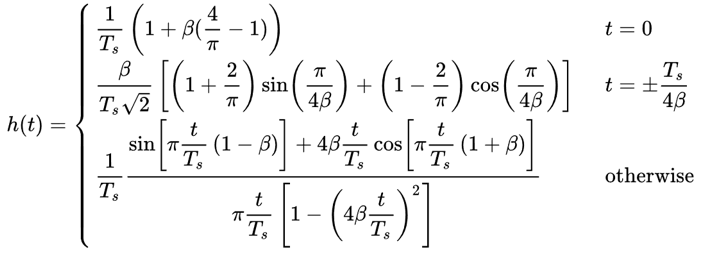
Afortunadamente, es un filtro muy utilizado y existen muchas implementaciones, incluidas en Python.

Otros filtros formadores de pulsos¶

Otros filtros incluyen el filtro gaussiano, que tiene una respuesta de impulso que se asemeja a una función gaussiana. También hay un filtro sinc, que es equivalente al filtro de coseno elevado cuando $\beta = 0$ . El filtro sinc es más bien un filtro ideal, lo que significa que elimina las frecuencias necesarias sin mucha región de transición.

Factor de Roll-Off¶

Analicemos el parámetro $\beta$ . Es un número entre 0 y 1 y se denomina factor de “roll-off” o, a veces, “exceso de ancho de banda”. Determina qué tan rápido, en el dominio del tiempo, el filtro llega a cero. Recuerde que, para usarse como filtro, la respuesta al impulso debe decaer a cero en ambos lados:

Plot of the raised cosine roll-off parameter

Se requieren más taps del filtro, cuanto más bajo sea $\beta$ . Cuando $\beta = 0$ la respuesta al impulso nunca llega completamente a cero, por lo que intentamos que $\beta$ sea lo más bajo posible sin causar otros problemas. Cuanto menor sea la caída, más compacta en frecuencia podremos crear nuestra señal para una velocidad de símbolo determinada, lo cual siempre es importante.

Una ecuación común utilizada para aproximar el ancho de banda, en Hz, para una velocidad de símbolo y un factor de caída determinados es:

$\mathrm{BW} = R_S(\beta + 1)$

$R_S$ es la velocidad de símbolo en Hz. Para las comunicaciones inalámbricas normalmente nos gusta una caída entre 0,2 y 0,5. Como regla general, una señal digital que utiliza velocidad de símbolo $R_S$ ocupará un poco más que $R_S$ de espectro, incluidas las porciones positivas y negativas del espectro. Una vez que convertimos y transmitimos nuestra señal, ambas partes ciertamente importan. Si transmitimos QPSK a 1 millón de símbolos por segundo (MSps), ocupará alrededor de 1,3 MHz. La velocidad de datos será de 2 Mbps (recuerde que QPSK usa 2 bits por símbolo), incluida cualquier sobrecarga como codificación de canal y encabezados de trama.

Ejercicio en Python¶

Como ejercicio de Python, filtremos y demos forma a algunos pulsos. Usaremos símbolos BPSK para que sea más fácil de visualizar; antes del paso de configuración del pulso, BPSK implica transmitir 1 o -1 con la porción “Q” igual a cero. Con Q igual a cero podemos trazar sólo la porción I, y es más fácil de observar.

En esta simulación usaremos 8 muestras por símbolo, y en lugar de usar una señal de onda cuadrada de 1 y -1, usamos un tren de impulsos. Cuando pasas un impulso a través de un filtro, la salida es la respuesta al impulso (de ahí el nombre). Por lo tanto, si desea una serie de pulsos, deberá utilizar impulsos con ceros entre ellos para evitar pulsos cuadrados.

import numpy as np
import matplotlib.pyplot as plt
from scipy import signal

num_symbols = 10
sps = 8

bits = np.random.randint(0, 2, num_symbols) # Our data to be transmitted, 1's and 0's

x = np.array([])
for bit in bits:
    pulse = np.zeros(sps)
    pulse[0] = bit*2-1 # set the first value to either a 1 or -1
    x = np.concatenate((x, pulse)) # add the 8 samples to the signal
plt.figure(0)
plt.plot(x, '.-')
plt.grid(True)
plt.show()

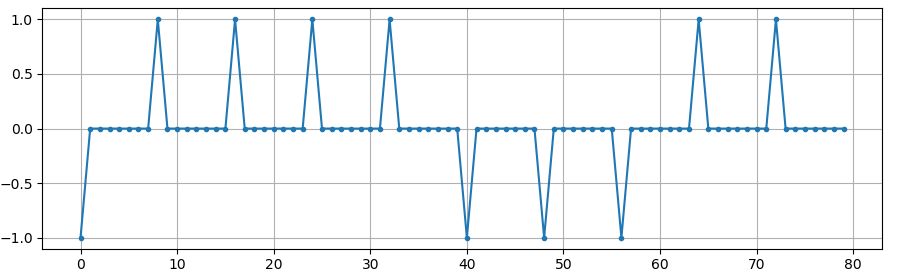
A pulse train of impulses in the time domain simulated in Python

En este punto nuestros símbolos siguen siendo 1 y -1. No se deje atrapar por el hecho de que usamos impulsos. De hecho, podría ser más fácil no visualizar la respuesta de los impulsos, sino pensar en ella como una matriz:

bits: [0, 1, 1, 1, 1, 0, 0, 0, 1, 1]
BPSK symbols: [-1, 1, 1, 1, 1, -1, -1, -1, 1, 1]
Applying 8 samples per symbol: [-1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, ...]

Crearemos un filtro de coseno elevado usando un $\beta$ de 0.35, y lo haremos de 101 taps de largo para darle a la señal suficiente tiempo para decaer a cero. Si bien la ecuación del coseno elevado solicita nuestro período de símbolo y un vector de tiempo $t$ , podemos asumir un período de muestra de 1 segundo para “normalizar” nuestra simulación. Significa que nuestro período de símbolo $Ts$ es 8 porque tenemos 8 muestras por símbolo. Nuestro vector de tiempo será entonces una lista de números enteros. Dada la forma en que funciona la ecuación del coseno elevado, queremos que $t=0$ esté en el centro. Generaremos el vector de tiempo de 101 longitudes comenzando en -51 y terminando en +51.

# Create our raised-cosine filter
num_taps = 101
beta = 0.35
Ts = sps # Assume sample rate is 1 Hz, so sample period is 1, so *symbol* period is 8
t = np.arange(num_taps) - (num_taps-1)//2
h = np.sinc(t/Ts) * np.cos(np.pi*beta*t/Ts) / (1 - (2*beta*t/Ts)**2)
plt.figure(1)
plt.plot(t, h, '.')
plt.grid(True)
plt.show()

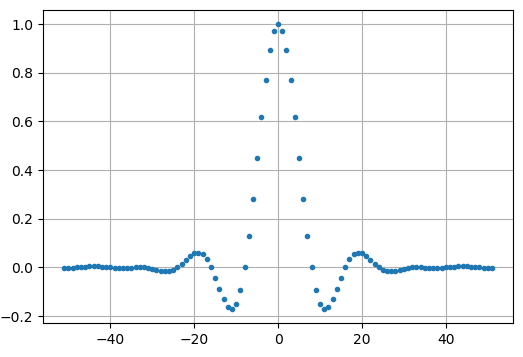
Observe cómo la salida definitivamente decae a cero. El hecho de que estemos usando 8 muestras por símbolo determina qué tan estrecho aparece este filtro y qué tan rápido decae hasta cero. La respuesta de impulso anterior parece un filtro paso bajo típico, y realmente no hay forma de que sepamos si es un filtro formador de pulsos especifico versus cualquier otro filtro paso bajo.

Por último, podemos filtrar nuestra señal $x$ y examinar el resultado. No se concentre demasiado en la introducción de un bucle for en el código proporcionado. Discutiremos por qué está ahí después del bloque de código.

# Filter our signal, in order to apply the pulse shaping
x_shaped = np.convolve(x, h)
plt.figure(2)
plt.plot(x_shaped, '.-')
for i in range(num_symbols):
    plt.plot([i*sps+num_taps//2,i*sps+num_taps//2], [0, x_shaped[i*sps+num_taps//2]])
plt.grid(True)
plt.show()

Esta señal resultante se suma a muchas de nuestras respuestas impulsivas, y aproximadamente la mitad de ellas se multiplica primero por -1. Puede parecer complicado, pero lo superaremos juntos.

En primer lugar, hay muestras transitorias antes y después de los datos debido al filtro y a la forma en que funciona la convolución. Estas muestras adicionales se incluyen en nuestra transmisión pero en realidad no contienen “picos”.

En segundo lugar, las líneas verticales se crearon en el bucle for por motivos de visualización. Están destinados a demostrar dónde ocurren los intervalos de $Ts$ . Estos intervalos representan dónde el receptor muestreará esta señal. Observe que para intervalos de $Ts$ la curva tiene el valor de exactamente 1,0 o -1,0, lo que los convierte en los puntos ideales en el tiempo para muestrear.

Si tuviéramos que convertir y transmitir esta señal, el receptor tendría que determinar cuándo están los límites de $Ts$ , por ejemplo, usando un algoritmo de sincronización de símbolos. De esa manera, el receptor sabe exactamente cuándo tomar muestras para obtener los datos correctos. Si el receptor toma muestras demasiado pronto o demasiado tarde, verá valores que están ligeramente sesgados debido al ISI, y si está muy alejado, obtendrá un montón de números extraños.

Aquí hay un ejemplo, creado con GNU Radio, que ilustra cómo se ve el gráfico IQ (también conocido como constelación) cuando tomamos muestras en los momentos correctos e incorrectos. Los pulsos originales tienen sus valores de bits anotados.

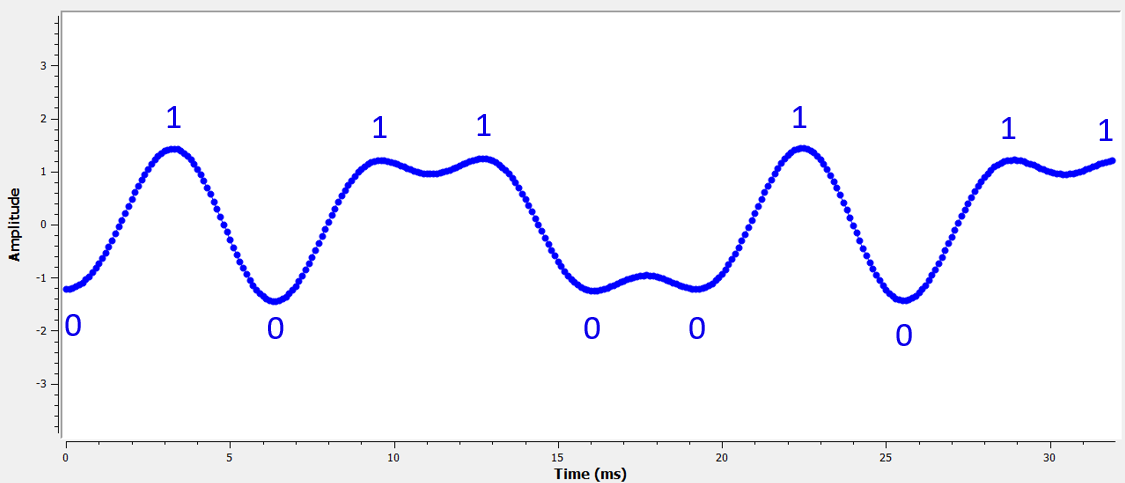
El siguiente gráfico representa la posición ideal en el tiempo para tomar la muestra, junto con el gráfico de IQ:

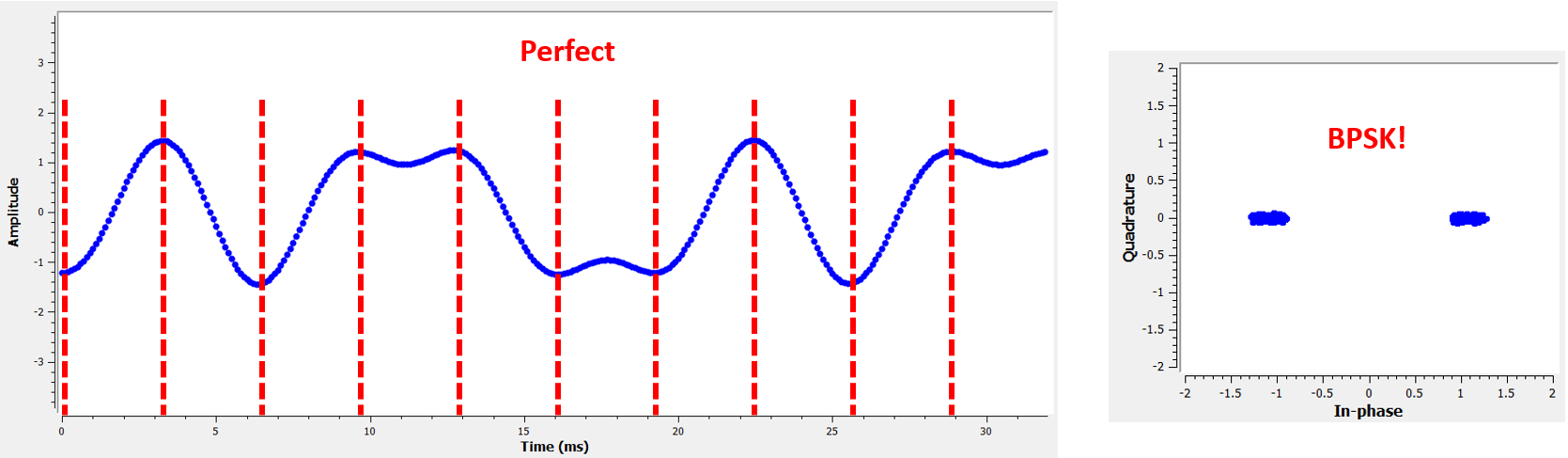
GNU Radio simulation showing perfect sampling as far as timing

Compare eso con el peor momento para tomar muestras. Observe los tres grupos de la constelación. Estamos probando directamente entre cada símbolo; nuestras muestras van a estar muy alejadas.

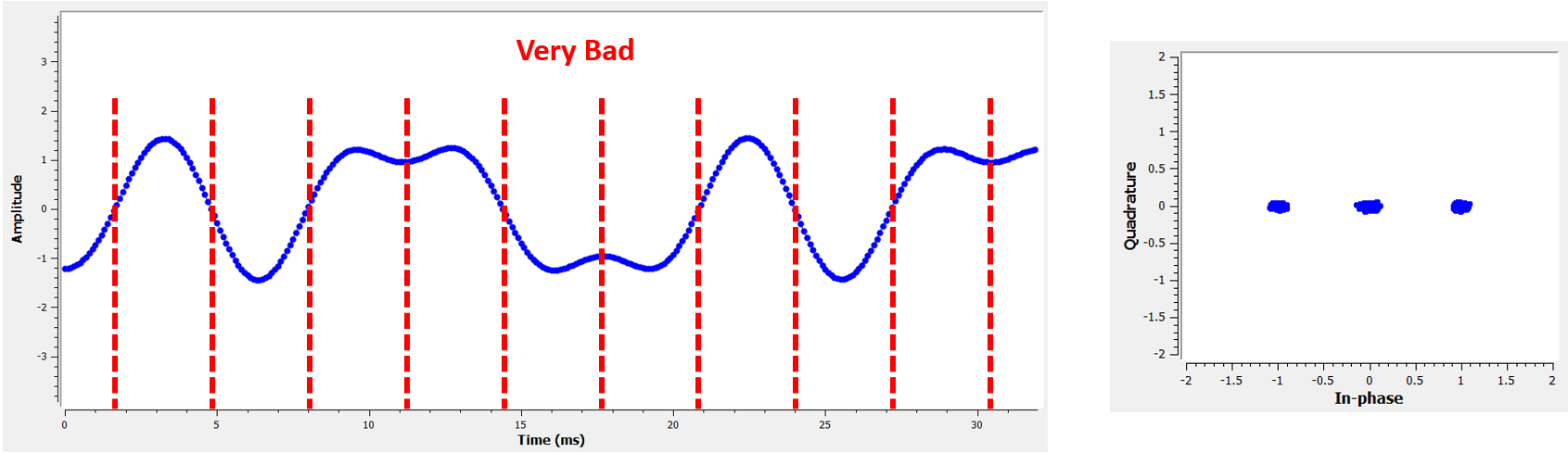
GNU Radio simulation showing imperfect sampling as far as timing

Aquí hay otro ejemplo de un tiempo de muestra deficiente, en algún lugar entre nuestro caso ideal y el peor. Presta atención a los cuatro grupos. Con una SNR alta podríamos salirnos con la nuestra con este intervalo de tiempo de muestreo, aunque no es aconsejable.

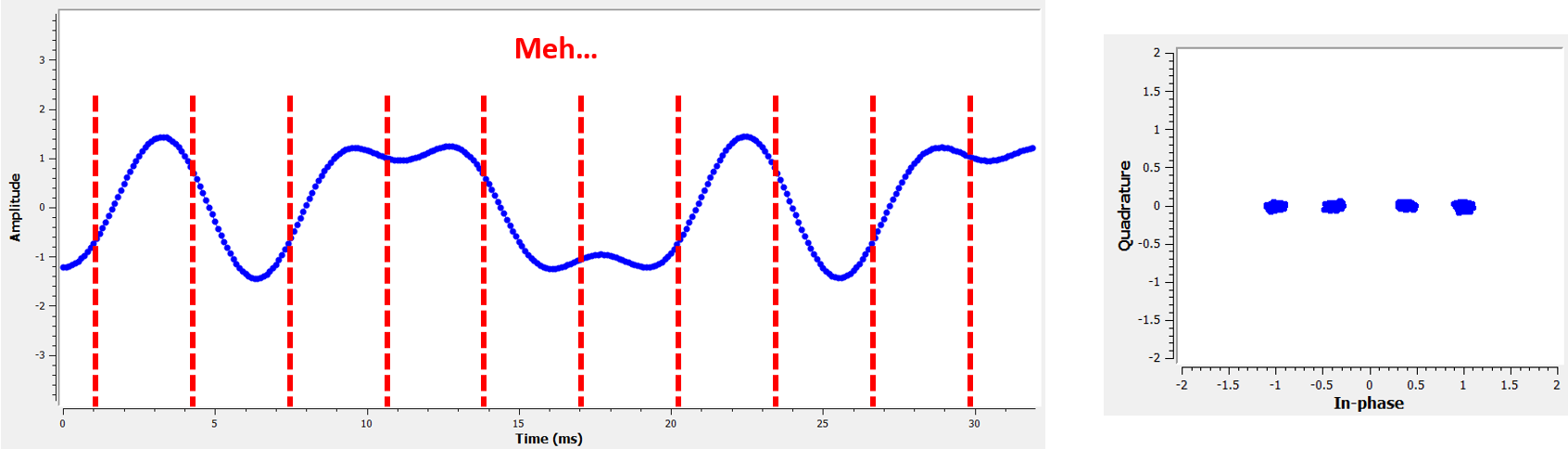
Recuerde que nuestros valores de Q no se muestran en el gráfico del dominio del tiempo porque son aproximadamente cero, lo que permite que los gráficos de IQ se extiendan solo horizontalmente.