16. Sincronización¶

Este capítulo cubre la sincronización de señales inalámbricas tanto en tiempo como en frecuencia, para corregir los desplazamientos de frecuencia de la portadora y realizar la alineación de tiempos a nivel de símbolo y cuadro. Utilizaremos la técnica de recuperación de reloj de Mueller y Muller, y el Costas Loop, en Python.

Introducción a la sincronización¶

Hemos discutido cómo transmitir digitalmente por aire, utilizando un esquema de modulación digital como QPSK y aplicando configuración de pulso para limitar el ancho de banda de la señal. La codificación de canales se puede utilizar para tratar canales ruidosos, como cuando la SNR del receptor es baja. Filtrar tanto como sea posible antes de procesar digitalmente la señal siempre ayuda. En este capítulo investigaremos cómo se realiza la sincronización en el extremo receptor. La sincronización es un conjunto de procesamiento que ocurre antes de la demodulación y decodificación del canal. La cadena tx-channel-rx general se muestra a continuación, con los bloques analizados en este capítulo resaltados en amarillo. (Este diagrama no lo abarca todo; la mayoría de los sistemas también incluyen ecualización y multiplexación).

The transmit receive chain, with the blocks discussed in this chapter highlighted in yellow, including time and frequency synchronization

Simulación de canal inalámbrico¶

Antes de aprender cómo implementar la sincronización de tiempo y frecuencia, debemos hacer que nuestras señales simuladas sean más realistas. Sin agregar algún retraso de tiempo aleatorio, el acto de sincronizar en el tiempo es trivial. De hecho, sólo necesita tener en cuenta el retraso de la muestra de cualquier filtro que utilice. También queremos simular un desplazamiento de frecuencia porque, como veremos, los osciladores no son perfectos; Siempre habrá cierta compensación entre la frecuencia central del transmisor y del receptor.

Examinemos el código Python para simular un retraso no entero y un desplazamiento de frecuencia. El código Python de este capítulo comenzará a partir del código que escribimos durante el ejercicio de Python para dar forma al pulso (haga clic a continuación si lo necesita); puede considerarlo el punto de partida del código de este capítulo, y todo el código nuevo vendrá después.

Python Code from Pulse Shaping

import numpy as np
import matplotlib.pyplot as plt
from scipy import signal
import math

# this part came from pulse shaping exercise
num_symbols = 100
sps = 8
bits = np.random.randint(0, 2, num_symbols) # Our data to be transmitted, 1's and 0's
pulse_train = np.array([])
for bit in bits:
    pulse = np.zeros(sps)
    pulse[0] = bit*2-1 # set the first value to either a 1 or -1
    pulse_train = np.concatenate((pulse_train, pulse)) # add the 8 samples to the signal

# Create our raised-cosine filter
num_taps = 101
beta = 0.35
Ts = sps # Assume sample rate is 1 Hz, so sample period is 1, so *symbol* period is 8
t = np.arange(-51, 52) # remember it's not inclusive of final number
h = np.sinc(t/Ts) * np.cos(np.pi*beta*t/Ts) / (1 - (2*beta*t/Ts)**2)

# Filter our signal, in order to apply the pulse shaping
samples = np.convolve(pulse_train, h)

Dejaremos de lado el código relacionado con el grafico porque probablemente ya haya aprendido a graficar cualquier señal que desee. Hacer que las graficas se vean bonitas, como suele ocurrir en este libro de texto, requiere una gran cantidad de código adicional que no es necesario comprender.

Agregando el retardo¶

Podemos simular fácilmente un retardo desplazando muestras, pero solo simular un retraso que es un múltiplo entero del período de nuestra muestra. En el mundo real, el retardo será de una fracción de un período de muestra. Podemos simular el retardo de una fracción de una muestra creando un filtro de “retardo fraccional”, que pasa todas las frecuencias pero retrasa las muestras en una cantidad que no se limita al intervalo de la muestra. Puedes considerarlo como un filtro de paso total que aplica el mismo cambio de fase a todas las frecuencias. (Recuerde que un retardo de tiempo y un cambio de fase son equivalentes). El código Python para crear este filtro se muestra a continuación:

# Create and apply fractional delay filter
delay = 0.4 # fractional delay, in samples
N = 21 # number of taps
n = np.arange(-N//2, N//2) # ...-3,-2,-1,0,1,2,3...
h = np.sinc(n - delay) # calc filter taps
h *= np.hamming(N) # window the filter to make sure it decays to 0 on both sides
h /= np.sum(h) # normalize to get unity gain, we don't want to change the amplitude/power
samples = np.convolve(samples, h) # apply filter

Como puede ver, estamos calculando los taps del filtro usando una función sinc(). Un sinc en el dominio del tiempo es un rectángulo en el dominio de la frecuencia, y nuestro rectángulo para este filtro abarca todo el rango de frecuencia de nuestra señal. Este filtro no recontruye la señal, simplemente la retrasa en el tiempo. En nuestro ejemplo estamos retrasando 0,4 de una muestra. Tenga en cuenta que la aplicación de cualquier filtro retrasa la señal a la mitad de los taps del filtro menos uno, debido al acto de convolucionar la señal a través del filtro.

Si trazamos el “antes” y el “después” del filtrado de una señal, podemos observar el retraso fraccionario. En nuestra trama nos acercamos sólo a un par de símbolos. De lo contrario, el retraso fraccionario no será visible.

$../_images/fractional-delay-filter.svg$

Agregando desplazamiento en frecuencia¶

Para hacer nuestra señal simulada más realista, aplicaremos un desplazamiento de frecuencia. Digamos que nuestra frecuencia de muestreo en esta simulación es 1 MHz (en realidad no importa cuál sea, pero verás por qué hace que sea más fácil elegir un número). Si queremos simular un desplazamiento de frecuencia de 13 kHz (algún número arbitrario), podemos hacerlo mediante el siguiente código:

# apply a freq offset
fs = 1e6 # assume our sample rate is 1 MHz
fo = 13000 # simulate freq offset
Ts = 1/fs # calc sample period
t = np.arange(0, Ts*len(samples), Ts) # create time vector
samples = samples * np.exp(1j*2*np.pi*fo*t) # perform freq shift

A continuación se muestra la señal antes y después de aplicar el desplazamiento de frecuencia.

Python simulation showing a signal before and after applying a frequency offset

No hemos estado graficando la porción Q desde que transmitimos BPSK, por lo que la porción Q siempre es cero. Ahora que estamos agregando un cambio de frecuencia para simular canales inalámbricos, la energía se distribuye entre I y Q. A partir de este punto deberíamos trazar tanto I como Q. Siéntase libre de sustituir su código por un desplazamiento de frecuencia diferente. Si reduce el desplazamiento a aproximadamente 1 kHz, podrá ver la sinusoide en la envolvente de la señal porque oscila lo suficientemente lenta como para abarcar varios símbolos.

En cuanto a elegir una frecuencia de muestreo arbitraria, si examina el código, notará que lo que importa es la relación entre fo y fs.

Puedes pretender que los dos bloques de código presentados anteriormente simulan un canal inalámbrico. El código debe aparecer después del código del lado de transmisión (lo que hicimos en el capítulo sobre configuración de pulsos) y antes del código del lado de recepción, que es lo que exploraremos en el resto de este capítulo.

Sincronización en tiempo¶

Cuando transmitimos una señal de forma inalámbrica, llega al receptor con un cambio de fase aleatorio debido al tiempo recorrido. No podemos simplemente comenzar a muestrear los símbolos a nuestra velocidad de símbolo porque es poco probable que lo hagamos en el punto correcto del pulso, como se explica al final del capítulo. Formador de Pulso. Revise las tres figuras al final de ese capítulo si no las está siguiendo.

La mayoría de las técnicas de sincronización de tiempo toman la forma de un bucle de bloqueo de fase (PLL); no estudiaremos los PLL aquí, pero es importante conocer el término y, si está interesado, puede leer sobre ellos por su cuenta. Los PLL son sistemas de circuito cerrado que utilizan retroalimentación para ajustar algo continuamente; en nuestro caso, un cambio de tiempo nos permite muestrear en el pico de los símbolos digitales.

Puede imaginarse la recuperación de tiempo como un bloque en el receptor, que acepta un flujo de muestras y genera otro flujo de muestras (similar a un filtro). Programamos este bloque de recuperación de temporización con información sobre nuestra señal, siendo la más importante la cantidad de muestras por símbolo (o nuestra mejor suposición, si no estamos 100% seguros de lo que se transmitió). Este bloque actúa como un “decimador”, es decir, nuestra la muestra de salida será una fracción del número de muestras entrantes. Queremos una muestra por símbolo digital, por lo que la tasa de diezmado es simplemente las muestras por símbolo. Si el transmisor transmite a 1 millón de símbolos por segundo y tomamos muestras a 16 Msps, recibiremos 16 muestras por símbolo. Esa será la frecuencia de muestreo que entrará en el bloque de sincronización de tiempo. La frecuencia de muestreo que sale del bloque será de 1 Msps porque queremos una muestra por símbolo digital.

La mayoría de los métodos de recuperación de tiempo se basan en el hecho de que nuestros símbolos digitales suben y luego bajan, y la cresta es el punto en el que queremos muestrear el símbolo. Para decirlo de otra manera, tomamos una muestra del punto máximo después de tomar el valor absoluto:

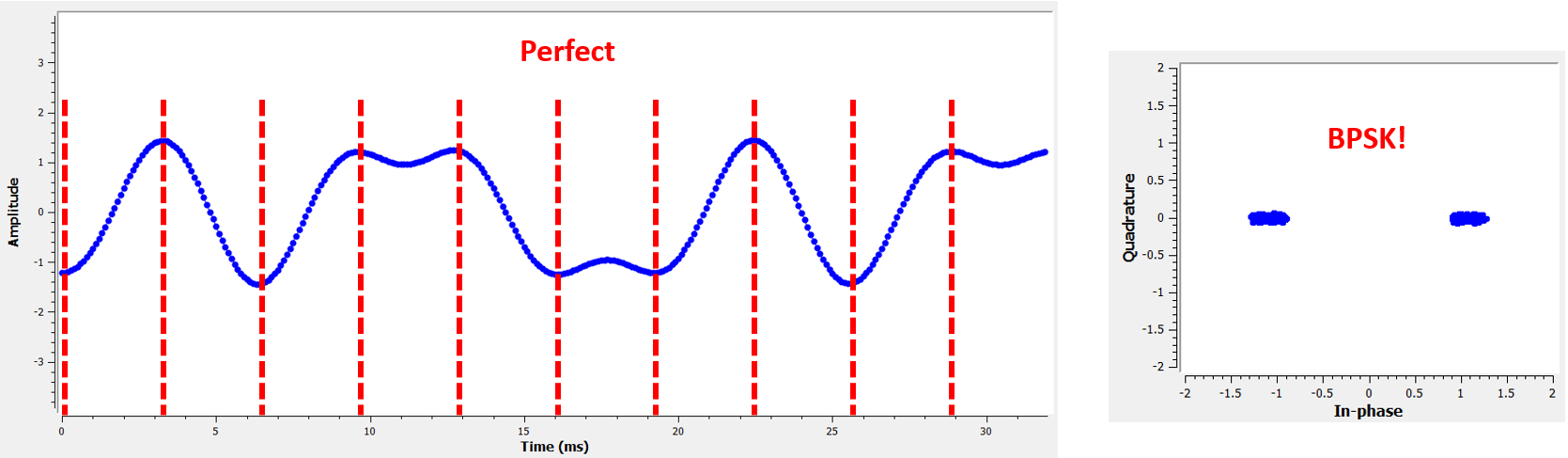
Existen muchos métodos para recuperar la sincronización, la mayoría parecidos a un PLL. Generalmente, la diferencia entre ellos es la ecuación utilizada para realizar la “corrección” en el desplazamiento de tiempo, que denotamos como $\mu$ o mu en el código. El valor de mu se actualiza en cada iteración del bucle. Está en unidades de muestras, y se puede considerar cuánto tenemos que desplazarnos para poder tomar muestras en el momento “perfecto”. Entonces, si mu = 3.61 entonces eso significa que tenemos que cambiar la entrada en 3.61 muestras para muestrear en el lugar correcto. Debido a que tenemos 8 muestras por símbolo, si mu supera 8, simplemente volverá a cero.

El siguiente código Python implementa la técnica de recuperación del reloj de Mueller y Muller.

mu = 0 # initial estimate of phase of sample
out = np.zeros(len(samples) + 10, dtype=np.complex)
out_rail = np.zeros(len(samples) + 10, dtype=np.complex) # stores values, each iteration we need the previous 2 values plus current value
i_in = 0 # input samples index
i_out = 2 # output index (let first two outputs be 0)
while i_out < len(samples) and i_in+16 < len(samples):
    out[i_out] = samples[i_in + int(mu)] # grab what we think is the "best" sample
    out_rail[i_out] = int(np.real(out[i_out]) > 0) + 1j*int(np.imag(out[i_out]) > 0)
    x = (out_rail[i_out] - out_rail[i_out-2]) * np.conj(out[i_out-1])
    y = (out[i_out] - out[i_out-2]) * np.conj(out_rail[i_out-1])
    mm_val = np.real(y - x)
    mu += sps + 0.3*mm_val
    i_in += int(np.floor(mu)) # round down to nearest int since we are using it as an index
    mu = mu - np.floor(mu) # remove the integer part of mu
    i_out += 1 # increment output index
out = out[2:i_out] # remove the first two, and anything after i_out (that was never filled out)
samples = out # only include this line if you want to connect this code snippet with the Costas Loop later on

El bloque de recuperación de temporización “recibe” las muestras y produce una muestra de salida una a la vez (tenga en cuenta que i_out se incrementa en 1 en cada iteración del bucle). El bloque de recuperación no solo usa las muestras “recibidas” una tras otra debido a la forma en que se ajusta el bucle i_in. Saltará algunas muestras en un intento de extraer la muestra “correcta”, que sería la que se encuentra en el pico del pulso. A medida que el bucle procesa muestras, se sincroniza lentamente con el símbolo, o al menos lo intenta ajustando mu. Dada la estructura del código, la parte entera de mu se agrega a i_in y luego se elimina de mu (tenga en cuenta que mm_val puede ser negativo o positivo cada bucle). Una vez que esté completamente sincronizado, el bucle solo debe extraer la muestra central de cada símbolo/pulso. Puede ajustar la constante 0.3 , lo que cambiará la rapidez con la que reacciona el circuito de retroalimentación; un valor más alto hará que reaccione más rápido, pero con mayor riesgo de problemas de estabilidad.

El siguiente gráfico muestra un ejemplo de resultado en el que hemos deshabilitado el retardo de tiempo fraccionario así como el desplazamiento de frecuencia. Solo mostramos I porque Q es todo ceros con el desplazamiento de frecuencia desactivado. Los tres gráficos están apilados uno encima del otro para mostrar cómo se alinean verticalmente los bits.

Grafica superior: Símbolos BPSK originales, es decir, 1 y -1. Recuerde que hay ceros en el medio porque queremos 8 muestras por símbolo.
Grafica intermedia: Muestras después de la conformación del pulso pero antes del sincronizador.
Grafica inferior: Salida del sincronizador de símbolos, que proporciona solo 1 muestra por símbolo. Es decir, estas muestras se pueden alimentar directamente a un demodulador, que para BPSK verifica si el valor es mayor o menor que 0.

Centrémonos en el gráfico inferior, que es la salida del sincronizador. Se necesitaron casi 30 símbolos para que la sincronización se fijara en el retardo correcto. Inevitablemente al tiempo que tardan los sincronizadores en ajustarse; muchos protocolos de comunicaciones utilizan un preámbulo que contiene una secuencia de sincronización: actúa como una forma de anunciar que ha llegado un nuevo paquete y le da tiempo al receptor para sincronizarse con él. Pero después de estas ~30 muestras, el sincronizador funciona perfectamente. Nos quedan 1 y -1 perfectos que coinciden con los datos de entrada. Ayuda que a este ejemplo no se le haya agregado ningún ruido. Siéntase libre de agregar ruido o cambios de tiempo y ver cómo se comporta el sincronizador. Si usáramos QPSK entonces estaríamos tratando con números complejos, pero el enfoque sería el mismo.

Time Synchronization with Interpolation¶

Los sincronizadores de símbolos tienden a interpolar las muestras de entrada en algún número, por ejemplo, 16, de modo que puedan cambiar en una fracción de muestra. Es poco probable que el retraso aleatorio causado por el canal inalámbrico sea un múltiplo exacto de una muestra, por lo que es posible que el pico del símbolo no se produzca en una muestra. Esto es especialmente cierto en un caso en el que solo se reciben 2 o 4 muestras por símbolo. Al interpolar las muestras, nos brinda la capacidad de muestrear “entre” muestras reales, para alcanzar el pico de cada símbolo. La salida del sincronizador sigue siendo solo 1 muestra por símbolo. Las propias muestras de entrada se interpolan.

Nuestro código Python de sincronización de tiempo que implementamos anteriormente no incluía ninguna interpolación. Para expandir nuestro código, habilite el retraso de tiempo fraccionario que implementamos al principio de este capítulo para que nuestra señal recibida tenga un retraso más realista. Deje la compensación de frecuencia desactivada por ahora. Si vuelve a ejecutar la simulación, encontrará que el sincronizador no logra sincronizarse completamente con la señal. Esto se debe a que no estamos interpolando, por lo que el código no tiene forma de “muestrear entre muestras” para compensar el retraso fraccionario. Agreguemos la interpolación.

Una forma rápida de interpolar una señal en Python es usar scipy. signal.resample o signal.resample_poly. Ambas funciones hacen lo mismo pero funcionan de manera diferente por dentro. Usaremos la última función porque tiende a ser más rápida. Interpolaremos por 16 (esto se elige arbitrariamente, puede probar con diferentes valores), es decir, insertaremos 15 muestras adicionales entre cada muestra. Se puede hacer en una línea de código y debería suceder antes de realizar la sincronización de tiempo (antes del fragmento de código grande previo). Gráficamos el antes y el después para ver la diferencia:

samples_interpolated = signal.resample_poly(samples, 16, 1)

# Plot the old vs new
plt.figure('before interp')
plt.plot(samples,'.-')
plt.figure('after interp')
plt.plot(samples_interpolated,'.-')
plt.show()

Si nos acercamos mucho, vemos que es la misma señal, solo que con 16 veces más puntos:

Example of interpolation a signal, using Python

Con suerte, la razón por la que necesitamos interpolar dentro del bloque de sincronización de tiempo se está aclarando. Estas muestras adicionales nos permitirán tener en cuenta una fracción del retraso de una muestra. Además de calcular samples_interpolated, también tenemos que modificar una línea de código en nuestro sincronizador de tiempo. Cambiaremos la primera línea dentro del bucle while para que se convierta en:

out[i_out] = samples_interpolated[i_in*16 + int(mu*16)]

Hicimos un par de cosas aquí. Primero, ya no podemos usar simplemente i_in como índice de muestra de entrada. Tenemos que multiplicarlo por 16 porque interpolamos nuestras muestras de entrada por 16. Recuerde que el bucle de retroalimentación ajusta la variable mu. Representa el retraso que nos lleva a muestrear en el momento adecuado. Recuerde también que después de calcular el nuevo valor de mu, agregamos la parte entera a i_in. Ahora usaremos la parte restante, que es un flotador de 0 a 1, y representa la fracción de una muestra que necesitamos retrasar. Antes no podíamos retrasar una fracción de muestra, pero ahora sí lo podemos hacer, al menos en incrementos de 16avos de muestra. Lo que hacemos es multiplicar mu por 16 para calcular cuántas muestras de nuestra señal interpolada necesitamos retrasar. Y luego tenemos que redondear ese número, ya que el valor entre paréntesis en última instancia es un índice y debe ser un número entero. Si este párrafo no tiene sentido, intente volver al código inicial de recuperación del reloj de Mueller y Muller y lea también los comentarios junto a cada línea de código.

El resultado de la gráfica actual de este nuevo código debería verse más o menos igual que antes. Todo lo que realmente hicimos fue hacer nuestra simulación más realista agregando el retraso de la muestra fraccionaria, y luego agregamos el interpolador al sincronizador para compensar ese retraso de muestra fraccionaria.

Siéntete libre de jugar con diferentes factores de interpolación, es decir, cambiar todos los 16 a algún otro valor. También puede intentar habilitar el desplazamiento de frecuencia o agregar ruido blanco gaussiano a la señal antes de que se reciba, para ver cómo eso afecta el rendimiento de la sincronización (pista: es posible que deba ajustar ese multiplicador de 0,3).

Si habilitamos solo el desplazamiento de frecuencia usando una frecuencia de 1 kHz, obtenemos el siguiente rendimiento de sincronización de tiempo. Tenemos que mostrar tanto I como Q ahora que agregamos un desplazamiento de frecuencia:

A python simulated signal with a slight frequency offset

Puede que sea difícil de ver, pero la sincronización en tiempo sigue funcionando bien. Se necesitan entre 20 y 30 símbolos antes de que quede enganchado. Sin embargo, hay un patrón sinusoide porque todavía tenemos un desplazamiento de frecuencia, y aprenderemos cómo manejarlo en la siguiente sección.

A continuación se muestra el gráfico IQ (también conocido como gráfico de constelación) de la señal antes y después de la sincronización. Recuerde que puede trazar muestras en un diagrama IQ usando un diagrama de dispersión: plt.plot(np.real(samples), np.imag(samples), '.'). En la siguiente animación hemos omitido específicamente los primeros 30 símbolos. Ocurrieron antes de que finalizara la sincronización en tiempo. Los símbolos de la izquierda están todos aproximadamente en el círculo unitario debido al desplazamiento de frecuencia.

An IQ plot of a signal before and after time synchronization

Para obtener aún más información, podemos observar la constelación a lo largo del tiempo para discernir qué está sucediendo realmente con los símbolos. Al principio, durante un breve período de tiempo, los símbolos no son 0 ni están en el círculo unitario. Ese es el período en el que la sincronización de tiempo encuentra el retraso correcto. Es muy rápido, ¡observa atentamente! El giro es solo el desplazamiento de frecuencia. La frecuencia es un cambio constante de fase, por lo que un desplazamiento de frecuencia provoca el giro del BPSK (creando un círculo en el gráfico estático/persistente anterior).

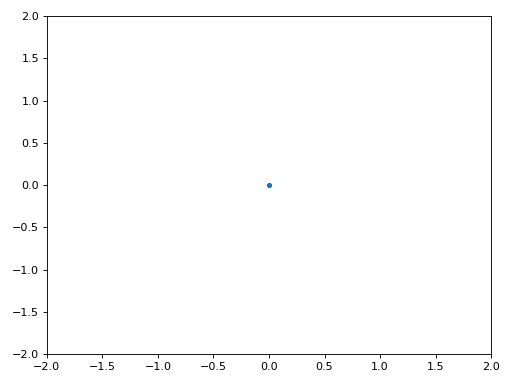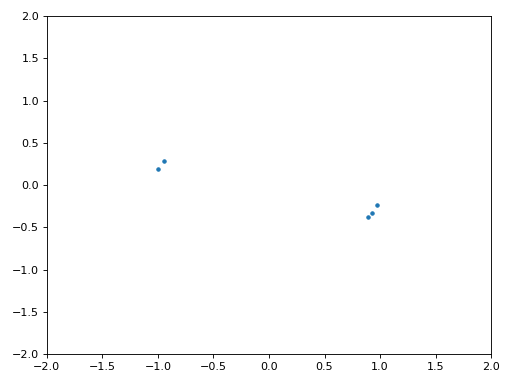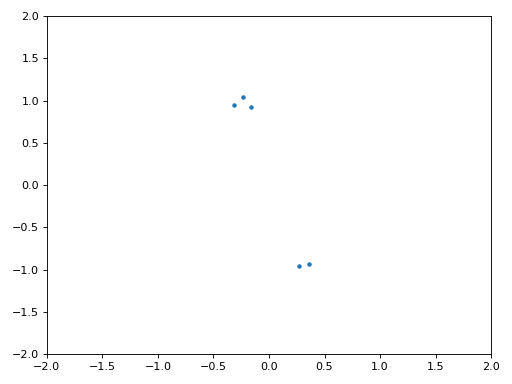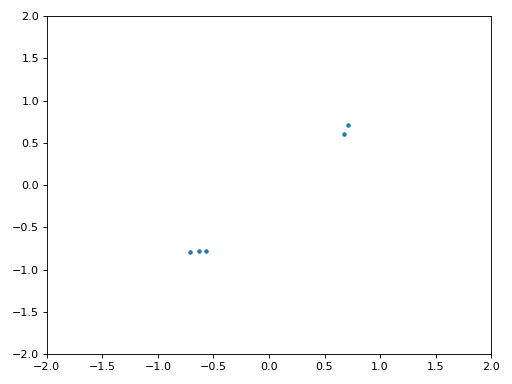
Animation of an IQ plot of BPSK with a frequency offset, showing spinning clusters

Con suerte, al ver un ejemplo de sincronización de tiempo que este sucediendo, tendrá una idea de lo que hace y una idea general de cómo funciona. En la práctica, el bucle while que creamos solo funcionaría en una pequeña cantidad de muestras a la vez (por ejemplo, 1000). Debe recordar el valor de mu entre llamadas a la función de sincronización, así como los últimos valores de out y out_rail.

A continuación examinaremos la sincronización de frecuencia, que dividimos en sincronización de frecuencia gruesa y fina. Lo grueso suele aparecer antes de la sincronización de tiempo, mientras que lo fino viene después.

Sincronización de frecuencia no granular¶

Aunque le decimos al transmisor y al receptor que operen en la misma frecuencia central, habrá un ligero desplazamiento de frecuencia entre los dos debido a imperfecciones en el hardware (por ejemplo, el oscilador) o a un desplazamiento Doppler debido al movimiento. Este desplazamiento de frecuencia será pequeño en relación con la frecuencia portadora, pero incluso un desplazamiento pequeño puede alterar una señal digital. Es probable que la compensación cambie con el tiempo, lo que requerirá un circuito de retroalimentación siempre activo para corregir la compensación. Como ejemplo, el oscilador dentro del Pluto tiene una especificación de compensación máxima de 25 PPM. Eso es 25 partes por millón en relación con la frecuencia central. Si está sintonizado a 2,4 GHz, el desplazamiento máximo sería de +/- 60 kHz. Las muestras que nos proporciona nuestro SDR están en banda base, lo que hace que cualquier compensación de frecuencia se manifieste en esa señal de banda base. Una señal BPSK con un pequeño desplazamiento de portadora se parecerá al gráfico de tiempo siguiente, lo que obviamente no es bueno para demodular bits. Debemos eliminar cualquier compensación de frecuencia antes de la demodulación.

La sincronización de frecuencia generalmente se divide en sincronización gruesa y sincronización fina, donde la sincronización gruesa corrige grandes desplazamientos del orden de kHz o más, mientras que la sincronización fina corrige lo que queda. Lo grueso ocurre antes de la sincronización de tiempo, mientras que lo fino ocurre después.

Matemáticamente, si tenemos una señal de banda base $s(t)$ y está experimentando un desplazamiento de frecuencia (también conocido como portadora) de $f_o$ Hz, podemos representar lo que se recibe como:

$r(t) = s(t) e^{j2\pi f_o t} + n(t)$

donde $n(t)$ es el ruido.

El primer truco que aprenderemos, para realizar una estimación aproximada del desplazamiento de frecuencia (si podemos estimar el desplazamiento de frecuencia, entonces podemos deshacerlo), es tomar el cuadrado de nuestra señal. Ignoremos el ruido por ahora, para simplificar las matemáticas:

$r^2(t) = s^2(t) e^{j4\pi f_o t}$

Veamos qué sucede cuando tomamos el cuadrado de nuestra señal $s(t)$ considerando lo que haría QPSK. Elevar al cuadrado números complejos conduce a un comportamiento interesante, especialmente cuando hablamos de constelaciones como BPSK y QPSK. La siguiente animación muestra lo que sucede cuando elevas QPSK al cuadrado y luego lo vuelves a elevar al cuadrado. Utilicé específicamente QPSK en lugar de BPSK porque puedes ver que cuando elevas QPSK al cuadrado una vez, básicamente obtienes BPSK. Y luego, después de un cuadrado más, se convierte en un grupo. (Gracias a http://ventrella.com/ComplexSquaring/ que creó esta interesante aplicación web).

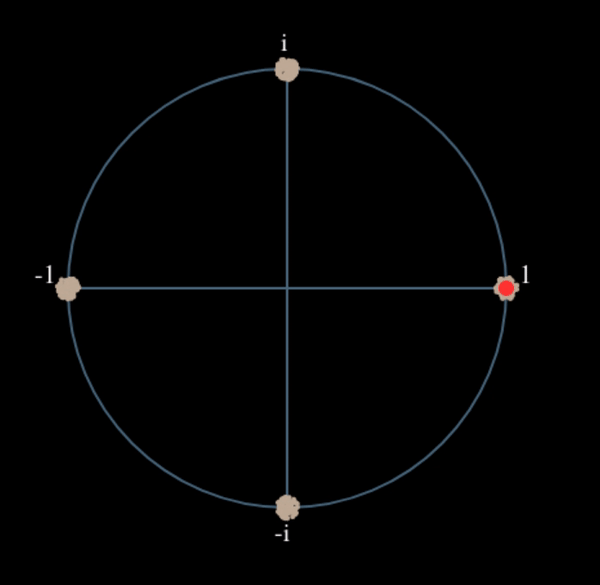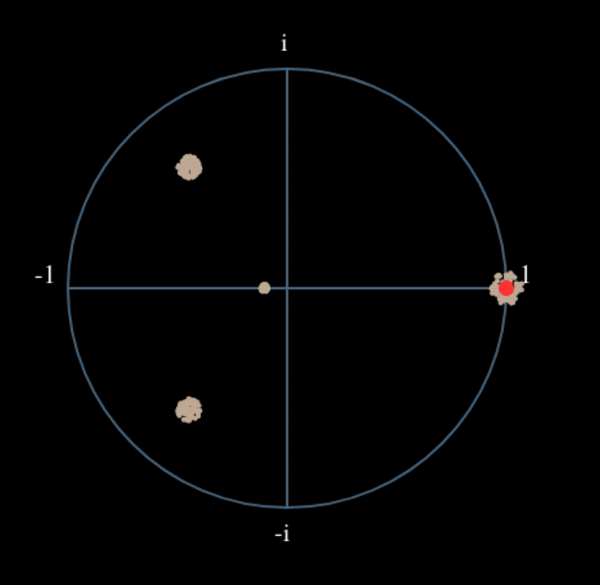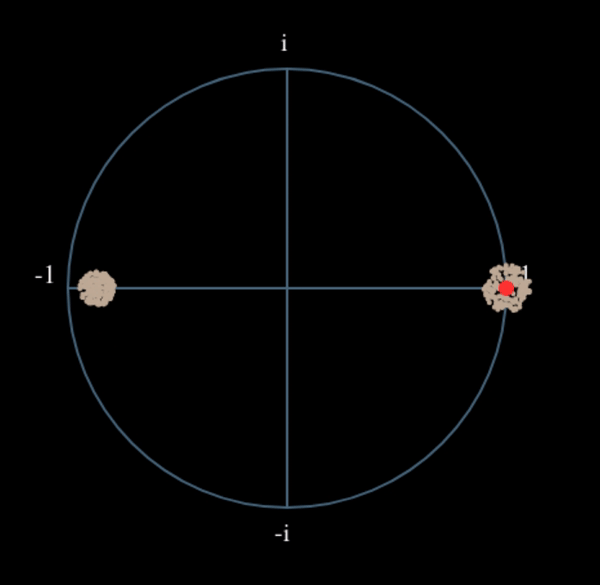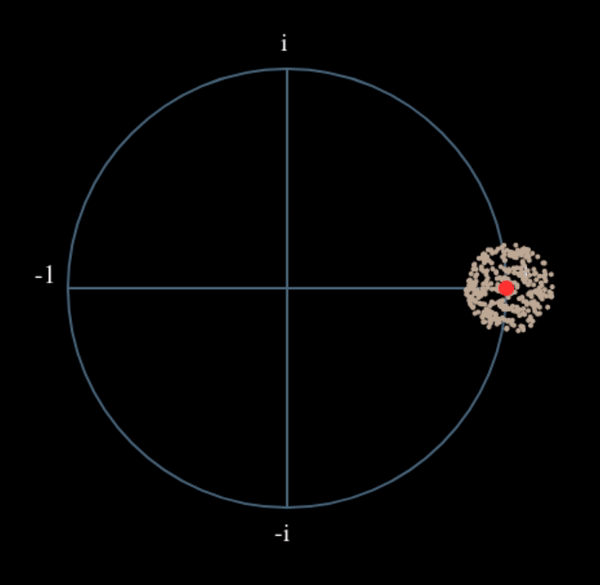
Veamos qué sucede cuando a nuestra señal QPSK se le aplica una pequeña rotación de fase y escala de magnitud, lo cual es más realista:

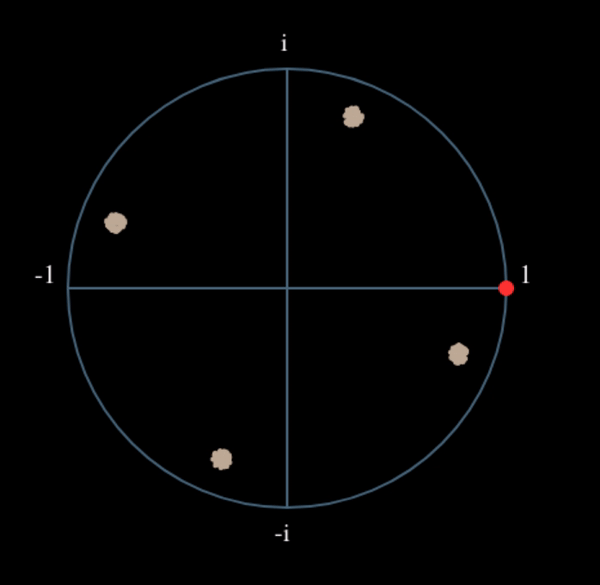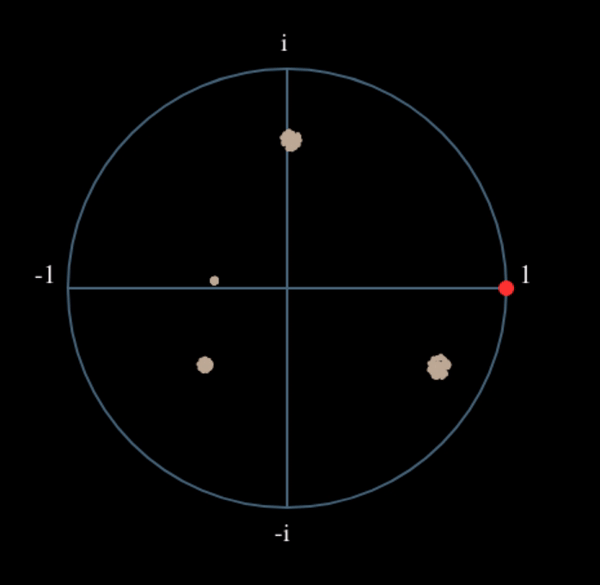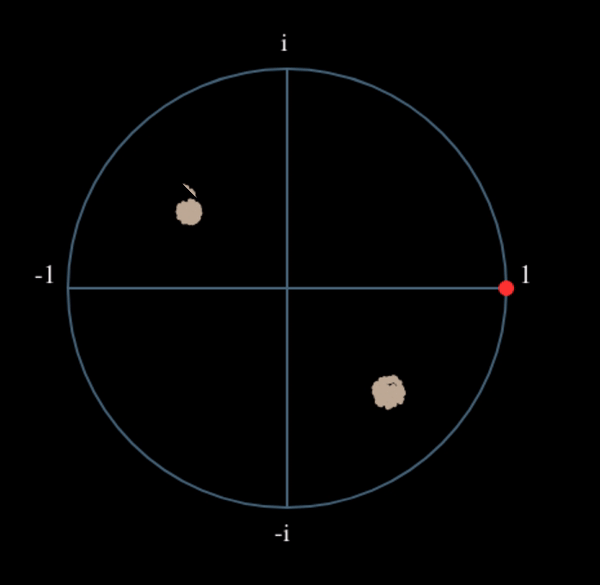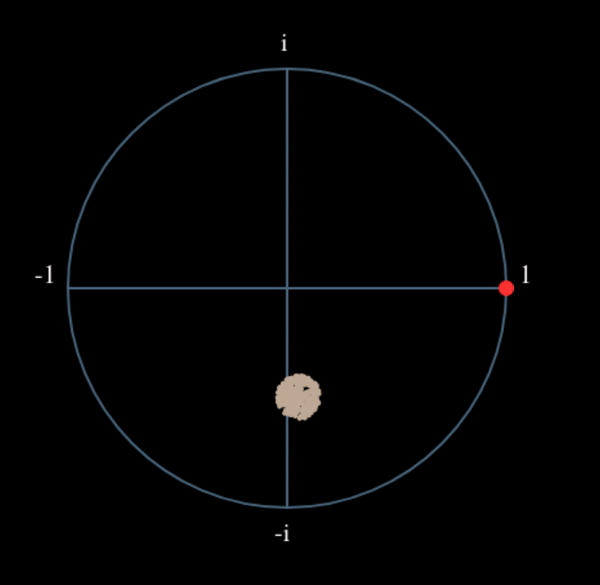
Todavía se convierte en un grupo, sólo que con un cambio de fase. La conclusión principal aquí es que si elevas QPSK al cuadrado dos veces (y BPSK una vez), fusionarás los cuatro grupos de puntos en un solo grupo. ¿Por qué es eso útil? Bueno, al fusionar los grupos, ¡básicamente estamos eliminando la modulación! Si todos los puntos están ahora en el mismo grupo, es como tener un montón de constantes en fila. Es como si ya no hubiera modulación, y lo único que queda es la sinusoide causada por el desplazamiento de frecuencia (también tenemos ruido pero sigamos ignorándolo por ahora). Resulta que tienes que elevar al cuadrado la señal N veces, donde N es el orden del esquema de modulación utilizado, lo que significa que este truco sólo funciona si conoces el esquema de modulación de antemano. La ecuación es realmente:

$r^N(t) = s^N(t) e^{j2N\pi f_o t}$

Para el caso de BPSK tenemos un esquema de modulación de orden 2, por lo que usaremos la siguiente ecuación para la sincronización en frecuencia gruesa:

$r^2(t) = s^2(t) e^{j4\pi f_o t}$

Descubrimos qué sucede con la parte $s(t)$ de la ecuación, pero ¿qué pasa con la parte sinusoide (también conocida como exponencial compleja)? Como podemos ver, está agregando el término $N$ , lo que lo hace equivalente a una sinusoide con una frecuencia de $Nf_o$ en lugar de solo $f_o$ . Un método simple para calcular $f_o$ es tomar la FFT de la señal después de elevarla al cuadrado N veces y ver dónde ocurre el pico. Simulémoslo en Python. Volveremos a generar nuestra señal BPSK y, en lugar de aplicarle un retraso fraccionario, aplicaremos un desplazamiento de frecuencia multiplicando la señal por $e^{j2\pi f_o t}$ tal como lo hicimos en capítulo Filtros para convertir un filtro paso bajo en un filtro paso alto.

Utilizando el código del principio de este capítulo, aplique un desplazamiento de frecuencia de +13 kHz a su señal digital. Podría suceder justo antes o después de que se agregue el retraso fraccionario; no importa cuál. De todos modos, debe suceder después del formador de pulso, pero antes de realizar cualquier función del lado de recepción, como la sincronización de tiempo.

Ahora que tenemos una señal con un desplazamiento de frecuencia de 13 kHz, grafiquemos la FFT antes y después de elevar al cuadrado, para ver qué sucede. A estas alturas ya deberías saber cómo realizar una FFT, incluidas las operaciones abs() y fftshift(). Para este ejercicio no importa si tomas el log o si lo elevas al cuadrado después de tomar los abs().

Primero mire la señal antes de elevarla al cuadrado (solo una FFT normal):

psd = np.fft.fftshift(np.abs(np.fft.fft(samples)))
f = np.linspace(-fs/2.0, fs/2.0, len(psd))
plt.plot(f, psd)
plt.show()

En realidad, no vemos ningún pico asociado con el desplazamiento de la portadora. Está cubierto por nuestra señal.

Ahora con el cuadrado agregado (solo una potencia de 2 porque es BPSK):

# Add this before the FFT line
samples = samples**2

Tenemos que acercarnos mucho para ver en qué frecuencia está el pico:

Puede intentar aumentar la cantidad de símbolos simulados (por ejemplo, 1000 símbolos) para que tengamos suficientes muestras con las que trabajar. Cuantas más muestras entren en nuestra FFT, más precisa será nuestra estimación del desplazamiento de frecuencia. Sólo como recordatorio, el código anterior debe aparecer antes del sincronizador de tiempo.

El pico de frecuencia desplazada aparece en $Nf_o$ . Necesitamos dividir este contenedor (26,6 kHz) por 2 para encontrar nuestra respuesta final, que está muy cerca del desplazamiento de frecuencia de 13 kHz que aplicamos al comienzo del capítulo. Si hubieras jugado con ese número y ya no es 13 kHz, está bien. Solo asegúrese de saber en qué lo configuró.

Debido a que nuestra frecuencia de muestreo es de 1 MHz, las frecuencias máximas que podemos ver son de -500 kHz a 500 kHz. Si llevamos nuestra señal a la potencia de N, eso significa que solo podemos “ver” desplazamientos de frecuencia hasta $500e3/N$ , o en el caso de BPSK +/- 250 kHz. Si estuviéramos recibiendo una señal QPSK, entonces solo sería +/- 125 kHz, y el desplazamiento de la portadora mayor o menor que eso estaría fuera de nuestro rango usando esta técnica. Para darle una idea del cambio Doppler, si estuviera transmitiendo en la banda de 2,4 GHz y el transmisor o el receptor viajaba a 60 mph (lo que importa es la velocidad relativa), causaría un cambio de frecuencia de 214 Hz. La compensación debida a un oscilador de baja calidad probablemente será el principal culpable de esta situación.

En realidad, la corrección de este desplazamiento de frecuencia se realiza exactamente como simulamos el desplazamiento en primer lugar: multiplicando por una exponencial compleja, excepto que con un signo negativo ya que queremos eliminar el desplazamiento.

max_freq = f[np.argmax(psd)]
Ts = 1/fs # calc sample period
t = np.arange(0, Ts*len(samples), Ts) # create time vector
samples = samples * np.exp(-1j*2*np.pi*max_freq*t/2.0)

Depende de ti si desea corregirlo o cambiar el desplazamiento de frecuencia inicial que aplicamos al principio a un número más pequeño (como 500 Hz) para probar la sincronización fina de frecuencia que ahora aprenderemos a hacer.

Sincronización de frecuencia fina¶

A continuación cambiaremos de marcha a sincronización fina en frecuencia. El truco anterior es más para sincronización aproximada y no es una operación de bucle cerrado (tipo retroalimentación). Pero para una sincronización precisa de frecuencias necesitaremos un bucle de retroalimentación a través del cual transmitamos muestras, que una vez más será una forma de PLL. Nuestro objetivo es conseguir que la compensación de frecuencia sea cero y mantenerla allí, incluso si la compensación cambia con el tiempo. Tenemos que realizar un seguimiento continuo de la compensación. Las técnicas de sincronización fina en frecuencia funcionan mejor con una señal que ya se ha sincronizado en el tiempo a nivel de símbolo, por lo que el código que analizamos en esta sección vendrá después de la sincronización de tiempo.

Usaremos una técnica llamada Costas Loop. Es una forma de PLL diseñada específicamente para la corrección de compensación de frecuencia portadora para señales digitales como BPSK y QPSK. Fue inventado por John P. Costas en General Electric en la década de 1950 y tuvo un gran impacto en las comunicaciones digitales modernas. Costas Loop eliminará el desplazamiento de frecuencia y al mismo tiempo arreglará cualquier desplazamiento de fase. La energía está alineada con el eje I. La frecuencia es solo un cambio de fase para que puedan rastrearse como uno solo. El Costas Loop se resume utilizando el siguiente diagrama (tenga en cuenta que los 1/2 se han omitido de las ecuaciones porque funcionalmente no importan).

Costas loop diagram including math expressions, it is a form of PLL used in RF signal processing

El oscilador controlado por voltaje (VCO) es simplemente un generador de ondas sen/cos que utiliza una frecuencia basada en la entrada. En nuestro caso, al estar simulando un canal inalámbrico, no se trata de un voltaje, sino de un nivel representado por una variable. Determina la frecuencia y fase de las ondas sinusoidales y coseno generadas. Lo que hace es multiplicar la señal recibida por una sinusoide generada internamente, en un intento de deshacer el desplazamiento de frecuencia y fase. Este comportamiento es similar a cómo un SDR realiza una conversión descendente y crea las ramas I y Q.

A continuación se muestra el código Python que es nuestro Costas Loop:

N = len(samples)
phase = 0
freq = 0
# These next two params is what to adjust, to make the feedback loop faster or slower (which impacts stability)
alpha = 0.132
beta = 0.00932
out = np.zeros(N, dtype=np.complex)
freq_log = []
for i in range(N):
    out[i] = samples[i] * np.exp(-1j*phase) # adjust the input sample by the inverse of the estimated phase offset
    error = np.real(out[i]) * np.imag(out[i]) # This is the error formula for 2nd order Costas Loop (e.g. for BPSK)

    # Advance the loop (recalc phase and freq offset)
    freq += (beta * error)
    freq_log.append(freq * fs / (2*np.pi)) # convert from angular velocity to Hz for logging
    phase += freq + (alpha * error)

    # Optional: Adjust phase so its always between 0 and 2pi, recall that phase wraps around every 2pi
    while phase >= 2*np.pi:
        phase -= 2*np.pi
    while phase < 0:
        phase += 2*np.pi

# Plot freq over time to see how long it takes to hit the right offset
plt.plot(freq_log,'.-')
plt.show()

Hay mucho aquí, así que repasémoslo. Algunas líneas son simples y otras súper complicadas. samples es nuestra entrada y out son las muestras de salida. phase y frequency son como mu del código de sincronización en tiempo. Contienen las estimaciones para los desplazamientos actuales, y en cada iteración del bucle creamos las muestras de salida multiplicando las muestras de entrada por np.exp(-1j*phase). La variable error contiene la métrica de “error”, y para que Costas Loop de segundo orden es una ecuación muy simple. Multiplicamos la parte real de la muestra (I) por la parte imaginaria (Q), y como Q debe ser igual a cero para BPSK, la función de error se minimiza cuando no hay ningún desplazamiento de fase o frecuencia que provoque que la energía se desplace de I. a Q. Para un Costas Loop de cuarto orden, sigue siendo relativamente simple, pero no es una sola línea, ya que tanto I como Q tendrán energía incluso cuando no haya compensación de fase o frecuencia, para QPSK. Si tiene curiosidad sobre cómo se ve, haga clic a continuación, pero no lo usaremos en nuestro código por ahora. La razón por la que esto funciona para QPSK es porque cuando tomas el valor absoluto de I y Q, obtendrás +1+1j, y si no hay compensación de fase o frecuencia, entonces la diferencia entre el valor absoluto de I y Q debería ser cercana. a cero.

Ecuación de error Costas Loop de 4to orden (para aquellos curiosos)

# For QPSK
def phase_detector_4(sample):
    if sample.real > 0:
        a = 1.0
    else:
        a = -1.0
    if sample.imag > 0:
        b = 1.0
    else:
        b = -1.0
    return a * sample.imag - b * sample.real

Las variables alpha y beta definen qué tan rápido se actualiza la fase y la frecuencia, respectivamente. Hay alguna teoría detrás de por qué elegí esos dos valores; sin embargo, no lo abordaremos aquí. Si tienes curiosidad, puedes intentar modificar alpha y/o beta para ver qué sucede.

Registramos el valor de freq en cada iteración para poder graficarlo al final, para ver cómo el Costas Loop converge hacia el desplazamiento de frecuencia correcto. Tenemos que multiplicar freq por la frecuencia de muestreo y convertir de frecuencia angular a Hz, dividiendo por $2\pi$ . Tenga en cuenta que si realizó la sincronización de tiempo antes del Costas Loop, también tendrá que dividir por su sps (por ejemplo, 8), porque las muestras que salen de la sincronización de tiempo tienen una velocidad igual a su original. frecuencia de muestreo dividida por sps.

Por último, después de recalcular la fase, agregamos o eliminamos suficientes $2 \pi$ para mantener la fase entre 0 y $2 \pi$ , lo que ajusta la fase.

Nuestra señal antes y después del Costas Loop se ve así:

Python simulation of a signal before and after using a Costas Loop

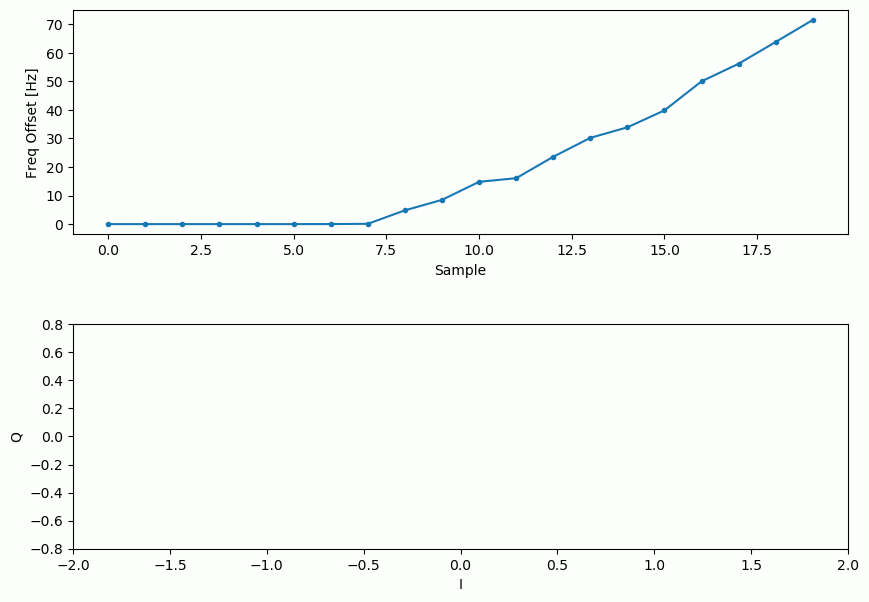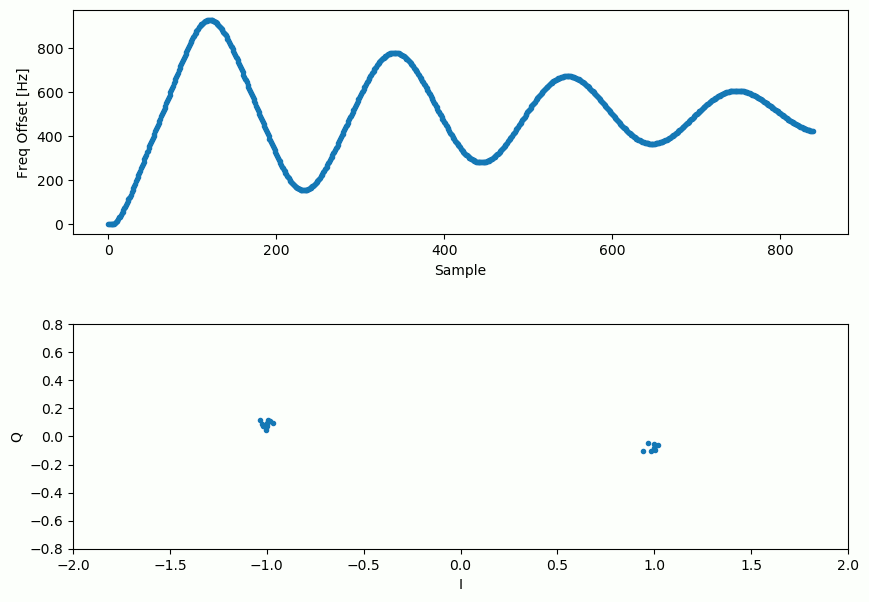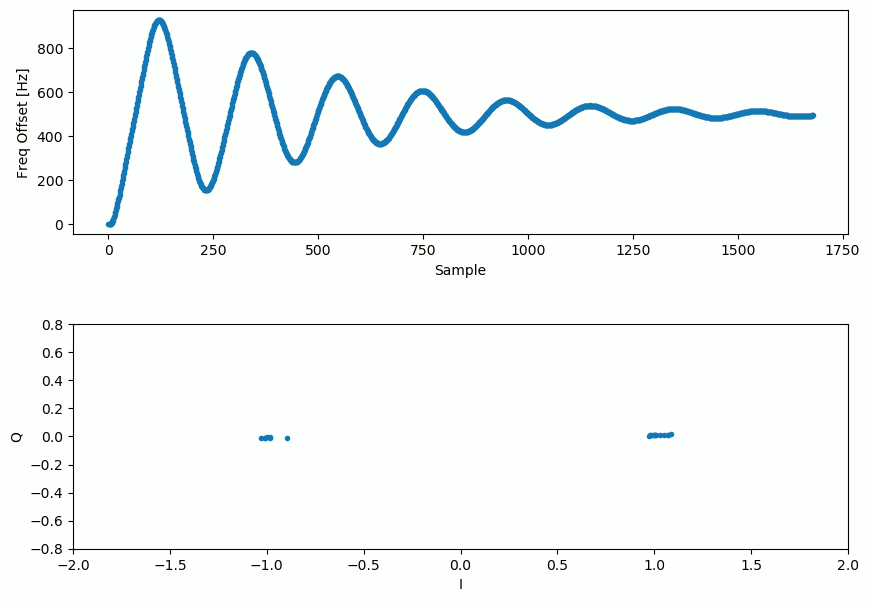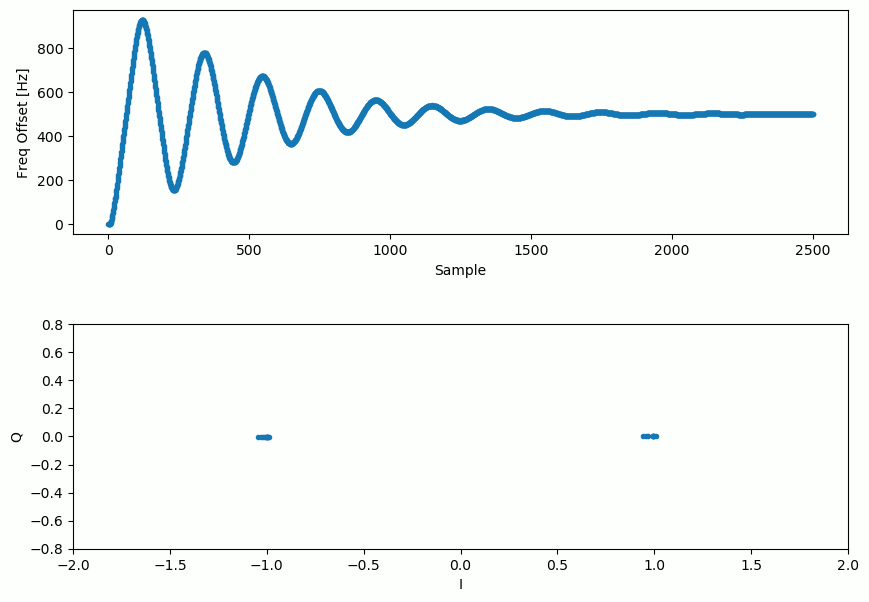
Y la estimación del desplazamiento de frecuencia a lo largo del tiempo, estableciendo el desplazamiento correcto (en esta señal de ejemplo se utilizó un desplazamiento de -300 Hz):

../_images/costas-loop-freq-tracking.svg

Se necesitan casi 70 muestras para que el algoritmo se enganche en el desplazamiento de frecuencia correcto. Puede ver que en mi ejemplo simulado quedaron alrededor de -300 Hz después de la sincronización de frecuencia aproximada. El tuyo puede variar. Como mencioné antes, puedes desactivar la sincronización de frecuencia aproximada y establecer el desplazamiento de frecuencia inicial en el valor que desees y ver si Costas Loop lo resuelve.

Costas Loop, además de eliminar el desplazamiento de frecuencia, alineó nuestra señal BPSK para que esté en la porción I, haciendo que Q vuelva a ser cero. Es un efecto secundario conveniente del Costas Loop y permite que el Costas Loop actúe esencialmente como nuestro demodulador. Ahora todo lo que tenemos que hacer es tomar I y ver si es mayor o menor que cero. En realidad, no sabremos cómo hacer que 0 y 1 sean negativos y positivos porque puede haber o no una inversión; no hay forma de que Costas Loop (o nuestra sincronización en tiempo) lo sepa. Ahí es donde entra en juego la codificación diferencial. Elimina la ambigüedad porque los 1 y 0 se basan en si el símbolo cambió o no, no en si era +1 o -1. Si agregamos codificación diferencial, todavía estaríamos usando BPSK. Estaríamos agregando un bloque de codificación diferencial justo antes de la modulación en el lado de transmisión y justo después de la demodulación en el lado de recepción.

A continuación se muestra una animación de la sincronización de tiempo más la sincronización de frecuencia en ejecución. La sincronización de tiempo en realidad ocurre casi de inmediato, pero la sincronización de frecuencia requiere casi toda la animación para establecerse por completo, y esto se debe a que alpha y beta se establecieron demasiado bajos, en 0,005 y 0,001 respectivamente. El código utilizado para generar esta animación se puede encontrar aqui.

Sincronización de Trama¶

Hemos discutido cómo corregir cualquier desplazamiento en tiempo, frecuencia y fase en nuestra señal recibida. Pero la mayoría de los protocolos de comunicaciones modernos no se limitan a transmitir bits al 100% del ciclo de trabajo. En su lugar, utilizan paquetes/tramas. En el receptor debemos poder identificar cuándo comienza una nueva trama. Habitualmente, el encabezado de la trama (en la capa MAC) contiene cuántos bytes hay en la trama. Podemos usar esa información para saber cuánto mide la trama, por ejemplo, en unidades, muestras o símbolos. No obstante, detectar el inicio del fotograma es una tarea completamente independiente. A continuación se muestra un ejemplo de estructura de trama WiFi. Observe cómo lo primero que se transmite es un encabezado de capa PHY, y la primera mitad de ese encabezado es un “preámbulo”. Este preámbulo contiene una secuencia de sincronización que el receptor utiliza para detectar el inicio de las tramas, y es una secuencia conocida por el receptor de antemano.

Un método común y sencillo para detectar estas secuencias en el receptor es correlacionar las muestras recibidas con la secuencia conocida. Cuando ocurre la secuencia, esta correlación cruzada se asemeja a una autocorrelación (con ruido agregado). Normalmente, las secuencias elegidas para los preámbulos tendrán buenas propiedades de autocorrelación, como que la autocorrelación de la secuencia crea un único pico fuerte en 0 y ningún en otro pico. Un ejemplo son los códigos Barker, en 802.11/WiFi se utiliza una secuencia Barker de longitud 11 para las velocidades de 1 y 2 Mbit/s:

+1 +1 +1 −1 −1 −1 +1 −1 −1 +1 −1

Puedes considerarlo como 11 símbolos BPSK. Podemos observar la autocorrelación de esta secuencia muy fácilmente en Python:

import numpy as np
import matplotlib.pyplot as plt
x = [1,1,1,-1,-1,-1,1,-1,-1,1,-1]
plt.plot(np.correlate(x,x,'same'),'.-')
plt.grid()
plt.show()

Puedes ver que 11 es longitud de la secuencia con un pico en el centro y -1 o 0 para todos los demás retrasos. Funciona bien para encontrar el inicio de una trama porque esencialmente integra 11 símbolos de energía en un intento de crear un bit pico en la salida de la correlación cruzada. De hecho, la parte más difícil de realizar la detección de inicio de trama es encontrar un buen umbral. No se desea que lo activen tramas que en realidad no son parte de su protocolo. Eso significa que, además de la correlación cruzada, también hay que realizar algún tipo de normalización de potencia, que no consideraremos aquí. Al decidir un umbral, hay que hacer un equilibrio entre la probabilidad de detección y la probabilidad de falsas alarmas. Recuerde que el encabezado de la trama en sí tendrá información, por lo que algunas falsas alarmas están bien; rápidamente descubrirá que en realidad no es una trama cuando vaya a decodificar el encabezado y el CRC inevitablemente falla (porque en realidad no era una trama). Sin embargo, si bien algunas falsas alarmas están bien, pasar por alto la detección de una trama es malo.

Otra secuencia con grandes propiedades de autocorrelación son las secuencias de Zadoff-Chu, que se utilizan en LTE. Tienen la ventaja de estar en conjuntos; puede tener varias secuencias diferentes que tengan buenas propiedades de autocorrelación, pero no se activarán entre sí (es decir, también buenas propiedades de correlación cruzada, cuando correlacione diferentes secuencias en el conjunto). Gracias a esa característica, a diferentes estaciones celulares se les asignarán diferentes secuencias para que un teléfono no solo pueda encontrar el inicio de la trama sino también saber de qué torre está recibiendo.