19. Phased Arrays con Phaser¶

En este capítulo usaremos el Analog Devices Phaser, (también conocido como CN0566 o ADALM-PHASER), que es un Phased Array SDR de bajo costo de 8 canales que combina PlutoSDR, Raspberry Pi y beamformers ADAR1000, diseñado para operar alrededor de 10,25 GHz. Cubriremos los pasos de configuración y calibración y luego veremos algunos ejemplos de formación de haces en Python. Para aquellos que no tienen una Phaser, hemos incluido capturas de pantalla y animaciones de lo que vería el usuario.

Introducción al Phased Arrays¶

Proximamente!

Revisión del Hardware¶

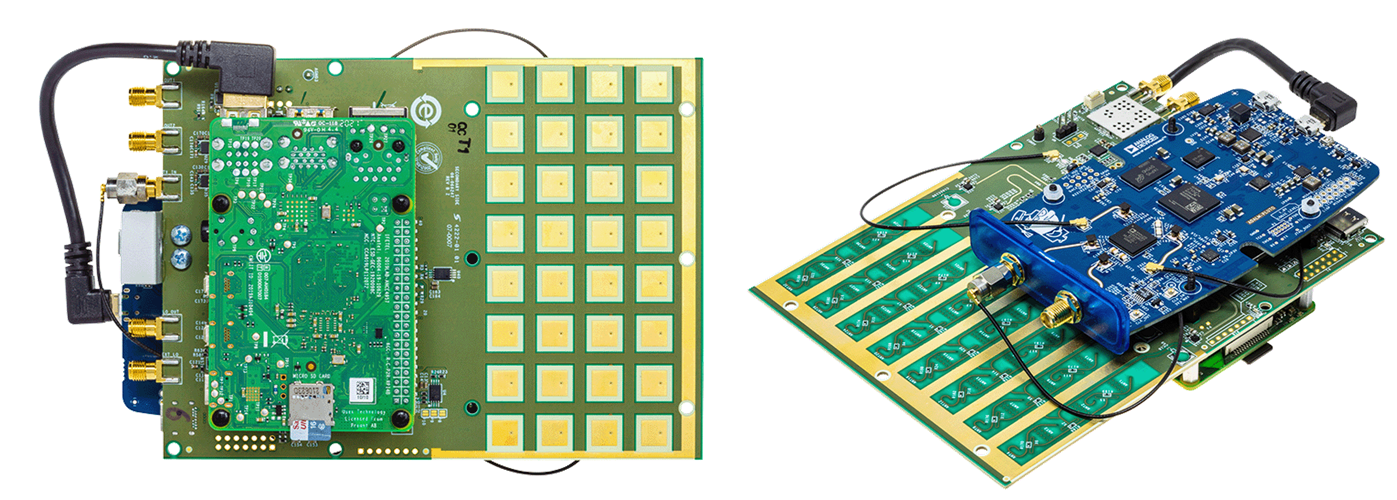
El Phaser es una placa única que contiene un Phased Array y muchos otros componentes, con una Raspberry Pi conectada en un lado y un Pluto montado en el otro lado. El diagrama de bloques de alto nivel se muestra a continuación. Algunos elementos a tener en cuenta:

Aunque parece una matriz 2D de 32 elementos, en realidad es una matriz 1D de 8 elementos.
Se utilizan ambos canales de recepción en el Pluto (el segundo canal usa un conector u.FL)
El LO a bordo se utiliza para convertir la señal recibida de aproximadamente 10,25 GHz a aproximadamente 2 GHz, para que el Pluto pueda recibirla.
Cada ADAR1000 tiene cuatro desfasadores con ganancia ajustable y los cuatro canales se suman antes de enviarse al Pluto.
El Phaser contiene esencialmente dos “subarreglos”, cada uno de los cuales contiene cuatro canales.
No se muestran a continuación las señales GPIO y seriales de Raspberry Pi utilizadas para controlar varios componentes en Phaser.

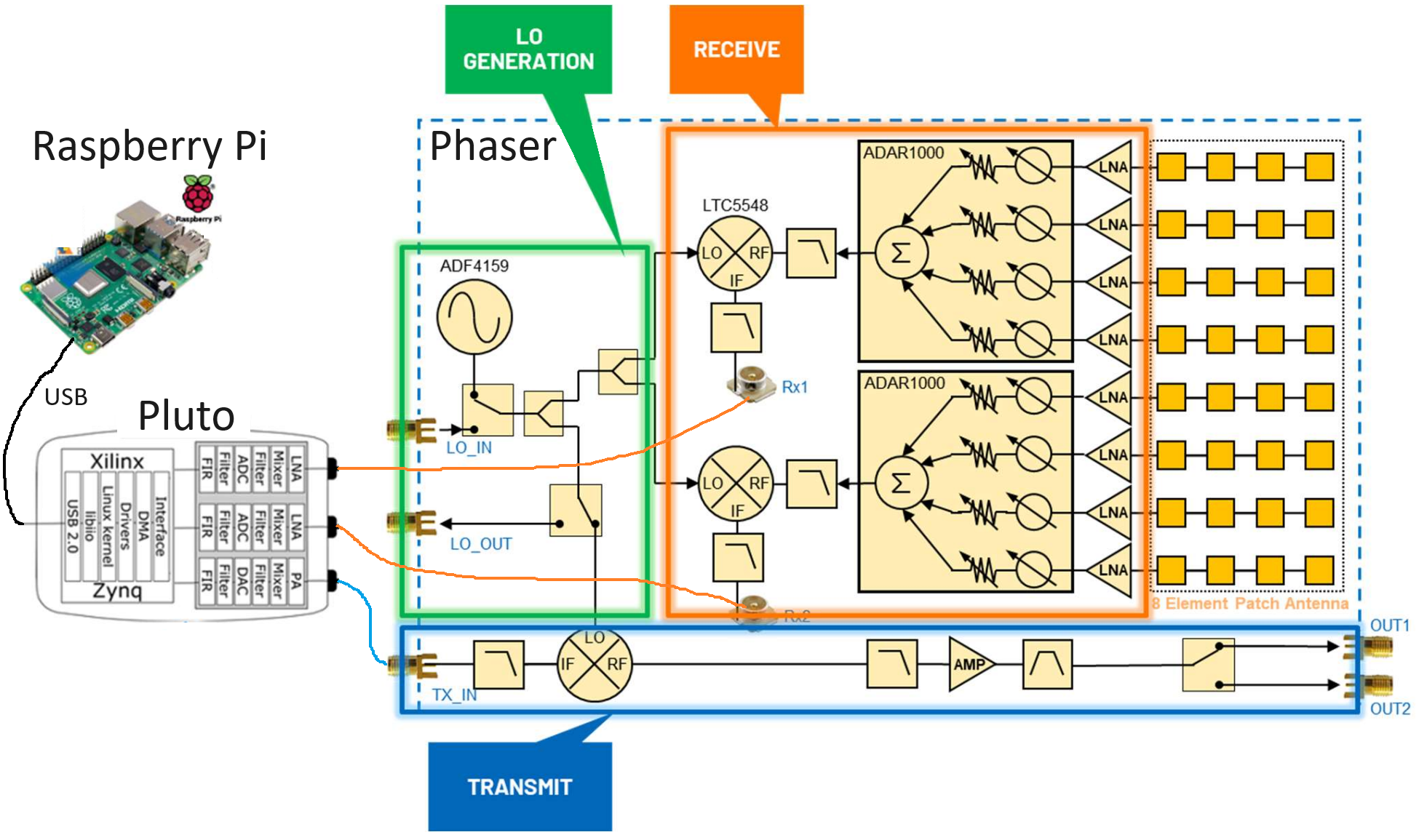
The components of the Phaser (CN0566) including ADF4159, LTC5548, ADAR1000

Por ahora ignoremos el lado de transmisión del Phaser, ya que en este capítulo solo usaremos el dispositivo HB100 como transmisor de prueba. El ADF4159 es un sintetizador de frecuencia que produce un tono de hasta 13 GHz de frecuencia, lo que llamamos oscilador local o LO. Este LO se alimenta a un mezclador, el LTC5548, que es capaz de realizar una conversión ascendente o descendente, aunque lo usaremos para una conversión descendente. Para la conversión descendente, toma el LO y una señal entre 2 y 14 GHz y los multiplica, lo que realiza un cambio de frecuencia. La señal convertida resultante puede oscilar entre DC y 6 GHz, aunque nuestro objetivo será alrededor de 2 GHz. El ADAR1000 es un beamforming analógico de 4 canales, por lo que el Phaser utiliza dos de ellos. Un beamforming analógico tiene desfasadores y ganancia ajustables independientemente para cada canal, lo que permite que cada canal se retrase y se atenúe antes de sumarse en el dominio analógico (lo que da como resultado un solo canal). En el Phaser, cada ADAR1000 emite una señal que se convierte y luego se recibe en el Pluto. Usando Raspberry Pi podemos controlar la fase y la ganancia de los ocho canales en tiempo real para realizar la formación de haces. También tenemos la opción de realizar procesamiento de matriz/beamforming digital de dos canales, que se analiza en el siguiente capítulo.

Para aquellos interesados, a continuación se proporciona un diagrama de bloques un poco más detallado.

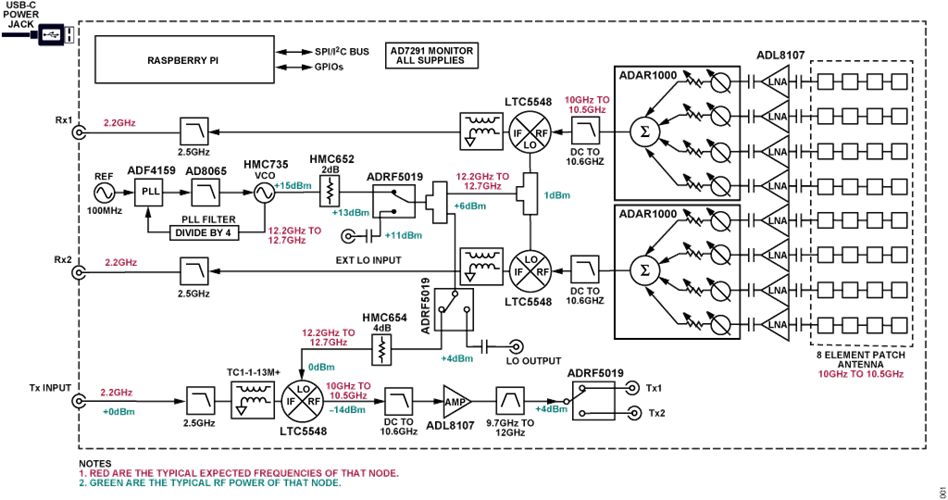
Detailed block diagram of the Phaser (CN0566)

Preparación de la tarjeta SD¶

Asumiremos que está utilizando la Raspberry Pi integrada en el Phaser (directamente, con un monitor/teclado/ratón). Esto simplifica la configuración, ya que Analog Devices publica una imagen de tarjeta SD prediseñada con todos los controladores y software necesarios. Puede descargar la imagen de la tarjeta SD y encontrar instrucciones de imágenes SD aqui. La imagen está basada en el sistema operativo Raspberry Pi e incluye todo el software que necesitará ya instalado.

Preparación del hardware¶

Conecte el puerto micro-USB CENTRAL del Pluto a la Raspberry Pi
Opcionalmente, enrosque con cuidado el trípode en el soporte del trípode.
Asumiremos que estás usando una pantalla HDMI, un teclado USB y un mouse USB conectados a la Raspberry pi.
Encienda la placa Pi y Phaser a través del puerto tipo C del Phaser (CN0566), es decir, NO conecte una fuente al USB C de Raspberry Pi.

Instalación de software¶

Una vez que haya booteado la Raspberry Pi usando la imagen preconstruida, usando el usuario/contraseña analog/analog predeterminado, se recomienda ejecutar los siguientes pasos:

wget https://github.com/mthoren-adi/rpi_setup_stuff/raw/main/phaser/phaser_sdcard_setup.sh
sudo chmod +x phaser_sdcard_setup.sh
./phaser_sdcard_setup.sh
sudo reboot

sudo raspi-config

Para obtener más ayuda con la configuración de Phaser, consulte la Phaser wiki quickstart page.

Configuración del HB100¶

El HB100 que viene con el Phaser es un módulo de radar Doppler de bajo costo que usaremos como transmisor de prueba, ya que transmite un tono continuo alrededor de los 10 GHz. Funciona con 2 baterías AA o una fuente de mesa de 3V, y cuando esté encendido, tendrá un LED rojo fijo.

Debido a que el HB100 es de bajo costo y utiliza componentes de RF baratos, su frecuencia de transmisión varía de una unidad a otra, en cientos de MHz, que es un rango mayor que el ancho de banda más alto que podemos recibir usando el Pluto (56 MHz). Entonces, para asegurarnos de que estamos sintonizando nuestro Pluto y nuestro convertidor descendente de manera que siempre reciban la señal HB100, debemos determinar la frecuencia de transmisión del HB100. Esto se hace usando una aplicación de ejemplo de Analog Devices, que realiza un barrido de frecuencia y calcula FFT mientras busca un pico. Asegúrese de que su HB100 esté encendido y cerca del Phaser y luego ejecute la utilidad con:

cd ~/pyadi-iio/examples/phaser
python phaser_find_hb100.py

Debería crear un archivo llamado hb100_freq_val.pkl en el mismo directorio. Este archivo contiene la frecuencia de transmisión del HB100 en Hz (decapada, por lo que no se puede ver en texto sin formato) que usaremos en el siguiente paso.

Calibración¶

Por último, necesitamos calibrar el phased array. Esto requiere sostener el HB100 apuntando al arreglo (0 grados). Del lado del HB100 con el código de barras es el lado que transmite la señal, por lo que esa cara debe mantenerse a unos metros de distancia del Phaser, justo enfrente y centrada, y luego apuntar directamente al Phaser. En el siguiente paso puedes experimentar con diferentes ángulos y orientaciones, pero por ahora ejecutemos la utilidad de calibración:

python phaser_examples.py cal

Esto creará dos archivos pickle: fase_cal_val.pkl y ganancia_cal_val.pkl, en el mismo directorio. Cada uno contiene una serie de 8 números correspondientes a la fase y los ajustes de ganancia necesarios para calibrar cada canal. Estos valores son únicos para cada Phaser, como pueden variar durante la fabricación. Las ejecuciones posteriores de esta utilidad generarán valores ligeramente diferentes, lo cual es normal.

Aplicación de ejemplo¶

Ahora que hemos calibrado nuestro Phaser y encontramos la frecuencia HB100, podemos ejecutar la aplicación de ejemplo que proporciona Analog Devices.

python phaser_gui.py

Si marca la casilla de verificación “Actualizar datos automáticamente” en la parte inferior izquierda, debería comenzar a ejecutarse. Debería ver algo similar a lo siguiente cuando sostenga el HB100 apuntando al Phaser.

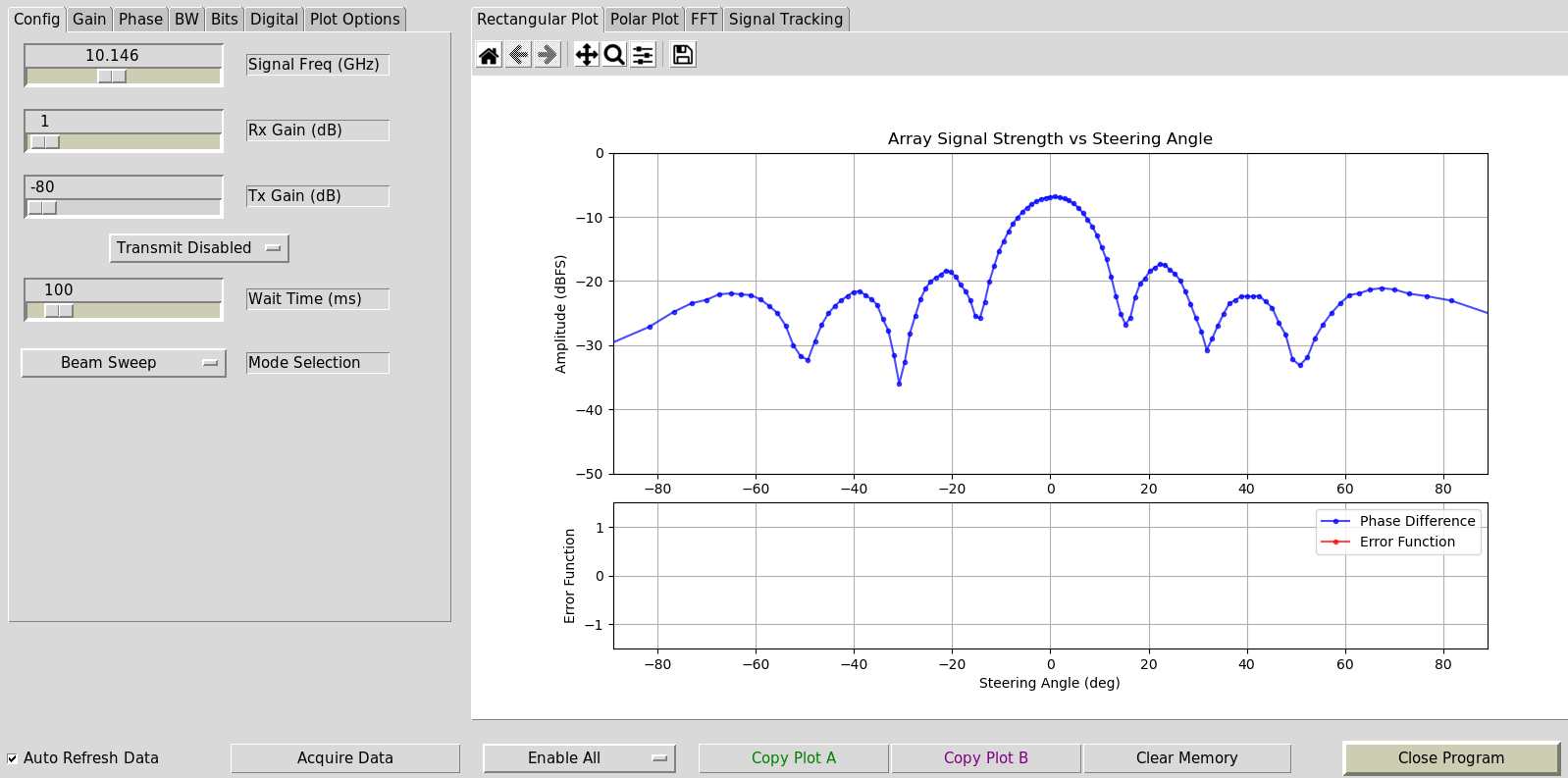
Phaser example GUI tool by Analog Devices

Phaser en Python¶

Ahora nos sumergiremos en la parte práctica en Python. Para aquellos que no tienen una Phaser, se proporcionan capturas de pantalla y animaciones.

Inicialización del Phaser y Pluto¶

El siguiente código Python configura nuestro Phaser y Pluto. En este punto, ya debería haber ejecutado los pasos de calibración, que producen tres archivos pickle. Asegúrese de ejecutar el siguiente script de Python desde el mismo directorio que estos archivos pickle.

Hay muchas configuraciones con las que lidiar, por lo que está bien si no absorbes todo el fragmento de código a continuación, solo ten en cuenta que estamos usando una frecuencia de muestreo de 30 MHz, ganancia manual que configuramos muy baja, configuramos todos los elementos de ganancia al mismo valor y apuntar el phase array de frente (0 grados).

import time
import sys
import matplotlib.pyplot as plt
import numpy as np
import pickle
from adi import ad9361
from adi.cn0566 import CN0566

phase_cal = pickle.load(open("phase_cal_val.pkl", "rb"))
gain_cal = pickle.load(open("gain_cal_val.pkl", "rb"))
signal_freq = pickle.load(open("hb100_freq_val.pkl", "rb"))
d = 0.014  # element to element spacing of the antenna

phaser = CN0566(uri="ip:localhost")
sdr = ad9361(uri="ip:192.168.2.1")
phaser.sdr = sdr
print("PlutoSDR and CN0566 connected!")

time.sleep(0.5) # recommended by Analog Devices

phaser.configure(device_mode="rx")

# Set all antenna elements to half scale - a typical HB100 will have plenty of signal power.
gain = 64 # 64 is about half scale
for i in range(8):
    phaser.set_chan_gain(i, gain, apply_cal=False)

# Aim the beam at boresight (zero degrees)
phaser.set_beam_phase_diff(0.0)

# Misc SDR settings, not super critical to understand
sdr._ctrl.debug_attrs["adi,frequency-division-duplex-mode-enable"].value = "1"
sdr._ctrl.debug_attrs["adi,ensm-enable-txnrx-control-enable"].value = "0" # Disable pin control so spi can move the states
sdr._ctrl.debug_attrs["initialize"].value = "1"
sdr.rx_enabled_channels = [0, 1] # enable Rx1 and Rx2
sdr._rxadc.set_kernel_buffers_count(1) # No stale buffers to flush
sdr.tx_hardwaregain_chan0 = int(-80) # Make sure the Tx channels are attenuated (or off)
sdr.tx_hardwaregain_chan1 = int(-80)

# These settings are basic PlutoSDR settings we have seen before
sample_rate = 30e6
sdr.sample_rate = int(sample_rate)
sdr.rx_buffer_size = int(1024)  # samples per buffer
sdr.rx_rf_bandwidth = int(10e6)  # analog filter bandwidth

# Manually gain (no automatic gain control) so that we can sweep angle and see peaks/nulls
sdr.gain_control_mode_chan0 = "manual"
sdr.gain_control_mode_chan1 = "manual"
sdr.rx_hardwaregain_chan0 = 10 # dB, 0 is the lowest gain.  the HB100 is pretty loud
sdr.rx_hardwaregain_chan1 = 10 # dB

sdr.rx_lo = int(2.2e9) # The Pluto will tune to this freq

# Set the Phaser's PLL (the ADF4159 onboard) to downconvert the HB100 to 2.2 GHz plus a small offset
offset = 1000000 # add a small arbitrary offset just so we're not right at 0 Hz where there's a DC spike
phaser.lo = int(signal_freq + sdr.rx_lo - offset)

Reciviendo muestras del Pluto¶

En este punto, el Phaser y el Pluto están configurados y listos para funcionar. Ahora podemos empezar a recibir datos del Pluto. Tomemos un solo lote de 1024 muestras y luego tomemos la FFT de cada uno de los dos canales.

# Grab some samples (whatever we set rx_buffer_size to), remember we are receiving on 2 channels at the same time
data = sdr.rx()

# Take FFT
PSD0 = 10*np.log10(np.abs(np.fft.fftshift(np.fft.fft(data[0])))**2)
PSD1 = 10*np.log10(np.abs(np.fft.fftshift(np.fft.fft(data[1])))**2)
f = np.linspace(-sample_rate/2, sample_rate/2, len(data[0]))

# Time plot helps us check that we see the HB100 and that we're not saturated (ie gain isnt too high)
plt.subplot(2, 1, 1)
plt.plot(data[0].real) # Only plot real part
plt.plot(data[1].real)
plt.xlabel("Data Point")
plt.ylabel("ADC output")

# PSDs show where the HB100 is and verify both channels are working
plt.subplot(2, 1, 2)
plt.plot(f/1e6, PSD0)
plt.plot(f/1e6, PSD1)
plt.xlabel("Frequency [MHz]")
plt.ylabel("Signal Strength [dB]")
plt.tight_layout()
plt.show()

Lo que veas en este punto dependerá de si tu HB100 está encendido y hacia dónde apunta. Si lo sostienes a unos metros del Phaser y lo apuntas hacia el centro, deberías ver algo como esto:

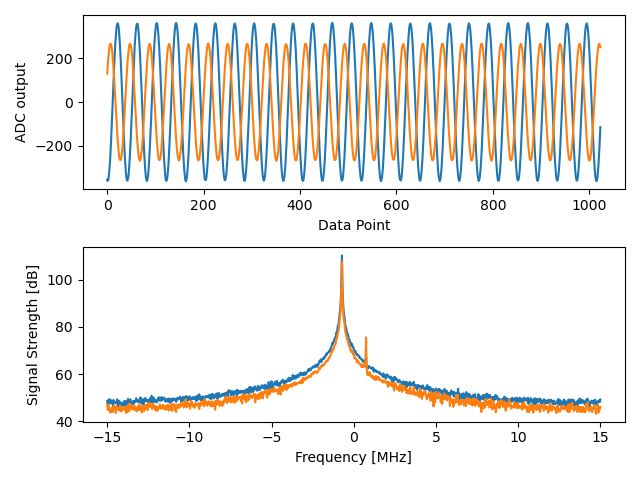
Tenga en cuenta el fuerte pico cerca de 0 Hz, el segundo pico más corto es simplemente un artefacto que puede ignorarse, ya que tiene alrededor de 40 dB menos. El gráfico superior, que muestra el dominio del tiempo, muestra la parte real de los dos canales, por lo que la amplitud relativa entre los dos variará ligeramente dependiendo de dónde sostenga el HB100.

Desempeño Beamforming¶

A continuación, ¡hacemos un barrido en la fase! En el siguiente código barremos la fase de 180 negativos a 180 grados positivos, en un paso de 2 grados. Tenga en cuenta que este no es el ángulo que apunta el formador de haz; es la diferencia de fase entre canales adyacentes. Debemos calcular el ángulo de llegada correspondiente a cada paso de fase, utilizando el conocimiento de la velocidad de la luz, la frecuencia de RF de la señal recibida y el espaciamiento de los elementos del Phaser. La diferencia de fase entre elementos adyacentes viene dada por:

$\phi = \frac{2 \pi d}{\lambda} \sin(\theta_{AOA})$

donde $\theta_{AOA}$ es el ángulo de llegada de la señal con respecto a la orientación frontal, $d$ es el espacio entre antenas en metros y $\lambda$ es la longitud de onda de la señal. Usando la fórmula para la longitud de onda y resolviendo $\theta_{AOA}$ obtenemos:

$\theta_{AOA} = \sin^{-1}\left(\frac{c \phi}{2 \pi f d}\right)$

Veremos esto cuando calculemos steer_angle abajo:

powers = [] # main DOA result
angle_of_arrivals = []
for phase in np.arange(-180, 180, 2): # sweep over angle
    print(phase)
    # set phase difference between the adjacent channels of devices
    for i in range(8):
        channel_phase = (phase * i + phase_cal[i]) % 360.0 # Analog Devices had this forced to be a multiple of phase_step_size (2.8125 or 360/2**6bits) but it doesn't seem nessesary
        phaser.elements.get(i + 1).rx_phase = channel_phase
    phaser.latch_rx_settings() # apply settings

    steer_angle = np.degrees(np.arcsin(max(min(1, (3e8 * np.radians(phase)) / (2 * np.pi * signal_freq * phaser.element_spacing)), -1))) # arcsin argument must be between 1 and -1, or numpy will throw a warning
    # If you're looking at the array side of Phaser (32 squares) then add a *-1 to steer_angle
    angle_of_arrivals.append(steer_angle)
    data = phaser.sdr.rx() # receive a batch of samples
    data_sum = data[0] + data[1] # sum the two subarrays (within each subarray the 4 channels have already been summed)
    power_dB = 10*np.log10(np.sum(np.abs(data_sum)**2))
    powers.append(power_dB)
    # in addition to just taking the power in the signal, we could also do the FFT then grab the value of the max bin, effectively filtering out noise, results came out almost exactly the same in my tests
    #PSD = 10*np.log10(np.abs(np.fft.fft(data_sum * np.blackman(len(data_sum))))**2) # in dB

powers -= np.max(powers) # normalize so max is at 0 dB

plt.plot(angle_of_arrivals, powers, '.-')
plt.xlabel("Angle of Arrival")
plt.ylabel("Magnitude [dB]")
plt.show()

Para cada valor de phase (recuerde, esta es la fase entre elementos adyacentes) configuramos los desfasadores, después de agregar los valores de calibración de fase y forzar que los grados estén entre 0 y 360. Luego tomamos un lote de muestras con rx(), sume los dos canales y luego calcule la potencia en la señal. Luego graficamos la potencia sobre el ángulo de llegada. El resultado debería verse así:

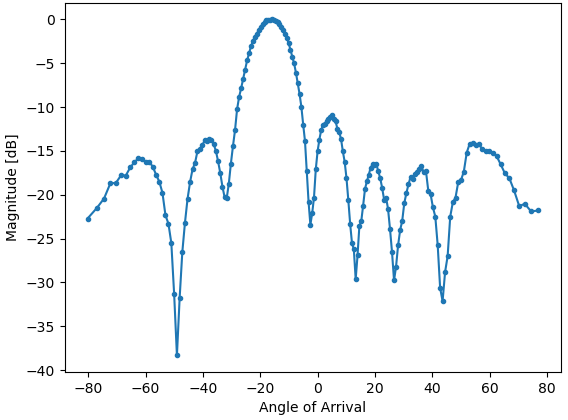
En este ejemplo, el HB100 se mantuvo ligeramente hacia el lado de la mira.

Si desea un gráfico polar, puede utilizar lo siguiente:

# Polar plot
fig, ax = plt.subplots(subplot_kw={'projection': 'polar'})
ax.plot(np.deg2rad(angle_of_arrivals), powers) # x axis in radians
ax.set_rticks([-40, -30, -20, -10, 0])  # Less radial ticks
ax.set_thetamin(np.min(angle_of_arrivals)) # in degrees
ax.set_thetamax(np.max(angle_of_arrivals))
ax.set_theta_direction(-1) # increase clockwise
ax.set_theta_zero_location('N') # make 0 degrees point up
ax.grid(True)
plt.show()

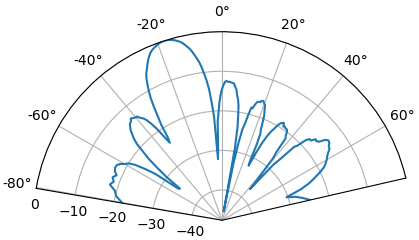
¡Tomando el máximo podemos estimar la dirección de llegada de la señal!

En tiempo real y con reducción espacial¶

Ahora tomemos un momento para hablar sobre la reducción espacial. Hasta ahora hemos dejado los ajustes de ganancia de cada canal en valores iguales, de modo que los ocho canales se sumen equitativamente. Así como aplicamos una ventana antes de tomar una FFT, podemos aplicar una ventana en el dominio espacial aplicando pesos a estos ocho canales. Usaremos exactamente las mismas funciones de ventanas como Hanning, Hamming, etc. También modifiquemos el código para que se ejecute en tiempo real para que sea un poco más divertido:

plt.ion() # needed for real-time view
print("Starting, use control-c to stop")
try:
    while True:
        powers = [] # main DOA result
        angle_of_arrivals = []
        for phase in np.arange(-180, 180, 6): # sweep over angle
            # set phase difference between the adjacent channels of devices
            for i in range(8):
                channel_phase = (phase * i + phase_cal[i]) % 360.0 # Analog Devices had this forced to be a multiple of phase_step_size (2.8125 or 360/2**6bits) but it doesn't seem nessesary
                phaser.elements.get(i + 1).rx_phase = channel_phase

            # set gains, incl the gain_cal, which can be used to apply a taper.  try out each one!
            gain_list = [127] * 8 # rectangular window          [127, 127, 127, 127, 127, 127, 127, 127]
            #gain_list = np.rint(np.hamming(8) * 127)         # [ 10,  32,  82, 121, 121,  82,  32,  10]
            #gain_list = np.rint(np.hanning(10)[1:-1] * 127)  # [ 15,  52,  95, 123, 123,  95,  52,  15]
            #gain_list = np.rint(np.blackman(10)[1:-1] * 127) # [  6,  33,  80, 121, 121,  80,  33,   6]
            #gain_list = np.rint(np.bartlett(10)[1:-1] * 127) # [ 28,  56,  85, 113, 113,  85,  56,  28]
            for i in range(8):
                channel_gain = int(gain_list[i] * gain_cal[i])
                phaser.elements.get(i + 1).rx_gain = channel_gain

            phaser.latch_rx_settings() # apply settings

            steer_angle = np.degrees(np.arcsin(max(min(1, (3e8 * np.radians(phase)) / (2 * np.pi * signal_freq * phaser.element_spacing)), -1))) # arcsin argument must be between 1 and -1, or numpy will throw a warning
            angle_of_arrivals.append(steer_angle)
            data = phaser.sdr.rx() # receive a batch of samples
            data_sum = data[0] + data[1] # sum the two subarrays (within each subarray the 4 channels have already been summed)
            power_dB = 10*np.log10(np.sum(np.abs(data_sum)**2))
            powers.append(power_dB)

        powers -= np.max(powers) # normalize so max is at 0 dB

        # Real-time view
        plt.plot(angle_of_arrivals, powers, '.-')
        plt.xlabel("Angle of Arrival")
        plt.ylabel("Magnitude [dB]")
        plt.draw()
        plt.pause(0.001)
        plt.clf()

except KeyboardInterrupt:
    sys.exit() # quit python

Deberías ver una versión en tiempo real del ejercicio anterior. Intente cambiar qué gain_list se utiliza para jugar con las diferentes ventanas. A continuación se muestra un ejemplo de ventana rectangular (es decir, sin función de ventana):

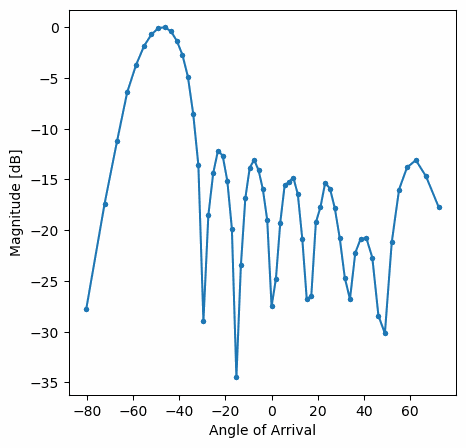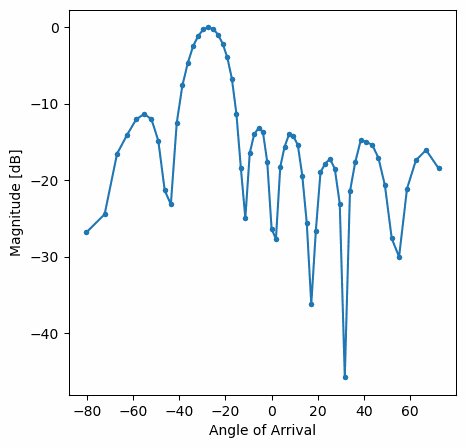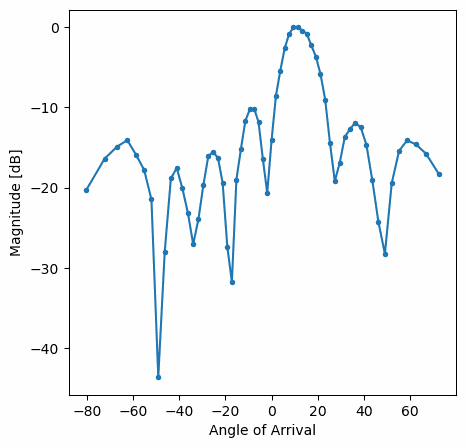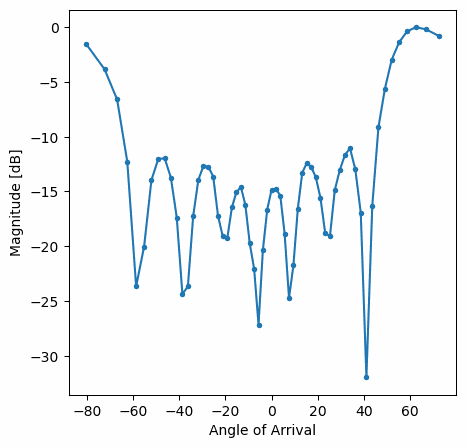
Beamforming animation using the Phaser and a rectangular window

y aquí hay un ejemplo de la ventana Hamming:

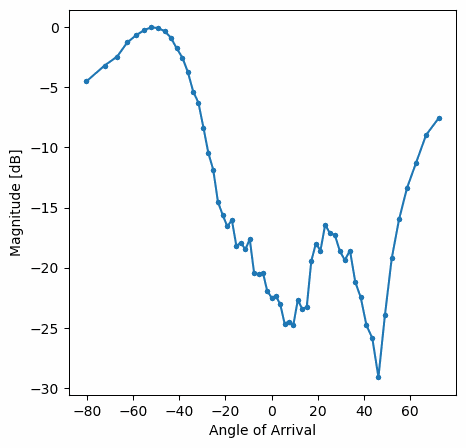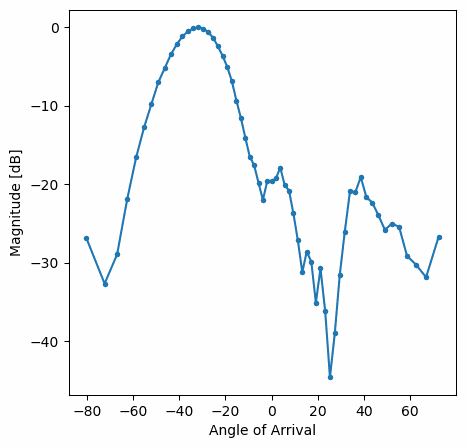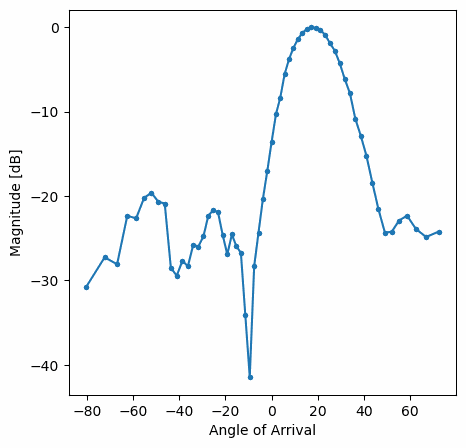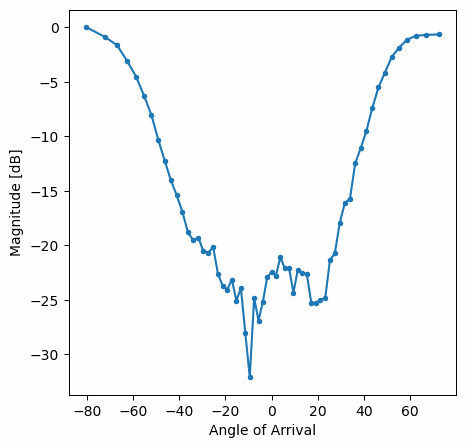
Beamforming animation using the Phaser and a Hamming window

Obsérvese la falta de lóbulos laterales para Hamming. De hecho, todas las ventanas, excepto la rectangular, reducirán en gran medida los lóbulos laterales, pero a cambio el lóbulo principal será un poco más ancho.

Seguimiento monopulso¶

Hasta este punto hemos estado realizando barridos individuales para encontrar el ángulo de llegada de un transmisor de prueba (el HB100). Pero digamos que deseamos recibir continuamente una señal de radar o de comunicaciones, que puede estar en movimiento y provocar que el ángulo de llegada cambie con el tiempo. Nos referimos a este proceso como seguimiento y supone que ya tenemos una estimación aproximada del ángulo de llegada (es decir, el barrido inicial ha identificado una señal de interés). Usaremos el seguimiento monopulso para actualizar de forma adaptativa los pesos a fin de mantener el lóbulo principal apuntando a la señal a lo largo del tiempo, aunque tenga en cuenta que existen otros métodos de seguimiento además del monopulso.

Inventado en 1943 por Robert Page en el Laboratorio de Investigación Naval (NRL), el concepto básico del seguimiento monopulso es utilizar dos haces, ambos ligeramente desviados del ángulo de llegada actual (o al menos nuestra estimación del mismo), pero en lados diferentes como se muestra en el siguiente diagrama.

Monopulse beam diagram showing two beams and the sum beam

Luego tomamos la suma y la diferencia (también conocida como delta) de estos dos haces digitales, lo que significa que debemos usar dos canales digitales del Phaser, lo que hace que este sea un enfoque de matriz híbrida (aunque ciertamente se podría hacer la suma y la diferencia en analógico con dispositivos de hardware personalizados). El haz suma equivaldrá a un haz centrado en el ángulo actual de llegada estimado, como se muestra arriba, lo que significa que este haz se puede utilizar para demodular/decodificar la señal de interés. El haz delta, como lo llamaremos, es más difícil de visualizar, pero tendrá una estimación nula en el ángulo de llegada. Podemos usar la relación entre el haz suma y el haz delta (denominado error) para realizar nuestro seguimiento. Este proceso se explica mejor con un breve fragmento de Python; Recuerde que la función rx() devuelve un lote de muestras de ambos canales, por lo que en el siguiente código data[0] es el primer canal del Pluto (primer conjunto de cuatro elementos del Phaser) y data[1] es el segundo canal (segundo conjunto de cuatro elementos). Para crear dos direcciones, para cada uno de los dos conjuntos por separado. Podemos calcular la suma, delta y error de la siguiente manera:

data = phaser.sdr.rx()
sum_beam = data[0] + data[1]
delta_beam = data[0] - data[1]
error = np.mean(np.real(delta_beam / sum_beam))

El signo del error nos dice de qué dirección proviene realmente la señal y la magnitud nos dice a qué distancia estamos de la señal. Luego podemos usar esta información para actualizar la estimación del ángulo de llegada y los pesos. Repitiendo este proceso en tiempo real podemos rastrear la señal.

Ahora, saltando al ejemplo completo de Python, comenzaremos copiando el código que usamos anteriormente para realizar un barrido de 180 grados. El único código que agregaremos es sacar la fase en la que la potencia recibida era máxima:

# Sweep phase once to get initial estimate for AOA, using code above
# ...
current_phase = phase_angles[np.argmax(powers)]
print("max_phase:", current_phase)

A continuación crearemos dos haces, comenzaremos probando 5 grados más bajos y 5 grados más altos que la estimación actual, aunque tenga en cuenta que esto está en unidades de fase, no los hemos convertido a ángulo de dirección, aunque son similares. El siguiente código es esencialmente dos copias del código que usamos anteriormente para configurar los desfasadores de cada canal, excepto que usamos los primeros 4 elementos para el haz inferior y los últimos 4 elementos para el haz superior:

# Now we create the two beams on either side of our current estimate
phase_offset = np.radians(5) # TRY TWEAKING THIS - specify offset from center in degrees
phase_lower = current_phase - phase_offset
phase_upper = current_phase + phase_offset
# first 4 elements will be used for lower beam
for i in range(0, 4):
   channel_phase = (phase_lower * i + phase_cal[i]) % 360.0
   phaser.elements.get(i + 1).rx_phase = channel_phase
# last 4 elements will be used for upper beam
for i in range(4, 8):
   channel_phase = (phase_upper * i + phase_cal[i]) % 360.0
   phaser.elements.get(i + 1).rx_phase = channel_phase
phaser.latch_rx_settings() # apply settings

Antes de realizar el seguimiento real, probemos lo anterior manteniendo constantes los pesos del haz y moviendo el HB100 hacia la izquierda y hacia la derecha (después de que termine de inicializarse para encontrar el ángulo inicial):

print("START MOVING THE HB100 A LITTLE LEFT AND RIGHT")
error_log = []
for i in range(1000):
   data = phaser.sdr.rx() # receive a batch of samples
   sum_beam = data[0] + data[1]
   delta_beam = data[0] - data[1]
   error = np.mean(np.real(delta_beam / sum_beam))
   error_log.append(error)
   print(error)
   time.sleep(0.01)

plt.plot(error_log)
plt.plot([0,len(error_log)], [0,0], 'r--')
plt.xlabel("Time")
plt.ylabel("Error")
plt.show()

Showing error function for monopulse tracking without actually updating the weights

Lo que sucede en este ejemplo es que estoy moviendo el HB100. Empiezo manteniéndolo en una posición estable mientras se realiza el barrido de 180 grados, luego, una vez hecho, lo muevo un poco hacia la derecha y lo muevo, luego lo muevo hacia la izquierda de donde comencé y lo muevo. Luego, alrededor del tiempo = 400 en la trama, lo muevo hacia el otro lado y lo mantengo allí por un momento, antes de agitarlo una vez más. La conclusión es que cuanto más se aleja el HB100 del ángulo inicial, mayor es el error, y el signo del error nos indica de qué lado está el HB100 en relación con el ángulo inicial.

Ahora usemos el valor de error para actualizar los pesos. Nos desharemos del bucle for anterior y crearemos un nuevo bucle for durante todo el proceso. Para mayor claridad, tenemos el ejemplo de código completo a continuación, excepto la parte inicial donde hicimos el barrido de 180 grados:

# Sweep phase once to get initial estimate for AOA
# ...
current_phase = phase_angles[np.argmax(powers)]
print("max_phase:", current_phase)

# Now we'll actually update the current_phase based on the error
print("START MOVING THE HB100 A LITTLE LEFT AND RIGHT")
phase_log = []
error_log = []
for ii in range(500):
   # Now we create the two beams on either side of our current estimate, using the specified offset
   phase_offset = np.radians(5)
   phase_lower = current_phase - phase_offset
   phase_upper = current_phase + phase_offset
   # first 4 elements will be used for lower beam
   for i in range(0, 4):
         channel_phase = (phase_lower * i + phase_cal[i]) % 360.0
         phaser.elements.get(i + 1).rx_phase = channel_phase
   # last 4 elements will be used for upper beam
   for i in range(4, 8):
         channel_phase = (phase_upper * i + phase_cal[i]) % 360.0
         phaser.elements.get(i + 1).rx_phase = channel_phase
   phaser.latch_rx_settings() # apply settings

   data = phaser.sdr.rx() # receive a batch of samples
   sum_beam = data[0] + data[1]
   delta_beam = data[0] - data[1]
   error = np.mean(np.real(delta_beam / sum_beam))
   error_log.append(error)
   print(error)

   # Update our estimated angle of arrival based on error
   current_phase += -10 * error # was manually tweaked until it seemed to track at a nice speed
   steer_angle = np.degrees(np.arcsin(max(min(1, (3e8 * np.radians(current_phase)) / (2 * np.pi * signal_freq * phaser.element_spacing)), -1)))
   phase_log.append(steer_angle) # looks nicer to plot steer angle instead of straight phase

   time.sleep(0.01)

fig, [ax0, ax1] = plt.subplots(2, 1, figsize=(8, 10))

ax0.plot(phase_log)
ax0.plot([0,len(phase_log)], [0,0], 'r--')
ax0.set_xlabel("Time")
ax0.set_ylabel("Phase Estimate [degrees]")

ax1.plot(error_log)
ax1.plot([0,len(error_log)], [0,0], 'r--')
ax1.set_xlabel("Time")
ax1.set_ylabel("Error")

plt.show()

Monopulse tracking demo using a Phaser and HB100 being waved around infront of it

Puede ver que el error es esencialmente la derivada de la estimación de fase; debido a que estamos realizando un seguimiento exitoso, la estimación de fase es más o menos el ángulo de llegada real. No está claro mirando sólo estos gráficos, pero cuando hay un movimiento repentino, al sistema le toma una pequeña fracción de segundo ajustarse y ponerse al día. El objetivo es que el cambio de ángulo de llegada nunca sea tan rápido como para que la señal llegue más allá de los lóbulos principales de los dos haces.

Es mucho más fácil visualizar el proceso cuando la matriz es solo 1D, pero los casos de uso prácticos de seguimiento monopulso casi siempre son 2D (usando una matriz 2D/planar en lugar de una matriz lineal como el Phaser). Para el caso 2D, se crean cuatro direcciones en lugar de dos, y después del proceso hay una dirección de suma única y cuatro direcciones delta que se utilizan para dirigir en ambas dimensiones.

Radar con Phaser¶

Proximamente!

Conclusiones¶

El código completo utilizado para generar las figuras de este capítulo está disponible en la página GitHub del libro de texto.