21. 2D формування променя¶
Цей розділ розширює матеріал про 1D формування променя/визначення напрямку приходу (DOA) на двовимірні решітки. Ми почнемо з простої прямокутної решітки та виведемо рівняння вектора наведення й формувач променя MVDR, після чого попрацюємо з реальними даними з решітки 3x5. Наостанок скористаємося інтерактивним інструментом, щоб дослідити вплив різних геометрій решіток і відстаней між елементами.
Прямокутні решітки та 2D формування променя¶
Прямокутні решітки (відомі також як планарні решітки) складаються з двовимірного масиву елементів. Додатковий вимір додає трохи складності, але діють ті ж базові принципи, і найважчою частиною стане візуалізація результатів (наприклад, простих полярних графіків уже не буде, нам знадобляться 3D-поверхні). Хоч наша решітка тепер 2D, це не означає, що ми повинні додавати вимір до кожної структури даних, з якою працювали. Наприклад, вагові коефіцієнти ми й далі зберігатимемо як 1D масив комплексних чисел. Втім, позиції елементів нам доведеться представити у 2D. Ми й надалі використовуватимемо theta для позначення азимутального кута, але введемо новий кут — phi, тобто кут місця. Існує багато конвенцій сферичних координат, але ми використовуватимемо таку:
Що відповідає співвідношенням:
Ми також перейдемо до узагальненого рівняння вектора наведення, яке не прив’язане до конкретної геометрії решітки:
де \(\boldsymbol{p}\) — набір координат x/y/z елементів у метрах (розмір Nr x 3), а \(u\) — напрямок, у який ми хочемо спрямувати решітку, представлений одиничним вектором у координатах x/y/z (розмір 3x1). У Python це виглядає так:
def steering_vector(pos, dir):
# Nrx3 3x1
return np.exp(2j * np.pi * pos @ dir / wavelength) # виводить вектор Nr x 1 (стовпчик)
Спробуймо використати це узагальнене рівняння вектора наведення для простої лінійної решітки (ULA) з чотирма елементами, щоб пов’язати його з тим, що ми вже вивчали. Тепер ми представлятимемо d у метрах, а не відносно довжини хвилі. Розмістимо елементи вздовж осі y:
Nr = 4
fc = 5e9
wavelength = 3e8 / fc
d = 0.5 * wavelength # у метрах
# Зберігатимемо позиції елементів у списку координат (x, y, z), навіть якщо це просто ULA вздовж осі y
pos = np.zeros((Nr, 3)) # Позиції елементів як список координат x, y, z у метрах
for i in range(Nr):
pos[i,0] = 0 # координата x
pos[i,1] = d * i # координата y
pos[i,2] = 0 # координата z
Наступна ілюстрація показує вигляд ULA зверху з прикладом кута θ у 20 градусів.
Залишилося лише пов’язати нашу стару theta з новим підходом через одиничний вектор. Ми можемо досить просто обчислити dir на основі theta: знаємо, що компоненти x і z нашого одиничного вектора дорівнюватимуть 0, адже ми все ще в одномірному просторі, а згідно з нашою конвенцією сферичних координат компонент y дорівнюватиме np.cos(theta), тобто повний код виглядає як dir = np.asmatrix([0, np.cos(theta_i), 0]).T. На цьому етапі ви маєте змогу пов’язати наше узагальнене рівняння вектора наведення з рівнянням вектора наведення для ULA, яке ми використовували раніше. Спробуйте цей новий код, виберіть theta між 0 і 360 градусами (не забудьте перевести в радіани!), і вектор наведення повинен мати розмір 4x1.
Тепер перейдемо до 2D-випадку. Розмістимо нашу решітку в площині X-Z з осьовою лінією, спрямованою горизонтально вздовж додатного напрямку осі y (\(\theta = 0\), \(\phi = 0\)). Використаємо той самий крок між елементами, але тепер матимемо загалом 16 елементів:
# Тепер перейдемо до 2D, використовуючи решітку 4x4 з інтервалом у півдовжини хвилі, тобто 16 елементів
Nr = 16
# Позиції елементів як список координат x, y, z у метрах, розміщуємо решітку в площині X-Z
pos = np.zeros((Nr,3))
for i in range(Nr):
pos[i,0] = d * (i % 4) # координата x
pos[i,1] = 0 # координата y
pos[i,2] = d * (i // 4) # координата z
Вигляд зверху нашої прямокутної решітки 4x4:
Щоб спрямуватися на певні θ та φ, нам потрібно перетворити ці кути на одиничний вектор. Ми можемо використати те саме узагальнене рівняння вектора наведення, але тепер мусимо обчислити одиничний вектор на основі обох кутів, використовуючи формули з початку цього розділу:
# Спрямуймося у довільному напрямку
theta = np.deg2rad(60) # азимутальний кут
phi = np.deg2rad(30) # кут місця
# Використовуючи нашу конвенцію сферичних координат, можемо обчислити одиничний вектор:
def get_unit_vector(theta, phi): # кути в радіанах
return np.asmatrix([np.sin(theta) * np.cos(phi), # компонент x
np.cos(theta) * np.cos(phi), # компонент y
np.sin(phi)]).T # компонент z
dir = get_unit_vector(theta, phi)
# dir має розмір 3x1
# [[0.75 ]
# [0.4330127]
# [0.5 ]]
Тепер скористаймося нашою функцією узагальненого вектора наведення, щоб обчислити сам вектор наведення:
s = steering_vector(pos, dir)
# Застосуємо звичайний формувач променя, у якому ваги дорівнюють вектору наведення, та побудуємо діаграму спрямованості
w = s # вектор ваг 16x1
На цьому етапі варто зазначити, що ми не змінювали розмірності даних, переходячи з 1D у 2D: ми просто отримали ненульові компоненти x/y/z, рівняння вектора наведення лишилося таким самим, а ваги — все ще 1D масивом. Може виникнути спокуса сформувати ваги у вигляді 2D масиву, щоб візуально відповідати геометрії решітки, але в цьому немає потреби — краще залишити їх 1D. Для кожного елемента існує відповідна вага, і список ваг має той самий порядок, що й список позицій елементів.
Візуалізувати діаграму спрямованості для цих ваг трохи складніше, бо нам потрібен 3D-графік або 2D-теплокарта. Ми проскануємо theta та phi, щоб отримати 2D масив рівнів потужності, а потім побудуємо його за допомогою imshow(). Наведений нижче код саме це й робить, а результат показано на рисунку нижче, разом із точкою в раніше заданому куті:
resolution = 100 # кількість точок у кожному напрямку
theta_scan = np.linspace(-np.pi/2, np.pi/2, resolution) # азимутальні кути
phi_scan = np.linspace(-np.pi/4, np.pi/4, resolution) # кути місця
results = np.zeros((resolution, resolution)) # 2D масив для зберігання результатів
for i, theta_i in enumerate(theta_scan):
for j, phi_i in enumerate(phi_scan):
a = steering_vector(pos, get_unit_vector(theta_i, phi_i)) # фактор решітки
results[i, j] = np.abs(w.conj().T @ a)[0,0] # потужність сигналу, лінійний масштаб виглядає краще
plt.imshow(results.T, extent=(theta_scan[0]*180/np.pi, theta_scan[-1]*180/np.pi, phi_scan[0]*180/np.pi, phi_scan[-1]*180/np.pi), origin='lower', aspect='auto', cmap='viridis')
plt.colorbar(label='Потужність [лінійна]')
plt.scatter(theta*180/np.pi, phi*180/np.pi, color='red', s=50) # Додаємо точку в правильному θ/φ
plt.xlabel('Азимутальний кут [градуси]')
plt.ylabel('Кут місця [градуси]')
plt.show()
Змоделюймо тепер реальні відліки; додамо два перешкодні тони, що приходять з різних напрямків:
N = 10000 # кількість відліків для симуляції
jammer1_theta = np.deg2rad(-30)
jammer1_phi = np.deg2rad(10)
jammer1_dir = get_unit_vector(jammer1_theta, jammer1_phi)
jammer1_s = steering_vector(pos, jammer1_dir) # Nr x 1
jammer1_tone = np.exp(2j*np.pi*0.1*np.arange(N)).reshape(1,-1) # формуємо рядок
jammer2_theta = np.deg2rad(10)
jammer2_phi = np.deg2rad(50)
jammer2_dir = get_unit_vector(jammer2_theta, jammer2_phi)
jammer2_s = steering_vector(pos, jammer2_dir)
jammer2_tone = np.exp(2j*np.pi*0.2*np.arange(N)).reshape(1,-1) # формуємо рядок
noise = np.random.normal(0, 1, (Nr, N)) + 1j * np.random.normal(0, 1, (Nr, N)) # комплексний гаусів шум
r = jammer1_s @ jammer1_tone + jammer2_s @ jammer2_tone + noise # отримуємо матрицю відліків 16 x 10000
Просто для цікавості обчислимо ваги формувача променя MVDR у напрямку тих самих θ та φ, які ми використовували раніше (одиничний вектор цього напрямку все ще збережено в dir):
s = steering_vector(pos, dir) # 16 x 1
R = np.cov(r) # коваріаційна матриця 16 x 16
Rinv = np.linalg.pinv(R)
w = (Rinv @ s)/(s.conj().T @ Rinv @ s) # рівняння MVDR/Капона
Замість того щоб дивитися на діаграму спрямованості у незручному 3D-графіку, скористаймося альтернативним способом перевірити адекватність цих ваг: оцінимо відгук ваг у різних напрямках і розрахуємо потужність у дБ. Почнімо з напрямку, куди ми спрямовувалися:
# Потужність у напрямку наведення (theta=60, phi=30, цей напрямок і досі збережено в dir):
a = steering_vector(pos, dir) # фактор решітки
resp = w.conj().T @ a # скаляр
print("Power in direction we are pointing:", 10*np.log10(np.abs(resp)[0,0]), 'dB')
Це виводить 0 дБ, що й очікувано, адже мета MVDR — забезпечити одиничну потужність у бажаному напрямку. Тепер перевірмо потужність у напрямках двох глушників, а також у випадковому напрямку та в напрямку, що відхиляється на один градус від бажаного (код той самий, просто оновлюйте dir). Результати показано в таблиці нижче:
| Напрямок | Підсилення |
|---|---|
dir (напрямок, використаний для пошуку ваг MVDR) |
0 дБ |
| Глушник 1 | -17.488 дБ |
| Глушник 2 | -18.551 дБ |
Відхилення на 1 градус від dir і за \(\theta\), і за \(\phi\) |
-0.00683 дБ |
| Випадковий напрямок | -10.591 дБ |
Ваші результати можуть відрізнятися через випадковий шум, що використовується для формування прийнятих відліків і, відповідно, для обчислення R. Але головний висновок у тому, що глушники потраплять у нуль і матимуть дуже низьку потужність, напрямок, зміщений на один градус від dir, буде трохи нижче 0 дБ, але все ще в головній пелюстці, а випадковий напрямок буде нижче 0 дБ, але вищий за глушники і дуже різний у кожному запуску симуляції. Зверніть увагу, що з MVDR ви отримуєте підсилення 0 дБ у головній пелюстці, тоді як зі звичайним формувачем променя ви отримали б \(10 \log_{10}(Nr)\), тобто близько 12 дБ для нашої 16-елементної решітки, що демонструє одну з особливостей MVDR.
Код для цього розділу можна знайти тут.
Обробка сигналів із реальної 2D решітки¶
У цій секції ми працюємо з реальними даними, записаними з решітки 3x5, створеної на основі платформи QUAD-MxFE від Analog Devices, яка підтримує до 16 каналів передавання та приймання (ми використали лише 15 і тільки в режимі приймача). Нижче наведено два записи: перший містить один випромінювач, розташований на осьовій лінії решітки, і використовується для калібрування. Другий запис містить два випромінювачі в різних напрямках, які ми використаємо для формування променя та тестування DOA.
- IQ-запис лише випромінювача C (використовується для калібрування, оскільки C розташовано на осьовій лінії)
- IQ-запис випромінювачів B і D (використовується для формування променя/DOA)
QUAD-MxFE було налаштовано на 2.8 ГГц, а всі передавачі використовували простий тон у межах смуги спостереження. Цікаво, що для цієї DSP частота дискретизації насправді неважлива: жодна з методик обробки решітки, які ми застосовуємо, не залежить від частоти дискретизації, вони лише припускають, що сигнал перебуває десь у сигналі базової смуги. DSP залежить від центральної частоти, адже фазовий зсув між елементами залежить від частоти й кута приходу. Це протилежно більшості інших видів обробки сигналів, де частота дискретизації важлива, а центральна — ні.
Ми можемо завантажити ці записи в Python за допомогою такого коду:
import numpy as np
import matplotlib.pyplot as plt
r = np.load("DandB_capture1.npy")[0:15] # 16-й елемент не підключено, але його все одно записали
r_cal = np.load("C_only_capture1.npy")[0:15] # лише калібрувальний сигнал (на осьовій лінії)
Відстань між антенами становила 0.051 метра. Ми можемо представити позиції елементів як список координат x, y, z у метрах. Розмістимо решітку в площині X-Z, оскільки її було змонтовано вертикально (з осьовою лінією, спрямованою горизонтально).
fc = 2.8e9 # центральна частота в Гц
d = 0.051 # відстань між антенами в метрах
wavelength = 3e8 / fc
Nr = 15
rows = 3
cols = 5
# Позиції елементів як список координат x, y, z у метрах
pos = np.zeros((Nr, 3))
for i in range(Nr):
pos[i,0] = d * (i % cols) # координата x
pos[i,1] = 0 # координата y
pos[i,2] = d * (i // cols) # координата z
# Побудуємо та підпишемо позиції елементів
fig = plt.figure()
ax = fig.add_subplot(projection='3d')
ax.scatter(pos[:,0], pos[:,1], pos[:,2], 'o')
# Підписи індексів
for i in range(Nr):
ax.text(pos[i,0], pos[i,1], pos[i,2], str(i), fontsize=10)
plt.xlabel("Позиція X [м]")
plt.ylabel("Позиція Y [м]")
ax.set_zlabel("Позиція Z [м]")
plt.grid()
plt.show()
На графіку кожен елемент позначений власним індексом, який відповідає порядку елементів у IQ-відліках r та r_cal.
Калібрування виконується, використовуючи лише відліки r_cal, які були записані з увімкненим передавачем на осьовій лінії. Мета — знайти фазові та амплітудні зсуви для кожного елемента. За ідеального калібрування і за умови, що передавач точно на осьовій лінії, усі окремі приймальні елементи мають отримувати однаковий сигнал, синфазний і з однаковою амплітудою. Але через недоліки решітки/кабелів/антен кожен елемент матиме власні фазовий та амплітудний зсуви. Процес калібрування полягає у знаходженні цих зсувів, які ми згодом застосуємо до відліків r перед будь-якою обробкою решітки.
Існує багато способів калібрування, але ми використаємо метод, що передбачає власне розкладання коваріаційної матриці. Коваріаційна матриця — це квадратна матриця розміру Nr x Nr, де Nr — кількість приймальних елементів. Власний вектор, що відповідає найбільшому власному значенню, представляє отриманий сигнал (сподіваємося), і ми використаємо його для пошуку фазових зсувів кожного елемента, просто взявши фазу кожного елементу власного вектора і нормалізувавши її за першим елементом, який ми вважатимемо еталонним. Амплітудне калібрування не використовує власний вектор, а натомість використовує середню амплітуду отриманого сигналу для кожного елементу.
# Обчислюємо коваріаційну матрицю, вона має розмір Nr x Nr
R_cal = r_cal @ r_cal.conj().T
# власне розкладання, v[:,i] — власний вектор, що відповідає власному значенню w[i]
w, v = np.linalg.eig(R_cal)
# Побудуємо власні значення, щоб переконатися, що одне з них значно більше за інші
w_dB = 10*np.log10(np.abs(w))
w_dB -= np.max(w_dB) # нормалізація
fig, (ax1) = plt.subplots(1, 1, figsize=(7, 3))
ax1.plot(w_dB, '.-')
ax1.set_xlabel('Індекс')
ax1.set_ylabel('Власне значення [дБ]')
plt.show()
# Використовуємо максимальний власний вектор для калібрування
v_max = v[:, np.argmax(np.abs(w))]
mags = np.mean(np.abs(r_cal), axis=1)
mags = mags[0] / mags # нормалізуємо відносно першого елемента
phases = np.angle(v_max)
phases = phases[0] - phases # нормалізуємо відносно першого елемента
cal_table = mags * np.exp(1j * phases)
print("cal_table", cal_table)
На рисунку нижче показано розподіл власних значень; ми хочемо переконатися, що є лише одне велике значення, а решта малі, що відповідає одному прийнятому сигналу. Будь-які завади або багатопроменевість погіршуватимуть процес калібрування.
Таблиця калібрування — це список комплексних чисел, по одному для кожного елемента, що представляють фазові та амплітудні зсуви (їх простіше подавати у прямокутній формі, а не в полярній). Перший елемент — еталонний і завжди дорівнює 1.0 + 0.j. Решта елементів — це зсуви для кожного елемента у тому ж порядку, який ми використали для pos.
[1. +0.j 0.99526771+0.76149029j -0.91754588-0.66825262j
-0.96840297+0.37251012j 0.87866849+0.40446665j 0.56040169+1.50499875j
-0.80109196-1.29299264j -1.28464742-0.31133052j 1.26622038+0.46047599j
2.01855809+9.77121302j -0.29249322-1.09413205j -1.0372309 -0.17983522j
-0.70614339+0.78682873j -0.75612972+5.67234809j 1.00032754-0.60824109j]
Ми можемо застосувати ці зсуви до будь-якого набору відліків, записаних решіткою, просто перемноживши кожен елемент відліків на відповідний елемент таблиці калібрування:
# Застосовуємо калібрувальні зсуви до r
for i in range(Nr):
r[i, :] *= cal_table[i]
Як невеличкий відступ, саме тому ми обчислювали зсуви у вигляді mags[0] / mags та phases[0] - phases: якби ми зробили навпаки, то довелося б ділити значення під час застосування, а нам зручніше множити.
Далі виконаємо оцінювання DOA за допомогою алгоритму MUSIC. Ми використаємо функції steering_vector() та get_unit_vector(), визначені раніше, щоб обчислити вектор наведення для кожного елемента решітки, а потім застосуємо MUSIC для оцінки напрямку приходу двох випромінювачів у відліках r. Алгоритм MUSIC розглядався в попередньому розділі.
# DOA з використанням MUSIC
resolution = 400 # кількість точок у кожному напрямку
theta_scan = np.linspace(-np.pi/2, np.pi/2, resolution) # азимутальні кути
phi_scan = np.linspace(-np.pi/4, np.pi/4, resolution) # кути місця
results = np.zeros((resolution, resolution)) # 2D масив для результатів
R = np.cov(r) # коваріаційна матриця 15 x 15
Rinv = np.linalg.pinv(R)
expected_num_signals = 4
w, v = np.linalg.eig(R) # власне розкладання, v[:,i] — власний вектор для w[i]
eig_val_order = np.argsort(np.abs(w))
v = v[:, eig_val_order] # сортуємо власні вектори у цьому порядку
V = np.zeros((Nr, Nr - expected_num_signals), dtype=np.complex64) # шумовий підпростір — решта власних значень
for i in range(Nr - expected_num_signals):
V[:, i] = v[:, i]
for i, theta_i in enumerate(theta_scan):
for j, phi_i in enumerate(phi_scan):
dir_i = get_unit_vector(-1*theta_i, phi_i) # TODO з’ясувати, чому потрібний множник -1, щоб збігалося з реальністю
s = steering_vector(pos, dir_i) # 15 x 1
music_metric = 1 / (s.conj().T @ V @ V.conj().T @ s)
music_metric = np.abs(music_metric).squeeze()
music_metric = np.clip(music_metric, 0, 2) # Корисно для варіанта ABCD
results[i, j] = music_metric
Наші результати двовимірні, адже решітка теж 2D, тому нам доведеться використати або 3D-графік, або 2D-теплокарту. Спробуймо обидва. Спочатку побудуємо 3D-графік, де на одній осі буде кут місця, а на іншій — азимут:
# 3D-графік DOA у координатах азимут/кут місця
results = 10*np.log10(results) # переводимо в дБ
results[results < -20] = -20 # обрізаємо вісь z на певному рівні дБ
fig, ax = plt.subplots(subplot_kw={"projection": "3d", "computed_zorder": False})
surf = ax.plot_surface(np.rad2deg(theta_scan[:,None]), # type: ignore
np.rad2deg(phi_scan[None,:]),
results,
cmap='viridis')
#ax.set_zlim(-10, results[max_idx])
ax.set_xlabel('Азимут (theta)')
ax.set_ylabel('Кут місця (phi)')
ax.set_zlabel('Потужність [дБ]') # type: ignore
fig.savefig('../_images/2d_array_3d_doa_plot.svg', bbox_inches='tight')
plt.show()
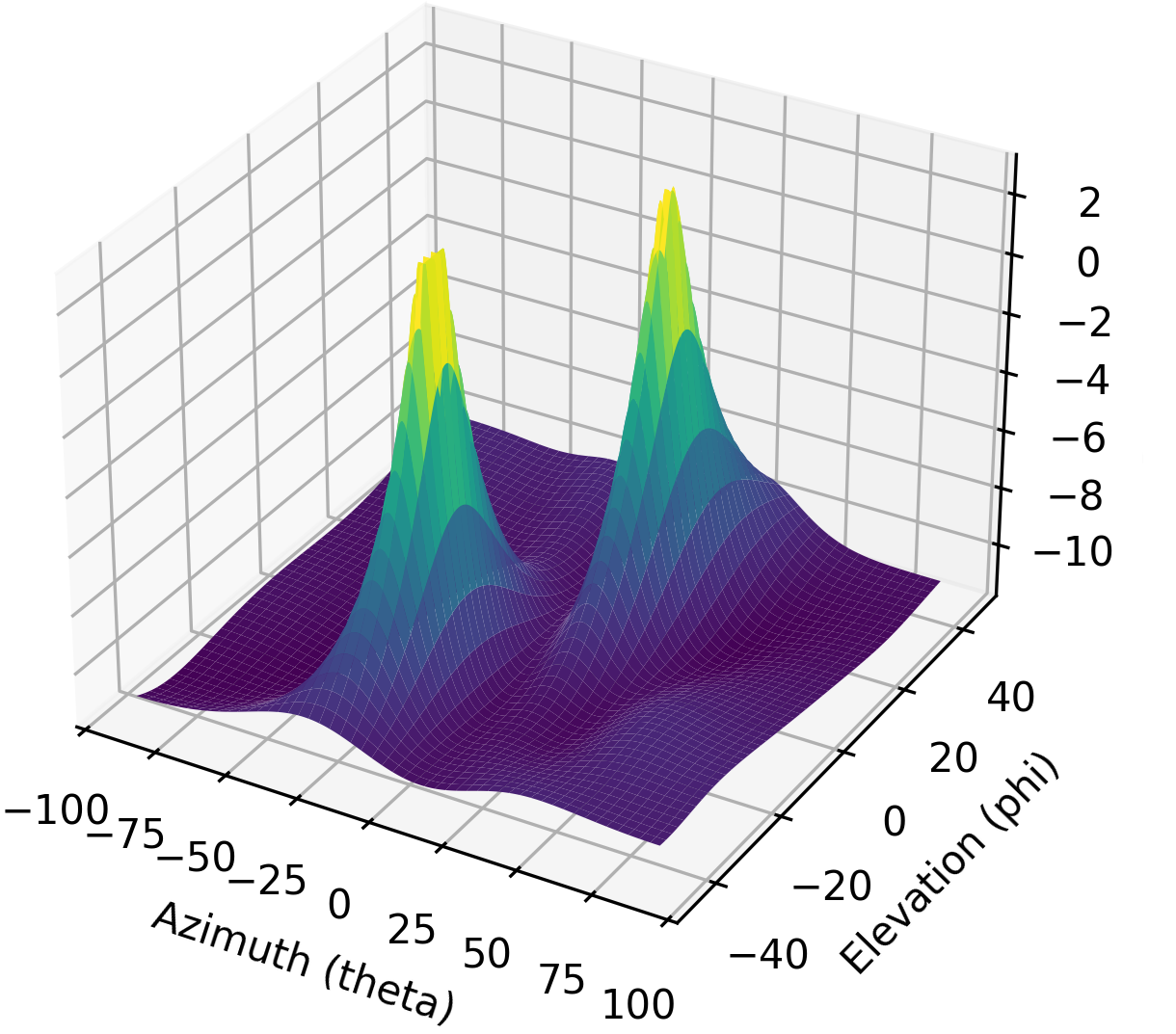
Залежно від ситуації читати значення з 3D-графіка може бути незручно, тож можемо також побудувати 2D-теплокарту за допомогою imshow():
# 2D-теплокарта азимут/кут місця (аналогічно до попереднього, але в 2D)
extent=(np.min(theta_scan)*180/np.pi,
np.max(theta_scan)*180/np.pi,
np.min(phi_scan)*180/np.pi,
np.max(phi_scan)*180/np.pi)
plt.imshow(results.T, extent=extent, origin='lower', aspect='auto', cmap='viridis') # type: ignore
plt.colorbar(label='Потужність [лінійна]')
plt.xlabel('Theta (азимут, градуси)')
plt.ylabel('Phi (кут місця, градуси)')
plt.savefig('../_images/2d_array_2d_doa_plot.svg', bbox_inches='tight')
plt.show()
З цієї 2D-карти ми легко можемо зчитати оцінені азимут і кут місця двох випромінювачів (і переконатися, що їх було лише два). Відповідно до випробувальної установки, яка використовувалася для цього запису, результати відповідають реальності, хоча точні азимут і кут місця випромінювачів не вимірювалися, адже для цього потрібне спеціалізоване обладнання.
Як вправу, спробуйте застосувати звичайний формувач променя, а також MVDR, і порівняйте результати з MUSIC.
Повний код цієї частини можна знайти тут.
Інтерактивний інструмент¶
Наступний інтерактивний інструмент створив Джейсон Дербін, інженер із фазованих решіток-фрилансер, який люб’язно дозволив вбудувати його в PySDR; ви можете відвідати повну версію проєкту або його консалтинговий бізнес. Цей інструмент дозволяє змінювати геометрію фазованої решітки, крок між елементами, напрямок наведення, додавати аподизацію бічних пелюсток та інші можливості.
Декілька деталей про інструмент: антенні елементи вважаються ізотропними. Однак під час розрахунку направленості припускається випромінювання в напівсферу (тобто без задніх пелюсток). Тому обчислена направленість буде на 3 дБі вищою, ніж для ідеально ізотропних елементів (іншими словами, посилення окремого елемента становить +3.0 дБі). Сітку можна зробити щільнішою, збільшуючи кількість точок для theta/phi, u/v або азимуту/куту місця. Натискання (або довге натискання) на елементи графіків фази/атенюації дозволяє вручну встановлювати фазу/атенюацію («не забудьте увімкнути режим перевизначення»). Крім того, у вікні атенюації можна вимкнути окремі елементи. Наведення курсора (або торкання) 2D-графіка далекого поля чи графіків геометрії показує значення у точці під курсором.
